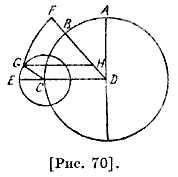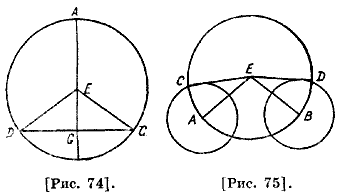Аль-Фараби

КОММЕНТАРИИ К "АЛЬМАГЕСТУ" ПТОЛЕМЕЯ

* О наблюдениях, которые следует использовать для познания движения Луны * Об определении времени оборотов Луны * О частных и равномерных движениях Луны * О том, что Луна имеет одно и то же неравенство как относительно эксцентрического круга, так и относительно эпицикла * Об определении первого и простого неравенства Луны * Об исправлении равномерных движений Луны по долготе и аномалии * Об эпохе равномерных движений Луны по долготе и аномалии * Об исправлении движений Луны по широте и об их эпохе * О том, что принятая Гиппархом разница величины [лунного] неравенства получается не из-за принципов, по которым он действовал, а вследствие вычисления * Примечания *

ЧЕТВЕРТАЯ КНИГА¹²⁴

О наблюдениях, которые следует использовать для познания движения Луны

После изложения вопроса о Солнце Птолемей в первую очередь рассмотрел вопрос о Луне. Наблюдать за Солнцем легче, чем за Луной, так как тело Земли не имеет ощутимой величины относительно орбиты Солнца и наблюдение, произведенное с поверхности Земли, не отличается значительно от «истинного наблюдения» из центра Земли, если бы можно было его произвести. Это различие называется параллаксом, который представляет собой дугу эклиптики, ограниченной концами двух линий, одна из них проведена из глаза, а другая — из центра Земли, причем они встречаются в центре светила, а затем расходятся после него и идут до эклиптики. Так как Луна ближе к Земле, она имеет параллакс ощутимой величины. Только в зените эти две линии, проведенные из глаза и из центра Земли, совпадают. Следовательно, с самого начала при нахождении истинного положения Луны и выяснении общих вопросов следует полагаться не на инструменты наблюдения, а на лунные затмения: лунные затмения отличаются от солнечных, происходящих в зависимости от положения наблюдателей и изменяющихся с изменением [места] наблюдения, так как затмения [Солнца происходят], когда Луна находится между глазом и Солнцем; лунные же затмения представляют собой исчезновение света Солнца с тела Луны из-за преграждения его Землей. Это происходит с самой Луной и не зависит от наблюдателя¹²⁵.

[Истина] Солнца может быть установлена в любое время, которое мы пожелаем. Но когда Луна находится в середине затмения, она диаметрально противоположна Солнцу. Поэтому мы можем определить истинное положение Луны в середине затмения. Таков путь полного наблюдения за Луной. Что касается частных вопросов, то можно использовать для них каждое из наблюдений, как мы покажем ниже.

Об определении времени оборотов Луны¹²⁶

При наблюдении Луны нашли, что она не похожа на Солнце и не совершает одинаковых оборотов относительно одной из неподвижных звезд или одной неподвижной точки за равные промежутки времени. Так же найдено, что Луна обладает неравенством, ускорением, замедлением и средним [движением]; имеется неравенство и по ее широте в каждом градусе эклиптики. Первое упомянутое неравенство не может быть объяснено эксцентричным кругом, не имеющим собственного движения, так как в этом случае были бы определены положения максимального, минимального и среднего движения, это неравенство вызывается эксцентричным кругом, перемещающимся на равные дуги и переносящим [Луну] вперед и назад. Определили, что такое [изменение происходит] по причине эпицикла. В частности, было установлено, что наибольшее неравенство наблюдается в те сутки, когда Солнце диаметрально противоположно [Луне] и во время затмений, и неравенство меньше наибольшего неравенства в квадратуре Солнца. Это может быть только на эпицикле, а эпицикл должен быть на эксцентричном круге. Иногда эпицикл бывает ближе, и в этом случае его радиус [при движении] по эклиптике больше, а иногда [эпицикл] 54 дальше, что приводит к меньшему [радиусу его].

Из этого вытекает, что эпицикл [Луны] движется по эксцентричному деференту, к которому эпицикл относится как Солнце к его эксцентричному кругу, движение [Луны] по эпициклу не подобно движению эпицикла по деференту. Иначе промежутки времени ее возвращения были бы равны, как было сказано. [Движение Луны] также не быстрее [движения эпицикла], иначе ее возвращение по эпициклу, являющееся возвращением ее неравенства, казалось бы возвращением по долготе, то есть возвращением движения к среднему. Было найдено, что движение [по эпициклу] отстает, так что если [Луна] возвращается к этому неравенству и имеет такого рода неравенство, то возвращение произойдет при большей долготе.

Далее нашли, что отклонение Луны к северу или к югу от эклиптики не постоянно в одном и том же положении; если бы это было не так, то ее видимое возвращение было бы [одновременным] и по долготе, и по широте, то есть при ее возвращении в одной точке долготы она возвращается к той же широте, которую она имела в этой точке. Определили, что наклонный круг движется на запад в соответствии с ее движением, что эклиптика и наклонный круг не пересекаются постоянно в одной и той же точке, а [точка их пересечения] движется на запад в соответствии с движением наклонного [круга]. Если разделить величину разности между этими движениями за один оборот на сутки и часы, то получатся их доли. Из этого следует, что если бы пересечение имело место в неподвижной [точке], то затмения не могли бы происходить в любых местах и не было бы разности между широтами в любом месте, а отношение Луны к неподвижным звездам, которые приближаются и удаляются от нее по широте, оставалось бы одним и тем же.

Поскольку дело обстоит так, что среднее движение Луны можно найти не первым способом, упомянутым в главе о Солнце, а вторым: берется промежуток времени, содержащий полные лунные месяцы и несколько полных оборотов по долготе вместе с избыточной дугой, которая повторяется, по той причине, что она обязательно должна быть в каждом таком промежутке времени с такими оборотами по долготе, число которых такое же [как число дуг]. Если имеется избыток, то число возвращений неравенств будет таким же. Если бы не было возвращения неравенств, то обороты по долготе не были бы подобными. Астрономы старались, чтобы возвращения по широте за те же промежутки времени были подобны; это осуществляется, если концы этих [возвращений] имеют подобные состояния при затмениях Луны. Если положение с широтой отличается [от этого], то они проводят для нее специальное наблюдение. При полных лунных оборотах месяцы не должны быть полными, так как за один месяц Солнце [также] проходит некоторое расстояние и Луна не догонит Солнце. Поэтому в этом случае необходимо прибавить к возвращениям по долготе дугу до полного месяца, каждый раз прибавление всегда равно этой дуге.

Этим способом древние смогли определить промежутки времени между месяцами. Это проводится с помощью нахождения [времени] каждого возвращения к противостоянию или к соединению¹²⁷. Легче [использовать] противостояние, [чем соединение], из-за [свойств] затмения. Когда затмения повторяются, то месяцы становятся известными. Что касается того, что нужно сделать, чтобы возвращения неравенства были полными, то мы 55 покажем это вскоре.

Это можно сделать, когда затмения, ограниченные концами месяцев, происходят в одной и той же точке, северной или южной, что узнается при равенстве величины затмения и постоянстве расстояния от Земли, а также при подобии времени между началом и соединением. Если [Луна] возвращается ко всем своим неравенствам во всех случаях, то древние при наблюдении этих времен относительно неподвижных звезд нашли во всех случаях промежуток времени в шесть тысяч пятьсот восемьдесят пять и одна треть суток, за которые совершается двести сорок одно возвращение по долготе. Солнце [за этот промежуток] сверх оборотов проходит десять и две трети градуса. [За этот промежуток совершается] двести тридцать девять возвращений аномалий, двести сорок два возвращения по широте и двести двадцать три месяца. Они называют это время «периодическим временем», так как за это время обстоятельства повторяются еще раз. Стремясь [избавиться от] дробей суток, они увеличивают это в три раза; вместе с ним увеличивается и [число] возвращений; они называют полученное время «вычисленным извлеченным временем».

Когда Гиппарх рассмотрел свои наблюдения и наблюдения древних вавилонян и халдеев, которые жили в Халдее¹²⁸, он написал, что полученные ими результаты ошибочны и что промежуток времени, охватывающий это, составляет сто двадцать шесть тысяч семь суток и один прямой час. Он нашел, что это составляет приблизительно четыре тысячи двести шестьдесят семь месяцев,, четыре тысячи пятьсот семьдесят три возвращения аномалии и четыре тысячи шестьсот двенадцать оборотов по> долготе по эклиптике без семи с половиной градусов, которых недостает Солнцу. Это [вычисление] производилось по отношению к неподвижным звездам. Средний месяц равнялся у него двадцати девяти суткам тридцати одной минуте пятидесяти секундам восьми терциям и двадцати квартам¹²⁹. Он определил месяцы с помощью затмений. Если бы он вычислил их с помощью соединений и противостояний, то полученные им числа были бы меньше. Этот способ [состоит] в том, что находится общее число, которое делит число месяцев, т. е. четыре тысячи двести шестьдесят семь и число оборотов аномалий, то есть 4573; эти два числа делятся на [общий делитель] и получается двести пятьдесят один месяц и двести шестьдесят девять возвращений аномалий.

Что касается числа возвращений по широте, то он не нашел его при этих затмениях по указанному условию, так как стороны величин не одни и те же. Если он хочет найти возвращения по широте, он должен рассмотреть промежуток времени больше пяти тысяч четырехсот пятидесяти восьми месяцев и пяти тысяч девятисот двадцати трех оборотов по широте. Если принять результаты Гиппарха, разделить этот промежуток на 56 число месяцев, то ясно, что получится [число] суток в месяце. Если же разделить возвращения после их перевода в градусы на [число] всех суток, то получится продвижение за одни сутки как по долготе, так и по широте или по аномалии.

Градусы среднего [движения] по долготе могут быть вычислены более легким способом. Средний месяц является полным оборотом вместе с дугой прохождения Солнца за известное время среднего месяца. Полный оборот вместе с дугой Солнца известен, поэтому средний месяц Луны известен.

Птолемей пожелал рассмотреть то, что установил Гиппарх, и проверить его. Он изобрел способ более легкий, чем способ Гиппарха, добавил его к первоначальному, объяснил трудность применения этого способа, связанную с неравенством, имеющим место при движении Луны, так как если промежутки времени возвращений по долготе равны, то обороты не обязательно должны быть подобными из-за неравенства, имеющего место и для Солнца и для Луны. Что касается Солнца, то нужно обеспечить, чтобы дуги, которые оно проходит после оборотов, были равными, а это не всегда наблюдается из-за неравенств; бывает так, что промежутки времени между месяцами совпадают [друг с другом], а избытки Солнца и Луны не равны. Например, в случае Солнца, если промежуток времени — половина года, и в первом [промежутке! оно движется по дуге, начинающейся от [точки] среднего движения в Рыбах, то, как мы знаем, за половину года оно проходит половину эксцентричного круга и меньше половины эклиптики на 4;45 [градусов]. Если во втором [промежутке] оно движется после возвращения от [точки] среднего движения в Деве, то за половину года оно проходит половину эксцентричного круга и больше половины эклиптики на 4;45 [градусов]. Поэтому оно проходит равные [части] эксцентричного круга, но не равные [градусы] эклиптики. Однако нужно добиться того, чтобы при прохождении Солнца совсем не было бы неравенства или было бы одно и то же неравенство. Для этого нужно, чтобы имелись полные обороты Солнца на орбите Луны, а дробные их [части], представляющие собой две дуги, прибавлялись бы к первоначальным [оборотам] на половине, начинающейся от апогея и до перигея в первом промежутке времени и на половине от перигея до апогея — во втором, для того, чтобы не было неравенства или чтобы начало и конец обоих [промежутков] времени было бы в одной и той же точке неравенства, а это не бывает в последовательных [промежутках] времени, или чтобы начало обоих [промежутков] времени было бы на равных отрезках от концов двух разных расстояний. Например, Солнце начинает [движение] в на: чале затмения первого [промежутка] времени на некотором расстоянии от апогея и перигея в одной стороне, а в конце второго [промежутка] оно находится на таком же расстоянии [от них] с другой стороны. Или, например, Солнце начинает движение из точки на каком-то расстоянии от апогея, завершает обороты у апогея и к этому прибавляется дуга, чтобы быть на таком же расстоянии от апогея, как расстояние первой точки, где оно начало [движение]. То же самое наблюдается и в отношении перигея при условии, чтобы оно имело бы одно и то же неравенство и чтобы дуги, прибавляемые к полным оборотам по эклиптике, были бы равны.

То же самое должно быть и для Луны. Может случиться, что возвращения Луны в эклиптике за равные промежутки времени 57 равны, но [из этого] не следует, что она возвращается к той же аномалии, что и при начале [движения] , или к той же широте. Что касается аномалии, то аналогично тому, что мы сказали о Солнце, если Луна движется после оборотов, начиная от начала первого [промежутка] времени, [изменяя] свою скорость от быстрой к медленной, а во втором [промежутке] — от медленной к быстрой, то мы увидим, что за два равных [промежутка] времени она проходит равные дуги эклиптики по долготе, хотя за каждый из этих [промежутков] времени она не заканчивает оборота неравенства и не возвращается к первому неравенству. Это служит примером того, что она не имеет никакого избытка неравенства в одном из двух [промежутков] времени. Точно так же будет, если она в каждом из двух промежутков времени [начинает] двигаться из одного и того же положения относительно избытка или недостатка и вернется к тому же положению, но разность неравенства будет одна и та же и окажется, что она прошла равные дуги эклиптики, хотя и не вернулась к тому же неравенству. Этого нельзя избежать.

Если два начала движения на дугах находятся на равных расстояниях от апогея или перигея с обеих его сторон, то, как мы сказали о Солнце, окажется, что Луна начала [движение] из некоторой точки, закончила оборот в ней, затем оказалась в апогее или в перигее, затем закончила обороты у апогея или у перигея, а затем добавила дугу, равную той, которую она добавила в первой сфере. Поэтому мы видим, что она прошла равные дуги эклиптики, но не вернулась к своему неравенству.

Что касается широты, то о ней было сказано раньше. Необходимо выбрать для неравенства и для широты то, что обеспечивает эту разницу. Для неравенства необходимо, чтобы начала имели бы большое неравенство по величине в действительности или потенциально. Это более предпочтительно и правильно, хотя можно обойтись и без этого, и имеет место в действительности, если начало расстояний — с большим неравенством и если Луна начинает движение в одном промежутке времени с замедлением и сохраняет это движение так, чтобы она не окончила его ни с ускорением, ни с замедлением. В таком случае неравенство увеличивается особенно в конце первой четверти или трех четвертей круга, когда предел разности удваивается, при этом [Луна] не возвращается к двум упомянутым [началам] и нельзя видеть, чтобы за равные промежутки времени она прошла равные дуги по долготе или чтобы она закончила возвращение. Это имеет место потенциально, если в одном промежутке времени Луна начинает движение со среднего движения и приближается к быстрому, а в другом промежутке — начинает со среднего и приближается к медленному. Если при этом движении она будет в [конце] первой четверти или трех четвертей, то предел разности удвоится, а если же она будет в середине, то увеличивается в четыре раза. Потенциальное неравенство может быть больше этого, и ошибки не должно произойти. Поэтому Луна проходит равные дуги эклиптики, когда она еще не закончила возвращения неравенства.

Гиппарх исправлял неравенства Солнца, заставляя его начинать в одном промежутке времени с большим ускорением и не кончать с замедлением, а в другом — наоборот. Что же касается широты, то упомянутое выше служит для предосторожности при нахождении узла.

Ясно, что этот способ не легкий, хотя он 58 дает возможность наблюдать за искомым, если учитывать все, что сказано о нем.

Однако месяцы и обороты по долготе, найденные Птолемеем тем способом, он добавил к древним. Они совпадают с тем, что нашел Гиппарх; а [найденные им] неравенство и широта расходятся: он нашел более длинный промежуток времени для неравенства и более короткий для широты.

О частных и равномерных движениях Луны

Прежде чем начать исследования этого добавления, Птолемей построил таблицу движения Луны по долготе, неравенству и широте с помощью того, что он получил. Он установил движение Луны по долготе делением градусов одного оборота и дуги среднего прохождения Солнца за один месяц на [число суток] в месяце, что дает приблизительно 13; 10, 34, 58, 33, 30, 30 [градусов] для одних суток. Затем он разделил это на часы и их части, умножил число оборотов неравенства на 360, чтобы сделать их градусы, разделил полученное на [число] суток в том промежутке времени, который был у Гиппарха, и получил, что равномерное движение среднего неравенства за сутки [равно] 13; 3, 53, 56, 29, 38, 39 [градусам]. Однако, когда он проверил это своим методом, он нашел его меньше; он нашел, что в сутках 13; 3, 53, 56, 17, 51, 59 [градусов]. Затем он разделил это на часы. Точно так же он действовал для оборотов по широте и получил, согласно принципу Гиппарха, за одни сутки 13; 13, 45, 39, 40, 17, 19 [градусов], а согласно его исследованию, получилось больше, а именно 13; 13, 45, 39, 48, 56, 37, 45.

Мы покажем, что средняя элонгация¹³⁰ представляет собой движение на эксцентричном [круге]. Элонгация — это удаление Солнца от Луны и поэтому есть разность между их средними движениями, равная 12; 11, 25, 41, 20, 17, 59 [градусам] в сутки. Разделив это на часы и их части и умножив на [число] суток полных месяцев, а именно тридцать, а затем на [число] суток египетского года¹³¹, а именно триста шестьдесят [пять], и отбросив из всего этого полные обороты, Птолемей нашел то, что остается. Затем он умножает на восемнадцать для того, чтобы построить таблицу¹³², состоящую из трех соединенных таблиц, одна из которых для количеств лет, последовательно превышающих [друг друга] на восемнадцать лет; вторая — для каждого отдельного года до восемнадцати лет, за которыми часы, а третья — для месяцев, за которыми дни. Каждая таблица содержит один столбец для движений по долготе; другой — для движения по неравенству; третий — для движений по широте; четвертый — для движения по элонгации. Каждый столбец разделен по широте на шесть разрядов.

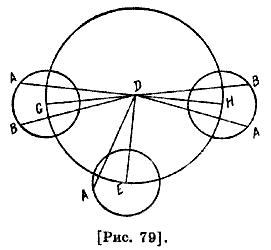
О том, что Луна имеет одно и то же неравенство как относительно эксцентрического круга, так и относительно эпицикла

Птолемей начал с объяснения способа, который он дал специально для определения движения по аномалии.

Сначала он сказал: хотя у Луны имеются второе и третье неравенства, отличные от тех, которые мы покажем и которые были упущены большинством наших предшественников, мы не будем говорить о них здесь, так как лунные затмения будут рассматриваться только в противостояниях, а второе и третье неравенства, оказывается, не имеют значительной величины в противостояниях. Второе неравенство является наибольшим в квадратурах, а третье — в двух гексагональных аспектах¹³³. Первое неравенство считается первым, так как оно может иметь место без других неравенств, тогда как последние имеют место только вместе с ним. Поэтому ему отдается предпочтение и речь вначале должна идти о нем¹³⁴.

Несмотря на то, что обстоятельства этого неравенства, то что происходит с ним и что следует из него, одни и те же 59 при эпициклической гипотезе и при эксцентрической гипотезе, предпочтительно основывать это неравенство при обоих гипотезах так, чтобы эксцентрический круг был бы деферентом эпицикла; это продолжение того, о чем мы говорили раньше. Что касается того, как из обеих гипотез по этому вопросу может вытекать одно и то же, в то время как движение по аномалии не подобно движению по долготе и не похоже на движение Солнца, где они подобны друг другу, и в то время, как отношение дуги, описанной по эпициклу ко [всему] кругу [эпицикла], меньше отношения дуги, описанной по эксцентрическому кругу ко [всему], то это доказывается тем, что мы утверждаем: деферент является концентричным, поскольку мы еще не рассматривали эксцентрического круга и не заменяем еще концентрический деферент эксцентричным, что необходимо приводит к первому неравенству. Что касается условия, которое нужно предположить для обеспечения постоянного наличия этого неравенства, когда Луна находится на эпицикле, находящемся на деференте, или на эксцентричном круге, а не на эпицикле, оно таково: движение эпицикла по деференту описало бы дугу, большую, чем дуга Луны, по эпициклу, и чтобы дуга эксцентрического круга, которую описывает Луна, когда она находится на нем, была бы подобна дуге эпицикла, но чтобы эксцентрический круг двигался по направлению, противоположному движению Луны, и описывал дугу подобной избытку дуги референта над дугой эпицикла и чтобы движение Луны происходило в сторону востока, было бы противоположно движению Вселенной. Рассуждение будет одним и тем же при обеих гипотезах, были ли отношения равны или подобны между собой. Допустим сначала, что они равны, и пусть ABC — концентрический [с эклиптикой] круг с центром D, имеющий полудиаметр AD и эпицикл EG вокруг центра С [рис. 70]. Пусть при движении [эпицикла] из А до С светило проходит из Ε до G; проведем CG и DСЕ. Тогда дуга АС будет больше дуги этого круга, подобной EG.

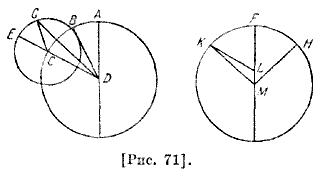
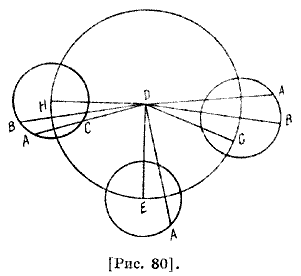
Пусть дуга ВС относится к кругу ABC как EG к своему кругу; проводим DB. Ясно, что угол ADB есть угол разности между средним движением и движением аномалии, а это есть предполагаемая нами величина движения эксцентра, когда Луна находится на нем, за равное время и по этой же гипотезе.

Возьмем DH, равную CG, и проведем HG; поскольку дуга ВС подобна дуге EG, то ясно, что угол BDC равен соответствующему ему углу GCE. Отсюда очевидно, что CGDH — параллелограмм. Если из точки Η на расстоянии HG опишем дугу FG, то она будет иметь требуемое отношение к эксцентру. Пусть линия HBF пересекает эту дугу в точке F, тогда внешний угол FHG эксцентра равен внутреннему соответствующему углу HDC, то есть внешнему углу GCE, поэтому дуга GF будет подобной EG. Следовательно, если светило опишет дугу FG, а линия FD — дугу АВ или же дугу EG, а его центр — дугу АС, то оно будет видно по одной и той же прямой и опишет одну и ту же дугу и, наоборот, оно не будет видно по другой прямой.

Он сказал: теперь докажем это, если указанные отношения 60 будут подобными по наблюдению.

Пусть HFK — эксцентрический круг с центром L, Μ — центр эклиптики, FК — дуга, описанная движением круга [эксцентра] так, чтобы они из эклиптики отсекли [дуги] в указанном отношении. Тогда угол HMF соответствует этим градусам эклиптики; соединим точки F, L и Μ на диаметре, проведем LK, МН и МК [рис. 71].

Пусть ABC — концентрический круг, имеющий центр D; и пусть центр его эпицикла прошел по нему дугу АС, а светило — по эпициклу дугу EG, подобную FK; возьмем АВ, подобную HF; проведем полудиаметр AD и [линии] BD, DG, CG и DCE. Поскольку DC к CG из треугольника DCG относится как LK к LM из треугольника KLM и углы L и С равны, так как они дополняются до двух прямых после прибавления двух равных углов GCE и FLK, то эти два треугольника подобны. Поэтому угол Μ равен углу G. Но ВС подобна FK, то есть EG; следовательно, углы BDC и GCE равны и BD, GC параллельны между собой; угол BDG равен углу DGC, то есть LMK. Однако было доказано, что угол ADB как разность [этих движений] равен углу HMF, таким образом, весь угол Μ равен ADG. Это то, что мы хотели доказать.

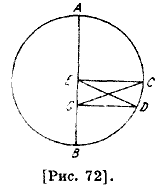
Об определении первого и простого неравенства Луны

После выяснения этого обстоятельства Птолемей перешел к выбору эпицикла для этого неравенства. Он считает, что Луна не имеет широты и как бы находится на плоскости эклиптики. Это облегчает выяснение того, что он рассматривает и позволяет обходить затруднения, связанные с вычислением широты, которая, как мы покажем позже, не вызовет существенного расхождения, если ее отбросить.

Однако сначала нужно представить себе, что на сфере несущей Луны имеются круг в плоскости эклиптики, концентричный с ней, и другой круг, наклоненный к ней на величину широты, центр которого совпадает с ее центром, и [круг, центр которого] равномерно движется [по этому кругу] вокруг центра эклиптики на величину избытка движения по широте над движением по долготе, так что его апогей перемещается, а в его плоскости находится эпицикл, движущийся по нему в сторону востока. Луна же движется в сторону Запада. Хотя это так, деферент считается находящимся на плоскости эклиптики.

Что касается выяснения величины неравенства, то прежде всего мы приведем предпосылки, полезные для этого предложения и для определения значений уравнения.

Мы утверждаем: если средняя дуга меньше полукруга, когда оба уравнения прибавляются или оба вычитаются, то уравнение между истинной и средней дугами за время прохождения средней дуги есть разность между двумя исходными уравнениями, которые определяются градусами [точек], ограничивающими этот промежуток времени¹³⁵. Докажем это сначала для случая эксцентрической гипотезы. Пусть круг ABCD — эксцентрический круг с центром Ε [рис. 72] и AЕВ — его диаметр, проходящий через оба центра, G — центр 61 эклиптики; пусть светило находится в D, тогда его уравнением, соответствующим градусу D, будет угол EDG. Если оно переходит в С, то его среднее движение за это время опишет дугу CD, а его уравнением, соответствующим градусу С, будет [угол] ECG; соединим D и С. Предположим, что оба эти уравнения различны. Пусть EDG больше ECG.

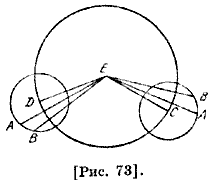
Мы утверждаем : очевидно, что углы ECD и EDC обязательно равны. Если мы отнимем из угла С угол GCE и прибавим к углу D угол EDC, то получатся углы GCD и GDC, являющиеся углами треугольника CGD. Поскольку угол EDG больше угла GCE, то прибавляемое больше отнимаемого. Поэтому углы GCD и GDC [вместе] больше углов ECD и EDC. Следовательно, угол CED треугольника EDC, соответствующий среднему [движению], больше угла CGD, соответствующего истинному [движению]. Поэтому избыток угла EDG над углом ECG будет уравнением между двумя дугами: видимой, то есть углом G, и средней, то есть углом Е. Это и есть разность уравнений, соответствующих двум градусам. Следовательно, если угол уравнения С будет больше угла [уравнения] D, то угол G будет больше угла Ε и разность уравнений будет по величине той же самой.

Докажем это для случая эпициклической гипотезы. Пусть CGD — концентрический круг с центром Ε; С и D — точки центров эпицикла, причем он перемещается из С в сторону D [рис. 73].

Когда центр эпицикла находится в С, то светило находится в А и уравнение, соответствующее градусу С, — угол СЕА; когда же эпицикл переходит в D, то светило переходит в В, уравнение, соответствующее градусу D, — угол DEB видимого круга эпицикла. Истинной дугой является дуга, противолежащая углу АЕВ, где А — точка эпицикла, находящаяся в С, а. В — точка эпицикла, находящаяся в D. Средней дугой является дуга, противолежащая углу CED; угол CED превосходит упомянутый угол АЕВ на угол BED, из которого вычтем угол АЕС. Разность между ними есть разность между углами двух дуг. Но угол BED больше угла DEA на угол АЕВ. Это и есть избыток уравнения градуса.

Точно так же, если мы предположим, что светило вначале находилось в В, затем перешло в перигей, потом — в апогей, затем — в А. Тогда видимый угол будет ΒΕΑ, где В — [точка] эпицикла, когда он находится в С; А — [точка] эпицикла, когда он находится в D. Этот угол превосходит средний, то есть угол DEC, на угол ВЕС, а средний 62 превышает этот на угол AED. Разность между этими избытками есть угол АЕВ, который и есть уравнение. Он же сам не что иное, как разность между двумя уравнениями градусов.

Если одно уравнение является прибавляемым, а другое — вычитаемым, то разность между двумя дугами, то есть уравнение между этими дугами, есть сумма этих двух уравнений. Докажем это сначала по эксцентрической гипотезе на том же круге, что был выше.

Пусть С — точка между перигеем и апогеем, a D — между апогеем и перигеем [рис. 74]. Указанная дуга есть дуга CAD; угол С — прибавляемое уравнение, а угол D — вычитаемое уравнение. Но угол видимости и истинная дуга есть сумма внутренних углов СЕА и AED, а средний угол есть сумма внешних углов СЕА и AED. Они превосходят сумму С и D, а их сумма есть разность уравнений.

Докажем это также для случая эпициклической гипотезы. Пусть уравнение АЕС — вычитаемое [рис. 75], а BED — уравнение прибавляемое. Тогда угол CED образует истинную дугу, а угол АЕВ — среднюю дугу, которая меньше видимой на сумму двух уравнений. Точно так же будет, если рассмотрим обе гипотезы совместно. Пусть угол С — вычитаемый, а угол D — прибавляемый [рис. 76]. Расположим линии углов в противоположных направлениях, что легко можно сделать.

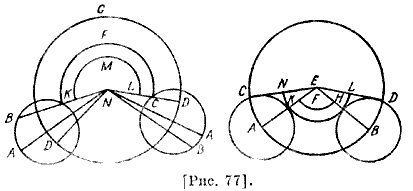
Мы утверждаем: из всего, что мы привели, вытекает, что если некоторая дуга образует прибавляемое уравнение, то дуга, дополняющая ее до круга, образует точно такое же, но вычитаемое уравнение. Если же эти уравнения одного и того же рода, то мы сделаем рисунок случая эксцентрической гипотезы.

Мы утверждаем: если светило про ходит CABD и возвращается к D, то видимая линия образует угол CGA, два прямых и угол BGD, а средняя дуга образует угол DEA, два прямых [угла] и угол BED, то есть угол CGA с прибавлением угла С, два прямых [угла] и угол BGD с вычитанием угла D. Таким образом, из предыдущего [угла] вычитается угол С и к нему прибавляется угол G. Вычтем угол С из D, получим, что вычитаемый [угол] есть избыток D над С. На такой же [угол] средняя дуга превышает дугу DC.

Что касается случая эпициклической гипотезы, когда оба уравнения однородные, то если эпицикл движется от D до С в сторону G, а светило — от А до В [рис. 77], то видимый угол и угол HFK известны и средний угол и угол LMN известны; поэтому средний 63 превосходит на угол СЕВ и меньше на угол AED; разность между ними угол ΒΕΑ. Из рисунка, где оба уравнения были неоднородными, известно, что их сумма также есть уравнение, но прибавляемое. Что касается случая эпициклической гипотезы, когда уравнения противоположные, то, что имеется в углах DEC после определения LMN, меньше того, что имеется в углах АЕВ после определения HFK, на два угла — DEB и АЕС, вместе взятых.

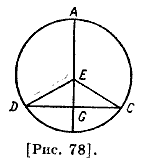
Точно так же и в случае эксцентрической гипотезы: два угла G со стороны А меньше двух углов Ε со стороны А на два угла — С и D вместе [рис. 78].

После установления этих вещей выясним положение двух уравнений в каждом из трех древних и современных затмений. Пусть эксцентрический круг EGH описан около D и пусть центр эпицикла в Ε [рис. 79]; когда центр в Е, то светило на 24;30 градусах Девы; затем оно заканчивает обороты, и центр проходит через Η до G. Светило движется из А в перигей, затем в В, что на 53;45 градусах Девы. Тогда уравнение прибавляется, и ADB будет известен.

Далее центр перемещается из G в Е, в Н, тогда светило перемещается из В в А пока не дойдет до С, что на 3;15 градусах Рыб. Центр перемещается на избыток углов GDH над двумя прямыми. Истинный перемещается на избыток углов BDC над двумя прямыми. Избыток среднего есть угол CDH. Если вычесть угол HDB, от GDB остается избыток среднего, то есть вычитаемое уравнение — угол ΒDΗ. 64

Так как дуга АСВ имеет прибавляемое уравнение, которое достигает рассматриваемой разности CKD между средним и истинным, то ее остаток, то есть дуга АВ, будет иметь вычитаемое уравнение такой величины из-за того, что мы показали. Вычитаемое уравнение дуги ВАС на 5;37 [градусов] меньше уравнения дуги ВА, то есть прибавляемого уравнения дуги АСВ, что [равняется] 3;24 [градусам]. Поэтому дуга АС должна иметь прибавляемое уравнение на величину избытка прибавляемого уравнения над вычитаемым уравнением, то есть на BEG, так как если светило находится в А, а. центр эпицикла в любой желаемой точке, например в G, как он есть на самом деле, то здесь нет разности; истинное пройдет остальные углы из ADC, когда [центр] эпицикла в G, а средний пройдет остальные углы из ADH. Превышение истинного будет на угол ADC. Это избыток уравнения АСВ над уравнением ВАС. На этот [угол] истинное превышает среднее.

Теперь покажем соответствующие обстоятельства в случае других трех затмений. Пусть Ε — место эпицикла при первом затмении [рис. 80], и Луна находится в А на 43;15 градусах Скорпиона. Пусть центр перемещается в G не через Н; когда центр достигнет G, светило будет в B на 25;10 градусах Овна; тогда среднее образует оставшийся угол EDG, а истинное — оставшийся угол ADB, который меньше среднего на сумму углов GDB и ADE. Далее центр перемещается из G в H, тогда светило будет в С на 24;05 градусах Девы.

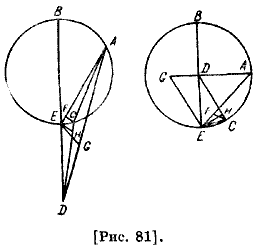
Тогда получится, что [среднее] перемещается на весь угол GDH, истинное — на сумму двух углов — ΒΌΑ и ADH, что превышает средний на угол BDG и меньше на угол CDH, являющийся частью угла ΒΌΗ, то есть BOG. Поэтому разность между ними, то есть угол BDC, и есть прибавляемое уравнение. Первое уравнение состояло из суммы двух углов — ADE и GOB, то есть ADG и GDB. Поэтому разность между этим и первым [уравнением] есть угол CD А, что тоже является прибавляемым уравнением, так как если мы представим себе, что оба центра и светило движутся и светило находится в А, когда центр находится, например, в точке F, то F должна быть там, где отношение угла дуги ADG у центра D к углу дуги ADB, пройденной [центром] эпицикла и светилом за один и тот же промежуток времени, будет таким же, как отношение двух движений у центра за один оборот или как [отношение] любых двух дуг, которые они проходят за один и тот же промежуток времени.

Допустим, [центр] пройдет дуги не больше полукруга и пусть F будет там, где G; тогда ценр пройдет угол HDG, а видимый угол CDA превышает средний на два угла — CDH и GDА. Если он пройдет дуги больше полукруга и дойдет, например, до Е, то среднее будет суммой двух углов — HDG и GDE, а видимое превышает их на столько же, на сколько он превышал там. Из этого вытекает, что если часть любой дуги прибавляемого уравнения превышает это уравнение на некоторую величину, то остальная часть превышает остаток уравнения. Было также доказано, что если часть любой дуги прибавляемого уравнения меньше этого уравнения на некоторую величину, то 65 остальная часть превышает [остаток] уравнения на величину избытка прибавляемого уравнения над вычитаемым.

Теперь мы утверждаем: апогей может находиться только на дуге АВ. Если дуга ВСА с прибавляемым уравнением, то дуга АВ — с вычитаемым уравнением, причем на столько же, на сколько то превышает. Это легко установить из сказанного выше.

Теперь вернемся к книге. Мы говорим, что Птолемей использовал три древних и три современных затмения и вычислил на их основе геометрическим путем неравенства движения Луны. Что касается древних, то Солнце в середине промежутка первого из них по истинному времени в Александрии согласно началу эпохи было на 24;30 градусах Рыб. Это можно установить по историческим записям, по которым известны год, месяц, день и час, когда в Вавилоне произошло это затмение. [Разность] долгот между Вавилоном и Александрией известна, поэтому известен час этого затмения в Александрии. Он получил среднее [движение] Солнца относительно Александрии, поскольку там [проводилось] его измерение, и затем исправил его.

Что касается второго затмения в середине второго затмения, то, согласно тем же измерениям, Солнце было на тридцати с половиной и четвертью градусах Рыб; поэтому Солнце и Луна после отбрасывания полных оборотов прошли триста сорок девять градусов пятнадцать минут, а время между этими затмениями, согласно историческим записям, — триста пятьдесят четыре суток и два с половиной абсолютных часа, или, если учесть поправки неравенств суток, два часа тридцать четыре минуты.

В середине третьего затмения Солнце было приблизительно на трех с четвертью градусах Девы; поэтому разница [от второго до третьего] — сто шестьдесят девять градусов тридцать минут, а прошло 176 суток и двадцать с половиной абсолютных часов, или с поправкой двадцать и одна пятая часа.

Поэтому, по мнению Гиппарха, в первое время Луна пройдет [за вычетом полных кругов] триста шесть градусов и двадцать пять минут по аномалии, а по долготе — триста сорок пять градусов и пятьдесят одну минуту.

Если уже известны величина дуги исправленного прибавления и величина средней дуги, то разность между установленными по наблюдениям дугами будет уравнением, которое дают величины дуг; она равна разности между уравнениями двух дуг или сумме этих уравнений, как мы доказали выше в случаях обеих гипотез. Если сравнить положение, установленное по наблюдению, со средним за этот промежуток времени, то получится дуга уравнения по эклиптике 3;24 прибавляемых [градусов] , а за второй промежуток времени избыток по аномалии будет 150; 26 [градусов], а по долготе 170;07 [градусов] , а уравнение — 37 вычитаемых минут.

Птолемей привел рисунок, в котором показал всю дугу, отсеченную линией, выходящей из центра эклиптики до точки Луны на эпицикле или до точки Луны на эксцентре, самой отдаленной от точек трех затмений. На дуге, проходящей через три точки [затмений], он отсекает дугу и доказывает, что по эпициклической гипотезе центр эпицикла не может находиться на хорде этой отсеченной дуги. Это привело его к вычислению отношения [между] диаметрами концентрического [круга] и эпицикла. После того, как он на этом же рисунке определил линию, выходящую 66 из глаза до Луны, которая полностью пересекает эпицикл, и ее часть является хордой эпицикла.

Пусть имеется концентрический круг и на нем в одном из двух рисунков находится эпицикл, а во втором — эксцентрический круг. Пусть А — место Луны в середине первого затмения и она движется из А в сторону С, заканчивает обороты и [доходит] до В; затем движется из В, заканчивает обороты и достигает точки С третьего затмения. АСВ и ВАС известны по методу Гиппарха, в котором небольшое изменение, вызванное перемещением этих [дуг], не оказывает влияния на само время. Если дуга АСВ будет с прибавляемым уравнением на 3;24 градуса и АВ, [дополняющая] до полного оборота, будет с вычитаемым уравнением на ту же величину, а дуга ВАС будет с вычитаемым уравнением на 37 минут, то дуга АС будет с прибавляемым уравнением на величину, незначительно отличающуюся от величины вычитаемого уравнения дуги ВА; то есть от 3;24 [градусов], а именно на 37 минут, и поэтому равна трем градусам двадцати четырем минутам без тридцати семи минут. Зная величину этого из рисунка, представляющего указанное соотношение, можно с помощью вычисления найти, что прибавляемое уравнение АС есть два градуса и сорок семь минут. Если прибавить к этому тридцать семь минут, то получится 3;24 [градуса].

Далее ясно, что перигей не находится на дуге ВАС, так как она меньше по расстоянию, это произойдет при другом расстоянии.

Пусть центр эклиптики, то есть D, будет внешним по эпициклической и внутренним по эксцентрической гипотезе. Соединим его с тремя точками, как на этих двух рисунках [рис. 81], линиями DB, DA и DC.

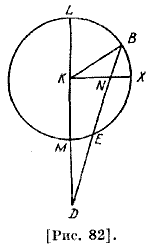
В [рисунке] эксцентрической гипотезы продолжим BD до Е, а в [рисунке] гипотезы эпицикла Ε обозначает точку пересечения круга с линией BD; из Ε опустим перпендикуляр ЕН к CD и EG — к AD, а из С — перпендикуляр CF к АЕ. То, что стягивает ВА из эклиптики по эпициклической [гипотезе], известно, поэтому угол BDA известен. Также по эксцентрической гипотезе [ВА] стягивает из эклиптики то, что между местами двух затмений, которое известно; поэтому угол BDA известен. Угол D прямой, поэтому соотношение углов [и сторон] треугольника GDE известно, известны также его стороны. Угол ΒΕΑ известен из дуги АВ, поэтому остальной угол AED известен. Угол G прямой, поэтому углы и стороны треугольника AEG известны. Так как дуга ВАС известна, то угол BDC, стягиваемый дугой уравнения по эпициклической гипотезе, известен. Соответствующий ему [угол] по эксцентрической гипотезе со стороны двух восстановленных расстояний известен. Оставшийся угол EDH известен. Также Η — прямой, поэтому углы и стороны треугольника DEH 67 известны. Если отнять два известных по дуге угла ΒΕΑ и АЕС, то оставшийся угол СЕН известен. Но угол СНЕ прямой, поэтому углы и стороны прямоугольника EHD известны по обеим гипотезам.

Мы легко найдем также соотношение углов и сторон двух треугольников — FCE и ACF. Отношение линии АС ко всем известным линиям будут известны. Но ее отношение к диаметру известно, поэтому отношение линии СЕ к диаметру также будет известно и дуга СЕ будет известна. Тогда вся дуга ВАС будет известна и хорда BE будет известна и будет иметь известные отношения ко всем линиям. Линия BE будет равняться 117 частям 37 минутам и 32 секундам диаметра. Поэтому она меньше диаметра, ВАСЕ меньше полукруга, и центр эпицикла не находится на ВАСЕ.

Пусть центр эпицикла — точка К [рис. 82] ; продолжим DMK до L, L — апогей, Μ — L — апогей, Μ — перигей. Если прибавить к [произведению] DL на DM [произведение] известной КМ на себя, что можно найти, то получится [произведение] KD на себя. Таким образом, KD известна и DL будет также известна. По вычислению получается, что КМ относится к KD как 5;13 к 60.

Опустим из К перпендикуляр KN к BE и [продолжим] его до X. Он разделит пополам дугу BE и хорду BE. Найдя величину KD и ND и доказав, что угол N прямой, можно быстро определить углы треугольника KND. Также, найдя NK и KB и доказав, что угол N прямой, ты определишь углы треугольника KBN. Тогда ты определишь два угла при К, то есть весь угол DKB и оставшийся угол BKL. Поэтому ты определишь дугу BL, а затем дугу MB, дополняющую ее до полукруга. По вычислению получается, что дуга BL, то есть расстояние Луны до перигея в середине второго затмения, [равна] 12;24 [градусам], а угол KDВ — 59 минутам; это величина дуги LB, которая стягивает из эклиптики. Поэтому получается, что середина [второго затмения] была на 14; 44 [градусах] Девы, а исправленное, как мы сказали, было на 13;45 [градусах] Девы.

Рассматривая три современных затмения, он показал, что положение Солнца в первом из них на 13;15 [градусах] Тельца, а Луна, противоположная ему, в Овне, в третьем — на 14;30 [градусах] Рыб, а Луна, противоположная ему, — в Деве. Между первым и вторым затмениями прошел один египетский год, сто шестьдесят шесть суток и двадцать три с половиной с одной восьмой частью прямых абсолютных часов, или двадцать три с половиной с одной четвертью часов, а дуга, отсеченная серединами [этих затмений], составляла 16;55 [градусов].

Между вторым и третьим [затмениями] прошел один египетский год, сто тридцать семь суток и пять с половиной прямых 68 абсолютных часов, а отсеченная дуга составляла 137;55 [градусов]. Во втором затмении имеется вычитаемое уравнение на 7;42 [градусов], так как среднее [движение] Луны за этот промежуток времени равно 169;37 [градусам] после отбрасывания [полных] оборотов, что превышает исправленное на эту величину. Однако избыток дуги по аномалии после [полных] оборотов равен 110;21 Градусам] ; эта величина стягивает величину уравнения из эклиптики. Третье затмение имеет прибавляемое уравнение на 1;21 [градус], так как среднее [движение Луны] равно 137:32 [градусам] после отбрасывания [полных] оборотов, а это превышает исправленное, которое прибавляет ту же величину, так как дуга, оставшаяся после [полных] оборотов при движении по аномалии, за этот промежуток времени составляет 81; 36 [градусов]. Эта величина стягивает [упомянутую] величину уравнения.

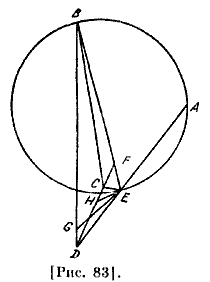
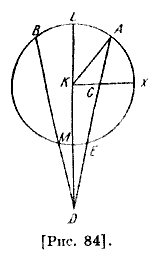
Если мы сделаем для этих трех затмений такой же рисунок, как для первых трех, то выяснится, что дуга АВСЕ больше полукруга и что центр эпицикла находится на ней; легко определяются соотношения линий и углов [рис. 83]. [Сначала] находятся величины дуг СЕ, ВС и BE, из чего выясняется, что апогей находится на дуге ВА, так как дуга А В меньше на 7; 42 [градусов] и [равна] 110;21 [градусам]. Дуга ВС превышает уравнение на 1; 21 [градус] и она [равна] 81;36 [градусам]. Поэтому дуга СЕА должна превышать на оставшиеся градусы, то есть на 7; 21 [градусов]. Таким образом, каждая из двух дуг — ВС и СЕА имеет прибавляемую дугу и поэтому апогей не находится на них, а остается на АВ. По вычислению линия АЕ получилась 88; 40; 17.

Если это уже выяснилось, то также, на таком же рисунке, приведенном для трех первых затмений, тем же способом определить величину линии КМ относительно KD; по вычислению это оказалось 5;14 к 60.

На таком же рисунке [рис. 84] и тем же способом может быть определена величина дуги AL; по вычислению она оказалась 5;43 [градусов]. Оставшаяся дуга LB, то есть расстояние Луны во втором затмении, будет составлять 64;38 [градуса], если дуга АВ содержит 110; 21 [градусов]. Угол LDB, который вычитается из среднего движения, равен 3;20 [градусам]. Поэтому среднее [положение] Луны будет находиться при этом на двадцати девяти градусах и тридцати минутах Овна¹³⁶.

Об исправлении равномерных движений Луны по долготе и аномалии

Если это уже выяснено, то [теперь переходим] к исправлению среднего движения Луны и ее аномалии. Это легко сделать, если найти промежуток времени между древними и современными затмениями, например, между вторым затмением из древних и вторым затмением из современных. Этот промежуток времени равен восьмистам 69 пятидесяти четырем египетским годам, семидесяти трем суткам и двадцати трем с одной третью [часам]. За этот промежуток к [полным] оборотам по долготе прибавляется 224;46 [градуса], а по аномалии — 52;31 [градуса]. Это сходится с тем, что следует из предыдущих принципов относительно долготы, но расходится с ним относительно аномалии, которая больше на семнадцать минут. Если разделить это на [число] дней упомянутого промежутка времени, то получится доля одного дня, которую следует вычесть от [среднего дневного движения]; это одиннадцать кварт, сорок шесть квинт и тридцать девять секст. Исправленное дневное [движение аномалии] будет 13; 3, 53, 56, 17, 51, 59.

Об эпохе равномерных движений Луны по долготе и аномалии

Далее он получил эпоху [среднего движения по Эре] Набонассара¹³⁷ с помощью определения времени между ней и вторым из древних затмений таким же образом, как он сделал в случае Солнца.

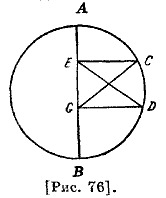
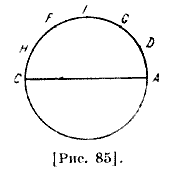
Об исправлении движений Луны по широте и об их эпохе

Птолемей, переходя к выяснению обстоятельства широты, сказал: в этом мы последовали Гиппарху, у нас получилась ошибка относительно широты Луны; по мнению Гиппарха, Луна укладывается в своей орбите приблизительно шестьсот пятьдесят раз, а в круге [земной] тени, примыкающем к среднему расстоянию в двух соединениях, — два с половиной раза. Предположив это и найдя величину широты, мы смогли судить о величинах частных затмений и определить границы, после чего наступит затмение Луны. Из этого мы установили средние движения по широте через определение величины затемненной части в середине времени [затмения] и определение ее широты в середине времени этого затмения у определенного узла¹³⁸. Затем мы находим движение по широте, для чего возьмем промежуток времени между затмениями с одинаковыми величинами затмений и с известными широтами, так как известны продолжительность затмения и долгота. С помощью упомянутого метода по наблюдаемому среднему движению мы находим избыточное уравнение исправленного движения. С помощью среднего [движения] мы находим эпохи [движения] по широте и избыточную дугу после [полных] оборотов. Он сказал: в настоящее время мы пользуемся более современными методами, избавляющими от применения тех принципов. Когда нам удалось уточнить среднее [движение] по широте, действуя обратно, мы заново исправили движение по широте, а затем исправили те самые принципы, установили их негодность.

Что касается того метода, которому мы следовали, то [его суть такова] : берем промежуток времени между затмениями, равными по величине тьмы, по времени [прохождения] середины затмения и по стороне. Если удается, то мы берем эти затмения у одного и того же узла, то так и сделаем, а если не удается, то допустим, что они у двух узлов. Мы знаем, что когда затмение обладает указанным свойством, то Луна точно возвращается к своей широте, так как два затмения могут быть подобными только при одинаковой величине захода. Если же при одном затмении Луна находится во Вселенной ближе к Земле, то круг тени при этом будет шире, а при другом затмении — наоборот. Когда она находится 70 ближе, она затемняется на какой-то промежуток времени и имеет некоторую широту, то есть расстояние до эклиптики, а во втором случае она [начинает] затемняться только тогда, когда ее широта меньше той широты. Однако если [все-таки] это случится, то не будут равны ни время середины затмения, ни [промежутки] времени между началом и появлением. Если же эти времена равны при подобии величины затемнения, то определяется, что оба затмения произошли примерно в одном и том же отрезке¹³⁹.

Он сказал: при одном из рассматриваемых нами наблюдений имелись два подобных затемнения у одного и того же узла и в одной и той же стороне [эклиптики] ; узел был нисходящий¹⁴⁰, сторона южная, а величина — шестая часть диаметра, то есть в два пальца¹⁴¹. Первое из этих затмений наблюдалось в Вавилоне, а второе — в Александрии. Между ними шестьсот пятнадцать египетских лет, сто тридцать трое суток, двадцать один с половиной с одной третью равноденственного часа. Что касается расстояния, то оно было близко к [полученному] в середине.

Из даты и эпохи было найдено, что при первом из них расстояние Луны от апогея эпицикла было 100;19 [градусов], а при втором — ее расстоянии от апогея с другой стороны было 251;53 [градус]. Ее исправленное место при первом] было меньше среднего на пять градусов, а при втором — больше на четыре градуса пятьдесят три минуты. Она [по исправленному движению] вернулась к своей широте, а по среднему отставала от полного оборота на сумму двух поправок, то есть на девять градусов и пятьдесят три минуты. По принципам Гиппарха, оба уравнения, [вместе взятые], за этот промежуток времени должны быть больше этой величины на девять минут, так что их сумма равнялась приблизительно десяти градусам и двум минутам. Поэтому движение по широте, по его принципам, меньше того, что нашел Птолемей. Птолемей раз делил эти девять минут на промежуток времени и прибавил долю одних суток к суточному среднему движению по широте, записанному Гиппархом. Величина этого прибавления 0; 0, 0, 0, 8, 39, 18. Птолемей привел еще два затмения¹⁴², совпадающих по всем показателям, кроме узла: первое — это одно из трех вавилонских затмений, которое произошло у восходящего узла, а другое — у нисходящего узла; оба они южные, то есть Луна затмилась с южной стороны на величину четверти диаметра, то есть на три пальца. Для определения этого он нарисовал рисунок [рис. 85]. Он построил наклонный круг ABC с диаметром АС, где А — восходящий узел, С — нисходящий узел, а В — северный конец.

При первом затмении Луна находилась в D, так как, когда затмение со стороны юга, центр Луны оказывается к северу от эклиптики. При втором [затмении] она находилась в Е. AD и СЕ должны быть равны между собой.

Если мы еще этого не знаем, то можно вычислить дату по эпохе и найти среднее движение Луны по долготе и аномалии; из ее движения по аномалии следует, что расстояние Луны до апогея эпицикла при первом [затмении] составит 12;24 [градусов]. Затем, определив величину ее поправки, можно найти, что ее исправленная величина будет меньше среднего на пятьдесят девять минут. Это и есть ее поправка.

Расстояние Луны от апогея [эпицикла] будет равно 2;45 [градуса], а вычитаемая поправка — тринадцать минут. Пусть середина Луны при первом [затмении] будет в G, так что DG является вычитаемой 71 поправкой, а при втором — в H, так что ЕН является вычитаемой поправкой; их величины известны. Так как промежуток времени между затмениями известен, — он [равен] двумстам восемнадцати египетским годам, тремстам девяти суткам и двадцати трем и одной двенадцатой равноденственного часа, — то избыточная дуга над [полными] оборотами при среднем периодическом движении Луны по долготе известна. По вычислению она составляет сто шестьдесят градусов и четыре минуты. К ней прибавляется поправка первого затмения и из нее вычитается поправка второго затмения. Полученная дуга DE будет в середине полукруга, тогда остальная часть разделится на две половины. Если расстояние до двух узлов одно и то же, то одна половина оставшейся дуги есть AD, а вторая — дуга СЕ. Но вычислению [каждая из них] равна 9;35 [градусам].

Определяются [также] дуги AD и СН среднего движения в обоих [затмениях], находятся их расстояния до северного конца и до средней точки. Из этого он определяет эпоху Луны по ее широте для даты Набонассара.

Далее Птолемей приводит таблицу для первой поправки143, в которой [сначала] приведены градусы по аномалии через каждые шесть градусов и через три градуса; это сделано в двух столбцах, как в случае Солнца. В третьем столбце он дает прибавляемые и вычитаемые поправки, где показано, сколько градусов поправки соответствует [для градусов аномалии, взятых] через каждые шесть [или три] градуса, а вопрос о том, когда следует ее прибавить или вычитать, — ясный¹⁴⁴.

О том, что принятая Гиппархом разница величины [лунного] неравенства получается не из-за принципов, по которым он действовал, а вследствие вычисления

Далее Птолемей перешел к выяснению причины допущенной Гиппархом ошибки в величине движения по аномалии и в величине отношения полудиаметра эпицикла к полудиаметру деферента. По гипотезе эксцентра оно должно быть равным отношению шести и одной четверти к шестидесяти, а по гипотезе эпицикла — отношению четырех градусов и сорока шести минут к шестидесяти. Поэтому для них величина максимальной поправки будет разной, так как в первом случае она достигает 5; 49 [градусов], а во втором — 4;34.

По исследованию Птолемея установлено, что в обоих случаях это отношение равно отношению 5;15 к 60 и что максимальная разность составляет пять градусов. Он упомянул, что это произошло у [Гиппарха] не по причине ошибочных принципов, а по причине ошибочного вычисления. Затем показал, как это [случилось], и сказал: здесь подействовало не одно, а разные обстоятельства: допущена ошибка или в наблюдении, или в вычислениях промежутков времени эпохи и даты. Он сказал: Гиппарх рассматривал три затмения, наблюдаемых в Вавилоне, и одинаково поступил с ними; для первого он нашел дату, промежуток времени между ним и началом эпохи и время, на которое отличаются времена Вавилонии и Александрии, и определил, в каком часу середина [затмения] наступила в Александрии. Исходя из этого он определил среднее и исправленное положения Луны. Таким же образом он поступил со вторым затмением и [нашел] промежуток времени между ними. Так же он поступил и с третьим.72

Птолемей обнаружил, что у Гиппарха допущена ошибка в [вычислении количества] часов промежутка времени между первым и вторым затмениями, так как при проверке оно оказалось превышающим полные дни [и часы] на три пятых часа, тогда как Гиппарх считал, что оно превышает на половину и одну четверть часа. При проверке оказалось, что избыточная дуга при движении составляет 173;28 [градуса], а у Гиппарха — 172;52,30. Точно так же произошла ошибка у [Гиппарха] в [вычислении количества] часов промежутка времени между вторым и третьим [затмениями]; при проверке оно оказалось превышающим на два часа. Это превышение у Гиппарха составляло один и две третьих часа. Избыточная дуга при проверке [составляла] 175;44 [градусов], а у Гиппарха — 175;7,30.

Вслед за этим Гиппарх таким же образом рассматривает другие три затмения и говорит, что они наблюдались в Александрии. При первой проверке Птолемей нашел, что промежуток времени между первым и вторым [затмениями] есть сто семьдесят восемь суток и шесть с половиной и одной третью равноденственного часа, градусы движения Солнца 180;11. У Гиппарха промежуток времени есть сто семьдесят восемь суток и шесть равноденственных часов, градусы [Солнца] 180;21. При проверке Птолемей нашел, что промежуток времени между вторым и третьим [затмениями] есть сто семьдесят шесть суток и две третьих часа, градусы избыточной дуги 18;55. У Гиппарха промежуток времени есть сто семьдесят шесть суток и один с одной третью равноденственного часа, градусы 168; 33. Вот это причина той ошибки, которая допущена [Гиппархом].

Комментарии

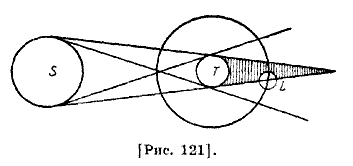
124. Четвертая книга «Альмагеста» Птолемея состоит из следующих глав:

На каких наблюдениях следует строить теорию Луны.

О периодах лунных движений.

О частных значениях средних движений Луны.

Таблица средних движений Луны.

О том, что при простой гипотезе о движении Луны, будет ли она гипотезой эксцентра или эпицикла, видимые явления будут одними и теми же.

Определение первого и простого неравенства движения Луны.

Об исправлении значений долготы и аномалии Луны.

Об эпохе равномерных движений Луны по долготе и аномалии.

Об исправлении средних движений Луны по широте и об их эпохе.

Таблица первого или простого неравенства Луны.

О том, что разница в принятой Гиппархом величине лунного неравенства получается не от различия сделанных предположений, а вследствие вычисления.

125. Лунные затмения происходят во время прохождения Луны через земную тень, иначе говоря, в то время, когда Земля становится между Луной и Солнцем, а солнечные — во время прохождения Луны по диску Солнца. Затмение Луны происходит следующим образом: пусть S — Солнце, Τ — земля, L — Луна [рис. 121]. Поскольку затмение происходит при попадании Луны в конус земной тени, то лунное затмение видно совершенно одинаково на всем земном полушарии, обращенном к Луне, и для всех точек Земли начинается в один и тот же момент.

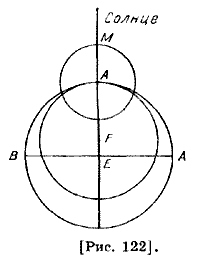
По местным часам каждой точки Земли этот момент будет находиться в разное время суток в зависимости от долготы местности, что и лежит в основе определения разности долгот с помощью наблюдения лунных затмений. Лунное затмение наступит при условии, если Луна находится в точке эклиптики, диаметрально противоположной положению Солнца. Этим и объясняется то, что данные о положении Солнца и Луны, получаемые в момент лунного затмения, более точны, чем результаты измерений с помощью инструментов, дающих менее точный результат вследствие параллактического смещения Луны.

126. В этом параграфе рассуждение аль-Фараби как по содержанию, так и по объему значительно отличается от соответствующей главы «О периодах лунных движений» «Альмагеста». Для сравнения считаем необходимым привести полный текст этой главы.

«Этого краткого изложения вполне достаточно для того, чтобы мы видели, по каким наблюдениям следует вообще определять все необходимое для теории движения Луны. Попробуем теперь изложить, каким методом древние пользовались, чтобы представить движение Луны, а также какой метод и мы сами считаем полезным для установления гипотез, наиболее соответствующих наблюдениям.

Так как нам кажется, что Луна неравномерно как по широте, так и по долготе, и не всегда в одинаковое время проходит круг через середины зодиакальных созвездий и совершает возвращение к той же широте, то без определения времени, необходимого для восстановления ее неравенств, было бы невозможно найти и другие ее периоды. Согласно произведенным подробным наблюдениям она имеет наибольшие, наименьшие и средние движения безразлично во всех частях Зодиака. Точно так же во всех частях Зодиака она бывает и самой северной, и самой южной, и находящейся на самом круге, проходящем через середины зодиакальных созвездий; поэтому, естественно, что древние математики старались найти некоторый промежуток времени, в течение которого Луна всегда совершала бы одинаковое движение по долготе, так как только по истечении этого промежутка могло бы произойти восстановление неравенства. По изложенным выше причинам, сопоставляя наблюдения лунных затмений, они смотрели, за какое количество месяцев пройденное по долготе расстояние будет всегда равным таким же расстояниям за одинаковое количество месяцев и будет содержать равные количества целых оборотов или с добавлением каких-нибудь равных дуг. Более древние вообще считали, что этот промежуток времени содержит 6585 дней с одной третью. В течение этого промежутка времени они видели, что примерно совершается 223 месячных обращения, 239 возвращений аномалии, 242 возвращения к той же широте, 241 оборот по долготе и что, кроме того, Солнце в течение этого промежутка к своим 18 круговым обращениям добавляет еще 10 градусов и две трети, если относить все возвращения к неподвижным звездам. Это время они назвали «периодическим», как первым возвращающим в исходное состояние почти все движения. Для получения целого числа дней они утроили эти 6585 1/3 дней и получили число дней, равное 19 756, которое они назвали экселигмом. Утраивая и остальные числа, они получили 669 месяцев, 717 восстановлений аномалии, 726 возвращений к той же широте, 723 оборота по долготе и, кроме того, 32 градуса, которые Солнце добавляет к 54 своим полным обращениям.

Однако Гиппарх на основании халдейских и собственных наблюдений показал, что все это не совсем точно. Действительно, на основании изложенных им наблюдений он показывает, что первое число дней, по истечении которых время затмений делает полный цикл в одинаковое число месяцев и в одинаковых движениях, равно 126 007 дням с одним равноденственным часом; в течение этого времени он находит 4267 месяцев, 4573 полных возвращений аномалии, 4612 обращений по Зодиаку без 7,5 градуса, которых недостает Солнцу для совершения 345 полных оборотов по отношению к неподвижным звездам. Он нашел, что средняя продолжительность месяца, получаемая делением приведенного числа на 4267 месяцев, будет приблизительно содержать 29; 31, 50, 8, 20 дней. В течение этого промежутка от одного лунного затмения до другого соответствующего будут пройдены одинаковые расстояния; таким образом, становится ясно, что неравенство тоже восстанавливается, так как этот промежуток времени всегда содержит такое же число месяцев, и что к одинаковым 4611 обращениям по долготе прибавляются равные дуги в 352;5 градуса, как требуют времена соединений с солнцем.

Если искать не число месяцев между соответствующими лунными затмениями, а только от одного полнолуния или новолуния до такого же соединения, то время возвращения неравенства оказалось бы меньшим, и если взять только их общий делитель — семнадцатую часть, получился бы 251 месяц и 269 восстановлений аномалии. Однако указанное время не может дать целое число возвращений к той же широте; действительно, возвращение затмений, по-видимому, сохраняет только равенство периодов по времени и по долготе, но не по величине и одинаковости затмений, по которым определяется широта.

Найдя предварительно время возвращения неравенства, Гиппарх опять стал сравнивать, промежутки времени между месяцами, имеющими крайние затмения совершенно одинаковые как по величине, так и по продолжительности, для которых не имеется никакого различия в аномалии, так что вследствие этого получалось и возвращение к той же широте; он показал, что такой период содержит 5458 месяцев и 5923 возвращения к широте.

Таким методом пользовались наши предшественники для подобных исследований. То, что он не был ни простым, ни удобным, но требовал большого внимания, мы можем видеть из следующего. Если допустить, что продолжительности двух периодов равны друг другу, то это не даст нам ничего полезного, если в каждом из этих периодов не будет никакой связи или будет всегда одинаковая разница в аномалии Солнца. Если же этого не случится, то и само оно, а также Луна не сделают одинаковых обращений в равные промежутки времени. Действительно, если, например, каждый из сравниваемых промежутков кроме целых и равных друг другу годов будет содержать половину продолжительности года, то Солнце, двигаясь в течение этого времени в первом промежутке от среднего положения в Рыбах, а во втором — от среднего положения в Деве, пройдет в первом промежутке расстояние приблизительно на 4 и три четверти градуса меньше полуокружности, а во втором на столько же больше полуокружности, таким образом, и Луна в равные времена пройдет в первом промежутке кроме целых кругов еще 175 с четвертью, а во втором — 184 с четвертью градусов. Поэтому, во-первых, следует сказать, что промежутки по отношению к Солнцу должны содержать целое число полных его обращений, нужно чтобы в одном из промежутков прибавлялась полуокружность от апогея, а в другом — от перигея, или чтобы в каждом из промежутков начало было в одном и том же месте, или чтобы для первого затмения в одном промежутке и второго в другом получались с обеих сторон одинаковые расстояния от перигея и апогея. Только при таких условиях в каждом промежутке или совсем не получится разницы в аномалии, или разница будет совершенно одинаковой, так что добавляемые дуги окажутся равными или между собой или между собой и дугами равномерного движения.

Мы полагаем, что подобным же образом следует отнестись к движениям Луны. Действительно, если на это не обратить внимания, то окажется, что Луна часто может проходить равные дуги по долготе и в одинаковые времена без полного восстановления ее неравенства. Получится движение с одинаково увеличивающейся или уменьшающейся скоростью, но движение не будет заканчиваться с той же скоростью при условии : если в одном промежутке Луна начнет движение с наибольшей скоростью и закончит с наименьшей, а в другом начнет с наименьшей и закончит с наибольшей, если в обоих промежутках места с первой скоростью одного и последней скоростью другого были равноотстоящими от одного и того же места с наименьшей или наибольшей скоростью. В каждом из этих случаев или не будет никакой разницы в неравенстве, или же разница будет одной и той же, и вследствие этого получатся по долготе одинаковые дуги, но неравенство никогда не будет восстановленным. Следовательно, в выбираемых промежутках не должно иметь места ни одно из этих явлений, если нужно, чтобы они содержали период восстановления неравенства. Наоборот, нам нужно выбирать промежутки, которые возможно лучше могут показать неравенство, если они не содержат целых периодов восстановления неравенства и начинают движение от мест с различными скоростями по величине или по потенции. По величине, если в одном промежутке движение начнется с наименьшей скоростью и не закончится наибольшей, а в другом когда начнется с наибольшей и не закончится на наименьшей скорости. Таким образом, получится наибольшая разница в дугах, пройденных по долготе, если будут описаны не полные круги аномалии, но с добавлением лучше всего одной или трех четвертей кругов аномалии, так как промежутки будут отличаться на удвоенную разность в неравенстве.

По потенции же, если в обоих промежутках движение начнется со средней скоростью, но не с той же самой, а именно в одном промежутке возрастающей, а в другом — убывающей, приращения долгот будут больше всего различаться между собой, если до восстановления неравенства опять будет недоставать одной или трех четвертей круга аномалии, так что получается двойная разница в неравенстве, а для полукруга — четверная. Мы видим, что вследствие этого и Гиппарх, проявляя величайшую осторожность при выборе промежутков в таком исследовании, для Луны пользовался двумя промежутками, из которых в одном движение начиналось с точки с наибольшей скоростью и не заканчивалось в точке с наименьшей, а в другом движение начиналось с точки с наименьшей скоростью, но не заканчивалось в точке с наибольшей; он также исправлял разницу, получающуюся от солнечного неравенства, хотя она была и наибольшей и составляла приблизительно ¹/₄ двенадцатой части Зодиака, причем в обоих промежутках она не была ни той же самой, ни производящей ту же разницу в неравенстве или в добавлении к числу описанных Солнцем полных кругов.

Мы говорим это не для того, чтобы оспаривать предложенный метод получения периодических восстановлений, но чтобы настоятельно подчеркнуть, что при настоящем внимании и соответствующем вычислении можно исправить предложенный способ; если же опустить какую-нибудь из изложенных характерных особенностей, то можно очень сильно ошибиться в искомом определении; я хочу показать также, насколько трудно получить точное наличие всех этих необходимых условий, даже если очень умно сделать выбор соответствующих наблюдений.

Таким образом, для указанных периодических возвращений при вычислении согласно методу, предложенному Гиппархом, оказалось, что для месяцев при наиболее точном вычислении не получалось никакой заметной разницы с истиной, но для аномалии и широты наблюдалась очень заметная ошибка, что мы и выяснили при помощи наиболее простых и удобных методов, употребляющихся для подобного исследования, как мы сейчас покажем при определении величины лунного неравенства. Сначала, что будет очень полезно для дальнейшего, мы дадим отдельные средние движения по долготе, широте и аномалии, в соответствии с указанными выше временами периодических возвращений, а также добавим поправки, получающиеся после исправления тем методом, который мы изложим в дальнейшем» [3, стр. 194—203].

127. Противостояние (мукабала) — случай, когда долготы двух светил отличаются на 180°, соединение (иджтима) — совпадение долгот двух светил.

128. Халдеи — семитические племена в Южной Месопотамии, образовавшие в конце 7 в. до н. э. Ново-Вавилонское государство.

129. Это так называемый синодический месяц, в течение которого Луна возвращается в прежнее положение относительно Солнца.

130. Если λ'_L — средняя долгота Луны, λ'_S — средняя долгота солнца, то разность λ'_L —λ'_S называют средней суточной величиной элонгации Луны (от латинского слова elangotio — «удаление»).

131. Египетский год содержит ровно 365 суток и поэтому называется равным (равновеликим) в отличие от римского, в котором бывает 365 и 366 суток.

132. Эта таблица приведена в приложениях (таблица 7).

133. Здесь квадратура (тарби') и гексагональный аспект (тасдис), тригиональный аспект (таслис) — расположение светил в знаках Зодиака, имеющих расстояния соответственно 90, 60 и 120°.

134. Первое неравенство в движении Луны объясняется с помощью эпициклической гипотезы [рис. 122]. Центр эпицикла А по концентрическому кругу и Луна Μ по эпициклу двигались в противоположные стороны (центр А — против часовой стрелки, а Луна — по часовой стрелке) и совершали в абсолютном движении полный оборот относительно прямой АЕС, все время проходящей через Солнце в течение одного синодического месяца (29,5 дня); тогда движение Луны казалось наиболее медленным в точке Μ эпицикла и наиболее быстрым в точке N.

От сложения двух вращений в противоположные стороны получилось движение Луны вокруг Земли по эксцентрическому кругу, центр F которого все время находится на прямой, соединяющей центр Ε Земли с Солнцем [9, стр. 599].

135. Эта предпосылка и ее следствие отсутствуют в «Альмагесте» и являются собственным добавлением аль-Фараби. Они служат теоретико-методической базой в определении положения Луны и ее аномалии через наблюдение в двух группах по три затмения, приведенной в дальнейшем Птолемеем.

136. По мнению О. Нейгебауера, здесь мы имеем оригинальный пример применения тригонометрии к решению астрономической задачи, где описан математический метод определения длины радиуса эпицикла Луны и положения апогея. Эта задача представляет собой простейший случай более общей задачи определения параметров орбиты на основании ряда наблюденных положений. Она тесно связана также с важной геодезической задачей — определением положения наблюдателя по отношению к трем данным точкам [4, стр. 201—204].

Эта задача в данном случае такова: по известным скоростям изменений аномалии γ и средней долготы λ центра эпицикла определить r и момент, когда Луна имеет минимальную скорость, т. е. находится в апогее эпицикла.

В тех единицах, в которых радиус деферента равен 60, радиус эпицикла был найден равным 5;15.

137. Набонассар (у аль-Фараби Бухтунассар) — вавилонский царь, царствовал в 747—733 гг: до н. э. Начало эры Набонассара, упоминавшейся в «Альмагесте», — 26 февраля 747 г. до н. э., день вступления Набонассара на престол.

138. Узел — «'укда» — точка пересечения эклиптики с орбитой Луны.

139. Здесь аль-Фараби указывает, что при определении движения Луны по широте по ее затмениям надо учитывать, что при одной и той же величине широты величина тени Луны может быть различной. Она зависит от расстояния Луны от апогея эпицикла (если придерживаться эпициклической гипотезы), то есть от расстояния Луны от Земли. Тень наибольшая при положении Луны в высшей точке эпицикла (когда Луна ближе всего к Земле) и уменьшается по мере движения Луны по эпициклу к его высшей точке (причем учитывается перемещение узла лунной орбиты). Таким образом, для того чтобы судить об истинном возвращении по широте, необходимо, чтобы для двух затмений величина затмений была одной и той же и расстояния Луны от апогея эпицикла были бы одинаковыми.

140. Названия восходящего и нисходящего узлов Луны — «голова» (рас) и «хвост» (занаб) связаны с древним суеверием о голове и хвосте Дракона, живущего в узлах лунной орбиты и пожирающего Солнце во время затмений, которые могут произойти лишь в узлах.

141. Палец (исба') — ок. 2 см.

142. Аль-Фараби объясняет метод Птолемея вычисления движения Луны по широте. Если известны данные наблюдений двух затмений, разделенных большим промежутком времени, и были равны величины затмения для равных расстояний Луны от высших точек их эпициклов, то их широты также равны; следовательно, по средним фазам затмений можно получить эпоху периодических изменений широты, т. е. за промежуток времени между указанными затмениями движение Луны содержит целое число оборотов по широте. Если же Луна в обоих затмениях находится на различном расстоянии от высшей точки эпицикла, это дает возможность определить среднее движение Луны по широте за указанный промежуток времени, а следовательно, и среднее годовое, месячное и суточное движение Луны по долготе.

143. Положение Луны в произвольный момент времени определяется его средней долготой λ («средним движением»), истинной долготой λ' («истинным движением»), уравнением Θ= [λ'—λ] и аномалией α [рис. 123].

144. Эта таблица приведена в приложениях (таблица 8).