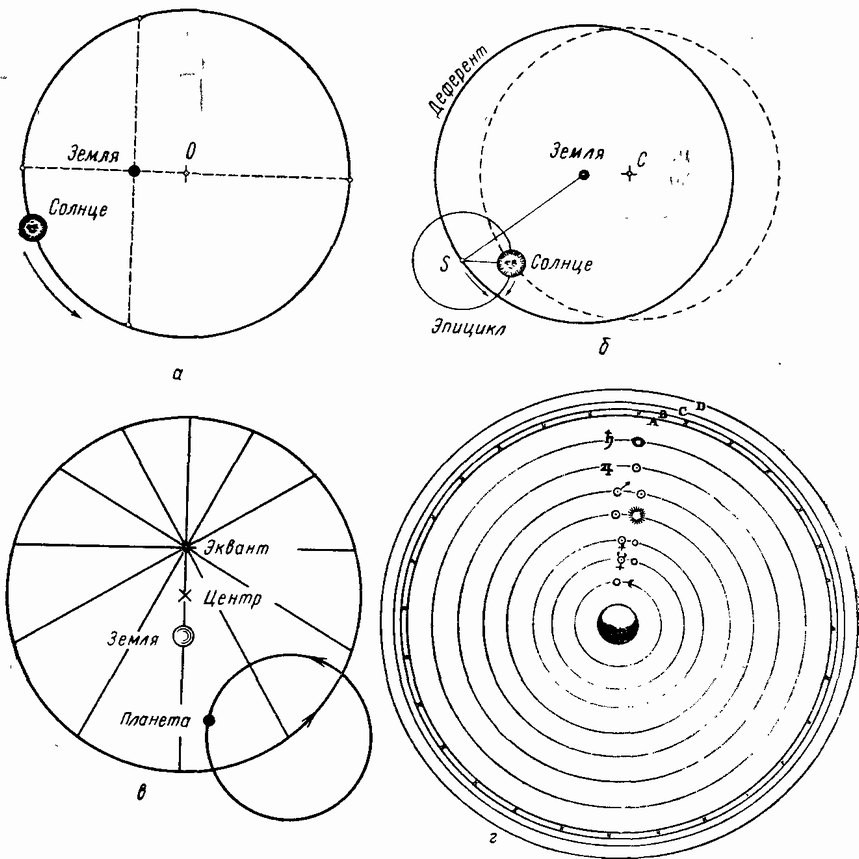
§ 1. Создание основ математической и точной наблюдательной астрономии. Аполлоний Пергский, Гиппарх

Начиная с III в. до н. э. в Греции все более распространялись и усваивались астрономические и математические достижения Вавилона. Греческая наблюдательная астрономия достигла точности вавилонской. В практику вошли (возможно, вавилонские) угломерные инструменты с измерительными кругами, разделенными на градусы и минуты. Все это в сочетании с геометрическим направлением греческой математики создало благоприятные условия для нового прогресса математической астрономии.

Этому способствовало создание новых математических методов и целых областей математики. Аристарх Самосский начал применять в астрономии теорию хорд — предшественницу сферической тригонометрии. Его современник математик Аполлоний Пергский разработал около 230 г. до н. э. новый геометрический метод описания неравномерных периодических движений. Он показал, что такое движение может быть представлено как сумма двух равномерных круговых: по одной окружности (деферент, по греч. — несущий) равномерно движется центр вторичной окружности (эпицикл), по которой в свою очередь равномерно движется исследуемое тело.

Применительно к астрономии этот метод впервые развил Гиппарх (ок. 190/180—125), величайший древнегреческий астроном эпохи эллинизма. Он был родом из Никеи (ныне Турция), но жил и работал на острове Родос. С его именем связано начало новой эпохи в развитии точной наблюдательной и теоретической астрономии, так как он выдвинул требование: строить точную математическую теорию движения небесных тел только на основе предельно точных данных наблюдений. Определив за период 162—128 гг. моменты около десяти равноденствий и сравнив их с данными Аристарха (ок. 280 г. до н. э.), Гиппарх уточнил длину тропического года, уменьшив предшествовавший ему результат Каллиппа (365 1/4) на 1/300 дня. Он уточнил также данные Каллиппа о продолжительности сезонов (см. табл.), получил параметры эксцентрической орбиты видимого движения Солнца.

Гиппарх первым обратил внимание на различие длины тропического и сидерического годов (на 15 мин, в действительности — 20 мин). За период 146—135 гг. он наблюдал также несколько лунных затмений.

Используя эти и другие наблюдения и математический аппарат Аполлония Пергского, Гиппарх построил первую теорию неравномерного движения Солнца и Луны. Новый, геометрический метод Гиппарха качественно отличался от моделирования движений небесных тел в эпоху Евдокса — Аристотеля. Он полностью отрывал математическую теорию движения от объемных механических моделей, которые, во-первых, были трудны для расчетов, а во-вторых, невольно воспринимались как воспроизведение реального устройства мира. Теория Гиппарха не «демонстрировала» движения, а устанавливала их количественные характеристики. Он нашел, что суммарное движение по эпициклу и деференту тождественно более наглядному движению по эксцентрику в том случае, когда угловые скорости двух первых равны, а направления противоположны. Представляя видимое движение Солнца с помощью эксцентрика, Гиппарх показал, что наблюдатель действительно должен будет видеть его неравномерным, более быстрым с той стороны, в которую сдвинуто место наблюдателя от центра круга. В этой модели впервые появились элементы, определяющие орбиту небесного тела (хотя еще и геоцентрическую): апогей и перигей, эксцентриситет, которые Гиппарх и оценил (получил эксцентриситет солнечного пути 1/24 и долготу апогея 65°30′) (рис. 11, а).

Данные о продолжительности сезонов

По собственным и некоторым тщательно проверенным вавилонским наблюдениям лунных затмений Гиппарх построил теорию движения Луны, также использовав образ эксцентрика, и существенно уточнил различные периоды его (месяцы — драконический, аномалистический и т. д.). Вместо сароса он ввел более точный цикл почти в 345 лет (126 007 дней + 1 час), который охватывал огромные целые числа различных месяцев (от 4267 до 4612). Это позволило ему уточнить, например, синодический и сидерический месяцы, получив величины, отличающиеся от современных нам данных всего на 0,4 с и 1,7 с соответственно.

Составленные Гиппархом таблицы солнечных и лунных затмении позволяли предсказывать их с неслыханной по тому времени точностью — в пределах 1—2 часов. По наблюдениям солнечных и лунных затмений он оценил параллакс Луны и относительные расстояния Луны и Солнца в радиусах Земли (59 и 1200 соответственно). Он усовершенствовал цикл повторения лунных фаз и дней солнечного года: ввел учетверенный без одного дня цикл Каллиппа, что, однако, не нашло практического применения. Гиппарху также принадлежит введение географических широты и долготы.

Рис. 11. Геоцентрические системы мира (геометрические модели): а) модель движения Солнца по эксцентрику (Гиппарх), б) принцип эпициклического движения планет (Птолемей), в) эквант Птолемея, г) система мира Птолемея

За теорию планет Гиппарх не брался сознательно, считая имевшийся наблюдательный материал недостаточным. Но он наблюдал планеты и, в частности, уточнил средние периоды их обращения, что использовал Птолемей.

Сравнение результатов наблюдений разных эпох (что стало в дальнейшем характерным для астрономии) привело Гиппарха к его наиболее знаменитому результату — открытию прецессии. То, что Солнце возвращается к одному и тому же положению среди звезд за период, больший, чем возвращение его к одному и тому же равноденствию, заметили уже вавилонские астрономы. Но при своем чисто феноменологическом подходе к наблюдению неба они не пытались это объяснить. Гиппарх исследовал вопрос в специальном сочинении «Об изменении солнцестояний и равноденствий» и отметил, что яркая звезда Спика (α Девы), к которой Солнце подходило незадолго до дня осеннего равноденствия, во времена Тимохариса (примерно за 169 лет до Гиппарха), «опережала» точку равноденствия на 8°, а по наблюдениям Гиппарха — лишь на 6°. А так как звезды не двигались друг относительно друга (о чем свидетельствовала неизменность формы созвездий), Гиппарх заключил, что движутся — «отступают» — навстречу Солнцу точки равноденствий и солнцестояний. Первая оценка этой величины Гиппархом была довольно точной: 2°/169 лет=47″ в год (действительная величина 50,3″). В дальнейшем Гиппарх подтвердил эффект по 18 ярким звездам, сравнивая их склонения по Тимохарису и по собственным измерениям. Но оценку смещения равноденствий в другой работе «О длине года» Гиппарх дал менее определенную («по крайней мере на 3° за 300 лет», в смысле «не менее»). Эффект получил наименование предварения (лат. — прецессия) равноденствий.

И еще одну принципиально новую черту звездной Вселенной открыл Гиппарх. Появившаяся в 134 г. до н. э. в созвездии Скорпиона новая яркая звезда (которую китайцы лишь старательно зафиксировали) навела его на мысль, что изменения могут происходить и в сфере звезд! Чтобы легче замечать такие изменения, он составил каталог положений на небе около 850 звезд и впервые разбил все видимые звезды на шесть классов по их блеску, назвав самые яркие звездами первой величины (он связывал это с геометрическими размерами их).