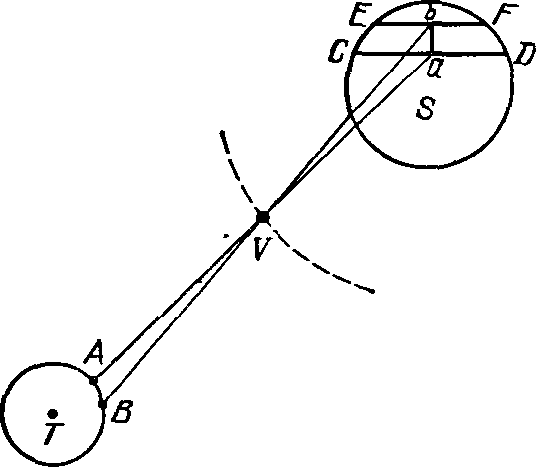
Измерить и взвесить!

Спор о фигуре Земли. Уже упоминавшийся выше Жан Рише, находясь в Кайенне (географическая широта φ = +5°), обратил внимание на то, что маятник фиксированной длины качается медленнее, чем в Париже. Отсюда следовало, что ускорение силы тяжести на экваторе меньше, чем в высоких широтах. Было найдено и объяснение этому явлению: оно обусловлено действием центробежной силы, возникающей при вращении Земли. Отсюда оставался один шаг до заключения, что по этой причине Земля «чуточку» сплюснута у полюсов. Такое заключение сделал Гюйгенс около 1683 г. и опубликовал его в 1687 г., оценив величину сплюснутости в 1/578.

Независимо от Гюйгенса и даже несколько раньше к тому же выводу пришел и Ньютон. В предположении об однородности Земли, учитывая взаимное притяжение всех составляющих ее материальных частиц, Ньютон нашел, что отношение полярного радиуса Земли к экваториальному составляет 229/230, так что сплюснутость ее равна 1/230 (современное значение 1/298,3). Ньютон показал также, что из-за отклонения Земли от сферичности под действием притяжения Солнца и Луны происходит прецессионное движение земной оси, и подсчитал величину прецессии 50″ в год (к тому же он показал, что это прецессионное движение не может быть вполне равномерным, так как положение Солнца и Луны относительно плоскости земного экватора изменяется; соответствующее короткопериодическое колебание — нутация—было открыто в 1747 г. Джеймсом Брадлеем).

Тем не менее французские астрономы на основе проводившихся в течение многих лет измерений длины дуги меридиана пришли к выводу, что длина 1° меридиана уменьшается к северу. Напрашивался вывод, что Земля должна быть вытянута у полюсов. Поэтому в среде французских ученых, где господствовала вихревая теория Декарта, к теории Ньютона относились скептически. В своих «Письмах из Лондона об английском» Вольтер в 1730 г. писал: «Француз, который попадает в Лондон, обнаруживает, что все совершенно изменилось в философии... В Париже вы видели вселенную, наполненную круговыми вихрями из тончайшей материи, в Лондоне вы ничего этого не видите... В Париже Земле придают форму дыни, в Лондоне она сплюснута у полюсов»...

Кстати, в 1733 г. Вольтер в трактате «Элементы философии Ньютона» изложил в популярной форме ньютонову теорию света и закон всемирного тяготения. Он же был инициатором перевода «Начал» на французский язык.

Между тем Парижская Академия наук приняла решение для измерения длины дуги меридиана послать экспедицию в северную часть Перу (теперь Эквадор), а также в Лапландию. К 1740 г. уже стало ясно, что с увеличением широты длина дуги, соответствующей 1° меридиана, возрастает. Это решило спор в пользу идей Ньютона и в значительной мере содействовало их распространению во Франции и в Европе в целом.

Измерения параллакса Солнца. Одной из важнейших задач, стоявших перед астрономами еще при жизни Ньютона, было уточнение расстояния от Земли до Солнца. Кроме уже упоминавшегося метода наблюдений Марса в противостоянии с двух точек Земли они решили использовать явление прохождения Венеры по диску Солнца. Впервые указал на такую возможность Галлей, который, находясь на острове св. Елены в 1676 г., наблюдал прохождение Меркурия по диску Солнца. Регистрируя моменты вступления и схождения планеты с диска Солнца, Галлей получил, однако, для параллакса Солнца явно неудовлетворительный результат 45″ (истинное значение 8,79″). Галлей сделал вывод, что точность метода будет намного выше, если наблюдать прохождение по диску Солнца Венеры. «Это наблюдение такого рода, которое одно только и может дать в следующем веке расстояние от Солнца до Земли, а именно когда Венера будет находиться перед солнечным диском 26 мая 1761 г., тогда параллакс Венеры будет почти втрое больше солнечного, наблюдения будут удобными и все, что можно получить при этом, будет легко осуществимо», писал он в 1691 г.

Очевидно, что если бы плоскость орбиты Венеры совпадала с плоскостью эклиптики, то прохождение Венеры по диску Солнца наблюдалось бы через каждые 584 дня в нижнем соединении планеты с Солнцем. Однако плоскость орбиты Венеры наклонена к эклиптике под углом 3,39°, и поэтому упомянутое явление имеет место лишь в случае, когда Венера в нижнем соединении находится вблизи узла своей орбиты. А поскольку эти узлы медленно передвигаются относительно точки весеннего равноденствия, то прохождения Венеры по диску Солнца происходят с интервалами 121,5; 8; 105,5 и 8 лет: в июне 1761 и 1769, в декабре 1874 и 1882 и в будущем — в 2004 и 2012, а также в 2117 и 2125 годах.

Рис. 47. Прохождение Венеры по диску Солнца, наблюдаемое из двух пунктов Земли

Задача заключается в том, чтобы зафиксировать моменты «касания» дисков Солнца и планеты и их «отрыва». Разность этих моментов дает длительность прохождения Венеры по диску Солнца t_A (t_A достигает 7 часов, если планета проходит через центр диска) для наблюдателя, находящегося в определенном пункте A с известными географическими координатами. Если же пункты A и B расположены на различных широтах, то для наблюдателя в пункте A Венера пройдет по хорде CD, а для наблюдателя в пункте B — по линии EF (рис. 47). При прохождении Венеры по краю солнечного диска разница времени t_A − t_B может достигнуть половины часа. Поскольку же ∠aVb = ∠AVB, по известному расстоянию AB нетрудно определить расстояние от Земли до Венеры, а следовательно, и до Солнца.

Для регистрации моментов явления были организованы многочисленные экспедиции в Индию, на мыс Доброй Надежды в Африку, на остров Святой Елены, а в России — в г. Тобольск, кроме того, астрономы проводили наблюдения «дома». Еще организованнее были наблюдения 1769 г. В итоге оказалось, что первые не отличались желаемой точностью: ведь географическая долгота многих пунктов была известна лишь приближенно или неизвестна совсем, а ее определение по наблюдениям затмений спутников Юпитера проводилось с большими ошибками. Но в 1769 г. в тот же день произошло частное солнечное затмение, благодаря чему определение координат существенно облегчилось. В итоге параллакс Солнца по наблюдениям 1761 г. «колебался» между 8″ и 10″, по данным 1769 г. — между 8″ и 9″. Тщательная обработка этих последних данных, законченная в 1835 г., привела к величине 8,57″. Это соответствует расстоянию от Земли до Солнца в 153,5 млн км, которое и было принято на многие десятилетия.

Прохождение Венеры по диску Солнца в 1761 г. наблюдал и выдающийся русский ученый-энциклопедист М.В. Ломоносов (1711—1765). Несколько недель спустя он опубликовал брошюру «Явление Венеры на Солнце, наблюденное в Санктпетербургской Императорской Академии наук Мая 26 дня 1761 года». В ней была подробно описана картина деформации края диска Солнца при приближении к нему Венеры (рис. 48), а также светлая каемка вокруг планеты. Из этого Ломоносов сделал вывод, что планета Венера окружена «знатной воздушной атмосферой, таковой (лишь бы не большею), какова обливается около нашего шара земного». Так было доказано физическое сходство одной из планет с Землей. Ломоносов сам же высказал предположение о возможности существования жизни на этой планете... К брошюре была приложена статья в защиту гелиоцентрического учения, написанная со стихотворными вставками.

Рис. 48. Рисунок М.В. Ломоносова к описанию открытия им атмосферы на Венере 26 мая 1761 г.

Как взвесить Солнце? Не менее важной задачей, стоявшей перед астрономами XVIII в., было определение масс тел Солнечной системы не в относительных (это сделал Ньютон), а в абсолютных единицах. И с этой задачей они справились блестяще.

Напомним, что третий закон Кеплера можно представить в виде

T²/a³ = (4π²);/(GM),

где G — постоянная тяготения, M — масса «силового центра», T — сидерический период обращения материальной точки m вокруг этого центра (Земли вокруг Солнца, Луны вокруг Земли и т. д.) по эллиптической орбите, большая полуось которой a. Используя эту формулу сначала для Земли, обращающейся вокруг Солнца, и еще раз — для Луны, движущейся вокруг Земли, и разделив первое выражение на второе, получаем массу Солнца, выраженную в массах Земли: M_☉ = 330 000 M_⊕. Для определения последней достаточно установить ее среднюю плотность ρ̅_⊕. Ньютон оценил ее, исходя из таких соображений: «Поскольку обычные верхние слои Земли имеют плотность приблизительно вдвое большую, нежели вода, а немного глубже, в рудниках, оказываются приблизительно в три, четыре и даже 5 раз тяжелее, то правдоподобно, что все количество вещества Земли приблизительно в 5 или 6 раз больше того, как если бы она состояла только лишь из воды». Это предположение, как оказалось позже, было очень точным, однако его необходимо было подтвердить непосредственными измерениями.

В 1749 г. французские астрономы Пьер Бугер (1698—1758) и Шарль Мари ла Кондамин (1701—1774), проводя наблюдения в Перу вблизи горы Чимборасо, обнаружили, что отвес (маятник) отклоняется от вертикального положения на 7—8″. Это натолкнуло их на мысль, что, пользуясь маятником, можно оценить массу Земли, сравнивая ее с массой горы, которую нетрудно определить. Но их попытка тогда не увенчалась успехом.

Рис. 49. Отклонение отвеса у горного хребта

В 1774 г. английский астроном Невилл Маскелайн (1732—1811) осуществил аналогичные измерения, избрав для этого гору Шегальен в Шотландии — узкий гранитный хребет, протянувшийся с запада на восток. Измерения зенитного расстояния полюса проводились в двух точках, расположенных на одном меридиане, один из пунктов был севернее, второй южнее хребта. Если бы между ними не было горы, то заданному между ними расстоянию в 1330 м соответствовала бы разность зенитных расстояний полюса мира 43″. Но после окончания наблюдений и их сопоставления оказалось, что это расстояние составляет 54,8″: отвес отклонялся от вертикали на 5,9″ (рис. 49). Предположив, что и масса горы, и масса Земли сконцентрированы в их центрах масс, можно было после некоторых вычислений определить, что плотность Земли в 1,8 раза превышает плотность горы. Следовательно, при средней плотности горы (гранита) 2,6 г/см³ было найдено ρ̅_⊕ = 4,7 г/см³.

В 1798 г. Генри Кавендиш (1731—1810) «заменил» гору парой свинцовых шаров весом по 158 кг каждый. К этим массам притягивались пробные массы весом по 729 г, подвешенные на горизонтальной деревянной палочке, закрепленной в центре масс тонкой серебряной нитью (рис. 50). Мерой силы притяжения в данном случае был угол, на который закручивалась нить. Таким образом Кавендиш установил, что средняя плотность Земли ρ̅_⊕ = 5,5 г/см³ и что масса Земли M_⊕ = 5,98·10²⁷ г. А так как из третьего закона Кеплера следует, что масса Солнца в 330 тысяч раз больше, то тем самым M_☉ = 2·10³³ г. Так удалось «взвесить» Солнце в лаборатории при помощи деревянной (из пихты) палочки...

Рис. 50. Опыт Кавендиша

Особенности движения Луны. Еще в 1514 г. Иоганн Вернер из Нюрнберга в комментариях к переведенной им «Географии» Птолемея предложил для определения долгот измерять расстояния от центра Луны до избранных звезд из зодиакальных созвездий. В самом деле, передвигаясь каждый час на 0,5° — на величину своего диаметра — Луна как бы отсчитывает время на циферблате больших небесных часов. И штурману, отправляющемуся и далекое плавание, следует лишь запастись таблицами положений Луны среди звезд, рассчитанных на определенное время вперед, и решать задачу в такой очевидной последовательности: 1) измерить угловое расстояние центра диска Луны от «опорной» звезды, 2) учесть рефракцию и параллакс, т. е. исправить наблюдение так, как будто оно проведено из центра Земли, 3) установить местное время наблюдения путем измерения высоты Солнца или звезды и проведения расчетов по формулам сферической тригонометрии, 4) установить путем интерполяции табличных данных время нулевого меридиана на момент наблюдения и, наконец, 5) найти разность местного времени и времени нулевого меридиана, которая и будет долготой места наблюдения, выраженной в часовой мере.

Однако, чтобы этот метод давал практически полезные результаты, необходимо было проводить расчеты таблиц положений Луны с точностью буквально до секунд дуги. Ведь погрешность в определении положения Луны в Г приводила к тому, что координаты судна в океане по долготе находились с погрешностью... до 27 морских миль (т. е. до 50 км).

Поэтому на долгие годы разработка теории движения Луны оставалась в числе важнейших проблем многих выдающихся ученых и обсерваторий, в том числе Гринвичской, где, например, Эдмонд Галлей проводил наблюдения Луны непрерывно на протяжении 18 лет. В принципе было ясно, что неравенства («возмущения») в движении Луны обусловлены притяжением Солнца, но, как отмечал А. Паннекук, «теория не могла определить точное количество возмущений, хотя ей удалось показать, какие возмущения должны проявляться и с каким периодом, а также как они зависят от Солнца, узлов и афелиев»...

Вот несколько эпизодов из этой поистине героической эпопеи. В 1746 г. французский астроном Алексис Клод Клеро (1713—1765) обнаружил, что большая ось лунной орбиты согласно теории вращается со скоростью 20° в год, тогда как наблюдения указывали на вдвое большую величину. Клеро даже предпринял попытку «уточнить» закон всемирного тяготения, представив его в виде F = (Gm₁m₂/r²)(1 + α/rⁿ), где α — постоянная величина, n = 1 или 2. Позже, конечно, необходимость в ней отпала...

Большую роль в разработке теории движения Луны сыграли работы Леонарда Эйлера. Этот выдающийся уче-ный родился в Базеле (Швейцария), учился в Базельском университете. В 20 лет, в 1727 г., он был пригашен для работы в Петербургскую Академию наук. В 1741 г., сохраняя с ней тесные контакты, он на 25 лет переехал в Берлин, после чего возвратился в Россию, где в 1783 г. «перестал жить и вычислять». В 1735 г. Эйлер ослеп на один глаз, но это, как отмечают его биографы, вызвало у Эйлера лишь замечание, что «теперь он меньше будет отвлекаться от математики». В 1766 г. он ослеп и на другой глаз, но и это мало повлияло на его изумительно богатую научную деятельность. В 1753 г. Эйлер опубликовал «Теорию движения Луны», которая для немецкого астронома Тобиаса Майера (1723—1762) послужила основой при составлении таблиц движения Солнца и Луны, позволявших определять долготы с точностью выше 1°. Через 11 лет, в 1766 г., Маскелайн издал «Морской альманах и астрономические эфемериды на 1767 г.», где были даны расстояния центра Луны от Солнца и от избранных звезд через каждые три часа. Именно с того момента и начался отсчет долгот от гринвичского меридиана, во всяком случае — для тех, кто пользовался этим «Морским альманахом», который издается непрерывно и по сей день. Формально же рекомендация об отсчете долгот от гринвичского меридиана была принята Международной меридианной конференцией в октябре 1884 г. Как отмечает А. Паннекук, с появлением таблиц Майера вопрос о «тонкостях» в движениях Луны для практического мореплавания был разрешен.

Однако астрономы столкнулись с другой проблемой. Еще в 1693 г. Галлей, сопоставив моменты затмений по античным и арабским источникам с теоретически рассчитанными, пришел к выводу, что период обращения Луны вокруг Земли уменьшается. Иначе говоря, происходит «вековое ускорение» Луны. Майер нашел, что величина этого ускорения составляет 9″ в сто лет. Позже, в 1770 г., Парижская Академия наук даже предложила премию за исследование, можно ли это явление объяснить, исходя из закона всемирного тяготения. Перед этой проблемой оказался бессильным и Эйлер, он высказался так: «Кажется твердо установленным с несомненной очевидностью, что вековые неравенства лунного движения не могут вызываться силами тяготения». Эйлер сделал попытку объяснить это торможение Луны сопротивлением материальной среды, заполняющей мировое пространство... Не смог объяснить его и другой выдающийся ученый — Жозеф Луи де Лагранж (1736—1813). Решить задачу взялся его соотечественник, французский астроном и математик Пьер Симон Лаплас. В 1783 г. он пришел к такому выводу: торможение Луны обусловлено действием... других планет Солнечной системы, но не прямо, а косвенно. Под их влиянием, дескать, изменяется эксцентриситет земной орбиты, и если он уменьшается, то среднее расстояние Земли от Солнца несколько увеличивается. Благодаря этому возмущающее влияние Солнца на Луну становится меньше... Лаплас путем теоретического расчета нашел величину эффекта в 10″ за столетие, и «волнение снова улеглось».

Лапласу удалось разработать теорию движения Луны, на основе которой ее положения определялись с точностью до 0,5′. Слагаемые, которыми в этой теории описывались изменения долгот апогея и узла, оказались зависящими от величины сплюснутости Земли. Еще одно слагаемое, вызывающее «параллактическое неравенство» с амплитудой около 2′, зависело от отношения расстояний Солнца и Луны от Земли. По этому поводу Лаплас писал: «Замечательно, что астроном, не покидая своей обсерватории, а лишь сравнив наблюдения Луны с данными математического анализа, может вывести точную величину и форму Земли и расстояние ее от Солнца и Луны, для чего раньше были необходимы трудные и продолжительные путешествия». И в самом деле, Лаплас, на основании данных наблюдений и пользуясь развитой им теорией, нашел сплюснутость Земли равной 1/305, а параллакс Солнца 8,6″.

При выводе выражения для истинной долготы Луны Лаплас включал члены до третьего порядка в эксцентриситете и наклоне плоскости лунной орбиты. В 1857 г. немецкий астроном Петер Андреас Ганзен (1795—1874) уточнил теорию движения Луны с учетом членов восьмого порядка. В итоге расхождение между теорией и наблюдениями за сто лет (1750—1850) не превышало 2″. Но в это время английский астроном Джон Кауч Адамс (1819—1892) убедительно показал, что Лаплас ошибся: лишь 5,7″ в ускорении Луны можно объяснить уменьшением эксцентриситета Земли. И, наконец, в 1865 г. французский астроном Шарль Эжен Делонэ (1816—1872) нашел ответ: недостающие секунды в вековом ускорении Луны — это не что иное, как результат замедления вращения Земли, обусловленного приливным трением, т. е. трением о морское дно (и слоев воды друг о друга) бегущей вслед за Луной приливной волны. Вскоре английский астроном и математик Джордж Хауэрд Дарвин (1845—1912) провел соответствующие расчеты, из которых следовало, что примерно 4 млрд лет назад Луна находилась на расстоянии около 14 тыс. км от Земли, а земные сутки тогда длились всего около 5 часов. Через несколько миллиардов лет расстояние Луны от Земли увеличится почти в полтора раза, причем период обращения Луны увеличится до 628 часов (47 современных суток) и такими же будут тогда и земные сутки. После этого, согласно Дарвину, приливное трение будет оказывать на Луну обратное действие: она будет приближаться к Земле...

И когда все, казалось, уже было учтено, Ганзен обнаружил в долготах Луны, зарегистрированных на протяжении многих десятков лет на Гринвичской обсерватории, «еще одну медленную флуктуацию», всего несколько десятков секунд. Но их ведь также чем-то следовало объяснить! Ганзен и «обвинил» в этом планету Венеру. И тут за дело взялся американский астроном Саймон Ньюком (1835—1909). Он собрал и обработал все наблюдения Луны, начиная с древнейших времен, проехал в 1871 г. по Европе и собрал из архивов все наблюдения затмений, покрытий Луною звезд и т. д. В итоге — вывод: да, действительно, между теорией и наблюдениями имеется расхождение, отклонение на 17″ за 273 года. Как отмечает А. Паннекук, на какое-то мгновенье Ньюком подошел к идее, что причина этого — не в теории и не в Луне, а... в неравномерности осевого вращения Земли. Это и было обосновано по наблюдениям планет и спутников Юпитера уже в XX в.

Современная теория движения Луны разработана американским астрономом Джорджем Уильямом Хиллом (1838—1914). На ее основе другой американский астроном Эрнест Уильям Браун (1866—1938) рассчитал таблицы движения Луны, используемые и сегодня при составлении астрономических ежегодников.