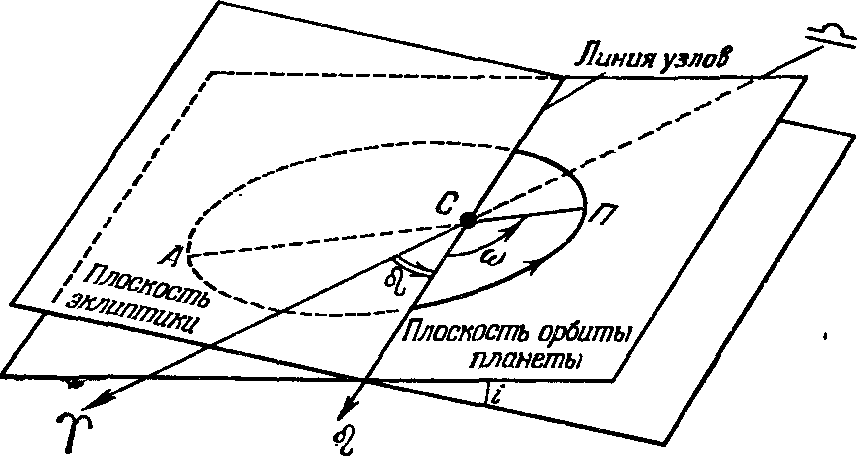
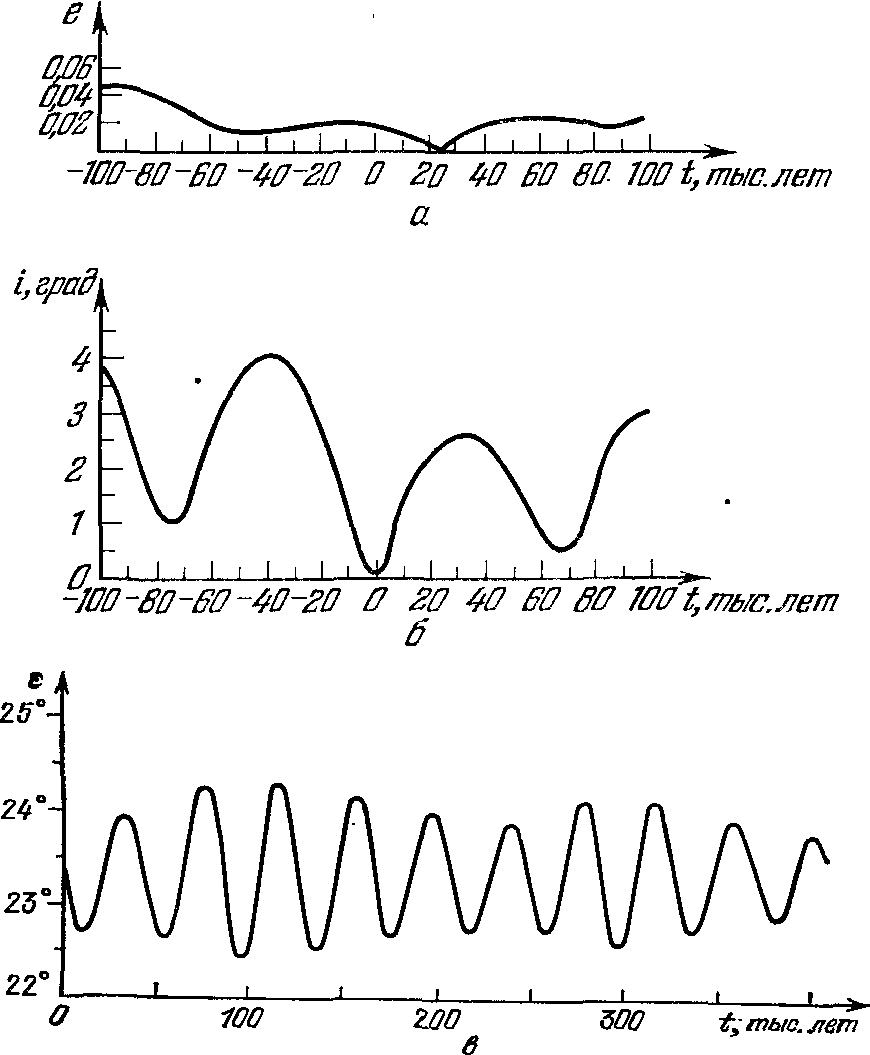
Трудная проблема устойчивости

Устойчивость планетной системы. Несколько повторяясь, напомним, что для предвычисления положения планеты на десятки дней или лет вперед (для составления ее эфемерид) необходимо знать следующие элементы ее орбиты: 1) большую полуось a, 2) эксцентриситет e; этим определяются размеры и форма орбиты. Далее, 3) наклон i плоскости орбиты к плоскости эклиптики, 4) угловое расстояние ♌ от точки весеннего равноденствия до восходящего узла, т. с. до точки, в которой планета пересекает плоскость эклиптики, двигаясь к северному полюсу мира, это — долгота восходящего узла. Тем самым определяется положение плоскости орбиты в пространстве. Кроме того, необходимо знать положение орбиты в ее плоскости, т. е. 5) угловое расстояние ω перигелия от восходящего узла, или долготу перигелия (рис. 53). И, наконец, задается 6) момент прохождения планеты через перигелий t₀. Метод определения элементов орбит по нескольким (не менее трех) наблюдениям наиболее полно разработал К. Гаусс.

Как мы уже видели, из-за взаимного притяжения планет каждая из них несколько отклоняется от движения по эллипсу, и эти отклонения называются возмущениями. Говорим так: планета в каждый момент времени движется по эллиптической орбите, однако параметры ее все время меняются. Такую орбиту принято называть варьирующей, или оскулирующей. Усилиями выдающихся математиков (Клеро, Эйлер, Лагранж, Лаплас и другие) удалось получить формулы для оценки отклонений элементов орбит от их начальных значений. Именно благодаря этому и удалось открыть Нептун и Плутон.

Рис. 53. Элементы орбит планет

И здесь неминуемо возникает такой вопрос: насколько устойчива планетная система в целом? Всегда ли возмущения элементов орбиты той или другой планеты будут оставаться небольшими? Не накапливаются ли они со временем, что в будущем могло бы привести к уходу планеты из системы или, наоборот, к ее падению на Солнце?

Уже Кеплер в 1625 г. обнаружил, что Юпитер и Сатурн уклоняются от движения по своим эллиптическим орбитам. Позже Галлей установил, что Юпитер движется ускоренно, его орбита со временем как бы уменьшается, тогда как движение Сатурна, наоборот, замедленное, его орбита становится больше. Конечно, эффект в числовом выражении был относительно невелик: от расчетных положений эти планеты за 1000 лет должны были бы отклониться соответственно на 0°57′ и 2°19′.

В попытке объяснить это явление Эйлер и начал исследование уравнении возмущенного движения планет, используя метод представления каждого из параметров орбиты планеты в виде ряда

Π = Π₀ + μΠ₁(t) + μ²Π₂(t) + ... + μⁿΠ_n(t) + ...,

где μ — масса возмущающей планеты, выраженная в массах Солнца (для Юпитера μ_J = 0,001). Если планета движется под действием только солнечного притяжения, то μ = 0. Малые добавки μΠ₁(t) называются возмущениями первого порядка, добавки μ²Π₂(t) — возмущениями второго порядка и т. д.; здесь t — время.

Как показал анализ, функции μⁿΠ_n(t) имеют сложную структуру и состоят из слагаемых трех типов: 1) μⁿA_n sin ν_nt (A_n и ν_n — постоянные), 2) μⁿB_ntⁿ (B_n — постоянная) и 3) μⁿO_ntⁿ sin ν_nt (C_n и ν_n — постоянные). Члены первого типа называются периодическими неравенствами, второго типа — вековыми неравенствами и третьего типа — смешанными неравенствами. Если при этом ν_n — малая величина, то период T_n = 2π/ν_n будет очень большим, и такое возмущение (неравенство) называется долгопериодическим.

Вначале Эйлер сделал вывод, что в упомянутом движении Юпитера и Сатурна возмущения действуют постоянно и в одном направлении. Вскоре, в 1773 г., немецкий астроном Иоганн Генрих Ламберт (1728—1777) в противовес найденному ранее обнаружил замедление Юпитера и ускорение Сатурна. Теоретические исследования Лагранжа и Лапласа привели к таким выводам: взаимное притяжение планет приводит не к вековым, но лишь к периодическим изменениям больших полуосей планет, а изменения эксцентриситетов также обладают свойствами периодичности. Именно в этом и заключался ответ на поставленный Лапласом в 1773 г. вопрос об устойчивости Солнечной системы в целом.

В 1784 г. Лапласу удалось объяснить загадочное поведение Юпитера и Сатурна: если T_J и T_S — соответственно сидерические периоды обращения Юпитера и Сатурна, то 5T_J ≈ 2T_S и в движении их из-за резонанса возникают большие долгопериодические возмущения. Изменения в долготах планет и происходят в связи с накоплением эффекта эксцентриситета. Период колебания оказался близким к 900 годам, а наибольшие отклонения по долготе у Юпитера могут доходить до 21′, у Сатурна — до 49′. Позже Лаплас об этом скажет так: «Неравенства обеих планет, которые раньше казались необъяснимыми при помощи закона всемирного тяготения, теперь составляют одно из наиболее удивительных доказательств в его пользу. Такова судьба этого блестящего открытия [Ньютона], которое любое возникающее затруднение превращает в повод для нового триумфа, — обстоятельство, являющееся вернейшим доказательством истинной системы природы».

Рис. 54. Изменение во времени эксцентриситета (а), наклона земной орбиты (б) (здесь t = 0 соответствует 1850 г.) и наклона небесного экватора к эклиптике (в)

В 1784 г. Лаплас опубликовал две теоремы об устойчивости планетной системы:

1. Если массу каждой планеты умножить на квадратный корень из большой полуоси ее орбиты и на квадрат эксцентриситета, то сумма таких произведений за вычетом периодических членов есть величина постоянная:

m₁e₁²√(a₁) + m₂e₂²√(a₂) + ... + m_ne_n²√(a_n) = const.

2. Если массу каждой планеты умножить на квадратный корень из большой полуоси ее орбиты и на квадрат тангенса наклона, то сумма этих произведений для всех планет за вычетом периодических неравенств есть величина постоянная:

m₁√(a₁) tg²i₁ + m₂√(a₂) tg²i₂+ ... + m_n√(a_n) tg²i_n = const.

Отсюда следует, что если эксцентриситет одной орбиты увеличивается, то эксцентриситет другой должен уменьшаться. Это относится и к наклонам орбит i.

После открытия Нептуна и Плутона, уточнения параметров орбиты Урана, масс Марса, Венеры и Меркурия (этих последних — по возмущениям в движении некоторых малых планет, имеющих относительно малое перигелийное расстояние) проводились повторные вычисления возмущений параметров орбит каждой из планет, пересматривался вопрос об устойчивости планетной системы в целом. Строго говоря, точного ответа на него нет и сегодня, но «вероятность устойчивости Солнечной системы очень велика»...

В частности, из расчетов следует, что эксцентриситет земной орбиты может изменяться от нуля до 0,067735, а наибольшее значение наклона земной орбиты составляет 3°6′0″ (рис. 54).