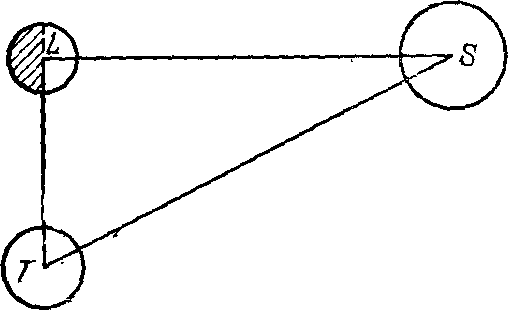
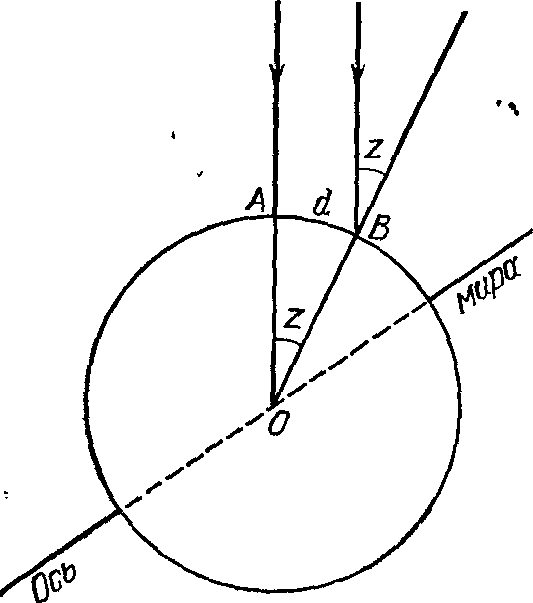
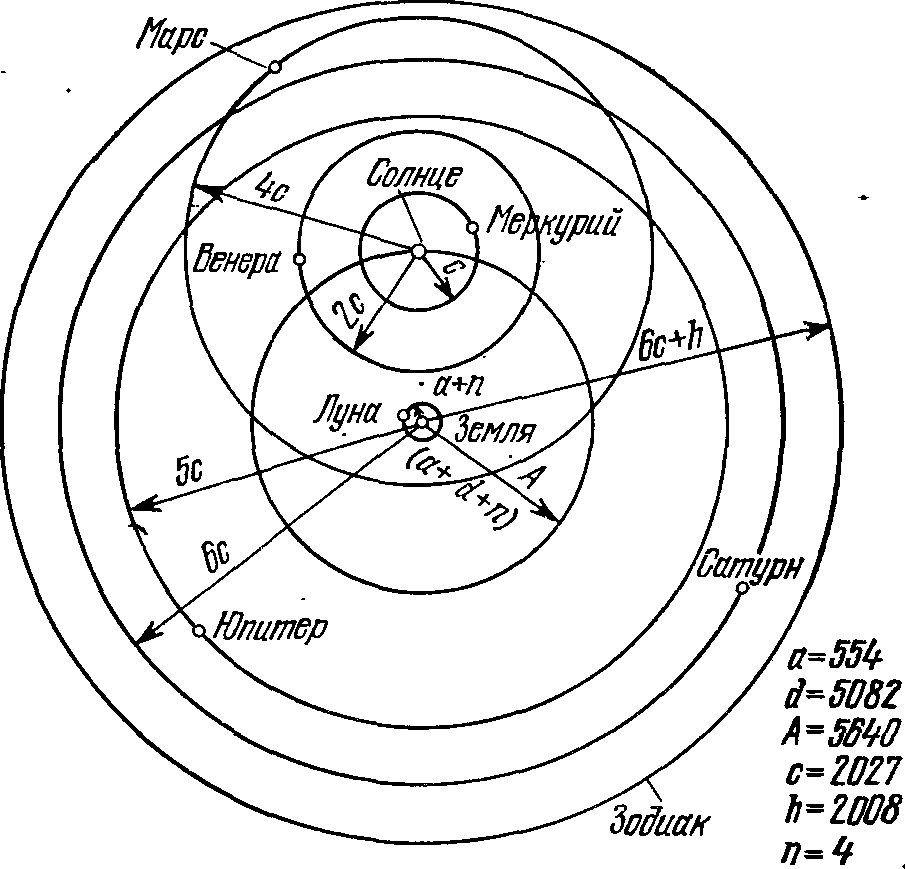
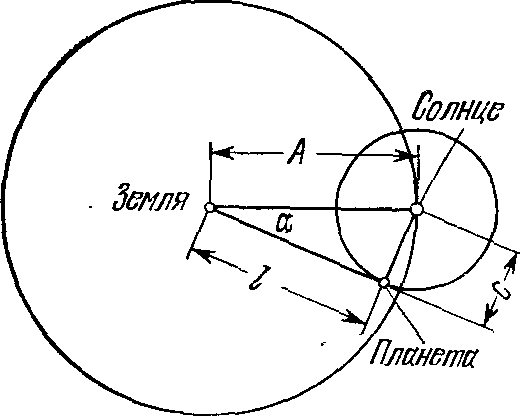
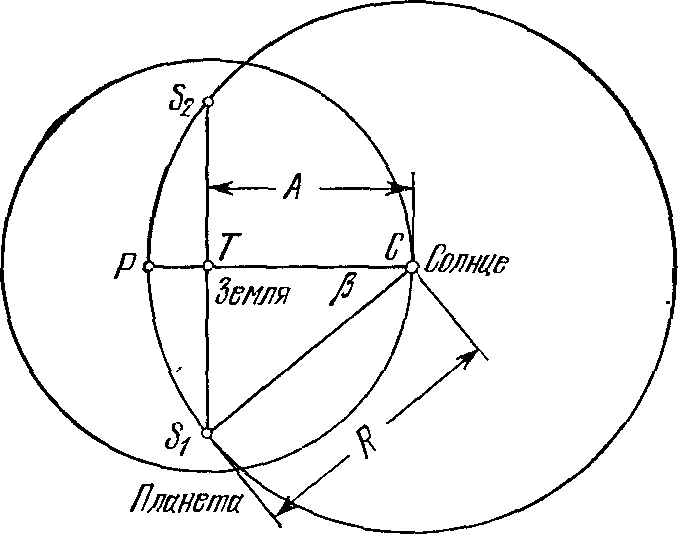
Сколько стадий до Солнца?

Коперник античного мира. Первым, кто поставил перед тобой цель измерить расстояние до небесных светил, был греческий ученый Аристарх Самосский (ок. 310 — ок. 250 гг. до н. э.). Родился он на острове Самос и некоторое время проживал в Александрии, которая была тогда столицей Египта и важным научным центром. Следует лишь напомнить, что александрийская библиотека насчитывала около 700 000 рукописных книг! Именно здесь развитие естественных наук происходило на базе строгих математических методов и наблюдений.

Есть основания полагать, что Аристарх был знаком с успехами вавилонской астрономии. Именно в это время, около 982 г. до н. э., на греческий остров Кос переселился вавилонский жрец Берос, который организовал там астрономическую обсерваторию и написал трехтомную книгу с изложением вавилонской истории и астрономии. Конечно, следует иметь в виду, что хотя древневавилонские астрономы уже умели предвидеть положение планет на небе, они совсем не интересовались ни механизмом их движения, ни вопросами о расстояниях и размерах светил.

Если же говорить о древнегреческих философах, то все количественные данные о масштабах мира, указанные в их грудах, были, конечно же, просто выдуманными и безосновательными, хотя в их высказываниях и проскальзывали весьма удачные догадки. Например, упоминавшийся выше Филолай утверждал, что расстояния небесных тел от центрального огня возрастают в геометрической прогрессии, так что каждое следующее светило расположено втрое дальше от него, чем предыдущее. Скажи он «вдвое», и за две тысячи лет предвосхитил бы правило Тициуса — Боде (с. 203)...

Несомненно, много греческих философов до Аристарха любовались Луной, наблюдали ее перемещение среди звезд. Но лишь Аристарх догадался, что после некоторых измерений и расчетов становится возможным установить расстояния в системе Солнце — Земля — Луна. Это он и сделал в труде «О величинах и расстояниях Солнца и Луны» (единственном дошедшем до нас).

Прежде всего Аристарх формулирует следующие исходные положения: «1) Луна заимствует свет от Солнца, 2) Земля по отношению к лунной сфере является точкой и центром, 3) когда Луна является нам рассеченной пополам, то большой круг, разделяющий темную и светлую части Луны, лежит в плоскости, проходящей через наш глаз, 4) когда Луна является нам рассеченной пополам, то ее расстояние от Солнца меньше четверти окружности без тридцатой части этой четверти, 5) ширина земной тени вмещает две Луны и 6) Луна стягивает пятнадцатую часть знака зодиака».

Первые три утверждения не требуют объяснений. Что же касается четвертого, то оно означает следующее: тридцатая часть четверти круга — это 3° (= 90°:30). Очевидно, что на основании собственных наблюдений Аристарх пришел к выводу, что угловое расстояние от Солнца до Луны, когда она находится в первой четверти, составляет 87° (рис. 8). В этот момент в системе Земля — Луна — Солнце угол SLT будет прямым, а угол LST равен 3° (= 90°−87°).

Рис. 8. «Треугольник Аристарха»

Аристарх продолжает: «Отсюда можно вывести, что расстояние от Земли до Солнца больше расстояния до Луны более, нежели в восемнадцать, но менее, чем в двадцать раз — на основании предположения о Луне, рассеченной пополам; что такое же отношение имеет диаметр Солнца к диаметру Луны; что диаметр Солнца к диаметру Земли имеет отношение больше чем 19 к 3, но меньше чем 43 к 6 — на основании найденного для расстояний отношения, сделанного предположения относительно тени, а также допущения, что Луна стягивает пятнадцатую часть знака зодиака».

На основании указанных выше данных сегодня школьник легко установит, во сколько же раз Луна ближе к Земле, нежели Солнце. Для этого из треугольника TLS ему необходимо найти отношения сторон TL и TS. Очевидно,

TL/TS = sin 3° = 0,0523 = 1/19,1,

Иначе говоря, если и в самом деле в первой четверти Луна размещена на угловом расстоянии 87° от Солнца, то расстояние до нее составляет 1/19 расстояния до Солнца.

Во времена Аристарха тригонометрия находилась, как это принято говорить, в зачаточном состоянии. Поэтому он получил указанный выше результат путем геометрических построений.

Аналогичным путем Аристарх приходит также к выводу, что «диаметр Солнца более чем в 18 раз и менее чем в 20 раз больше диаметра Луны», что «диаметр Луны менее двух сорок пятых, но более одной тридцатой части расстояния, на которое центр Луны удален от нашего глаза» и что «диаметр Солнца к диаметру Земли имеет отношение большее, чем 19 к 3, но меньшее, чем 43 к 6».

Можно посочувствовать ученым древности и средневековья, ведь до 1585 г. (!) они не знали, что вместо такого сравнения целых чисел (а их было нелегко подобрать) можно просто записать число с десятичной дробью...

В целом, если обозначить через R_⊕ радиус Земли, то из вычислений Аристарха следует, что

1) радиус Солнца R_☉ ≈ 7R_⊕,

2) радиус Луны R_☾ ≈ 7/19R_⊕,

3) расстояние от Земли до Луны r_☾ ≈ 19R_⊕,

4) расстояние от Земли до Солнца r_☉ ≈ 19r_☾ ≈ 361R_⊕¹.

Это был первый в истории астрономии труд, в котором расстояния между небесными телами были определены на основании наблюдений. Правда, сам результат измерений был очень неточен. Ведь угловое расстояние Луны от Солнца в момент первой четверти меньше 90° не на 3°, а всего на 9′ (причем во времена Аристарха еще не было принято делить круг на градусы). Поэтому и Солнце находится от Земли не в 19, а в 400 раз дальше, нежели Луна. Дело в том, что установить момент, когда мы видим освещенной ровно половину Луны, вообще очень трудно даже сейчас, пользуясь современными телескопами...

Но здесь более важно другое. На основании своих вычислений Аристарх нашел, что «Солнце имеет к Земле отношение большее, чем 6859 к 27, но меньшее, чем 79 507 к 216». Речь здесь идет о сравнении объемов Солнца и Земли: объем Солнца по Аристарху в 343 больше. И, по-видимому, именно эти вычисления привели его позже к выводу, что Солнце, как большее тело, размещено в центре мира и что Земля вместе с другими планетами обращается вокруг него.

Вот что писал об этой первой гелиоцентрической системе мира выдающийся ученый Архимед (ок. 287—212 гг. до н. э.) в своем труде «Псаммит» («Исчисление песчинок»): «...по представлениям некоторых астрономов, мир имеет форму шара, центр которого совпадает с центром Земли, а радиус равен длине прямой, соединяющей центры Земли и Солнца. Но Аристарх Самосский в своих «Предположениях», написанных им против астрономов, отвергая это представление, приходит к заключению, что мир гораздо больших размеров, чем только что указано. Он полагает, что неподвижные звезды и Солнце не меняют своего места в пространстве, что Земля движется по окружности вокруг Солнца, расположенного в ее центре, и что центр сферы неподвижных звезд совпадает с центром Солнца, а размер этой сферы таков, что окружность, описываемая, по его предположению, Землей, находится к расстоянию неподвижных звезд в таком же отношении, в каком центр шара находится к его поверхности...».

К сожалению, упомянутые «Предположения» Аристарха до нас не дошли. Поэтому мы практически ничего больше не знаем о тех доказательствах, с помощью которых Аристарх, этот Коперник античного мира, обосновал правильность гелиоцентрической модели мира...

Если же говорить о расстоянии от Земли до Солнца, то, как мы уже видели, Аристарх установил, будто оно в 19 раз превышает расстояние от Земли до Луны. Это число астрономы не подвергали сомнению на протяжении около 1800 лет!

И, наконец, расстояние от Земли до Луны Аристарх установил, допуская, что угловой диаметр Луны (как и Солнца) составляет 2° (именно столько составляет 1/15 часть знака зодиака, так как 12 зодиакальных созвездий вместе описывают вокруг Земли пояс протяженностью 360°). На самом же деле угловой диаметр Луны в четыре раза меньше.

Трудно сказать, почему Аристарх в этом, явно раннем, труде принял такое значение. Ведь в то время астрономы уже умели определять видимый диаметр Солнца. В частности, вавилонские жрецы делали это очень простым способом. С помощью водяных часов (клепсидры) они определяли промежуток времени, проходящий от момента касания горизонта нижнего края Солнца до момента, когда за горизонт прячется его верхний край. Очевидно, что угловой диаметр Солнца будет составлять такую часть от 360°, какую от 24 часов, в течение которых небосвод делает полный оборот, составляет измеренный отрезок времени. Вавилонские астрономы установили, что заход Солнца продолжается 2 минуты, т. е. 1/720 часть суток. Следовательно, видимый угловой диаметр Солнца составляет 360°/720= ½°.

В «Псаммите» Архимед ссылается на Аристарха, по мнению которого будто бы «видимые размеры Солнца составляют 1/720 часть его орбиты». Несомненно, Аристарх знал и истинную величину углового диаметра Луны. Однако неизвестно, осуществлял ли он на этом основании новые расчеты расстояния до Луны и Солнца...

Как видно из сказанного выше, естественной единицей при измерении расстояний до Луны и Солнца является радиус Земли. Посмотрим теперь, что было известно о его величине во времена Аристарха...

Первые землемеры. То, что Земля является шаром, убедительно обосновал Аристотель, поскольку, как он говорил, «и противоположном случае во время лунных затмений мы по видели бы на Луне такого четкого круглого сегмента... А поскольку лунное затмение образуется земной тенью, то и Земля должна иметь вид шара. Это вытекает также и из явлений, которые изображают звезды над горизонтом и из которых следует, кроме того, что земной шар не может быть очень большим. Так, достаточно лишь немного сместиться в направлении на север или на юг, чтобы круг горизонта значительно изменился, и звезды, которые раньше размещались над головой, отдалились бы от своего прежнего места...

Поэтому можно думать, что местность вокруг Геракловых столбов (Гибралтар — И.К.) соединяется с Индийской страной, и, таким образом, существует лишь одно море.

Поэтому математики, которые высчитывали окружность Земли, считают его равным приблизительно 400 тысячам стадий, а из этого мы делаем вывод, что Земля не только имеет сферическую форму, но и что ее объем незначителен по сравнению с величиной звезд».

Рис. 9. К определению радиуса Земли

Таким образом, уже Аристотелю была известна длина большой окружности, опоясывающей нашу планету, S = 400 000 стадий. А так как S = 2πR_⊕, то отсюда определить можно и радиус Земли R_⊕. Приняв для стадии ее наименьшее значение 157,5 м, находим S = 63 000 км и R_⊕ = 10 032 км. Как видно, даже в этом случае радиус Земли оказывается преувеличенным почти в 1,6 раза. Но это, по сравнению с более ранними догадками, все же неплохой результат!

Имен математиков, впервые установивших (хотя и приближенно) величину радиуса Земли, мы не знаем. Возможно, среди них был Пифагор или его ученики, поскольку эта проблема является, по существу, несложной геометрической задачей. В самом деле, пусть наблюдатель находился вначале в пункте A и обнаружил, что определенная звезда проходит здесь через зенит. Пусть далее наблюдатель перемещается строго на север (вдоль меридиана). Пройдя расстояние d, он заметит, что то же светило уже проходит через меридиан на угловом расстоянии z от зенита (рис. 9). Напрашивается вывод, что если бы наблюдатель совершил путешествие вокруг земного шара, пройдя путь S = 2πR_⊕, т. е. описал относительно центра Земли дугу в 360° и возвратился снова в точку A, то картина прохождения избранной звезды через зенит восстановилась бы. На этом основании нетрудно составить такую пропорцию: длина земной окружности S будет во столько раз больше длины дуги d, во сколько раз полный угол 360° больше угла z. Таким образом,

S = (360°/z)d.

В том факте, что Аристотель приводит число, по которому радиус Земли в полтора раза превышает его истинное значение, нет ничего удивительного. Ведь для точного измерения угловых расстояний звезд от зенита в то время еще не было надежных инструментов. К тому же само расстояние d между пунктами A и B могло быть определено неточно. Ведь для того, чтобы зенитное расстояние увеличилось всего на Г, наблюдатель должен сместиться вдоль меридиана на 111 км.

Получить более точные размеры нашей планеты удалось древнегреческому математику и астроному Эратосфену (ок. 276 — ок. 194 гг. до н. э.). Эратосфен обнаружил, что в полдень самого длинного дня лета, когда Солнце в небе находится в наивысшем положении и его лучи в г. Сиене (теперь Асуан) падают вертикально, освещая дно глубоких колодцев, в Александрии в это же время зенитное расстояние Солнца составляет 1/50 полного круга (т. е. 7°12′). Расстояние между Сиеной и Александрией оценивалось в 5000 египетских стадий. На основании приведенных выше рассуждений Эратосфен установил, что длина окружности меридиана составляет 250 000 стадий. Если стадия соответствовала 157,5 м, то это составляло 39 500 км, а радиус Земли должен был равняться 6290 км. Таким образом, погрешность измерения в данном случае составляла бы всего 1,3%.

Для измерения зенитного расстояния Солнца Эратосфен установил на городской площади в Александрии угломерный прибор (солнечные часы) скафис, принцип работы которого был очень прост. В центре чаши, имеющей форму полусферы, вертикально устанавливали заостренный стержень. На внутренней поверхности чаши, куда от него падала тень, были нанесены горизонтальные окружности, соответствующие определенным высотам Солнца над горизонтом. Отклонения же тени от направления «север — юг» давали возможность измерять время.

По-видимому, с помощью того же скафиса Эратосфен установил также, что угол наклона плоскости эклиптики к плоскости экватора составляет ε = 23°51′. Этот вывод был сделан на том основании, что разность между высотами Солнца в меридиане во время летнего и зимнего солнцестояний составляет 11/83 полной окружности, т. е. 47°42′. А это и является удвоенным значением угла ε.

Система мира Архимеда. Архимед, которого римский историк Тит Ливий (59 г. до н. э. — 17 г. н. э.) назвал «единственным в своем роде созерцателем неба и звезд», родился в Сиракузах на острове Сицилия, а учился в Александрии, где познакомился с астрономами Кононом и Эратосфеном. Эти сведения можно найти в уже упоминавшемся «Псаммите». Архимед провел подсчет числа песчинок во Вселенной в получил результат 10⁶³. Архимед создал систему мира с указанием конкретных расстояний до планет. Сведения об этой системе мира Архимеда (точнее, о расстояниях до орбит планет, из которых следуют определенные выводы о ней) содержатся в сочинении римского епископа Ипполита (первая половина III в. н. э.), а в меньшей степени — в комментариях римского писателя V в. Макробия. Ипполит и «Опровержении всех ересей» пишет следующее:

«Расстояние от поверхности Земли до лунной орбиты сам... Аристарх оценивает в своем сочинении в... стадий, Архимед же в 554 мириады 4130 единиц стадий; от лунной до солнечной орбиты стадий 5026 мириад 2065 единиц, от нее до орбиты Венеры стадий 2027 мириад 2065 единиц, от нее до орбиты Меркурия стадий 5081 мириада 7165 единиц, от пес до орбиты Марса стадий 4054 мириад 1108 единиц, от нее до орбиты Юпитера стадий 2027 мириад 5065 единиц, от нее до орбиты Сатурна стадий 4037 мириад 2065 единиц, от нее же до зодиака и самой последней окружности стадий 2008 мириад 4005 единиц. Таковы переданные Архимедом расстояния орбит друг от друга и глубины сфер; периметр же зодиака он принимал стадий 4 вторых числа 4731 мириада, таким образом, получается, что расстояние от центра Земли до самой крайней поверхности будет шестой частью упомянутого числа, расстояние же от поверхности Земли, на которой мы живем, до зодиака получится, если шестую часть упомянутого числа уменьшить на 4 мириады стадий, которые представляют расстояние от центра Земли до ее поверхности. От орбиты Сатурна до Земли, как он говорит, будет вторых чисел одна единица 2160 мириад 8259 единиц, от Меркурия до Земли 5268 мириад 8259 единиц, от Венеры до Земли 5081 мириада 5160 единиц... так вот расстояния и глубины сфер Архимед дает такими».

Здесь мириада — 10 000, «вторыми числами» Архимед называл десятки тысяч мириад.

Здесь же Ипполит говорит о том, что изложенные Архимедом числа не находятся в созвучных отношениях, «то есть в так называемых платоновских двойных и тройных», а поэтому, дескать, «они не могут сохранить гармоничного строения вселенной».

Макробий о том же пишет более скупо: «Также и Архимед считал, что он определил число стадий, на которое от поверхности Земли удалена Луна, а от Луны — Меркурий, от Меркурия — Венера, от Венеры — Солнце, ...все же расстояние от Сатурна до самого звездоносного неба он, как думал, измерил только рассуждением. Однако это архимедово измерение отвергнуто платониками как не сохраняющее двойных и тройных интервалов».

Рис. 10. Реконструкция гео-гелиоцентрической системы мира Архимеда

На основе противопоставления действий — «определил» и «измерил рассуждением» — можно думать, что расстояния до планет Архимед вычислил из наблюдений. Кстати, указанная в тексте Ипполита операция получения «шестой части числа» означает деление длины окружности на 2π, чтобы получить радиус сферы звезд (более точного значения числа π, чем π = 3, тогда еще не знали).

Беда всех древних текстов в том, что они со временем сами по себе подвергаются порче (а ведь от Архимеда до Ипполита прошло более 400 лет!). К тому же зачастую выборку чисел из них делают люди, мало сведущие в изложенном материале. Ошибаются и переписчики...

Исходя из простейших логических соображений, недавно С.В. Житомирский выполнил реконструкцию числовых данных Архимеда². И — взору читателя предстает стройная гео-гелиоцентрическая модель мира, в которой Меркурий, Венера и Марс обращаются вокруг Солнца, которое вместе с ними, а также Юпитер и Сатурн, движется вокруг Земли (рис. 10). При этом относительные радиусы орбит Меркурия, Венеры и Марса довольно хорошо совпадают с их истинными значениями!

Необходимость реконструкции видна из следующего. Сначала Ипполит указывает числа «до орбиты», скажем, Венеры, немногим же ниже даются отдельно расстояния «от Меркурия до Земли» и «от Венеры до Земли», причем, как нетрудно убедиться, они не совпадают с предыдущими.

Рис. 11. К определению Архимедом расстояния до Меркурия

А ведь в геоцентрической системе расстояние до Меркурия (также до Венеры и Марса) просто равно радиусу орбиты планеты...

Реконструированные расстояния выглядят так: от поверхности Земли до Луны a = 554 мр (для сокращения буквами «мр» обозначены мириады стадий, числа единиц стадий округлены), от лунной до солнечной орбиты d = 5082 мр, поэтому расстояние от центра Земли до Солнца A = a + d + n = 5640 мр (n = 4 мр — радиус Земли), дальше от Солнца до орбиты Меркурия c = 2027 мр, от нее до орбиты Венеры также c, от орбиты Венеры до орбиты Марса 2c, дальше радиус орбиты Юпитера (предположительно) 5c и Сатурна 6c 12 162 мр — число, указанное Ипполитом. От орбиты Сатурна до зодиака h = 2008 мр и для согласования с укачанным у Ипполита числом «периметра зодиака» следует читать «полупериметр». В этом одно из возможных доказательств правильности реконструкции.

Далее легко убедиться, что предположительное расстояние от центра Земли до Солнца (Л), расстояние «от Меркурия до Земли» (число l = 5269 мр) и число c — расстояние от Солнца до Меркурия с высокой точностью подчиняются теореме Пифагора: √(5640² − 2027²) = 5264! Но отношение l/A = 5268/5640 = 0,934 — это косинус угла а, соответствующего средней наибольшей элонгации Меркурия: arccos 0,934 = 21°02′ (рис. 11). Становится понятным, почему это число вообще фигурирует в тексте: оно указывает среднее значение элонгации планеты.

Аналогичным образом, по-видимому, был определен и радиус орбиты Венеры. В случае же Марса, обращающегося вокруг Солнца, задача решается также сравнительно легко (рис. 12). Для этого необходимо зафиксировать число дней N, истекших от противостояния Марса до квадратуры. Зная синодический период обращения планеты S = 780 сут и полагая, что планета движется по круговой орбите равномерно, находим угол β = (360°/S)N, после чего имеем R = A/cos β.

Рис. 12. Решение задачи о расстоянии до Марса в системе мира Архимеда

Примечательно, что относительные расстояния от Солнца до Меркурия, Венеры и Марса — c/A, 2c/A, 4c/A, равные соответственно 0,36, 0,72 и 1,44, довольно близки к их истинным значениям (0,39, 0,72 и 1,52). В абсолютных же еди-ницах при длине стадии 177,5 м в мире Архимеда имеем: расстояние от центра Земли до Луны равно 990450 км — почти в 2,6 раза больше, а от Земли до Солнца — 10 011 000 км, в 15 раз меньше истинного. Радиус сферы звезд всего в 2,5 раза больше расстояния от Земли до Солнца.

В «Псаммите» Архимед сообщает, что он измерил видимый угловой диаметр Солнца, который лежит в пределах между 1/164 и 1/200 частями прямого угла. Приняв среднее значение 1/180 прямого угла или 30′, нетрудно найти, при известных уже расстояниях до Солнца и Луны (угловой диаметр которой такой же), их линейные размеры: диаметр Солнца 49,2 мр, Луны 4,8 мр, т. е. Луна будто бы в 10,2 раза меньше Солнца.

Из всего сказанного здесь видно, что Архимед был не просто «созерцателем неба и звезд», а искусным наблюдателем и глубоким мыслителем. И приходится сожалеть, что его астрономические труды практически не дошли до нас...

О «небесном глобусе» Архимеда. На протяжении нескольких столетий после смерти Архимед оставался известным и как создатель удивительного «самодвижущегося прибора» — механического «небесного глобуса», с помощью которого демонстрировались условия видимости светил, затмения Солнца и Луны. Вот как писал об этом Цицерон в трактате «О государстве»: «...сплошная сфера без пустот была изобретена давно и такую сферу впервые выточил Фалес Милетский, а затем Евдокс Книдский, по словам, ученик Платона, начертал на ней положение созвездий и звезд, расположенных на небе..., спустя много лет Арат, руководясь не знанием астрономии, а, так сказать, поэтическим дарованием, воспел в стихах все устройство сферы и положение светил на ней, взятое им у Евдокса. Но... такая сфера, на которой были бы представлены движения солнца, лупы и пяти звезд, называемых странствующими и блуждающими, не могла быть создана в виде сплошного тела; изобретение Архимеда изумительно именно тем, что он придумал, каким образом при несходных движениях, во время одного оборота сохранить неодинаковые и различные пути. Когда Галл приводил эту сферу в движение, происходило так, что на этом шаре из бронзы луна сменяла солнце в течение стольких же оборотов, во сколько дней она сменяла его на самом небе, вследствие чего и на небе сферы происходило такое же затмение солнца, и луна вступала в ту же межу, где была тень земли, когда солнце из области...»³.

И дальше, увы, часть текста трактата утеряна... Как отмечалось выше, в системе мира Архимеда планеты (по крайней мере, Меркурий, Венера и Марс) обращались вокруг Солнца. Поэтому моделирование петлеобразных видимых движений нижних планет (Меркурия и Венеры) выполняется «само собой». О том же, как Архимеду удавалось изображать (если это вообще достигалось) петлеобразные движения верхних планет (Марса, Юпитера и Сатурна), приходится лишь гадать...

О модели Архимеда Цицерон еще раз упоминает в трактате «О природе богов» и в «Тускуланских беседах». Из текста следует, что после Архимеда такой же небесный глобус сконструировал и Посидоний: «Если бы кто-нибудь привез в Скифию или Британию тот шар (Sphaera), что недавно изготовил наш друг Посидоний, шар, отдельные обороты которого воспроизводят то, что происходит на небе с Солнцем, Луной и пятью планетами в разные дни и ночи, то кто в этих варварских странах усомнился бы, что этот шар — произведение совершенного рассудка?»⁴.

Вглядываясь в это чудо техники, зритель неминуемо ставил себе и дальнейшие вопросы, как это видно из «Первой книги против физиков» представителя античного скептицизма Секста Эмпирика (II—III вв. н. э.): «Самодвижущиеся приборы удивительнее тех, которые не таковы. Когда мы смотрим на Архимедову сферу, мы сильно изумляемся, видя, как движутся Солнце, Луна и прочие звезды. Конечно, нас поражает не материал и не движение частей механизма, но его творец и движущие причины. ...Согласно же высшей точке зрения, удивительнее всего... оказывается природа Солнца, Луны и звезд, и, прежде всего, самого мира, которая и есть причина всего этого»...⁵

Примечания

1. Веселовский И.Н. Аристарх Самосский — Коперник античного миря // ИАИ. — 1961. — Вып. VII. — С. 44.

2. Житомирский С.В. Астрономические работы Архимеда // ИАИ. — 1977. — Вып. XIII — С. 319—337; Античные представления о размерах мира // ИАИ. — 1983. — Вып. XVI. — С. 291—326.

3. Цицерон. Диалоги. — М.: Наука, 1966. — С. 14.

4. Цицерон. Философские трактаты. — М.: Наука, 1985. — С. 129.

5. Секст Эмпирик. Сочинения: Т. 1. — М.: Мысль, 1976. — С. 264.