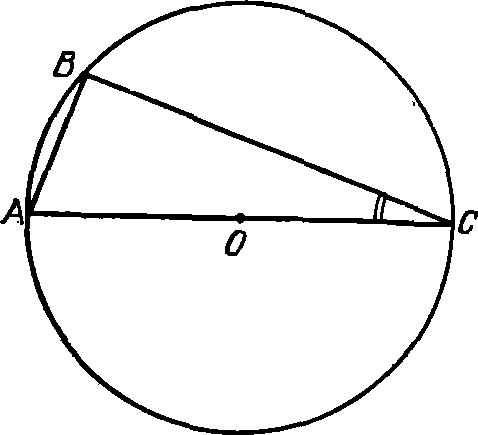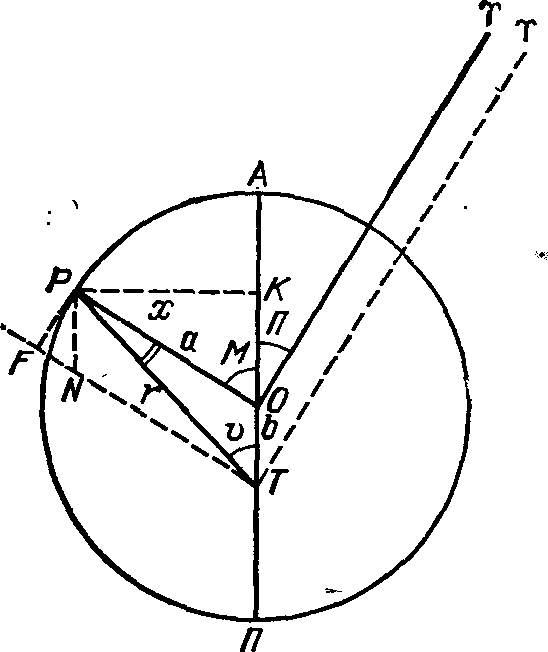
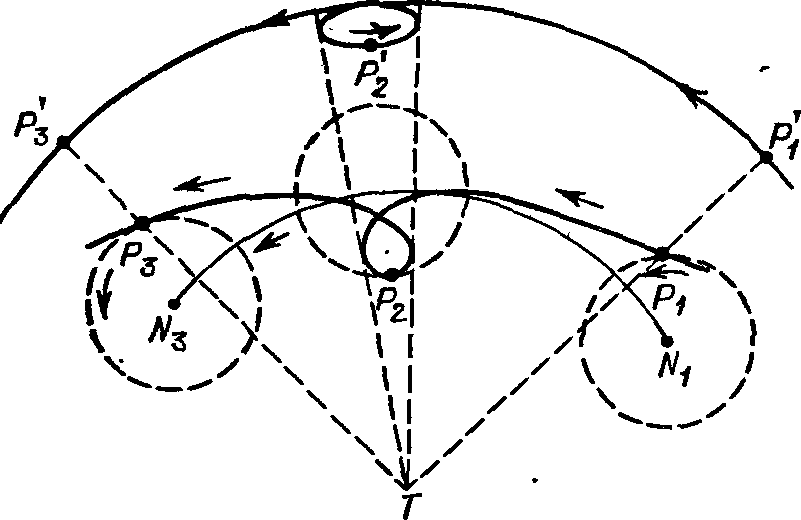
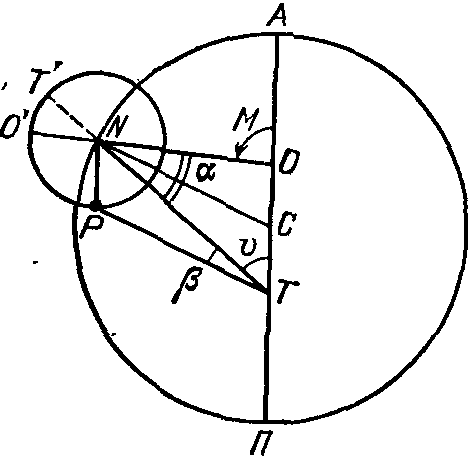
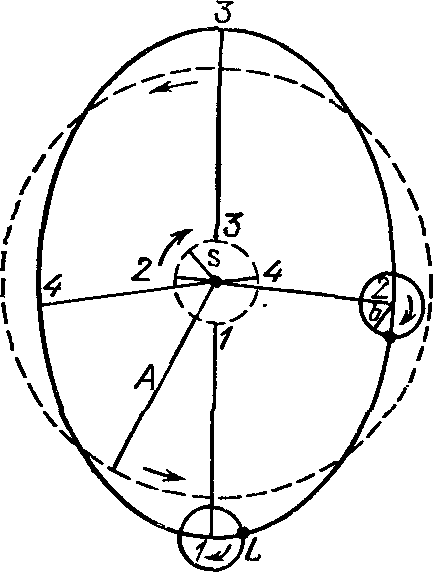
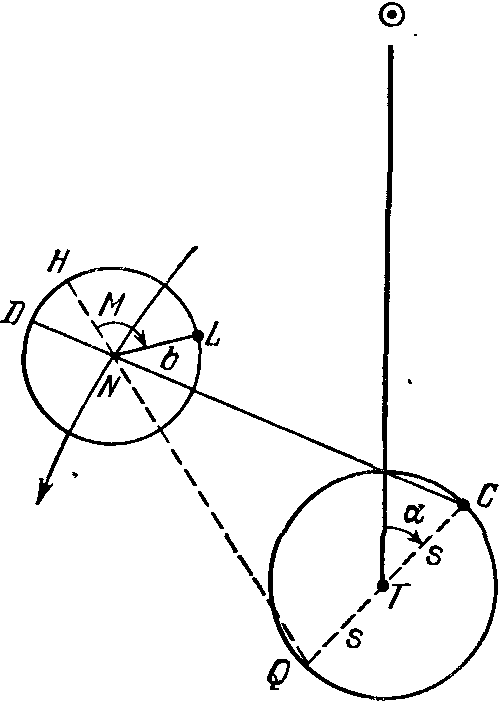
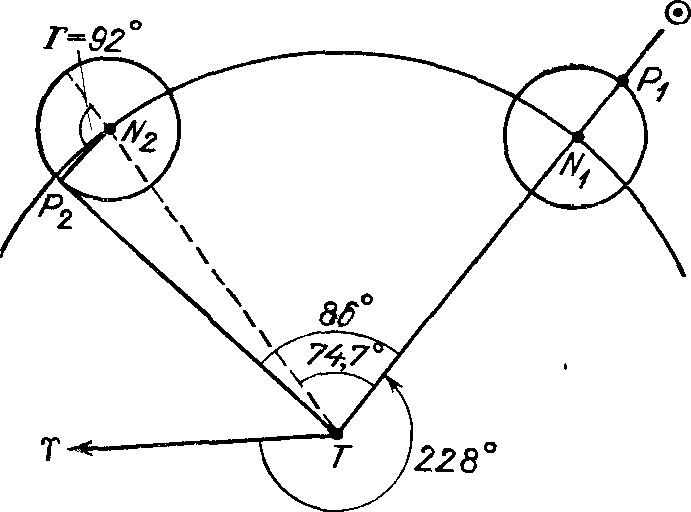
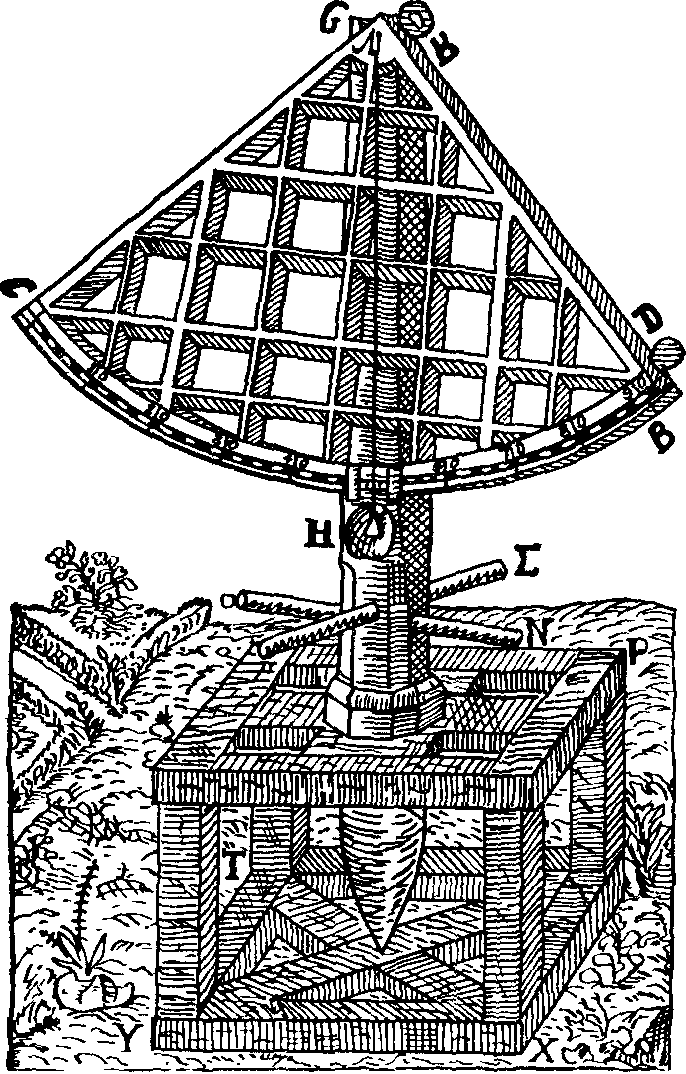
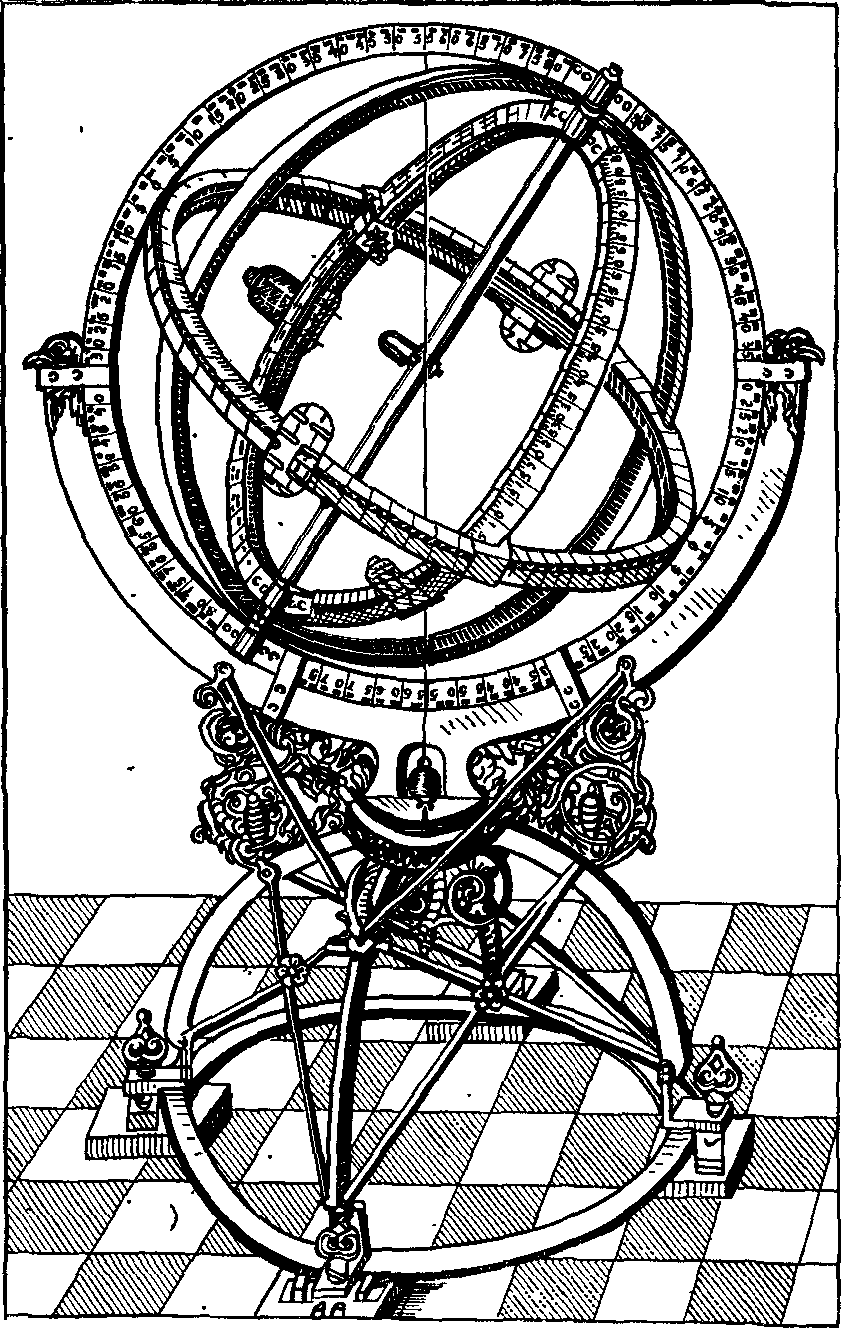
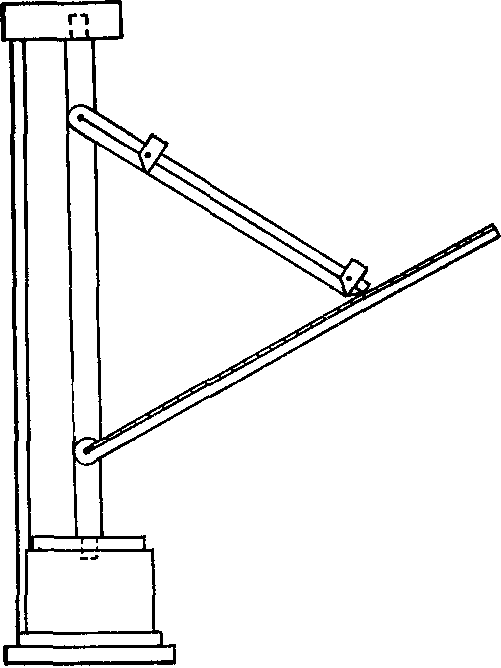
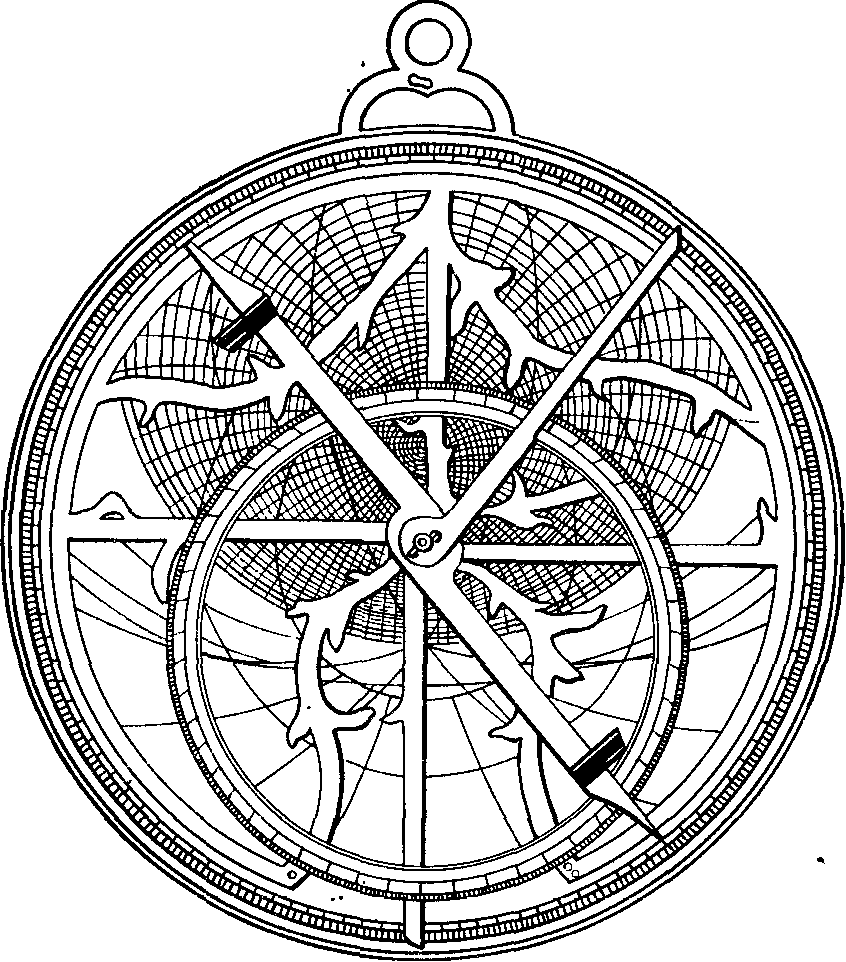
«Математический синтаксис» Птолемея

О первых четырех книгах. «Что я смертен, я знаю, и что дни мои сочтены; но когда я в мыслях неустанно и жадно выслеживаю орбиты созвездий, тогда я больше не касаюсь ногами Земли: за столом Зевса наслаждаюсь амброзией, пищей богов».

Так звучит эпиграф к книге Клавдия Птолемея, которую он сам назвал «Математикес синтаксеос библиа 13» — «Математический трактат по астрономии в 13 книгах». Но уже вскоре эту книгу начали называть «Мегале синтаксеос» («Великое построение») и «Мэгисте» («Величайшее»). Добавив к последнему названию артикль «аль», арабские астрономы «передали» европейцам (это произошло лишь в конце XII в.!) ее современное название «Альмагест».

Впервые типографским способом «Альмагест» был опубликован на латинском языке в Венеции (1515 г.) как перевод с арабского текста, а в 1528 г. там же осуществлено издание перевода с греческих рукописей. На греческом языке «Альмагест» был напечатан в г. Базеле (1538 г.) и Копенгагене (1898 и 1903 гг.) и на немецком языке — в г. Лейпциге (1912 г. и 1963 г.). Перевод «Альмагеста» на русский язык осуществлен И.Н. Веселовским и, будем надеяться, он вскоре будет опубликован.

Об авторе «Альмагеста» — книги, которая была своеобразной энциклопедией античной астрономии, — мы знаем очень мало. Известно лишь, что он родился в Египте, что и 127—141 гг. н. э. проводил наблюдения в Александрии, а умер около 168 г. н. э.

Следует сказать, что в середине II в. до н. э. Греция попала в зависимость от Рима, а в 30-х годах I в. до н. э. та же участь постигла и Египет. Но Александрия некоторое время еще оставалась крупным научным центром.

«Альмагест» состоит из 13 книг, а его объем в немецком падании 1912 г. составляет 908 страниц. В первой книге изложены основные принципы, на которых основываются все дальнейшие выкладки и построения. Исходные утверждении состоят в том, что «небосвод имеет шарообразную форму и вращается, как шар», «Земля является шаром и расположена в центре мира», «Земля является точкой по сравнению с расстоянием до неподвижных звезд» и что «не имея никакого движения, земля не меняет места своего расположения».

Свои утверждения Птолемей обосновывает, исходя из основных положений аристотелевой философии. Не называя имени Аристарха, Птолемей спорит с теми, «кто считает небесную сферу покоящейся, тогда как Землю заставляет вращаться вокруг своей оси с запада на восток, совершая одно обращение в сутки». Это вращательное движение Земли, дескать, было бы очень стремительным, а его скорость чрезмерной, так как за 24 часа необходимо было бы описать всю окружность Земли. Из-за этого будто бы тела не могли бы беспрепятственно падать на Землю, да и все, что не прикреплено к ней прочно, должно было бы отставать от движения Земли, двигаться в противоположную сторону — на запад. А этого, мол, мы не наблюдаем.

Сегодня мы знаем, что Птолемей в данном случае сильно переоценивал роль центробежной силы, возникающей при вращении любого тела. Однако следует сказать, что в подтверждение своей геоцентрической системы мира он приводил именно физические, а не какие-нибудь общефилософские рассуждения.

Рис. 18. Зарождение тригонометрии: величина угла С определяется длиной хорды AB

Значительная — часть первой и второй книг посвящена элементам сферической астрономии. Здесь, в частности, Птолемей привел теоремы о плоских и сферических треугольниках, впервые описал метод измерения дуг (углов) по величинам стягивающих их хорд (прообраз современных синусов) и составил соответствующую таблицу. Расчет хорд Птолемей осуществлял следующим образом: в окружность вписывал прямоугольный треугольник, гипотенузой которого был диаметр (рис. 18). Очевидно, что при передвижении вершины прямого угла вдоль дуги окружности этот угол всегда остается прямым, величина же одного из двух других растет от 0° до 90° (Птолемей считал, что прямой угол содержит 180°, и следовательно, величина остальных углов изменялась от 0° до 180°), а длина стороны, противоположной этому острому углу (т. е. хорды, стягивающей соответствующую ему дугу), — от нуля до величины диаметра окружности. Поскольку греки в то время не знали десятичных дробей, а применяли шестидесятеричную систему, было удобно измерять Длину диаметра каким-нибудь большим числом. Птолемей принял его равным 120. Тогда, в частности, для дуги 90° длина хорды записывалась так: 84^p51′10″, т. е. 84+51/60+10/3600¹. Чтобы перейти к современным обозначениям, разделим указанный угол на 2, а длину хорды на 120^p, в результате чего получим sin 45°= 0,7071.

Здесь же Птолемей обсуждает методы расчета угла наклона эклиптики к горизонту, моментов и продолжительности восхода некоторых зодиакальных созвездий в зависимости от географической широты наблюдателя, понятие о которой, кстати, также ввел он сам. Отдельные главы содержат информацию «О том, как вычисляется, где, когда и сколько раз Солнце бывает прямо над головой» и «О том, как на основании изложенного определяются отношения гномонов к полуденным теням во времена равноденствий и солнцеворотов».

В третьей книге Птолемей излагает теорию видимого годичного движения Солнца, «без которой, в свою очередь, невозможно полностью охватить всё, касающееся Луны». В первой главе «О продолжительности года» Птолемей сравнивает даты равноденствия, наблюдавшиеся им самим, с соответствующими наблюдениями Гиппарха, осуществленными на 285 лет раньше. Это и дало ему возможность установить, что «за 300 лет возвращение Солнца к точке весеннего равноденствия происходит на день раньше, чем должно быть, если год равен 365¼ дня». Отсюда следовало, что продолжительность тропического года составляет 365 дней 5 часов 55 минут 12 секунд — на 6 минут больше истинного².

В четвертой книге рассматривается продолжительность синодического месяца, излагается теория движения Луны. В пятой идет речь об устройстве астролябии, об особенностях движения Луны, далее — «Определение расстояния Луны», «О величинах видимых диаметров Солнца, Луны и земной тени в сизигиях»³, «О расстоянии Солнца и о том, что определяется вместе с ним», «О величинах Солнца, Луны и Земли» и о значениях и определениях параллаксов Солнца и Луны. В шестой книге изложена теория солнечных и лунных затмений. В седьмой и восьмой книгах дан каталог 1022 звезд. Здесь же Птолемей приводит свои результаты определения значения прецессии, причем указывает число, точно совпадающее с гиппарховым: точка весеннего равноденствия перемещается навстречу Солнцу на 1° за сто лет; здесь же он дает описание Млечного Пути и посвящает целую главу устройству небесного глобуса.

В остальных пяти книгах изложена теория планетных движений.

Кроме указанных неточностей в определении продолжительности тропического года и прецессии, обращает на себя внимание и тот факт, что координаты звезд в каталоге Птолемея очень точно совпадают с соответствующими их значениями по каталогу Гиппарха, если учесть заниженное (!) значение годичной прецессии (36″). Это дало повод многим астрономам XVIII—XIX вв. утверждать, что сам Птолемей вообще наблюдений не проводил, а лишь пересчитал данные Гиппарха на свое время или же осуществлял эти наблюдения очень грубо⁴.

Конечно, вполне можно допустить, что, имея полученные Гиппархом данные о продолжительности года (как и о значении прецессии), Птолемей (или его помощник) рассчитал даты солнцестояний и равноденствий (соответственно — координаты звезд) и выдал их за наблюденные (иначе говоря, произвел наблюдения крайне грубо, ориентируясь на эти расчеты). Но ведь главное, чем прославился Птолемей, — это его модель движения планет, позволявшая, как-никак, делать предвычисления положений планет на десятки лет вперед! И здесь, раньше чем утверждать, что Птолемей «сфабриковал все наблюдения», следовало бы доказать, что у него для каждой из планет уже были необходимые параметры задачи: отношения размеров радиуса эпицикла и деферента, угловых скоростей движения планеты по эпициклу и центра эпицикла по деференту и т. д. Без них ведь фабрикация положений планет в принципе невозможна! Остается непонятным удивление Р. Ньютона тем, что «наблюдавшаяся долгота совпадает с вычисленной лучше 1′». Но иначе ведь и быть не может, если только теория построена на основе этих наблюдений.

Несомненно, что книга Р. Ньютона сыграет большую положительную роль в изучении античной астрономии (для этого необходимо скорейшее издание «Альмагеста» на русском языке), и начать здесь, видимо, следует с вопроса о том, под силу ли было вообще одному человеку в середине II в. н. э. самому и без ошибок (этих нежелательных спутников почти каждого научного исследования) выполнить весь изложенный в «Альмагесте» объем работы. Ведь не исключено, что мы, умудренные 2000-летним опытом развития астрономии, имея в своем распоряжении мощные телескопы с высокоточными координатно-измерительными машинами и производящие миллион операций в секунду ЭВМ, напрасно укоряем в ошибках (тем более — обвиняем в сознательных подделках) человека, измерявшего углы с помощью трех линеек и проводившего расчеты, пользуясь, образно говоря, всего лишь горстью камешков...

Нельзя, скажем, не отметить тот факт, что в движении Луны Птолемей открыл (а это требовало продолжительных наблюдений и притом довольно точных!) так называемое неравенство эвекции. Он установил, что положение Луны на небесной сфере отклоняется от рассчитанного после учета (!) «первого неравенства»: в первой четверти Луна уходит вперед на 76′ в третьей она на столько же отстает.

Вне всякого сомнения Птолемея можно назвать одним из самых выдающихся математиков древнего мира. Ведь лишь гиганту была под силу столь огромная и кропотливая работа — синтез всех достижений астрономии и построение на этой основе стройной геометрической модели мира. И, как отметил А. Паннекук, «Математическое сочинение» было карнавальным шествием геометрии, праздником глубочайшего создания человеческого ума в представлении вселенной... Труд Птолемея предстает перед нами как величественный памятник науки античной древности»⁵.

Элементы теории. В третьей книге «Альмагеста» Птолемей рассматривает задачу о движении Солнца по эклиптике. Вслед за Гиппархом он рассматривает возможность представления этого движения эксцентром или комбинацией эпицикла и деферента и останавливается на первом, учитывая, что гипотеза эксцентра проще, так как она достигает цели с помощью лишь одного движения. Здесь же даны таблицы для определения положения Солнца на эклиптике. Сущность расчета заключается в следующем. Пусть O (рис. 19) — центр эксцентра, T — положение Земли, P — Солнце, A — апогей его орбиты, Oγ и Tγ — направление на точку весеннего равноденствия, от которого отсчитывается долгота апогея Π, средняя долгота Солнца λ̅ и его истинная долгота λ. Очевидно, что λ = Π + M − x, где M — по Птолемею — аномалия, x = М − v — уравнение центра, или простаферезис. Здесь M = 360°/T(t − t₀), где t₀ — время прохождения Солнца через апогей, T — тропический год. Из треугольников PKO, PKT, PFT и PFN нетрудно получить в. аналитическом виде зависимости x, v и расстояния до Солнца r от M и значения эксцентриситета ε = OT/OP. Мы ограничимся здесь замечанием, что при найденном Гиппархом значении эксцентриситета ε = 1/24 = 0,0417 наибольшее значение уравнения центра достигается при M = 90°, и оно равно 2°23′: на столько Солнце, двигаясь от апогея к перигею, отстает в своем движении от «среднего Солнца» и, наоборот, обгоняет его при движении от перигея к апогею.

Рис. 19. К определению «первого неравенства», численное значение которого было основным элементом солнечных таблиц на протяжении почти 2000 лет

Решение задачи о движении Луны, полученное Птолемеем, рассмотрено ниже. Здесь же остановимся на кинематике эпициклов, столь удачно использованной им для построения геоцентрической модели мира. Но сначала напомним, что, как и Солнце, планеты движутся примерно вдоль эклиптики неравномерно, и в этом проявляется «первое неравенство» их движения. Неравномерность же в движении планет по сравнению с Солнцем была названа «вторым неравенством». Так, для одной группы планет (Марс, Юпитер, Сатурн) характерно то, что в процессе своего движения вдоль эклиптики они отстают от Солнца, т. е. Солнце их догоняет и обгоняет, несмотря на то, что они, как и Солнце, перемещаются среди звезд с запада на восток. Напомним также, что момент, когда Солнце и планета оказываются на одной линии с наблюдателем, причем расположены по одну сторону от него, называется соединением планеты с Солнцем, а момент, когда Солнце и планета расположены по разные стороны от наблюдателя, — противостоянием. Именно находясь в противоположной к Солнцу части неба, планета останавливается, движется в обратном, к западу, направлении, снова останавливается, после чего продолжает свое движение среди звезд с запада на восток. В момент противостояния планета находится в середине дуги попятного движения (см. рис. 2).

Планеты второй группы (Меркурий и Венера) ведут себя совсем иначе: они то обгоняют Солнце, двигаясь на восток, и тогда они видны вечером, то останавливаются и начинают обратное движение, исчезают в лучах Солнца (нижнее соединение планеты с Солнцем), после чего появляются на небе утром. Угловое расстояние планеты от Солнца увеличивается до наибольшего значения (эта наибольшая элонгация для Меркурия составляет 18—28°, для Венеры 43—48°), после чего происходит сближение планеты с Солнцем и ее верхнее соединение с ним, а затем появление планеты на вечернем небе.

Как уже отмечалось, промежуток времени, на протяжении которого планета по отношению к Солнцу занимает то же положение на небе, называется синодическим периодом движения планеты.

Задачей теории и было разработать метод, с помощью которого можно было бы вычислять долготы планет с учетом «первого» и «второго» неравенств. Решить ее Птолемею удалось с помощью комбинаций деферентов и эпициклов, причем для планет необходимо было вводить два отдельных параметра: угловую скорость движения центра эпицикла по деференту со и угловую скорость движения планеты в эпицикле σ. Третьим параметром задачи было отношение радиуса эпицикла b к радиусу деферента а, δ = b/a.

Рис. 20. К объяснению петлеобразного движения планет в системе мира Птолемея

Используя систему эпицикл — деферент, нетрудно получить в проекции на небесную сферу петлеобразное движение планеты. Пусть в определенный момент времени планета находится на эпицикле в точке P₁ (рис. 20), а центр эпицикла — на деференте в точке N₁. В процессе равномерного кругового движения обеих точек — планеты с угловой скоростью σ вокруг точки N и самой точки N (ее принято называть «средней планетой») как центра эпицикла с угловой скоростью со вокруг Земли — планета опишет петлю, которую наблюдатель видит в проекции на небесную сферу.

Причина образования петли очевидна: в точке P₁ движения по эпициклу и по деференту направлены в одну сторону — справа налево. Описав дугу в 180°, планета движется по эпициклу слева направо. Поскольку же угловая скорость σ больше, чем ω, направление видимого движения в положении, близком к P₂, изменяется — планета здесь движется с востока на запад.

Рис. 21. К определению долготы планеты λ

Так при помощи эпициклов Птолемею удалось учесть «второе неравенство» в движении планет. Что же касается «первого неравенства», то для его учета он разработал теорию «биссекции эксцентриситета», т. е. его равного деления.

Эту теорию известный советский историк астрономии Н.И. Идельсон (1885—1951) назвал шедевром античной науки. Сущность ее заключается в следующем⁶.

Рис. 22. Движение Луны по Птолемею

Пусть (рис. 21), как и раньше, T — центр эклиптики, в котором находится наблюдатель, O — центр равномерного движения, причем OT = εa. Птолемей разделил отрезок OT пополам и далее рассматривал движение «средней планеты» (т. е. центра эпицикла) по окружности с центром в точке C. Но принималось, что движение «средней планеты» будет равномерным не относительно точки C, а относительно точки O, т. е. постоянная угловая скорость вводилась лишь для направления ON. Позже европейские астрономы (при составлении «Альфонсинских таблиц», см. раздел «Канун революции») назвали точку О эквантам (так же была названа и окружность с центром в точке O).

Вычисление долготы планеты λ проводилось в таком порядке: предварительно задавался момент t₀ перехода центра эпицикла через точку A (апогей), в это время истинная планета P также находилась на линии ТА (!). Далее для каждого последующего момента t рассчитывался угол равномерного отклонения M от апогея: M = ω(t − t₀). Одновременно рассчитывался и угол, на который за это же время передвинулась планета, по эпициклу, а в итоге — угол β, под которым из точки T виден радиус эпицикла NP. Долгота определялась суммированием (см. также рис. 19):

λ = Π + M − α + β.

Благодаря «биссекции эксцентриситета» Птолемей сумел и три раза уменьшить погрешность в определении уравнения центра x, при этом также была существенно повышена точность в определении относительного расстояния до планеты (значения r/a). В итоге Птолемей полностью отошел от догмы равномерных круговых движений...

«Тонкости» птолемеевой модели. Прежде всего, поведем речь о Луне. Как уже отмечалось, в движении Луны Птолемей открыл эвекцию: в квадратурах (в первой и третьей четверти) она передвигается на небе, отклоняясь более чем на два своих диаметра от расчетного положения, если при вычислениях учитывалось лишь «первое неравенство». Моделируя движение Луны системой эпицикл — деферент, можно предположить, что в квадратурах она находится ближе к наблюдателю, который и видит ее эпицикл под большим углом. Птолемею следовало учесть открытое Гиппархом вращение линии апсид и тот факт, что Луна возвращается к апогею (и тогда ее скорость имеет наименьшее значение) за T_α = 27,555 суток; этот промежуток времени назван аномалистическим месяцем.

В теории Птолемея Луна движется по эпициклу радиусом b = 51⅙R_⊕ по часовой стрелке и делает полный оборот на нем за T_α, «средняя Луна» движется по деференту радиусом A = 48⅚R_⊕ против часовой стрелки с периодом, равным синодическому месяцу. Центр же деферента находится на расстоянии s = 10⅙R_⊕ от Земли и вращается вокруг нее с тем же периодом по часовой стрелке (рис. 22). Таким образом, наибольшее расстояние до Луны в сизигиях, когда к тому же Луна находится в апогее, равно A + s + b = 64⅙R_⊕, в квадратурах же оно может быть в пределах от A − s + b = 43⅙R_⊕ до A − s − b = 33⅙R_⊕, т. е. может быть почти вдвое меньше, чем в сизигии. Но Птолемею, очевидно, важно было дать метод расчета положения Луны на небе. Поэтому он лишь между прочим указал, что когда Луна находится ближе, то наблюдатель не может охватить взором всей величины ее диаметра.

Рис. 23. Отсчет аномалии M в системе Птолемея

К тому же, как установил Птолемей, аномалию M, которой определяется положение Луны на эпицикле, следует отсчитывать от переменного апогея — от точки H, определяемой направлением от точки Q, находящейся (рис. 23) на диаметрально противоположной стороне окружности, описываемой центром деферента C.

Не менее сложна и теория движения планет. Как отметил Птолемей, Гиппарх в свое время «ограничился лишь тем, что собрал наблюдения для их будущего использования и доказал при их помощи, что гипотезы современных ему астрономов могут быть согласованы с этими наблюдениями». Можно вспомнить также высказывание древнегреческого писателя Плутарха (ок. 46 — ок. 126 гг. н. э.): «До сих пор движения светил преобладали над знаниями математиков»...

Излагая собственную теорию планет, Птолемей в девятой книге «Альмагеста» рассмотрел прежде всего вопрос «о порядке сфер (т. е. орбит) Солнца, Луны и остальных пяти блуждающих светил». Здесь он высказал утверждения, «относительно которых согласны и все древние астрономы», а именно: 1) все планетные сферы расположены ближе к Земле, чем сфера неподвижных звезд, но дальше, нежели сфера Луны, и 2) три сферы — Сатурна, Юпитера и Марса (из которых первая наибольшая, а каждая последующая меньше предыдущей) — лежат за сферой Солнца. Сферы Меркурия и Венеры Птолемей расположил ниже Солнца, поскольку оно «отделяет те из них, которые приходят в противостояние, от тех, которые этого положения не достигают, оставаясь всегда вблизи Солнца».

Для определения угловых скоростей движения планет на эпициклах и скоростей движения центров эпициклов («средних планет») по деферентам Птолемей провел продолжительные наблюдения планет, используя такие промежутки времени, за которые планета, сделав определенное количество оборотов по отношению к Солнцу, возвращалась в то же созвездие (возможно, он в какой-то мере использовал результаты Менелая, автора книги «Сферика», о котором известно, что он в 98 г. н. э. проводил астрономические наблюдения в Риме). В результате Птолемей получил соотношения между числом синодических периодов обращения планет S (обозначены с. п.), годов и дней (г., дн.) и количество полных циклов перемещений планеты среди звезд, т. е. ее обращений (об.):

Сатурн 57 с. п. = 59 г. + 1 3/4 дн. = 2 об. + 1°43′,
Юпитер 65 с. п. = 71 г. − 4 9/10 дн. = 6 об. − 4°50′,
Марс 37 с. п. = 79 г. + 3 13/60 дн. = 42 об + 3°10′,
Венера 5 с. п. = 8 г. − 2 3/10 дн.= 8 об. − 2°15′,
Меркурий 145 с. п. = 46 г. + 1 1/30 дн. = 46 об. + 1°.

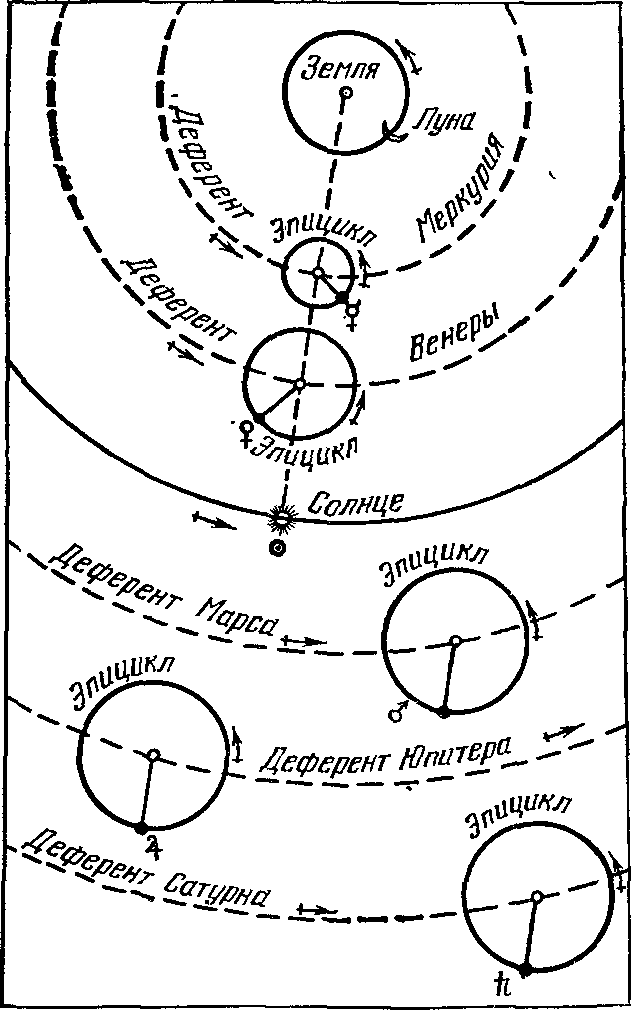
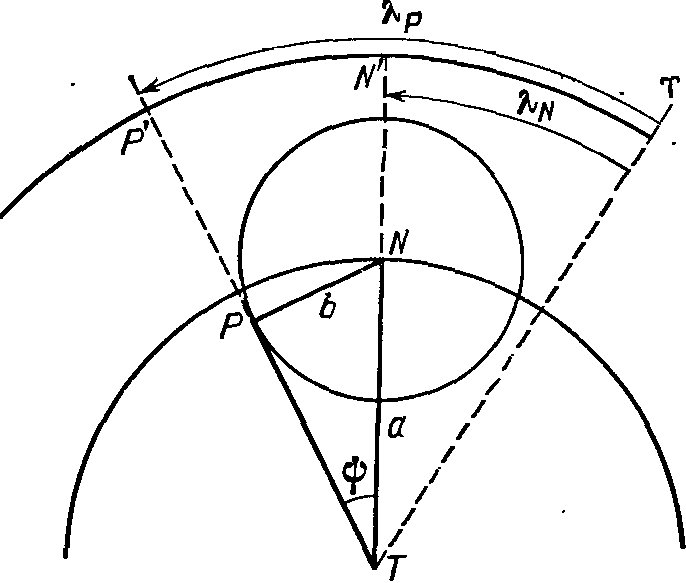
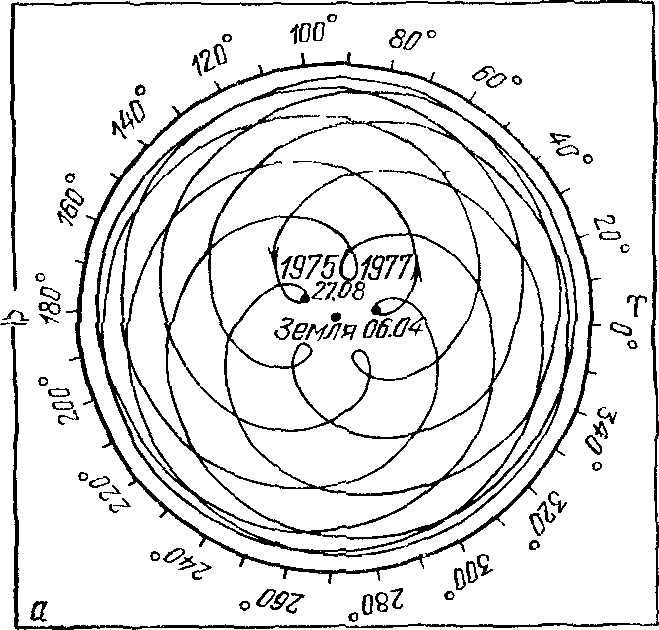
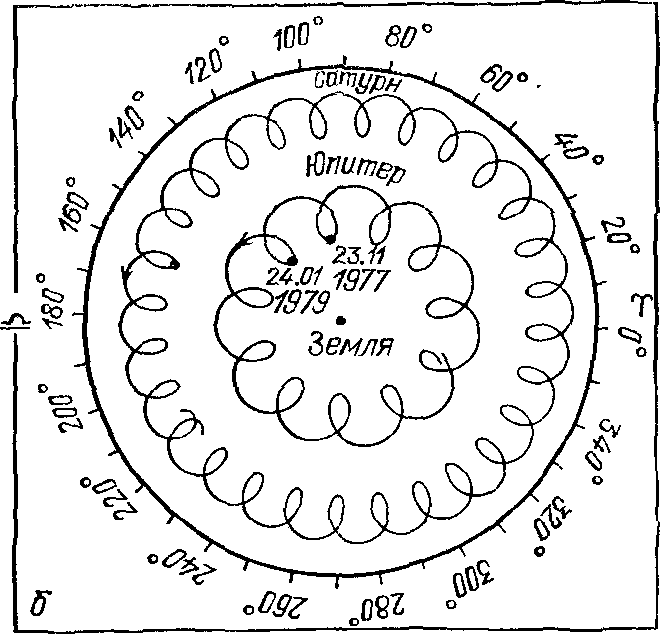
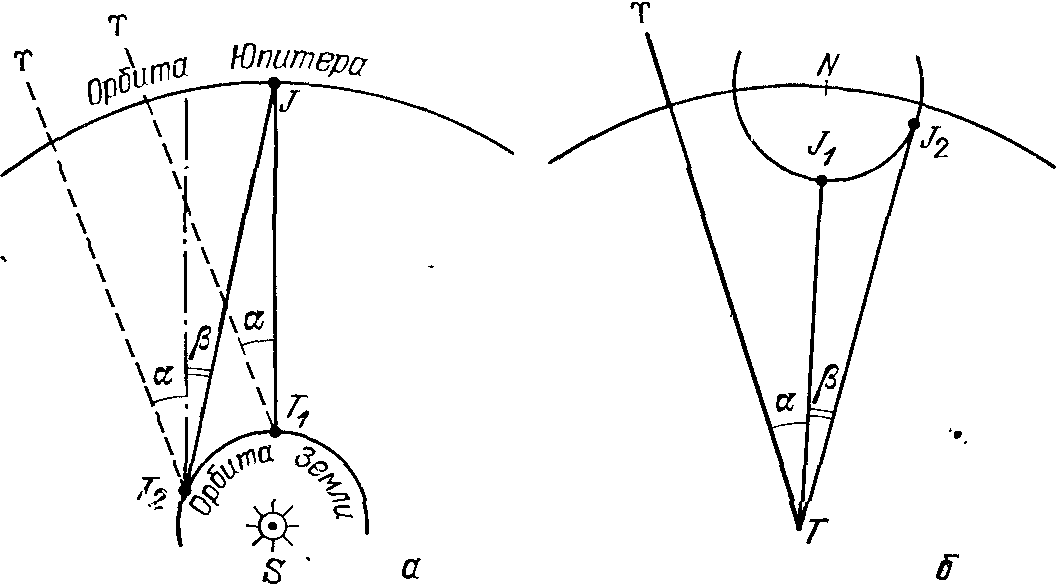
Знак «плюс» означает, что, скажем, для Сатурна 58-е от начала счета противостояние наступило на 1,75 суток позже и на 1°43′ к востоку от исходного, 1-го в счете. Отсюда, кстати, следует, что планета Венера спустя восемь лет практически полностью повторяет свой путь на небе «двумя днями раньше и на 2° западнее, чем в предыдущем цикле».

Если здесь пренебречь небольшими слагаемыми (сутками и градусами), то для верхних планет — Сатурна, Юпитера и Марса — получаем их синодические периоды S = 59/57, 71/65 и 79/37 года соответственно, т. е. 378,07; 398,97 и 779,86 суток. Этими значениями и определяется скорость движения планет по эпициклам (σ = 0,952°, 0,902° и 0,462° в сутки). Для нижних планет — Венеры и Меркурия — S = 8/5 и 46/145 года или соответственно 583,9 и 116 суток, так что скорости их перемещения на эпициклах σ = 0,617° и 3,1° в сутки. Птолемей приводит эти значениями.: Handbuch der Astronomie. — Leipzig, 1913. — Bd. II. — S. 101) с точностью «до сексты градуса» (например, для Сатурна σ = 0°57′7″43‴41^IV43^V40^IV!).

Рис. 24. Система мира по Птолемею

В модели мира Птолемея есть такие особенности (рис. 24):

1) Каждая из верхних планет находится на эпицикле в том же направлении относительно центра эпицикла, в каком относительно наблюдателя находится Солнце. Это значит, что радиус-векторы эпициклов Марса, Юпитера и Сатурна всегда параллельны между собой. Отсюда следует, что, находясь в соединении с Солнцем, планета проходит через апогей, а в противостоянии — через перигей своей орбиты. В том и другом случае истинная планета P проецируется на небесную сферу в ту же точку, что и центр эпицикла («средняя планета») N. Поэтому, разделив число годов, за которое та или другая планета вернулась к той же фазе, скажем, противостоянию, на число полных оборотов, находим периоды обращений «средних планет» (точки N, центра эпицикла планеты) на деферентах: T = 59/2, 71/6 и 79/42 года для Сатурна, Юпитера и Марса соответственно. Им соответствуют средние угловые скорости точки N на деференте ω = 0,033; 0,083 и 0,524° в сутки или соответственно 12,18; 30,34 и 191,35° в год. Птолемей, как и раньше, дает эти величины с точностью до шестой и даже до восьмой 60-й части градуса!

2) Центры эпициклов нижних планет всегда находятся на прямой, соединяющей наблюдателя с Солнцем. Иначе говоря, угловая скорость движения средней нижней планеты ω такая же, как и у Солнца; обозначим ее через μ.

Примечательно, что для каждой из верхних планет выполняется соотношение ω + σ = μ.

Посмотрим теперь, как были установлены для каждой из планет значения β = b/a. Как уже отмечалось, для верхних планет в момент противостояний положения на небе истинной и средней планеты совпадают. Угловая скорость ω средней планеты N известна. Это дает возможность рассчитать ее эклиптическую долготу λ для произвольного момента времени t: λ_N = λ₀+ ωt. Одновременно проводятся измерения долготы λ_P истинной планеты P для установления момента, когда угловое расстояние между истинной планетой P и центром ее эпицикла будет наибольшим: λ_P− λ_N = ψ. В этом положении направления от планеты P на точку N и на Землю (точка T) образуют прямой угол (рис. 25). Если угол ψ известен, то из треугольника PNT находим, что b/a = δ = sin ψ. В частности, для Сатурна ψ = 6°12′ и δ = 0,108, для Юпитера ψ= 11⁰5′ и δ = 0,192, для Марса ψ = 41°12′ и δ = 0,658. Для нижних планет — Меркурия и Венеры — значения δ находятся вообще просто по наибольшей элонгации планеты, и соответственно имеем δ = 0,376 и 0,720.

Рис. 25. К установлению Птолемеем отношения δ радиуса эпицикла к радиусу деферента для верхней планеты

Направление линии апсид, т. е. ориентация деферента как эксцентра в пространстве, определяется путем многократного измерения угла ψ, когда планета проецируется на различные участки неба. Очевидно, что когда она вблизи апогея, этот угол будет наименьшим, около перигея — наибольшим. По величине ускорения в движении средней планеты относительно точки T устанавливается и значение эксцентриситета планеты ε (здесь отметим, что оно вдвое больше введенной позже кеплеровской характеристики эллиптической орбиты: ε = 2e, так как, грубо говоря, им определяется расстояние между фокусами эллипса).

Любознательному читателю предлагаем проверить эффективность разработанного Птолемеем метода: графическим путем определить положение любой из планет для наперед заданной даты при известных начальных параметрах задачи — скажем, долготе планеты в соединении (рис. 26). В «нулевом приближении» можно принять, что эксцентриситет орбиты средней планеты равен нулю (т. е. совместить точки T и O на рис. 21). Очевидно, что если расчет ведется на Δt суток вперед, то необходимо найти угол Γ = σΔt, на который сместится от апогея планета P на эпицикле, и угол M = ωΔt — смещение точки N на деференте, причем полные углы в 360° следует исключить. Отложив сначала угол M, соответствующий положению средней планеты N₂ на момент времени t, рисуем с сохранением относительного масштаба эпицикл и на нем откладываем угол Γ — фиксируем положение планеты P₂. Продолжение линии TP₂ до пересечения с эклиптикой и укажет долготу планеты.

Рис. 26. Графическое определение положения планеты Юпитер на небе по методу Птолемея: соединение Юпитера с Солнцем произошло 13 ноября 1982 г., λJ0 = λ☉0 ≈ 228°; 1 мая 1985 г. (Δt = 900д) долгота планеты λ ≈ 314°, планета находилась в созвездии Козерога

Отметим, что Птолемей учел отклонения планет от эклиптики в процессе их движения среди звезд. Для Марса, Юпитера и Сатурна он ввел углы наклона деферента к эклиптике и эпицикла к деференту. Для Меркурия и Венеры было введено колебание вверх и вниз при помощи небольших вертикальных кругов. Описывая же движение Меркурия, Птолемей пришел к выводу, что деферент этой планеты является овалом, а Земля расположена на большой оси за его центром.

Из-за перемещения планеты по эпициклу расстояние до нее и направление на нее, измеренные от точки весеннего равноденствия, непрерывно изменяются. Изображая эти изменения графически с учетом всего сказанного о величинах ω, σ и δ, получаем гипоциклоиду (рис. 27). Очевидно, что это отображение истинного движения планеты, как ее на самом деле видит наблюдатель с Земли. Конечно, здесь возникает вопрос: как можно получить правильный результат в предвычислении положений планеты на небе, исходя из ошибочного представления о том, что Земля неподвижна и находится в центре мира. Но дело-то в том, что каждое движение относительно (рис. 28). Эпицикл той или другой планеты и есть отображение истинного движения Земли.

Рис. 27. Движение планет относительно Земли: Венеры (а), Юпитера и Сатурна (б); картина движения Венеры на небе повторяется через 8 лет (см. с. 63), и в тех же точках планета была 25.08.1983 и 03.04.1985 гг.; положение Сатурна отмечено на 01.03.1979 г.

В последней, тринадцатой книге Птолемей говорит: «Пусть никто, глядя на несовершенство наших человеческих изобретений, не считает предложенные здесь гипотезы слишком искусственными. Мы не должны сравнивать человеческое с божественным... Просто небесные явления нельзя рассматривать с точки зрения того, что мы называем простым или сложным, так как у нас — все произвольно и переменно, а у небесных естеств — все строго и неизменно, так что их движения по орбитам нельзя представлять себе вынужденными и трудными...».

Рис. 28. Относительность движения на примере Юпитера: смещение Земли на орбите от J1 к T2 (а) приводит к тому же наблюдаемому эффекту, что и передвижение Юпитера на эпицикле от точки J1, к J2 (б): угловое расстояние планеты от точки γ увеличивается на угол β

...Римский философ Сенека (ок. 3 г. до н. э. — 65 г. н. э.) сформулировал важный для науки вопрос так: «Важно было бы исследовать, мир ли вращается вокруг Земли, которая остается неподвижной, или Земля вертится, тогда как мир стоит. Находятся люди, которые утверждают, что нас несет природа, а мы того совершенно не замечаем, что восход и закат светил происходит не от движения неба, а от того, что мы сами то восходим, то заходим относительно их восхождения на небесном своде. Эта задача достойна наших размышлений, ибо мы должны знать, в каком состоянии мы находимся: обрекла ли судьба нашу Землю на вечный покой, или же, наоборот, она одарила Землю быстрым движением; заставили ли боги все небесные тела двигаться вокруг нас, или же мы сами около них вращаемся». Мы уже видели, как ответил на этот вопрос Птолемей. И, кажется, в последующие 1000 лет лишь индийский астроном Ариабхата (476— ?) высказал догадку, что вращение небес — явление кажущееся, что оно обусловлено вращением Земли вокруг своей оси. Да еще «под занавес» первого тысячелетия несколько астрономов из стран ислама будут думать так же...

«Телескопы» времен Птолемея. В «Альмагесте» Птолемей описывает несколько приборов, с помощью которых он и другие древние астрономы проводили наблюдения — определение угловых расстояний между светилами. Прежде всего это «полуденный круг», с помощью которого измерялся наклон эклиптики к экватору и определялось положение Солнца на эклиптике. Прибор состоял из металлического кольца произвольного радиуса, разделенного на 360° и устанавливаемого на надежной подставке вертикально в плоскости меридиана. К этому кольцу прикреплялось меньшее кольцо, на котором в диаметрально противоположных точках устанавливались визирные площадки. При наведении на Солнце верхняя площадка отбрасывала тень на нижнюю, а имеющиеся указатели позволяли отсчитывать угол на шкале большого кольца.

Рис. 29. Квадрант

Если в центре «полуденного круга» установить острие перпендикулярно к плоскости круга, то тень от острия будет падать на северную, нижнюю часть проградуированного кольца. Иначе говоря, для измерений достаточно нанести градусные деления лишь на одну четверть кольца. В этом и состоит принцип работы квадранта, также описанного Птолемеем. Плита с проградуированной четвертью круга устанавливалась в меридиональной плоскости. Высоту Солнца над горизонтом в полдень указывала падающая на шкалу тень от острия. Известно, что со временем квадрант стал одним из самых надежных угломерных инструментов. Его «укрепляли» на стене, ориентированной строго в направлении с севера на юг, или на столбе. Тогда же важнейшими деталями квадранта стали два визира: один располагался в центре дуги, другой (с указателем) скользил вдоль нее (рис. 29).

Рис. 30. Армиллярная сфера

Для измерения эклиптических координат Луны и звезд Птолемей сконструировал прибор астролабон, который со временем был назван армиллярной сферой, или армиллой. Важнейшей частью этого прибора (рис. 30) были два взаимно перпендикулярных и неподвижно скрепленных кольца. Первое из них изображало эклиптику, второе — круг солнцестояний, проходящий через точки эклиптики, в которых Солнце находится в дни летнего и зимнего солнцестояний, В середине этих колец размещалось подвижное кольцо, которое могло поворачиваться вокруг двух штифтов, закрепленных в полюсах эклиптики. Угол отклонения этого кольца (долгота) отсчитывался вдоль кольца эклиптики. По внутренней поверхности подвижного кольца скользило плотно пригнанное и проградуированное «кольцо широты», на котором были укреплены два визира. С их помощью кольца долгот и широт и ориентировались на определенное небесное светило.

Рис. 31. Трикветрум

Для измерения высоты Луны над горизонтом (или, что то же самое, ее углового расстояния от зенита) Птолемей использовал «параллактический инструмент» — прибор из трех реек. Одна из них устанавливалась вертикально. На другой, которая одним кондом закреплялась в верхней части первой рейки, были укреплены два визира, с помощью которых эта рейка направлялась на Луну. На третьей рейке, одним концом прикрепленной к нижней части первой, была нанесена шкала, по которой и определялась хорда угла, соответствовавшего зенитному расстоянию Луны (рис. 31). Позже этот инструмент (так называемый трикветрум) широко использовался астрономами Западной Европы.

Рис. 32. Астролябия

Вспомним и еще об одном угломерном приборе тех времен — астролябии, хотя Птолемей в «Альмагесте» о ней не упоминает. Астролябия (рис. 32) — это металлический круг (его диаметр иногда превышал 50 см), на краю которого устанавливалось неподвижное проградуированное кольцо (лимб). К оси инструмента прикреплялась планка (алидада), на которой были установлены визиры (диоптры). Измерение высоты светила над горизонтом выполнялось тремя наблюдателями: один держал астролябию в вертикальном положении, поддерживая ее за приделанную к кругу проушину, второй нацеливал линейку на небесное светило, третий определял на лимбе высоту светила над горизонтом. Этим прибором устанавливали широту места с точностью до нескольких минут дуги.

Примечания

1. Обозначение р происходит от слова pars — часть (имеется в виду количество частей, которых в диаметре круга насчитывается 120); число 84^p51′10″ записывалось еще и так: 84; 51,10.

2. В XVIII в. было установлено, что в определении дня равноденствия Птолемей ошибся на один день, что и стало причиной отмеченной неточности, хотя именно на такую продолжительность года указывал Гиппарх...

3. Сизигиями называются новолуние и полнолуние.

4. Ньютон Р. Преступление Клавдия Птолемея. — М.: Наука, 1985. Здесь мы встречаемся со стремлением доказать, будто практически все наблюдения, на основе которых Птолемей строил свою теорию движения Солнца, Луны и планет, подделаны. В заключение же упомянутой книги Р. Ньютон делает даже вывод, что «Альмагест» ...«нанес астрономии больше вреда, чем любая когда-либо написанная работа, и было бы намного лучше для астрономии, если бы этой книги вообще не существовало», и что поэтому «величайшим астрономом античности Птолемей не является», наоборот, он... «самый удачливый обманщик в истории науки».

5. Паннекук А. История астрономии, с. 173—174.

6. Идельсон Н.И. Этюды по истории небесной механики. — М.: Наука, 1975. — С. 124—204.