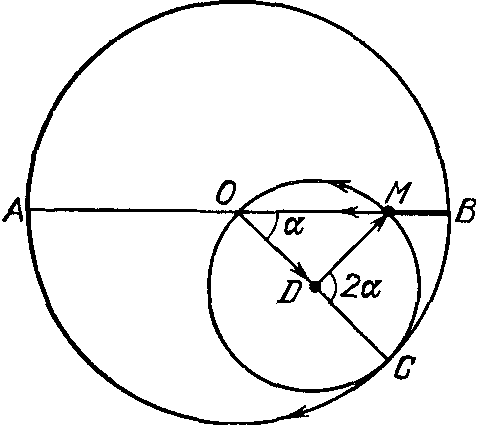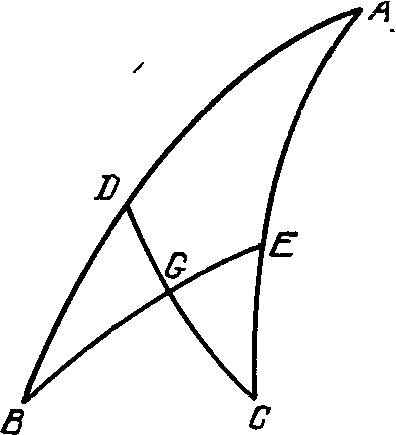
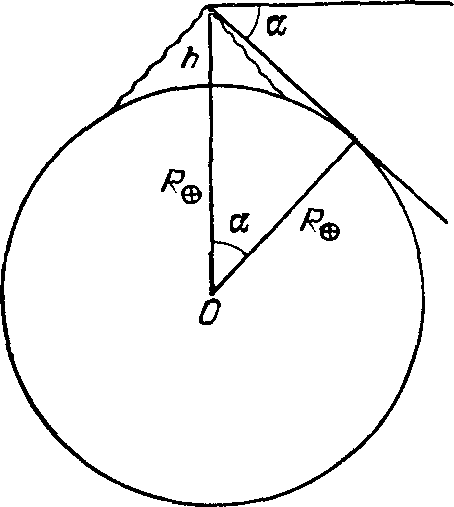
Успехи астрономов стран ислама

Новые очаги культуры. Издавна Аравийский полуостров населяли племена, которые со временем получили название арабов. Объединенные общей религией — исламом, которую основал Мухаммед (ок. 570—632), арабы с середины VII в. начали захват окружающих территорий. В течение ста лет они завоевали Сирию, Иран, Египет, Северную Африку, Пиренейский полуостров и Среднюю Азию. Вначале завоеватели уничтожали памятники науки и культуры покоренных народов. Но очень скоро положение изменилось: они начали усваивать местную культуру, а столица арабского государства Багдад стала центром научной деятельности. В частности, здесь уже в 829 г. (а несколько позже — и в других городах) была создана астрономическая обсерватория.

В странах ислама были основаны университеты: в 755 г. — в Кордове, в 795 г. — в Багдаде, в 972 г. — в Каире. В течение IX в. на арабский язык были переведены труды Аристотеля и других древнегреческих философов, а также «Альмагест» Птолемея.

Рис. 34. Изображение созвездий Девы и Пегаса в одной из копий рукописи ас-Суфи

Вскоре появились «Зиджи» — оригинальные труды исламских астрономов, составленные на основе наблюдений, проведенных в крупных обсерваториях. Это были астрономические таблицы, пользуясь которыми, можно было рассчитать положение планет на небесной сфере. Обязательной составной частью зиджа был свод правил, использованных при составлении таблиц, и правила пользования ими. Порядок расположения материала и характер таблиц во всех зиджах одинаков: 1) о календарях, 2) о движении планет, 3) об определении времени и 4) «об остальных знаниях» (об астрологии). Всего астрономы стран ислама создали несколько тысяч зиджей, учебников, комментариев к зиджам и просто трактатов по астрономии. В зидже помещался также каталог звезд.

В начале IX в. больших успехов добились астрономы Багдада и Дамаска. Так, в 827 г. в долине Сеннаар (Месопотамия) ими при помощи измерительного шнура была измерена дуга меридиана, а наблюдения зенитных расстояний звезд по методу Эратосфена на концах дуги меридиана привели к установлению длины его окружности в 40 700 км в современном исчислении. Тогда же по измерениям долготы Регула после сравнения результата с данными Гиппарха было получено новое значение постоянной прецессии, 1° за 66 лет. Арабские астрономы также обнаружили, что угол наклона эклиптики к экватору несколько меньше значения, которое дал Птолемей, а апогей солнечной орбиты переместился по сравнению с данными «Альмагеста». Имен этих астрономов, начавших свою работу во времена правления халифа аль-Маммуна (813—833), мы почти не знаем. Известно, однако, имя одного из первых переводчиков труда Птолемея на арабский язык: им был Ибн Юсуф (786—833); это он назвал книгу «Китаб аль-маджисти» — «Величайшее сочинение», откуда и пошло привычное для нас название «Альмагест».

А вот несколько астрономов, трудившихся в Багдаде во второй половине IX в., стали позже известны и в Европе. Один из них, Ахмед аль-Фаргани, — Альфраганус, автор «Элементов астрологии». Сабит ибн Корра (836—901) к восьми сферам Птолемея прибавил девятую — «перводвигатель», он же осуществил исключительно точный и квалифицированный перевод «Альмагеста» с греческого языка на арабский (Ибн Юсуф сделал перевод с сирийского языка). В трактатах «О солнечном годе» и «О движении восьмой сферы» Сабит Ибн Корра изложил результаты своих определений параметров орбиты Солнца, привел новое значение прецессии — 49″39‴ (т. е. 49,65″) за год или 1° в 72,5 года. Из анализа наблюдений Гиппарха и Птолемея Ибн Корра впервые сделал вывод, что наблюдения последнего, относящиеся к видимому движению Солнца, были проведены с низкой точностью. Много усилий он приложил для того, чтобы разработать новую теорию трепидации, в которой прецессионное движение не является равномерным, а представляет собой периодическое колебательное движение с амплитудой 4° и периодом в 4000 лет.

Большую известность в Западной Европе получили труды Абу Абдаллаха Мухаммада ибн Джабир аль-Баттани (ок. 850—929). Этот ученый с высокой точностью определил длину тропического года, величину эксцентриситета солнечной орбиты, открыл перемещение солнечного апогея относительно звезд. «Астрономические таблицы», содержавшие и координаты 533 звезд, были изданы в 1537 г. в Нюрнберге и в 1645 г. в Болонье. Аль-Баттани утверждал, что наука звезд следует сразу же за религией, так как является наиболее благородной и совершенной из наук, украшающей ум и формирующей интеллект...

Шедевром средневековой наблюдательной астрономии называли «Книгу неподвижных звезд» выдающегося астронома Абд ар-Рахмана ас-Суфи (903—986). На материале собственных наблюдений ас-Суфи (это прозвище означает «мудрец») проверил и уточнил каталог звезд Птолемея, исправил погрешности, допущенные его арабскими предшественниками; указанные в каталоге ас-Суфи звездные величины звезд были результатом его оригинальных наблюдений. В упомянутом труде ас-Суфи подробно и систематически изложил сведения о древнеарабской астрономии, передал названия созвездий и звезд, использовавшихся арабами доисламского периода, в том числе 28 «стоянок Луны» (маназил), по которым они определяли положение Луны на небе в любой день месяца. В частности, о звездах из созвездия Водолея ас-Суфи пишет: «Арабы называют 2-ю и 3-ю, которые находятся на правом плече, Счастьем Владыки или Государства. Они называют 4-ю и 5-ю, которые расположены на левом плече, вместе с 28-й, которая находится на хвосте Козерога, Счастьем Счастий; это двадцать четвертая стоянка Луны... когда они восходят, начинаются дожди, а когда заходят, прекращаются нездоровые ветры, увеличивается плодородие и падает роса». Для облегчения при отождествлениях звезд книга ас-Суфи была искусно иллюстрирована (рис. 34).

Начала сферической тригонометрии. В XIII главе первой книги «Альмагеста» Птолемей приводит доказательство нескольких теорем плоской и сферической тригонометрии. Среди них — теорема для «полного четырехсторонника» ABCD, известная как теорема Менелая (рис. 35):

хорда (2 CE)/хорда (2 AE) = хорда (2 CG)/ хорда (2 DG) · хорда (2 DB)/хорда (2 AB),

причем все стороны «четырехсторонника» являются дугами больших кругов. Главным образом на основе этого соотношения Птолемей и проводил все свои вычисления. Позже индийские математики заменили хорды синусами, и теорема Менелая приобрела вид

sin CE/sin AE = sin CG/sin DG · sin DB/sin AB.

Уроженец Хорезма, долгое время живший в Багдаде Мухаммад ибн Муса ал-Хорезми (ок. 783 — после 847), автор сочинения (847 г.) «Китаб аль-джабр ва-л-мукабала» («Книга противоположения и восстановления», т. е. перенесения отрицательного члена из одной части уравнения в другую и приведения подобных; отсюда «алгебра») впервые в математике стран ислама использовал тригонометрическую функцию синус и составил таблицы синусов через 1° аргумента. Работавшему же вместе с ним в Багдаде ал-Хабашу ал-Хасибу уже были известны тангенс («первая», или «обращенная» тень — ведь функция «в явном виде» присутствует в задаче о длине тени гномона) и котангенс («вторая», или «плоская» тень), он же ввел и понятие косеканса («диаметра тени» — гипотенузы прямоугольного треугольника, катетами которого являются высота гномона и длина тени).

Рис. 35. Четырехсторонник, дли которого была′ известна широко использовавшаяся Птолемеем теорема Менелая

И вот, наконец, пришла пора заменить теорему о полном четырехстороннике формулой для сферического треугольника АВС со сторонами а, b, c, противолежащими соответственно углам A, B, C:

sin A/sin a = sin B/sin DG · sin DB/sin AB.

Эта теорема синусов была независимо доказана тремя учеными: спор о приоритете долго вели Ибн Ирак (ок. 961 — ок. 1036), Абу-л-Вафа ал-Бузджани (940—998) и Абу Махмуд ал-Худжанди (ум. ок. 1000 г.). В то же время была установлена и теорема тангенсов,

tg b = sin a − sin B,

а в делом родилась сферическая тригонометрия как наука о решении сферических треугольников.

Основы плоской и сферической тригонометрии ал-Бузджани изложил в своем фундаментальном труде «Книга извлечения дуг». Он составил таблицы синусов и тангенсов через каждые 10′. В «Усовершенствованном зидже» он, кстати, дает величину прецессии 1° за 70 лет и 4 месяца. Его ученик Ибн Юнис (950—1009), работая в Каирской обсерватории, составил «Гакемитские таблицы» — таблицы положений Солнца, Луны и планет, которые пользовались популярностью в течение двух веков.

Абу Райхан Бируни. Выдающийся мыслитель, подлинный энциклопедист, изумляющий всех широтой своих научных интересов, Абу Райхаи Бируни (Беруни) родился в 973 г. в предместье г. Кят (сейчас г. Бируни), бывшего в то время столицей Хорезма, крупным культурным центром Средней Азии. Его учителем был другой выдающийся хорезмиец Ибн Ирак. В 16 лет Бируни уже производил самостоятельные астрономические наблюдения, а в возрасте 21 года с помощью сконструированного им самим инструмента Бируни определил наклон эклиптики к экватору: е = 23°33′45″. Еще год спустя он, едва ли не первым в мире, строит земной глобус (точнее, полуглобус) диаметром 5 м. В 995 г. Хорезм был разорен завоевателями, и Бируни, покинув родину, некоторое время пребывал в г. Рей, недалеко от современного Тегерана. Около 1004 г. он вернулся в новую столицу Хорезма Гургандж, где вел активную научную деятельность вплоть до 1017 г., когда Хорезм перешел под власть Махмуда Газнави. В итоге Бируни попал в столицу нового государства — Газну.

Сопровождая Махмуда Газнави в его походе в Индию, Бируни в итоге пробыл в этой стране долгое время, изучил санскрит и перевел на него, в частности, «Начала» Евклида и «Альмагест» Птолемея, выполнил также несколько переводов с санскрита на арабский язык. Итогом же его пребывания там была фундаментальная книга «Индия», в которой Бируни рассказал об индийской истории, философии, науке, обычаях, религии и этническом составе населения. Увы, «Махмуд уничтожил процветание индийцев и совершил в их стране такие чудеса, из-за которых они словно превратились в развеянный прах и разнесшуюся молву»...

В 1030 г. Махмуд Газнави умер, власть в государстве перешла к его сыну Мас'уду, правившему по 1041 г. Как раз тогда, с 1031 по 1037 г., Бируни создает свой «Канон Мас'уда» — подлинную энциклопедию астрономии. Достаточно сказать, что спустя двести лет, в XIII в., знаменитый арабский географ Якут писал, что «Канон Мас'уда» стер следы всех книг по астрономии и математике, а автор его превзошел Птолемея¹.

Труды Бируни — 150 различных названий, из них более 30 по астрономии — сейчас в основном уже доступны каждому: 1-й том — «Памятники минувших поколений» — издан в Ташкенте еще в 1957 г., 5-й том в двух частях — «Канон Мас'уда» — там же в 1973 г. (ч. 1) и 1976 г. (ч. 2). Состоит «Канон» из одиннадцати книг. В книгах I и II Бируни подробно излагает календарные системы, использовавшиеся различными народами, приводит хронологические таблицы. В книге III даны важнейшие тригонометрические теоремы и их доказательства, описываются методы построения правильных многоугольников и др. В книге IV изложены основы сферической астрономии. Здесь Бируни приводит значение определенного им наклона экватора к эклиптике ε = 23°34′0″ (истинное значение в то время было 23°34′45″). В книге V изложены различные вопросы геодезии и математической географии. В частности, здесь приводятся результаты Бируни по определению радиуса Земли (см. ниже). Далее, в книге VI обсуждается движение Солнца, в частности «О том, что апогей Солнца подвижен», и делается вывод, что он передвигается на один градус примерно за 60 лет. В книге VII изложена теория движения Луны, в книге VIII — теория затмений и отдельно (это было крайне важно для исповедующих ислам!) «О наблюдении молодого месяца». В книге IX даны сведения о неподвижных звездах, приведен каталог 1029 звезд с их координатами и звездными величинами по Птолемею и ас-Суфи. Прецессию Бируни определил в 54″10‴ за год или 1° в 69 лет. В книге X изложена теория планетных движений, в книге XI — «искусство приговоров звезд», т. е. элементы астрологии.

В целом «Канон Мас'уда» построен по образцу «Альмагеста» и в духе геоцентризма. Бируни, конечно, знал о взглядах «пифагорейцев» и, признавая в принципе возможность вращения Земли вокруг оси, даже рассчитал скорость движения точки экватора и получил «3778 локтей за 4 секунды часа», что при длине локтя в 49,43 см дает 466 м/с. По-видимому, это значение показалось Бируни очень большим, да и общие физические представления того времени, вероятно, казались ему вполне совместимыми с представлением о неподвижности Земли. Во всяком случае, в «Каноне Мас'уда» он рассуждает в духе геоцентризма. Но сам же Бируни упоминает, что «видел одного из выдающихся ученых в области астрономии, который был склонен защищать эту точку зрения». Возможно, это был Абу Са'ид ас-Сиджизи, у которого Бируни видел «челночную астролябию», основанную на моделировании вращения Земли.

Рис. 36. К определению радиуса Земли методом измерения угла понижения горизонта

Как сообщает Бируни, в его время в вопросе о размерах Земли были «большие расхождения во мнениях». Поэтому «группа ведущих данного искусства» определила, что «на один градус... приходится 56⅔ мили». При длине мили в 1,973 км это дает 111,804 км на 1° дуги земного меридиана. Бируни пишет: «Моим огромным желанием было самому выполнить все это... я нашел в земле индийцев гору, возвышающуюся над пустыней... я измерил с вершины этой горы [угол к линии], где на взгляд небо встречается с Землей... и я нашел, что [горизонт] понижается... немного меньше, чем на треть с четвертью градуса, и принял эту величину за 34′. Я определил высоту горы, наблюдая высоту ее вершины с двух мест... и нашел, что она равна 652 с половиной одной десятой локтя». Далее решение сводится к соотношению

R⊕ = (h cos α)/(1 − cos α), (1.5)

где h — высота горы, α — угол понижения горизонта (рис. 36). Так, Бируни нашел для 1° дуги 56,1 мили = 110,685 км, радиус же Земли R⊕ = 6345 км.

Радиусы планет и радиусы планетных сфер, определенные Бируни в «Каноне Мас'уда», приведены в табл. 1.

Насколько известно, Бируни первым построил неподвижный (настенный) квадрант радиусом 7,5 м, на котором проводил точные (до 2′) наблюдения Солнца и планет. В течение 400 лет этот инструмент оставался крупнейшим в мире. Умер Бируни 11 декабря 1048 г.

Здесь уместно отметить, что мусульманские астрономы придавали особенное значение вопросу о точности наблюдений. Иногда наблюдения записывались в протокол, засвидетельствованный общей присягой нескольких астрономов и юристов. Вероятно, это делалось в случаях, когда результаты наблюдений предполагалось использовать для календарных расчетов или для астрологических предсказаний.

Таблица 1. Радиусы планет и планетных сфер по Бируни (в единицах радиуса Земли R⊕ = 1)

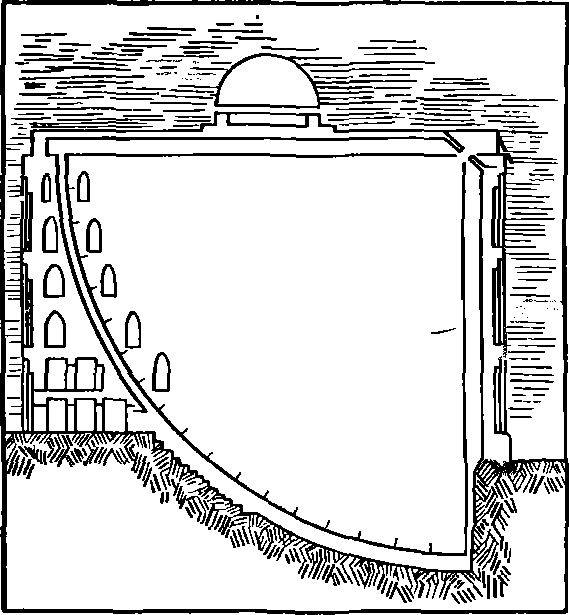
От Кордовы до Самарканда. В X—XII вв. значительных успехов достигли астрономы, работавшие в магометанской части Испании. Известно, что около 970 г. в г. Кордове была организована академия с большой библиотекой. В частности, астроном аз-Заркали, известный под именем Арзахеля (1029—1087), усовершенствовал астролябию и опубликовал «Толедские таблицы» положений планет.

В то время арабские астрономы уже пришли к выводу, что теория Птолемея плохо согласуется с наблюдениями. Известный философ Мухаммед ибн Рушд, или Аверроэс (1126—1198), и его сторонники пришли к выводу, что движение вокруг любого центра возможно лишь в том случае, если в центре находится какое-либо неподвижное тело, а не воображаемая движущаяся точка. Еврейский ученый Мозес бен Маймон, или Маймонид (1135—1204), как и марокканский астроном аль-Битруджи (ум. ок. 1204 г.) отвергали теорию эпициклов. Аль-Битруджи в «Принципах астрономии» пытался возвратиться к идеям Евдокса, полагая, что все небесные тела обращаются вокруг Земли, но движутся они с востока на запад с различными скоростями. Быстрее всего — за сутки — вращается сфера звезд. Что же касается других, то их движение тем медленнее, чем ближе к Земле расположена планета.

В середине XIII в. Испания была освобождена от арабов, а библиотека Кордовы сожжена. Кстати, это было едва ли не правилом — сжигать все мусульманские библиотеки! Так, известно, что в одной Гренаде тогда было сожжено 24 000 книг...

В 1258 г. сын Чингис-хана Хулагу буквально стер с лица земли Багдад (опять же были преданы огню ценнейшие рукописи), но создал крупный научный центр и астрономическую обсерваторию в г. Марага (теперь — Иранский Азербайджан). Строительство обсерватории и наблюдения на ней проводились под руководством Насирэддина ат-Туси (1201—1274). Примечателен разговор между ат-Туси и Хулагу, решивший вопрос об ассигновании крупной суммы в 20 000 динаров на это строительство. Хулагу спросил: «Разве наука о звездах так полезна, что стоит тратить огромную сумму на обсерватории?» В ответ ат-Туси сказал: «Позвольте поступить так: пусть в полной тайне кто-нибудь поднимется на эту гору и спустит оттуда большой пустой таз, но чтобы об этом никто не знал». Таз произвел большой шум, среди войска поднялась паника, Хулагу-хан и ат-Туси оставались спокойными. После этого ат-Туси сказал хану: «Мы знаем причину шума, а войска не знают; мы спокойны, а они волнуются. Так же, если будем знать причины небесных явлений, мы будем спокойны на земле»...

Среди многочисленных инструментов обсерватории, которая располагалась на высоте более 1600 м над уровнем моря, главным был квадрант радиусом 3¼ м. Число сотрудников обсерватории, среди которых были выдающиеся астрономы, достигало 100. Итогом 12-летних наблюдений марагинских астрономов был «Зидж Ильхани» — «Ильханские таблицы», использовавшиеся в дальнейшем на протяжении многих лет для составления ежегодных календарей. Здесь же было дано наиболее точное значение прецессии — 51,4″ в год.

Из всего сказанного ранее о системе мира Птолемея видно, что ее создатель отошел от основного принципа, «завещанного» Платоном, — принципа равномерных круговых движений: движение «средней планеты» по деференту для находящегося в центре мира наблюдателя не является равномерным. И как только трудности с согласованием сделанных на протяжении более чем тысячелетий наблюдений планет в рамках теории Птолемея стали очевидными, астрономы стран ислама — и в том числе ученые марагинской обсерватории — сделали попытки перейти к новым моделям мира. Они, как уже было сказано, отвергали эпициклы, стремились возродить систему гомоцентрических сфер Евдокса... Насирэддину же удалось построить модель такого движения, в котором условие его равномерности выполнялось при удовлетворительном согласии с данными наблюдений. Достигнуто это было опять-таки определенной комбинацией круговых движений. Сама же модель изложена ее автором в «Памятке по астрономии».

Составным элементом теории является следующая «лемма ат-Туси». Пусть круг диаметра OC = d катится с угловой скоростью со по окружности большого круга диаметра AB = 2d, касаясь его внутренним образом и обращаясь в то же время вокруг собственного центра с угловой скоростью 2ω в направлении, противоположном направлению качения. Тогда произвольная точка окружности малого круга, перемещаясь от своего начального положения — точки касания, будет совершать прямолинейное движение вдоль диаметра большого круга (рис. 37).

Рис. 37. «Пара Туси»: из вращательного движения двух окружностей можно получить поступательное движение точки M вдоль диаметра; это эквивалентно вращению двух векторов равной длины с угловыми скоростями ω⃗ и −2ω⃗ со длина результирующего вектора изменяется по закону OM⃗ = OB⃗ cos ωt

Как видно, из сложения двух круговых движений ат-Туси получает прямолинейное движение. В терминологии векторного исчисления и теории механизмов оно описывается парой векторов равной длины, вращающихся с постоянной скоростью, причем скорость второго вектора вдвое больше скорости первого и направлена в противоположную сторону. Конец же второго вектора совершает простое гармоническое колебание, так что длина результирующего вектора периодически изменяется от нуля до 2d. Позже «пару Туси» использовал Коперник для описания движения Меркурия. Это, кстати, частный случай гипоциклоид: при соотношении между радиусами большого и малого кругов R = nr имеем гипоциклоиды с заострениями, если n — целое число, самопересекающиеся эпициклоиды, если n дробное, и незамыкающиеся эпициклоиды, если n иррациональное.

Читателю, интересующемуся этим вопросом, можно посоветовать ряд книг и статей, где проводится соответствующий анализ². Действительно, «пара Туси» обеспечивает изменение длины результирующего вектора, т. е. построение эксцентра. Однако для объяснения неравномерного движения планет ат-Туси все же сохранил эквант в смысле «выравнивающей точки». Следующий шаг вперед (если это было движение вперед...) сделал Ибн аш-Шатир (1304—1376), представивший движение Луны с помощью деферента и двух эпициклов. Позже такая модель была подробно разработана Николаем Коперником (см. далее рис. 41); знал ли он о работе аш-Шатира, неизвестно.

Но своей моделью ат-Туси сделал все же очень многое: он впервые как бы перечеркнул противопоставление двух видов движения — «совершенного» кругового и «местного» прямолинейного...

И, наконец, выдающимся научным астрономическим центром во времена 40-летнего правления внука Тимура Улугбека (1394—1449) был Самарканд. Здесь в 1424 г. была построена крупнейшая в мире астрономическая обсерватория. Ее трехэтажное здание высотой 30 м размещалось на холме высотой 21 м. Основным инструментом здесь был мраморный секстант радиусом 40 м, который на 10 м углублялся в подземелье (рис. 38). Поскольку одному градусу здесь соответствовала дуга длиной 70,2 см, этот прибор давал возможность производить наблюдения Солнца с точностью до 1″. Итогом работы Улугбека и его сотрудников были «Новые астрономические таблицы», в которых помещены введение (теория) и собственно таблицы. Введение состояло из четырех частей: изложения методов летосчисления, практической астрономии, изложения теории планет и, наконец, астрологии.

Анализ данных Улугбека о продолжительности звездного года и годичного движения планет показывает, что его численные результаты очень близки к современным. Среди таблиц был помещен также каталог, охватывающий 1018 звезд. Анализируя все эти наблюдения, французский ученый Пьер Симон Лаплас (1749—1827) назвал Улугбека «самым выдающимся наблюдателем»...

Особый интерес вызывают взгляды ученых Самаркандской обсерватории по вопросу о месте Земли в мире. Так,

Рис. 38. Самаркандская обсерватори

Казы-Заде ар-Руми в своем произведении «Шарх Джагмини» (1412 г.) писал: «...некоторые ученые считают, что Солнце находится в середине орбит планет. Та планета, которая движется медленнее, чем другая, дальше удалена от Солнца. Ее расстояние будет больше. Наиболее медленно движущаяся планета находится на наибольшем расстоянии от Солнца». И в другом месте: «Земля неподвижна. Центр ее совпадает с центром вселенной. Такая гипотеза наиболее вероятна. Но есть другая гипотеза... Раз каждое тяжелое тело (где бы оно ни находилось) движется по направлению к центру Земли, то можно считать, что центр Земли является только центром тяжелых тел, окружающих Землю. Отсюда можно допускать, что и сам центр Земли движется и вместе с ним движется вся Земля. Такая гипотеза тоже замечательна».

А вот что писал другой сотрудник этой же обсерватории Абд ал-Али ал-Кушчи (ум. в 1474 г.) в «Комментарии к тезисам теологии»: «Земля движется с запада на восток. Какие доказательства этой теории? Известно, что планеты движутся на восток медленно. Но движение их на запад быстрее. Невозможно предположить, что одно и то же светило одновременно движется по противоположным направлениям. Такое медленное движение можно относить и к самой Земле. Если не будем так говорить, то получается противоречие.

Поэтому считают, что суточное движение светил на запад возникает с действительным движением самой Земли с запада на восток. Поэтому нам кажется, что светила восходят на востоке и заходят на западе. Такое ощущение бывает у наблюдателя, сидящего на корабле, движущемся по реке. Наблюдателю известно, что берег воды неподвижен. Но ему кажется, что берег движется по направлению, противоположному направлению корабля»³.

Стоит ли после этого удивляться тому, что сам Улугбек был обвинен в ереси, что старший его сын, находившийся под влиянием реакционного духовенства, объявил ему войну и что Улугбек погиб от предательской руки как «отступник от ислама»... Составленные под его руководством «Новые Гураганские таблицы» принесли ему немеркнущую славу. Каталог же звезд, входивший в этот труд, был издан в Оксфорде в 1648 г. частично (включены положения всего 98 звезд), а в 1665 г. напечатан полностью. Позже он неоднократно переиздавался с многочисленными комментариями...

Примечания

1. Сираджинов С.Х., Матвиевская Г.П. Абу Райхан Беруни и его математические труды. — М.: Просвещение, 1978. — С. 31.

2. Рамазанова С.А. Восточные средневековые теории движения Луны и планет // Математика и астрономия в трудах ученых Средневекового Востока. — Ташкент: Фан, 1977. — С. 97—107; Григорьян А.Т., Рожанская М.М. Механика и астрономия на средневековом Востоке. — М.: Наука, 1980; Мамедбейли Г.Д. Основатель Марагинской обсерватории Насирэддин Туси. — Баку: Изд-во АН АзербССР, 1961.

3. Джалалов Г.Д. Некоторые замечательные высказывания астрономов самаркандской обсерватории // ИАН. — 1958. — Вып. IV. — С. 382—383.