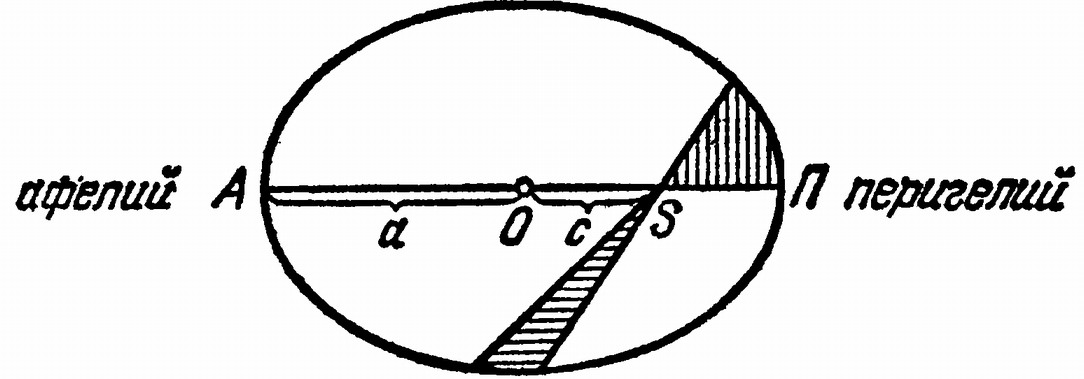
Элементы орбит

Размер орбиты характеризуется величиной большой полуоси эллипса а, выражаемой в астрономических единицах. На рис. 28 — это отрезок ОА или ОП, от центра эллипса до его вершины. Вершина эллипса П, ближайшая к Солнцу S, называется перигелием; здесь планета ближе всего к Солнцу и движется всего быстрее. Противоположная, самая далекая от Солнца точка называется афелием.

Рис. 28. Эллиптическая орбита планеты и второй закон Кеплера. Солнце находится в точке S.

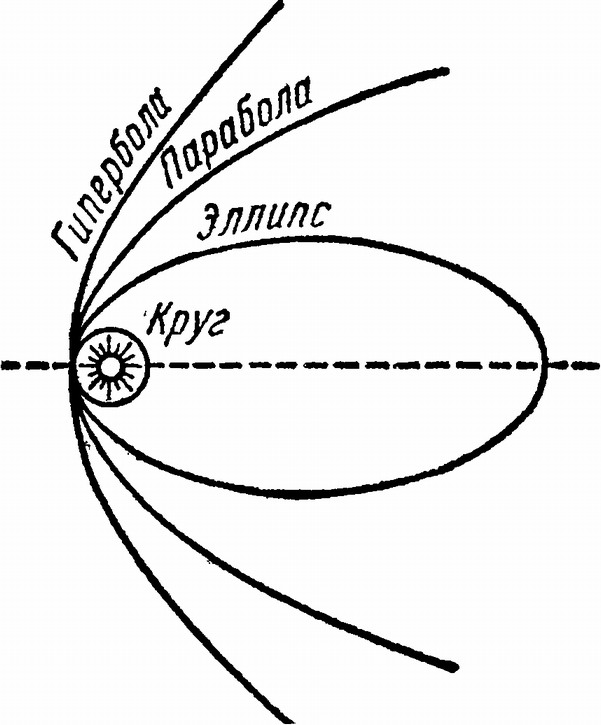
Чем больше вытянут эллипс, тем больше различие между расстояниями планеты от Солнца в перигелии и афелии, тем дальше фокус эллипса отстоит от его центра О. Эту вытянутость эллипса характеризуют эксцентриситетом e, представляющим отношение расстояния от фокуса до центра к длине большой полуоси.

Для окружности e=0, а когда e достигает единицы, то центр эллипса уходит в бесконечность. Иначе говоря, эллипс бесконечно растягивается, так что его ветви стремятся стать параллельными друг другу, и получается незамкнутая кривая, называемая параболой. Еще более разомкнутая кривая называется гиперболой; у нее e больше 1.

Кратчайшее расстояние от Солнца до орбиты, т. е. до ее перигелия, называется перигельным расстоянием.

Третий элемент i — это угол, под которым плоскость орбиты светила наклонена к плоскости земной орбиты (к эклиптике); он называется наклонением. Для планет, которые все движутся около Солнца в одинаковом направлении^ наклонения орбит очень невелики. Если наклонение больше 90° (например, для некоторых комет), то это означает, что направление обращения тела противоположно направлению обращения планет.

Рис. 29. Типы орбит.

Четвертым элементом мы назовем какой-нибудь из моментов, когда светило проходит через перигелий. Его обозначим через T.

Эксцентриситеты орбит больших планет невелики, наибольшие у Плутона: 0,253, затем у Меркурия: 0,206. У Земли эксцентриситет орбиты всего 0,017, или 1/60, и если начертить орбиту Земли с большой полуосью в целый метр, то малая полуось будет всего на 1/7 мм меньше.