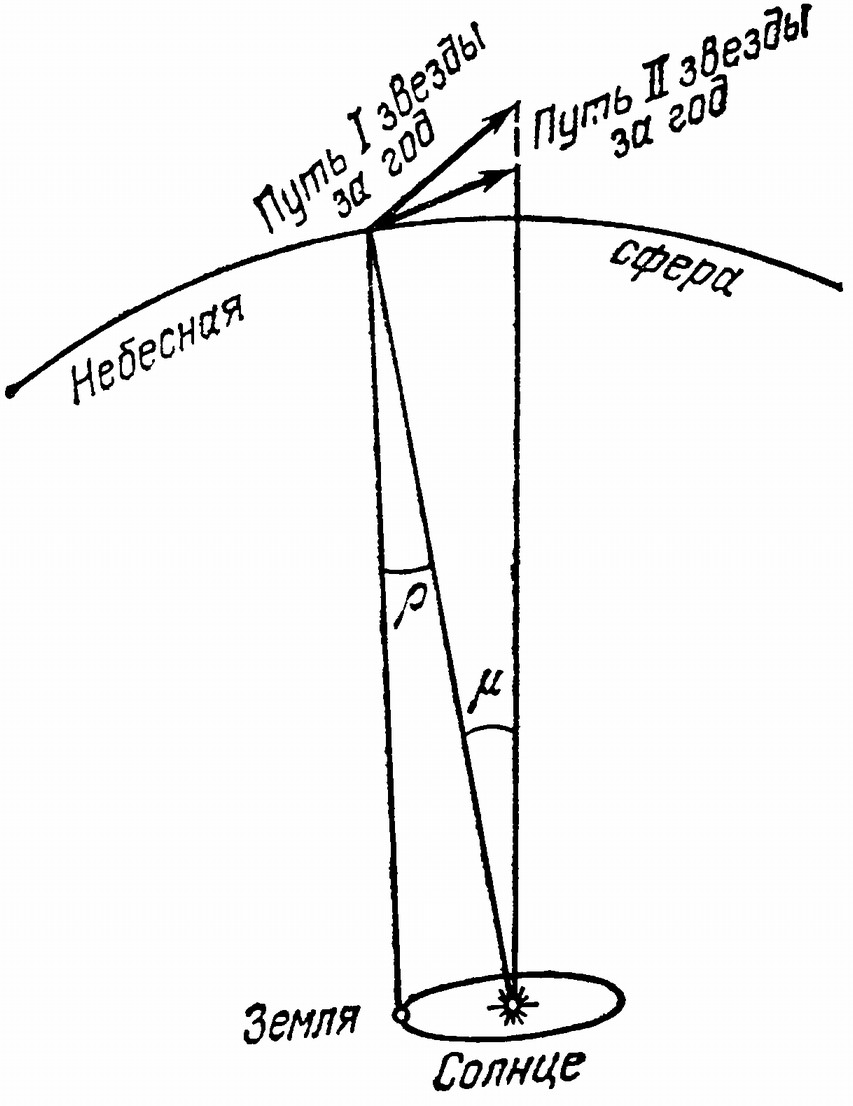
Лот в безднах мироздания

За пределами Солнечной системы к звездам приходится сделать такой большой скачок в расстояниях, что он удался всего лишь 140 лет назад, гораздо позднее, чем исчезли сомнения в подобии между Солнцем и звездами. Измеритель морских глубин, — лот, в области астрономии неоднократно «забрасывался» в направлении разных звезд к долго не мог достигнуть ни одной из них, не мог достать «дна». Это, конечно, лишь фигуральное сравнение, потому что, как и в случае определения температур светил, возможность непосредственных измерений расстояний здесь исключена. Как мы сейчас увидим, их можно найти лишь косвенным путем, вычисляя на основании измерения других величин. Этот путь, указанный еще Коперником, состоит в измерении углов, но приборы и методы, позволяющие достигнуть необходимой точности, были созданы лишь в XIX веке.

Как и при определении расстояния до любого недоступного предмета, идея способа заключается в измерении разности направлений, по которым видна звезда с двух концов базиса известной длины. Расстояние, соответствующее этой разности направлений, можно вычислить с помощью тригонометрии. В данном случае диаметр Земли в качестве базиса оказался слишком мал, и для огромного большинства звезд при современной точности измерения углов даже диаметр земной орбиты недостаточен. Все же именно его Коперник рекомендовал взять за базис, что и выполнили ученые позднейших поколений.

Только 140 лет назад замечательному астроному В.Я. Струве в России, Бесселю в Германии и Гендерсону в Южной Африке удалось произвести достаточно точные измерения и впервые установить расстояния до некоторых звезд. Чувство, испытанное при этом современниками, напоминало радость моряков, которые при долгом плавании безуспешно бросали лот и, наконец, достали им до дна.

Классический способ определения расстояний до звезд состоит в точном определении направления на них (т. е. в определении их координат на небесной сфере) с двух концов диаметра земной орбиты. Для этого надо их определить в моменты, отделенные друг от друга полугодом, так как Земля за это время сама переносит с собой наблюдателя с одной стороны своей орбиты на другую.

Кажущееся смещение звезды, вызванное изменением положения наблюдателя в пространстве, чрезвычайно мало, едва уловимо. Его предпочитают измерять по фотографии, делая для этого, например, на одной и той же пластинке два снимка избранной звезды и ее соседок, один снимок через полгода после другого. Большинство звезд так далеки, что их смещение на небе при этом совершенно незаметно, но по отношению к ним достаточно близкая звезда заметно смещается. Это ее смещение и измеряют с точностью до 0″,01 — большей точности пока достигнуть еще не удается, но она уже намного выше точности, достигнутой шестьдесят лет назад.

Описанное кажущееся смещение звезды вдвое больше того угла, под которым с нее был бы виден радиус земной орбиты и который называется годичным параллаксом. (Мы здесь говорим о радиусе потому, что в данном случае отличием орбиты Земли от окружности можно пренебречь.)

Самой близкой к нам звездой можно считать звезду первой величины ос Центавра, не видимую в СССР, хотя одна близкая к ней, невидимая невооруженным глазом звездочка оказывается еще на 1% ближе. Параллакс этих звезд наибольший и составляет ¾ он измерен с точностью около 1%, поскольку точность угловых измерений достигает 0″,01.

Под углом около 0″,01 нам представляется поперечник копейки, если ее поставить на ребро на Красной площади в Москве и рассматривать из Тулы или из Рязани! Вот какова точность астрономических измерений! Под углом в 0″,01, говоря точно, видна линейка, на которую смотрят под прямым углом с расстояния, в 20 626 500 раз большего, чем длина линейки.

По параллаксу легко узнать соответствующее расстояние. Мы получим расстояние до звезды в радиусах земной орбиты, если разделим число 206 265 на величину параллакса, выраженного в секундах дуги. Чтобы выразить его в километрах, надо полученное число умножить еще на 150000000.

Мы уже знаем, что большие расстояния удобнее выражать в световых годах или в парсеках. Звезда α Центавра и ее соседка, прозванная «Ближайшая», так как она еще чуть-чуть ближе к нам, отстоят от нас в 270000 раз дальше, чем Солнце, т. е. на 4 световых года. Курьерский поезд, идя без остановок со скоростью 100 км в час, добрался бы до нее через 40 миллионов лет! Попробуйте утешиться воспоминанием об этом, если вам когда-либо надоест продолжительная езда в поезде...

Рис. 140. Параллакс и собственное движение звезд. На рисунке параллакс ρ близких одна к другой звезд и их собственные движения μ одинаковы, но их путь в пространстве различен.

Точность измерения параллаксов в 0″,01 не позволяет измерить параллаксы, которые сами меньше этой величины, так что описанный способ неприменим к звездам, отстоящим далее 300—350 световых лет.

Кроме того, легко видеть, что если при параллаксе в 0″,10 ошибка в 0″,01, составит 10%, то при измеренном параллаксе в 0″,01 мы должны допустить, что истинный параллакс может составить и 0″,02 и 0″,00. В первом случае действительное расстояние (соответствующее 0″,02) будет около 150 световых лет, во втором случае оно равно бесконечности. При таких малых параллаксах ошибка в 20% при определении расстояния по спектру делает их более надежными, чем классический способ определения расстояний, на котором, впрочем, они сами основаны. Классическим способом, описанным здесь, за 140 лет определены расстояния до 6000 звезд (около 10000 определений), спектральных же параллаксов за 30 лет определено около 28000. Комментарии, как говорится, излишни.

С помощью описанного способа и других, использующих спектры, а также с помощью совершенно иных косвенных методов можно определять расстояния до звезд, отстоящих гораздо дальше, чем на 300 световых лет. Свет звезд некоторых далеких звездных систем доходит до нас за сотни миллионов световых лет. Это вовсе не значит, как часто думают, что мы наблюдаем звезды, может быть, уже не существующие сейчас в действительности. Не стоит говорить, что «мы видим на небе то, чего в действительности уже нет», ибо подавляющее большинство звезд изменяется так медленно, что миллионы лет назад они были такими же, как сейчас, и даже видимые места их на небе меняются крайне медленно, хотя в пространстве звезды движутся быстро.