Приложение Б¹. Стоунхендж — вычислительная машина каменного века

В своей «Истории древнего мира», написанной примерно в 50 г. до н. э., Диодор Сицилийский [1] говорит о доисторической Британии: «...с этого острова Луна видна так, будто бы она очень близка к Земле, и глаз различает на ней такие же возвышенности, как на Земле. Говорят также, что бог [Луна?] посещает остров каждые 19 лет; это период, за который звезды завершают свой путь по небу и возвращаются на прежнее место... И есть также на этом острове великолепное святилище Аполлона [Солнца], а также прекрасный храм... и хранители святилища именуются Бореадами, и должности эти передаются в их роду из поколения в поколение».

Я признателен английскому археологу Р.С. Ньюэллу за то, что он ознакомил меня с этой классической работой. Диодор получил эти сведения из вторых рук, и их часто игнорировали, принимая за выдумку, но не исключено, что речь здесь идет о Стоунхендже.

Самая северная точка восхода Луны — над камнем D, если смотреть из центра Стоунхенджа (аналогично восходу Солнца в день летнего солнцестояния над Пяточным камнем) [2]. За период в 18,61 года самая северная точка восхода Луны передвинется от D к Пяточному камню, затем к точке F, а потом вернется к D. Таким образом, эта точка из-за отставания узлов лунной орбиты колеблется, как маятник, из стороны в сторону в пределах Аллеи. Если рассматривать какой-либо конкретный восход Луны, например, в полнолуние, ближайшее ко дню зимнего солнцестояния, то полный цикл длится либо 19, либо 18 лет.

Положения Луны были вычислены за период с 2001 по 1000 г. до н. э. с учетом членов только первого порядка, и для каждого зимнего солнцестояния за этот же период были определены азимуты точек восхода Луны. На рис. 1 приведены результаты за период с 1600 по 1400 г. до н. э. Расчеты на IBM 7094 заняли 40 секунд машинного времени.

Можно считать, что лунный цикл равен 19 годам, причем неточность составляет 38%. Например, в день зимнего солнцестояния Луна всходила точно над камнем F в 1671, 1652, 1634, 1615 и 1596 гг. до н. э., то есть интервалы составляют 19, 18, 19 и 19 лет. За период с 2001 по 1000 г. до н. э. в дни зимних солнцестояний над камнем F Луна восходит 52 раза, причем, как показано в табл. 1, 32 интервала равны 19 годам, а 20 интервалов — 18 годам. Аналогичный лунный цикл для камня D также чаще равен 19 годам (табл. 1).

Таблица 1. Интервалы в годах между восходами зимней Луны над камнями D, F и Пяточным камнем

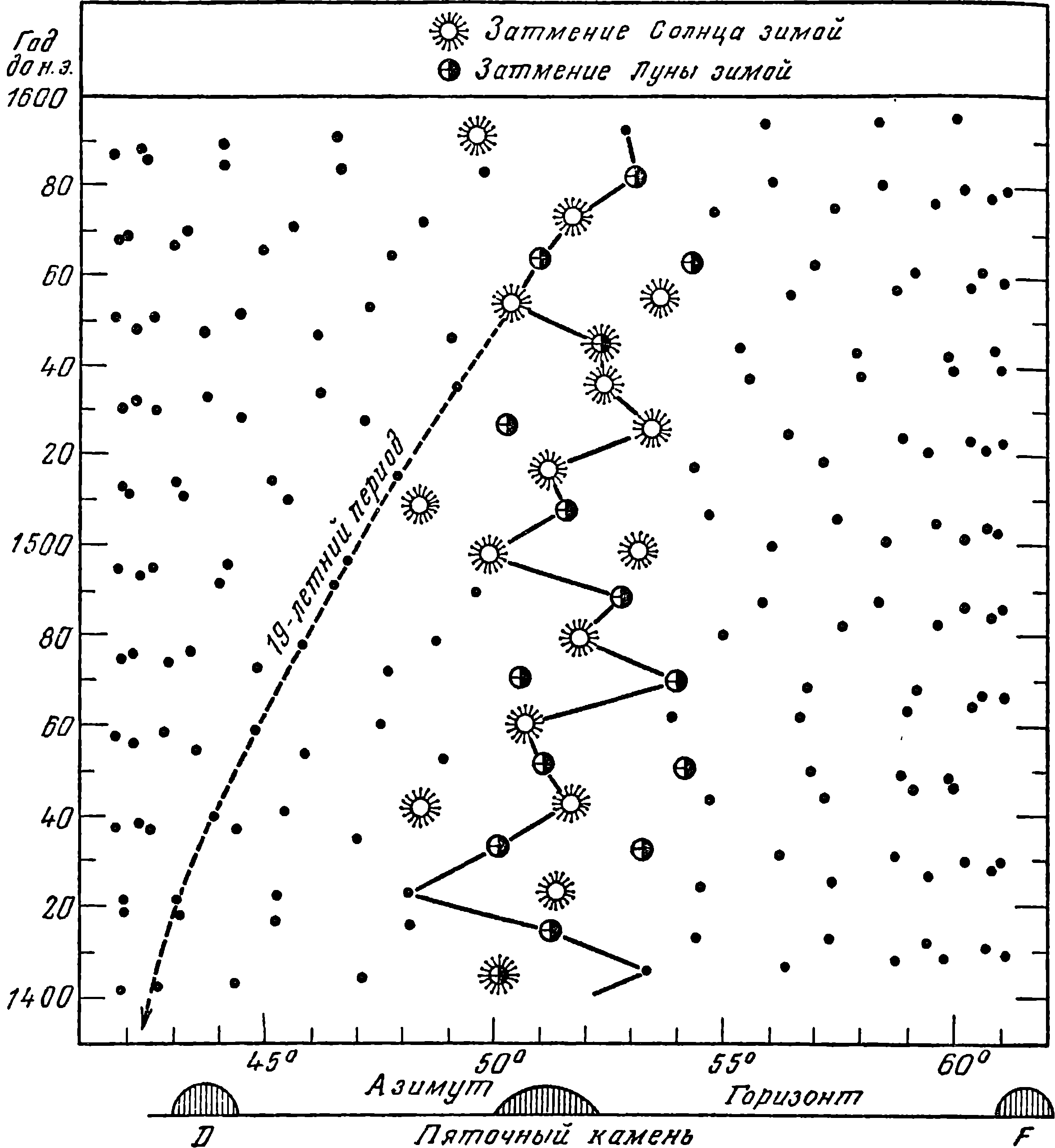
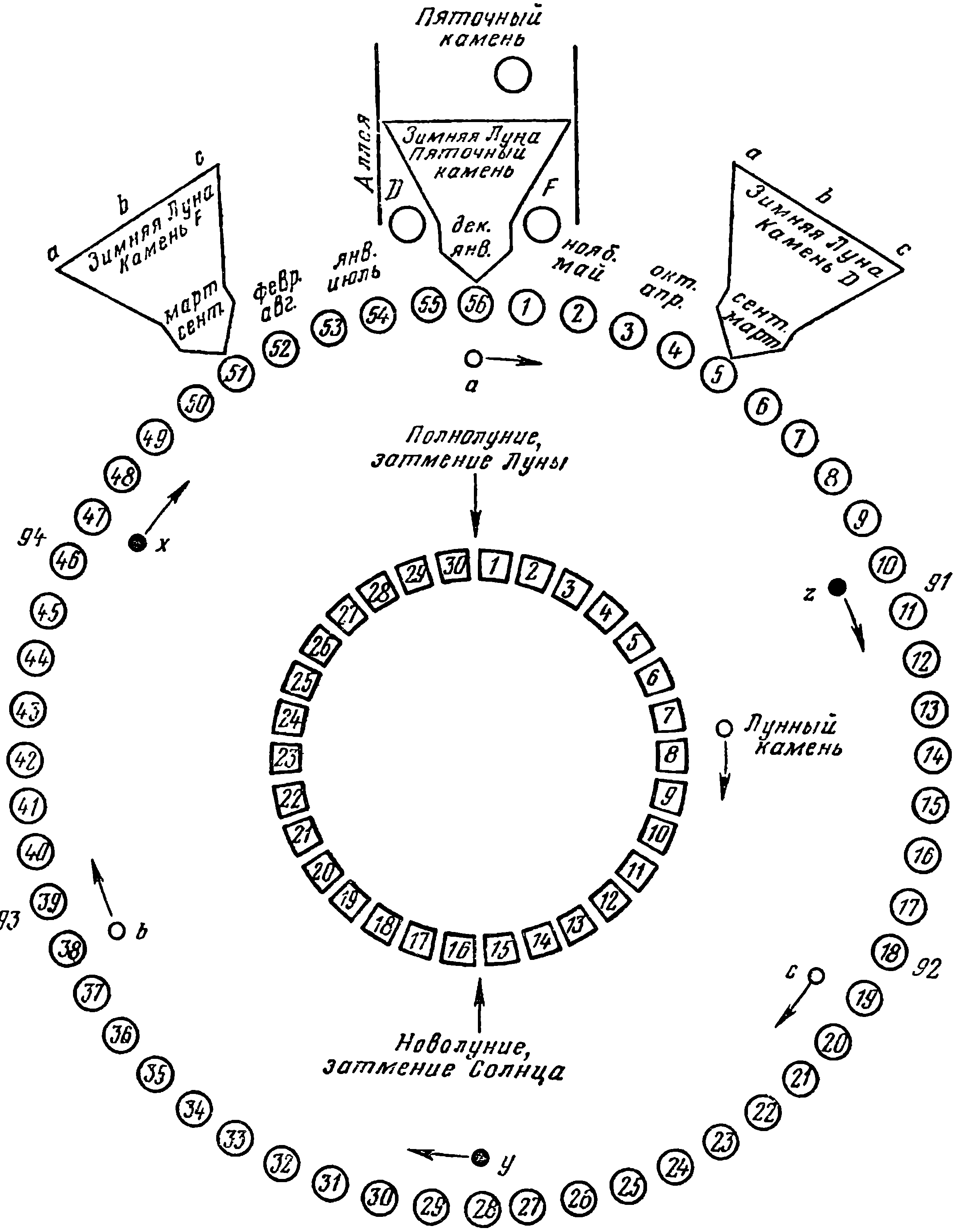
Частота восхода Луны в день зимнего солнцестояния над Пяточным камнем в два раза больше. Например, интервалы между годами 1694, 1685, 1676 и 1666 до н. э. составляют 9, 9 и 10 лет. За период с 2001 по 1000 г. до н. э. более редкий, десятилетний интервал составляет 33%. Однако если рассматривать двойной интервал (с 1694 по 1676 и с 1685 по 1666 г. до н. э.), то цикл опять чаще равен 19 годам, а 18-летний период повторяется с частотой, приведенной в табл. 1.

С такой же периодичностью Луна движется и относительно других направлений и ориентиров, в частности относительно линии 94—91 и трилитов. Даже восход Луны в направлении 92—93 в дни летних солнцестояний имеет ту же периодичность: 19, 19, 18. Солнце же возвращалось к тому же трилиту и Пяточному камню каждый год, в дни зимнего и летнего солнцестояний. Таким образом, 19-летний цикл был главным периодом, и этим, по-видимому, объясняется то возвращение небесных тел на прежние места, которое подразумевал Диодор. Но со временем жесткий 19-летний цикл нарушается и точка восхода Луны в день зимнего солнцестояния постепенно «уходит» от Пяточного камня; чтобы избежать этого, каждые 56 лет надо было вносить поправку.

С такой же периодичностью происходят солнечные и лунные затмения, и когда зимняя Луна восходит над Пяточным камнем, это означает, что должно произойти солнечное или лунное затмение. На рис. 1 указаны зимние затмения, происходившие в период с 1600 по 1400 г. до н. э. [4]. Следует отметить, что не более половины этих затмений могло наблюдаться из Стоунхенджа, и таким образом восход Луны над Пяточным камнем сигнализирует о наступлении «опасного» периода, когда затмения возможны [2].

Рис. 1. Азимуты восхода зимней Луны с 1600 по 1400 гг. до н. э. Ломаная линия — период по Стоунхенджу

В настоящее время я не могу с абсолютной уверенностью доказать, что Стоунхендж служил астрономической обсерваторией. Для этого понадобилась бы машина времени. Хотя линии, проходящие через пары камней, и совпадают с несколькими десятками направлений, указывающих на важные солнечные и лунные положения, строители Стоунхенджа все-таки могли и не знать об этом. Описание, данное Диодором, могло быть просто беспочвенной выдумкой. Но я, возможно, частично рассею сомнения, показав, каким образом астрономическая теория объясняет некоторые другие особенности Стоунхенджа.

Если взять двойные интервалы между годами, когда Луна восходит над маркировочными камнями, то четкой периодичности не выявляется: согласно табл. 1, Луна находится над камнями D и F каждые 37 или 38 лет. Однако следующий интервал для крайних значений азимутов удивительно постоянен — он почти всегда составляет 56 лет! Аналогично зимние восходы Луны над Пяточным камнем и затмения также происходят точно через 56 лет в 84% всех случаев (табл. 1). Это означает, что зимняя Луна возвращается в свое положение над каким-нибудь камнем каждые 56 лет, и многие такие циклы завершаются на протяжении одной человеческой жизни. Например, за 20-летний период наблюдений Луна займет 10 отмеченных мною положений [2] как относительно сарсенового кольца, так и относительно «опорных» камней. Каждое из этих событий является частью полного 56-летнего цикла и потому могло быть предсказано осведомленным человеком из рода, в котором эти сведения «передаются из поколения в поколение», как говорит Диодор.

Число 56 имеет большое значение для Стоунхенджа — это число лунок Обри, расположенных вдоль внешнего кольца. Если смотреть из центра, то угловые расстояния между этими лунками равны, то есть их азимуты распределены равномерно вдоль линии горизонта. Поэтому они не могут быть связаны ни с Солнцем, ни с Луной, ни с каким-либо другим небесным телом. Это подтверждается археологическими исследованиями: в лунках найдены следы костров и кремированные останки, но в них никогда не стояли камни. Если строители Стоунхенджа хотели просто разделить окружность на равные части, то почему они не вырыли 64 лунки, наметив их положения путем последовательного деления пополам дуги окружности на 2, 4, 8, 16, 32 и 64 части? Я считаю, что лунки Обри служили для отсчета лет (по одной лунке на каждый год) с целью предсказания положения Луны. Возможно, в течение года в одной из лунок производилась кремация тел или лунка отмечалась переносным камнем.

Рис. 2. Схематический план вычислительной машины «Стоунхендж»

Стоунхендж может быть использован в качестве цифровой вычислительной машины. Чтобы этот монумент каменного века заработал как вычислительная машина, сделайте следующее.

Возьмите три белых камешка a, b и c и положите их в лунки с номерами 56, 38 и 19, как показано на рис. 2. Затем возьмите три черных камешка x, y и z и положите их в лунки с номерами 47, 28 и 10. Каждый год, скажем, в день летнего или зимнего солнцестояния перекладывайте камешки по кругу в соседнюю лунку. Эта простая операция позволяет точно предсказывать все важные лунные события на протяжении многих сотен лет. Зададим, например, вопрос: «Когда полная Луна восходит над Пяточным камнем в день зимнего солнцестояния?» Ответ прост: «Когда в лунке 56 лежит камешек». (Лунка 56 — логичный ориентир, так как он расположен на линии центр—Пяточный камень.) В табл. 2 приведены критические годы, предсказанные по вычислительной машине «Стоунхендж» для периода с 1610 по 1450 г. до н. э., причем камни располагались так, что в 1610 г. камень (a) был в лунке 56. Этот период был выбран потому, что 1600 г. до н. э. — самый ранний год, для которого были вычислены затмения [4].

Таблица 2. Восходы зимней Луны над Пяточным камнем и затмения в периоды летнего и зимнего солнцестояний

Табл. 2 ясно показывает удивительную точность вычислительной машины «Стоунхендж». В 14 случаях из 18 год затмения был предсказан верно, а максимальная ошибка составляла одну единицу. Были предсказаны также годы, когда заход полной Луны, ближайший ко дню летнего солнцестояния, наблюдался через большой трилит (55—56). Кстати, в это время в лунке 28 находился камешек, лежащий на прямой большой трилит — центр.

Камешек, находящийся в лунке 56, предсказывает год, когда в интервале 15 дней до или после дня зимнего солнцестояния произойдет затмение Солнца или Луны; этот месяц называется периодом зимней Луны. Точно так же предсказываются затмения в середине лета в период летней Луны. В 1500 г. до н. э. день зимнего солнцестояния пришелся на 6 января (по юлианскому календарю), так что период в 30 дней (с 22 декабря 1501 г. до н. э. по 21 января 1500 г. до н. э.) был периодом зимней Луны. Аналогично период летней Луны и все времена года в 1500 г. до н. э. запаздывали на 15 дней по сравнению с датами григорианского календаря, которым мы пользуемся в настоящее время. В табл. 2 приведены фактические даты затмений; из них следует, что Стоунхендж как вычислительная машина предсказывал зимние и летние затмения со 100-процентной надежностью. Если в год происходило несколько затмений, то в табл. 2 приведено только одно. Чтобы читатель лучше представил себе, как работает эта вычислительная машина, поясним, что после 1610 г. до н. э. шесть перекладываемых камешков дают периоды 9, 9, 10, 9, 9, 10 и т. д. лет. Камешки a, b, c дают интервалы 18, 19, 19 и т. д. лет. Этот цикл соответствует лунному, так как равен 18,67 года, а период движения узлов лунной орбиты равен 18,61 года. Он соответствует циклу затмений, потому что метонов цикл (19 лет) и сарос (18 лет) представляют собой циклы затмений. Метонов цикл не был сразу распознан как цикл затмений — возможно, потому, что он справедлив только на протяжении 57 лет. Однако это весьма примечательный цикл, потому что затмения повторяются в одни и те же календарные дни. Например, за лунным затмением 19 декабря 1945 г. следует лунное затмение 19 декабря 1964 г.

Когда зимняя Луна восходит над камнем F и заходит в направлении 93—91? Когда летняя Луна восходит над точкой 91, если смотреть из точки 93? Когда равноденственная Луна восходит и заходит вдоль 94—C и когда происходят затмения в дни равноденствий? Ответ: когда в лунке 51 лежит белый камешек. В табл. 3 сравниваются предсказания и фактические данные. Точность опять вполне удовлетворительна.

Таблица 3. Восходы зимней Луны над камнем F и затмения Луны в периоды весеннего и осеннего равноденствий

Когда зимняя Луна восходит над камнем D и заходит в направлении 94—91? Когда летняя Луна восходит над насыпью 92, если смотреть из точки 93? Когда равноденственная Луна восходит и заходит вдоль 94—C и когда происходят затмения в дни равноденствий? Ответ на все эти вопросы таков: когда в лунке 5 лежит белый камешек. Результаты, приведенные в табл. 4, подтверждают точность вычислений на каменной машине.

Само собой разумеется, что табл. 2, 3 и 4 также предсказывают восходы и заходы Луны в амбразурах трилитов и арках сарсенового кольца, так как последние повторяют 10 лунно-солнечных направлений «опорных» камней.

В какие годы произойдет затмение в период между солнцестоянием и равноденствием? Для примера возьмите месяцы апрель и октябрь согласно нашему календарю. Ответ: затмения произойдут в те месяцы, когда в лунках 3 или 4 лежит какой-либо камешек.

На рис. 2 сектор между камнями 51 и 5 размечен таким образом, что по нему можно предсказывать периоды затмений согласно нашему календарю.

Таблица 4. Восходы зимней Луны над камнем D и затмения Луны в периоды весеннего и осеннего равноденствий

Оставалось только научиться предсказывать, какое из полнолуний является ближайшим ко дню солнцестояния или равноденствия. Средний интервал между двумя полнолуниями составляет 29,53 дня, и жрецы Стоунхенджа должны были как-то вести счет этим дням. Для этого достаточно было переносить камень поочередно в каждую из 30 арок сарсенового кольца. Если перемещать его каждый день на одну позицию, то полнолуния следовало ожидать, когда камень окажется в определенной арке, а именно в арке 30—1. Каждые два или три месяца надо было вносить поправки в положение камня на ±1 позицию из-за того, что лунный месяц содержит нецелое число суток. По мере приближения дня солнцестояния или равноденствия (что можно было установить по наблюдениям Солнца) жрец Стоунхенджа мог определить, которое из полнолуний будет к нему ближе всего. Сарсеновое кольцо могло также служить для уточнения дня затмения. Лунное затмение происходит, когда лунный камень лежит в арке 30—1, а солнечное, когда он находится в арке 15—16.

Полный анализ показывает, что в течение трех столетий эта каменная вычислительная машина работала точно, а затем явления, связанные с Луной, начали происходить на год раньше. Жрецы Стоунхенджа могли это легко заметить и исправить, переложив шесть камней на одну лунку вперед. В наши дни эта операция называется подстройкой и используется во всех современных вычислительных машинах и логических схемах. Инструкцию по эксплуатации вычислительной машины «Стоунхендж» достаточно было дополнить одним простым правилом: если лунные события наступают на год раньше, чем следует из положения какого-либо камня (например, камня a), передвиньте все шесть камней на одну лунку вперед. Это довольно простая поправка. Если ошибка не была замечена с камнем (a) (скажем, из-за облачной погоды), ее можно исправить со следующими камнями: x, b, y и т. д. Поправку необходимо производить примерно каждые 300 лет, например в 2001, 1778 и 1443 гг. до н. э.

Прецессия земной оси не влияет на точность работы машины, а изменения угла наклона эклиптики и лунной орбиты также несущественны. Например, в текущем 1964 г. камень (a) находится в лунке 56. Полная Луна взойдет над Пяточным камнем 19 декабря, ее затмение произойдет в 2 часа 35 минут по полуночи и она зайдет в направлении 94—G. Следующее зимнее затмение будет также видно из Стоунхенджа; оно произойдет через 9 лет, 10 декабря 1973 г., когда в лунке 56 будет находиться камень (x). Вычислительная машина «Стоунхендж» будет работать и после 2100 г., а затем потребуется подстройка на одну позицию; затем машина будет работать еще по крайней мере 300 лет, прежде чем понадобится дальнейшая подстройка.

Литература

1. Diodorus of Sicily, Book II, 47, Harvard Univ. Press, Cambridge, 1935.

2. Hawkins G.S., Nature, 200, 306 (1963).

3. Explanatory Supplement to the Astronomical Ephemeris, H.M.S.O., London, 1961.

4. Van den Bergh G., Eclipses — 1600 to —1207, Tjeenk, Willink and Zoon, Holland, 1954.

5. Newham C.A., The Enigma of Stonehenge, частное сообщение, 1964.

Примечания

1. Эта статья была опубликована в журнале Nature от 27 июня 1964 г.