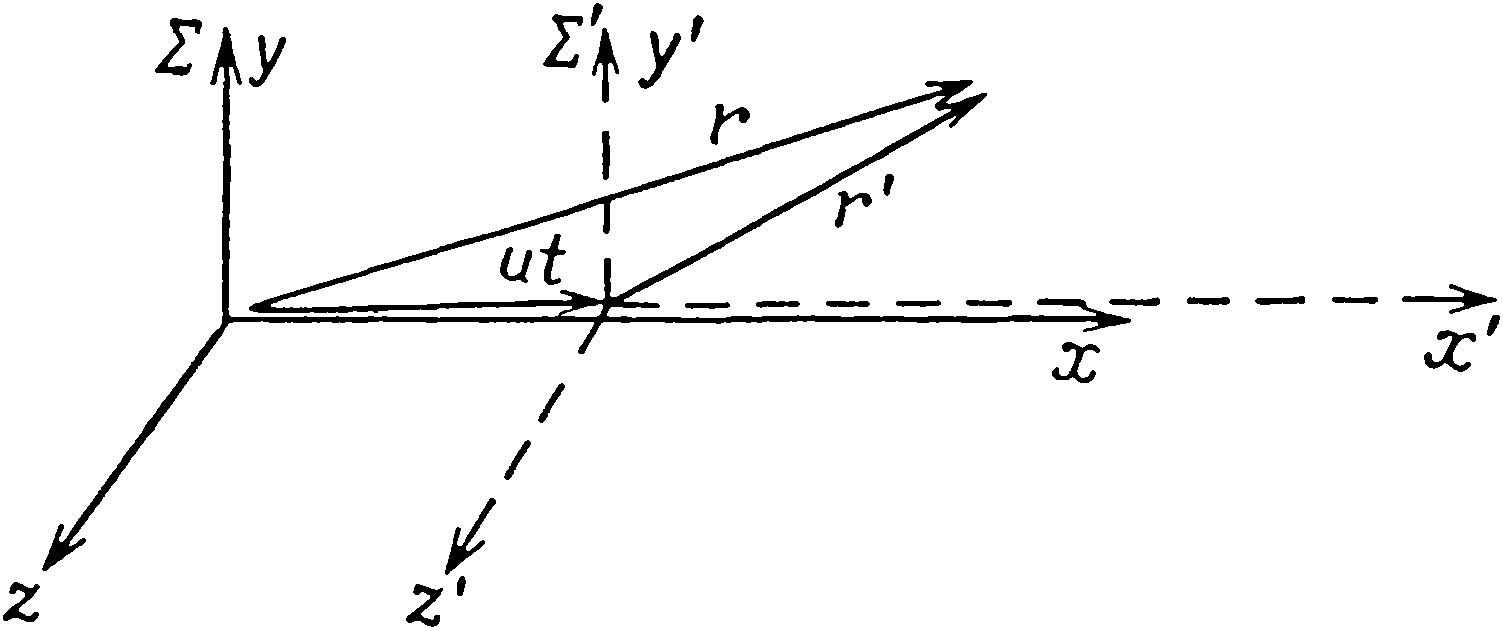
Взгляд на ньютоновскую и эйнштейновскую физику

Читая Discorsi, глубоко проникаешься удивлением, сколь обширен вклад Галилея в науку, сделанный им в глубокой старости и несмотря на перенесенное им осуждение со всеми его последствиями. В корне ложен образ Галилея, когда представляют, будто после своего отречения он преисполнился покорности или даже занимался самообвинениями как изменивший делу науки. Если учесть все обстоятельства, действовавшие в тогдашнем обществе и в полной мере влиявшие также на Галилея, то можно единственно утверждать, что Галилей знал, на что он идет. Его жизнь была жизнью создавшего целую эпоху исследователя и вместе с тем жизнью борца против догматической псевдонауки, и эта жизнь была преисполнена последовательности в проведении его научной линии:

Даже слепота не парализовала постоянной активности Галилея. Свое письмо самому верному другу Миканцио от 30 января 1638 г. он заканчивал словами:

«Так что я не прекращаю даже в охватившей меня темноте строить рассуждения по поводу то одного, то другого явления природы, и я не смог бы дать своему беспокойному уму отдыха, даже если бы пожелал того. Такое возбуждение мне очень вредит, ибо оно принуждает меня постоянно бодрствовать».

Галилей как сын своего времени субъективно в определенном смысле более тяготел к феодализму, чем к буржуазному обществу, что проявилось и при его переезде из Венецианской республики во Флоренцию, ко двору великого герцога. Однако несомненно, что объективно он сыграл роль сияющего маяка в общественной жизни. Как подчеркивает Кузнецов [C 5], «инквизиция осудила Галилея, так как наука в его руках стала мощной общественной силой, направленной против пережитков в общественных отношениях».

Рассматривая как Dialogo, так и Discorsi, мы снова и снова обнаруживали, что ставившаяся Галилеем проблематика в идейном отношении непосредственно ведет к ньютоновской и эйнштейновской физике. Поэтому не хотелось бы завершать это изложение, хотя бы просто не указав на те фундаментальные вопросы физики, с которыми имеется такая взаимосвязь [C 12].

Известно, что впервые к количественной формулировке законов механики подойти смог только Ньютон, когда он создал аппарат математического анализа, отвечавший потребностям физики. Его Philosophiae Naturalis Principia Mathematica («Математические начала натуральной философии») создали основу для целой ньютоновской эпохи в физике. В этом труде ему удалось собрать квинтэссенцию всех фундаментальных физических знаний того времени. Он исходил из принципиальных основ физического исследования и начал с того, что сформулировал представления об основных для физики понятиях пространства и времени, в которых он усматривал абсолютные категории. Итак, он определил:

«Абсолютное пространство по самой своей сущности, безотносительно к чему-либо внешнему, остается всегда одинаковым и неподвижным.

Абсолютное, истинное, математическое время само по себе и по своей сущности, без всякого отношения к чему-либо внешнему, протекает равномерно...»

Основываясь на этих понятиях пространства и времени, Ньютон, который не желал «измышлять гипотез», построил свою физику. Лишь Эйнштейну удалось почти 250 лет спустя обнаружить, что эти представления о пространстве и времени являются неприемлемыми гипотезами.

Содержание ньютоновской физики состоит из трех аксиом механики Ньютона:

1. Закон инерции. Каждое тело, когда на него не действуют никакие силы, сохраняет состояние покоя или равномерного прямолинейного движения. (О физическом авторстве Галилея в формулировке этого закона мы уже подробно говорили).

2. Закон движения. Движение тела подчиняется закону

dp/dt = m_Tb = K,

где p = m_Tdr/dt.

(Здесь p — импульс, r — радиус-вектор тела, dr/dt — вектор скорости, b = d²r/dr — ускорение, m_T— инертная масса и K — сила.)

3. Закон действия и противодействия. Действию всегда есть равное и противоположное противодействие.

Кроме того, сюда входит еще закон всемирного тяготения Ньютона:

G = −γ (m_sM_s/r³)r.

(Здесь G — сила тяготения, γ — ньютоновская гравитационная постоянная, m_s и M_s — тяготеющие массы, r — радиус-вектор между двумя телами, r — абсолютное значение r.) Этот закон описывает силу тяготения, действующую между притягивающими друг друга тяготеющими массами.

Рассмотрим тело, обладающее инертной массой m_T и тяготеющей массой m_s, на которое действует сила тяготения со стороны одной отдельно взятой тяготеющей массы M_s. Тогда K= G, и уравнение движения принимает вид

m_Tb = −γ (m_sM_s/r³)r,

иначе

b = −γ (m_s/m_T M_s/r³)r,

Если учесть в этом уравнении вывод, принадлежащий главным образом Галилею, что ускорение тела при падении не зависит от массы этого тела, то мы придем к утверждению, что

m_s/m_T есть мировая постоянная,

так как в величину b не может входить никакая величина, характеризующая данное тело. Если включить эту мировую постоянную в состав ньютоновской гравитационной постоянной, мы будем иметь без нарушения общности

m_s = m_T.

Итак, мы вывели фундаментальный факт равенства инертной и тяготеющей масс.

Уже в ньютоновской физике исследователи обратили внимание на два принципиально разных типа систем отсчета, причем под системой отсчета следует понимать совокупность материальных объектов, к которым физики относят свои измерения:

Рис 8. Две инерциальные системы отсчета, движущиеся относительно друг друга

1. Инерциальные системы, которые находятся в состоянии покоя или равномерного движения относительно системы неподвижных звезд.

2. Неинерциальные системы, находящиеся относительно системы неподвижных звезд в состоянии ускоренного движения (такова, например, вращающаяся карусель).

Рассмотрим теперь две инерциальные системы отсчета Σ и Σ′, движущиеся друг относительно друга со скоростью и, по необходимости постоянной. Тогда соответственно пространственные и временная координаты этих инерциальных систем будут связаны между собой преобразованием Галилея

r′ = r − ut,
t′ = t,

названным так в честь первооткрывателя представления об относительности (рис. 8). В согласии с представлениями Ньютона об абсолютности времени в обеих системах отсчета время одно и то же.

Далее перед физиком-теоретиком стоит вопрос, меняет ли свой вид или сохраняет его ньютоновский закон движения как фундаментальный закон природы, когда с помощью преобразования Галилея совершается переход от одной инерциальной системы отсчета к другой. Дифференцирование уравнений этого преобразования дает

dr′/dt′ = dr/dt − u, d²r′/dt′² = d²r/dt².

Поэтому от закона движения в инерциальной системе Σ

m_T (d²r/dt²) = K

мы приходим в системе Σ′ к закону

m_T (d²r′/dt′²) = K.

Тем самым установлено, что ньютоновский закон движения форм-инвариантен (ковариантен) относительно преобразований Галилея. Этот факт констатируется в названном также в честь Галилея принципе относительности Галилея:

«В двух движущихся друг относительно друга инерциальных системах отсчета, связанных между собой преобразованием Галилея, ньютоновский закон движения имеет один и тот же вид».

Значит, никакая инерциальная система ничем не выделяется из других инерциальных систем. В уравнения движения не входит скорость относительно какой-либо инерциальной системы отсчета, которую можно было бы рассматривать как абсолютно покоящуюся относительно пространства и тем самым привилегированную.

В этом состоит самая характерная черта ньютоновской физики, достигшей огромных успехов за более чем двести лет своего существования как в земных, так и в космических приложениях.

К концу XIX столетия техника эксперимента в области электромагнитных явлений, и особенно в оптике, достигла такого высокого уровня развития, что физики были поставлены перед лицом удивительного факта, вытекавшего из результатов знаменитого опыта Майкельсона и анализа распространения света от двойных звезд, с определенностью указывавших на постоянство скорости света. Этот факт состоял в том, что уравнения Максвелла — основные уравнения при описании всех электромагнитных явлений — оказались не форм-инвариантными относительно преобразований Галилея в противоположность уравнениям движения ньютоновской механики, инвариантность которых была установлена выше.

В результате попыток устранить это противоречие между механикой и электродинамикой в 1905 г. Альбертом Эйнштейном была создана специальная теория относительности; его предшественниками были Фойгт, Лоренц, Пуанкаре, Хазенэрль и др., которые, однако, по большей части не смогли освободиться от господствовавшей тогда концепции мирового эфира.

Непреходящей заслугой гения Эйнштейна было то, что он, исходя из глубоко философских соображений, поставил во главу угла принцип единства физики и добился согласия между механикой и теорией электромагнетизма. Он произвел последовательное обобщение принципа относительности Галилея и пришел к специальному принципу относительности Эйнштейна:

«В двух движущихся относительно друг друга инерциальных системах отсчета законы природы имеют один и тот же вид».

Если сравнить эту формулировку с выражением принципа относительности Галилея, обнаруживается то существенное различие, что принцип относительности Галилея относится только к механике, тогда как эйнштейновский принцип охватывает всю физику (исключая лишь гравитацию).

Зададимся вопросом, какие эпистемологические предположения должен был привлечь Эйнштейн для того, чтобы непротиворечиво реализовать свой принцип относительности. Об этом и пойдет теперь речь.

Эйнштейн подверг основательной критике ньютоновские концепции абсолютного пространства и абсолютного времени и пришел к выводу, что сами по себе пространство и время суть относительные категории, собственно же предметом и основой физического исследования является четырехмерный пространственно-временной континуум. Тем самым был сделан переход от 3-мерного к 4-мерному мышлению. Пассивной ареной, на которой протекают физические явления, стало пространство-время. При этом его геометрия постулировалась как псевдоевклидова, т. е. плоская, и пространство-время рассматривалось как предельно лишенное структуры и бесконечно протяженное. Пока что принципиально новым моментом по сравнению с ньютоновским пространством был переход от трехмерности к четырехмерности. В теории Ньютона абсолютное время играло роль абсолютного стандарта для всего мира, что находило свое отражение в уравнениях физики в том, что время было самостоятельным параметром. Напротив, эйнштейновская релятивизация времени и его объединение с пространством привели к равноправию пространства и времени. В дальнейшем оба понятия должны были фигурировать в законах природы симметричным образом.

Эта фундаментальная идея должна была математически выражаться в том, что каждой системе отсчета следовало приписать свое собственное относительное время. Тем самым был получен ответ и на вопрос о противоречии, возникшем в результате опыта Майкельсона.

В своей знаменитой работе 1905 года «К электродинамике движущихся тел» Эйнштейну удалось вывести названные им в честь Лоренца преобразования:

x′ = (x − ut)/ √(1 − (u/c)²), y′ = y, z′ = z,

t′= (t − ux/c²)/ √(1 − (u/c)²),

которые описывают переход от одной инерциальной системы отсчета к другой.

Когда относительная скорость систем отсчета мала,

(uc)² ≪ 1,

преобразования Лоренца принимают вид

x′ = x − ut, y′ = y, z′ = z, t′=t,

а это и есть преобразования Галилея, записанные через свои компоненты. Тем самым была обеспечена необходимая преемственность между физикой Эйнштейна и физикой Ньютона, причем в случае больших скоростей и высоких энергий последняя вырождается в слишком грубое приближение действительности.

Этот схематический набросок специальной теории относительности приводит нас и к кругу основных идей общей теории относительности [C 12]. Специальный принцип относительности Эйнштейна, подобно принципу относительности Галилея, ограничивается использованием инерциальных систем отсчета, т. е. систем, находящихся в состоянии равномерного движения. В течение почти 10 лет Эйнштейн работал над тем, чтобы снять это ограничение. В результате в 1915 г. ему удалось создать свою общую теорию относительности, справедливую при любых типах движения систем отсчета. Ее сущность формулируется в общем принципе относительности Эйнштейна:

«Законы природы имеют один и тот же вид в произвольных системах отсчета¹.»

Так Эйнштейн освободился от понятия инерциальной системы отсчета.

Математическим аппаратом, позволяющим конкретно выразить эту всеобъемлющую теорию, является тензорное и спинорное исчисление.

Применение общего принципа относительности к механике и теории электромагнетизма не принесло Эйнштейну особых неожиданностей. Однако обобщение ньютоновской теории тяготения привело к открытию совершенно новых фактов о структуре пространства и времени.

Эйнштейн пришел индуктивным путем к заключению, что реальное пространство-время может быть не псевдоевклидовым, т. е. плоским, но искривленным в соответствии с законами римановой геометрии. Он исходил из тех соображений, что пассивная роль пространства-времени в специальной теории относительности не может давать полного выражения сущности пространства-времени как атрибута материи, но что структура пространства-времени должна быть сама следствием состояния движения материи, и обратно, состояние движения материи должно обусловливаться структурой пространства-времени. Эту обоюдную взаимосвязь он сумел математически выразить в своих знаменитых уравнениях гравитационного поля.

Для слабо искривленного пространства-времени, существующего в наших земных условиях, уравнения поля Эйнштейна переходит в указанное выше уравнение поля Ньютона. Тем самым преемственность сменяющих друг друга физических теорий обеспечивается и в этой области.

Теория относительности лежит в основе всех разделов физики, так как их основные постулаты должны быть в конечном счете согласованы между собой. Большой успех был достигнут и в квантовой теории, когда Дирак сумел дать ее релятивистскую формулировку.

Особой областью приложения эйнштейновской теории является релятивистская космология, из которой мы черпаем сведения о структуре Вселенной как целого.

Бросая сегодня ретроспективный взгляд на физику, мы видим, что современность связывает с эпохой Средних веков цепь идей, в которой сверкают поистине бриллианты. Благодаря гению Галилея, Ньютона, Эйнштейна и многих других наука стала плодом цивилизации, находящимся на службе всего человечества.

Примечания

1. Вообще говоря, так называемый общий принцип относительности (или строго локальный принцип эквивалентности гравитационных и инерционных сил) послужил лишь эффективным эвристическим средством для построения общей теории относительности Эйнштейна. — Прим. ред.