7. Планетные системы до Коперника

Мы рассмотрели, какими путями Коперник подходил к своему открытию, теперь следует остановиться на том, как человечество в своем развитии представлений о планетной системе подошло к исходным позициям Коперника, иными словами, окинуть взором историю планетной астрономии от древнейших времен до построения коперниканской теории.

Употребляемые сейчас названия планет — имена богов древних римлян — это латинские переводы их греческих имен: Меркурий — греч. Гермес, Венера — Афродита, Марс — Арес, Юпитер — Зевс, Сатурн — Крон. Эти греческие имена богов были «присвоены» планетам примерно в середине IV в. до н. э. — об этом свидетельствует, в частности, тот факт, что древнегреческий философ Аристотель, живший с 384 по 322 г. до н. э., употреблял уже эти новые, «божественные», имена планет, тогда как его учитель Платон (427—347 г. до н. э.) пользовался еще старыми, пифагорейскими их названиями. Так как эти пифагорейские названия планет были известны Копернику, приведем их здесь: это Стильбон (Меркурий), Фосфор и Геспер (Венера утром и вечером), Пироент (Марс), Фаэтон (Юпитер) и Файнон (Сатурн). В свою очередь греческие названия были переводами с вавилонского: Гермес — вавилонское Набу — бог-покровитель Борсиппы, предместья Вавилона, бог письменности и торговли; Афродита — Иштар — богиня плодородия и любви; Арес — Нергал — бог войны и чумы; Зевс — Мардук — бог-покровитель Вавилона; Крон — Нину рта — бог осеннего Солнца и бог-покровитель Ниппура, древней шумерской столицы.

Но и эти названия не были новыми. За исключением Иштар, «божественность» которой признавалась еще в III тысячелетии до н. э. (она вместе с богом Луны — Сином и богом Солнца — Шамашем составляла божественную троицу), вавилонские «божественные» имена планет стали употребляться примерно в VII—VI вв. до н. э., в эпоху нововавилонского царства, когда самая яркая после Венеры-Иштар планета Юпитер получила имя Мардука — бога-покровителя столицы этого государства. Присвоение планетам имен богов именно в то время легко объясняется: когда многочисленные боги больших и малых государств не смогли защитить своих подопечных от разраставшейся Персидской империи, роль их пришлось ограничить объявлением велений рока, поместив их для этого на планеты, расположение которых на небосводе и должно было определять судьбы целых народов и отдельных людей. Как раз к этому времени относится широкое распространение астрологии.

Система гомоцентрических сфер Евдокса для Солнца и неподвижных звезд. а — неподвижная сфера, связанная с неподвижной Землей; б — подвижная сфера, на которой расположены все звезды. Экватор этой сферы скользит по экватору неподвижной сферы, совершая один оборот в сутки. На сфере неподвижных звезд — линия эклиптики, ось которой вращается вместе с этой сферой, описывая на ней северный и южный полярные круги; в — сфера, экватор которой скользит по эклиптике, совершая один оборот в год. Ее полюса совпадают с полюсами эклиптики. На экваторе этой сферы находится Солнце, которое проходит каждый знак зодиака за 1/12 часть года. Полгода оно выше экватора, а полгода ниже его, чем объясняется смена времен года. Прямая, на которой пересекаются плоскости экватора и эклиптики, неподвижна на сфере и называется линией равноденствия

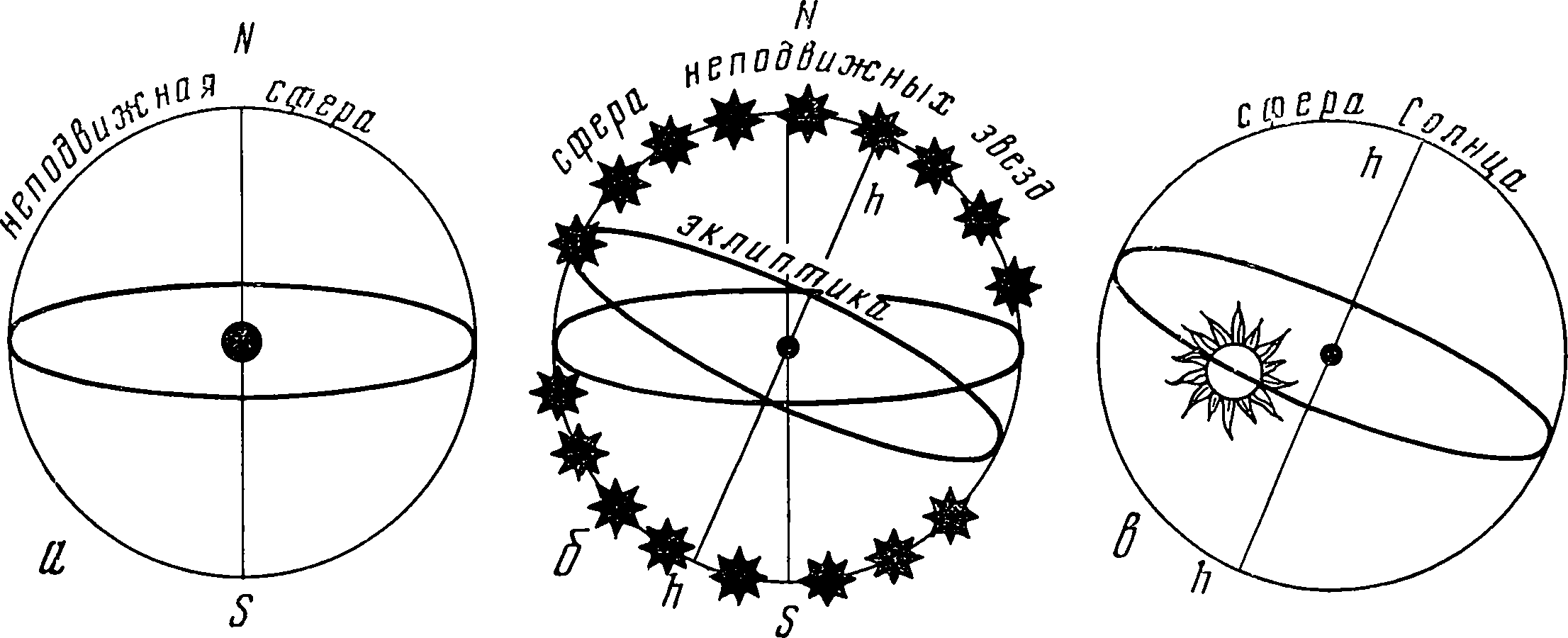
К этому времени уже была точно определена продолжительность тропического года и лунных месяцев, что позволило правильно отрегулировать лунно-солнечный год (19-летний цикл), который до сих пор сохранился в еврейском, а также в христианском («пасхальном») календаре; были выработаны математические методы, необходимые для предвычисления будущих астрономических событий, — таким образом было установлено одно из существенных положений современной науки, а именно, что естественные процессы могут быть выражены при помощи математических формул.

Несовершенство вавилонской астрономии заключалось в том, что она, умея достаточно точно предсказывать наступление отдельных астрономических событий, не ставила вопроса об их физической сущности, не рассматривала всего процесса непрерывного движения планеты — иными словами, ее интересовала только математика, но не механика планетных движений.

Вопрос о механике движений планет был поставлен греческими астрономами. Они стремились найти механизм, с помощью которого можно было бы воспроизвести все движение данной планеты, рассматриваемой как некая материальная точка. Так как все объекты надлунного мира считались совершенными, неизменными и вечными, предполагалось, что и их естественное движение должно быть тоже неизменным и вечным, т. е. круговым и равномерным. Поэтому Платон поставил перед своими учениками задачу — представить движение планет как комбинацию равномерных круговых движений или вращений (в то время, как мы знаем, круговое движение точки еще не умели отличать от вращения). Эта задача была решена младшим современником Платона Евдоксом Книдским (приблизительно около 360 г. до н. э.). Все движения планет он получал сложением равномерных вращений ряда сфер, на поверхности которых находились планеты; центры этих сфер совпадали с центром Земли (так называемые гомоцентрические сферы). Суточное движение неподвижных звезд представлялось в виде вращения сферы, которое совершалось с периодом в одни сутки вокруг оси, проходящей через полюсы Земли. На поверхности этой сферы выделялся большой круг — траектория годового движения Солнца (эклиптика). Чтобы описать движение Солнца по эклиптике, надо было поместить его на экваторе еще одной сферы, которая вращалась бы вокруг оси, проходящей через полюсы эклиптики. Совокупность двух этих вращений и представляла видимое движение Солнца по небесному своду в течение года.

Примерно таким же образом определялось движение Луны. Осложнение заключалось лишь в том, что ее орбита не совпадала с эклиптикой и, кроме того, точки ее пересечения с эклиптикой перемещались по эклиптике с периодом примерно в 19 лет. Это требовало введения уже трех сфер, которые вращались с периодами соответственно в одни сутки, в один год и в 19 лет, и еще одной сферы, на экваторе которой помещалась Луна. Эта сфера, вращаясь вокруг полюсов лунной орбиты с периодом в один лунный месяц, заставляла Луну перемещаться по ее орбите тоже за один месяц. У остальных планет движение рассматривалось только по долготе, поэтому эклиптику можно было считать орбитой планеты. Зная сидерический (звездный) период движения планеты, можно было представить ее среднее движение по эклиптике также в виде сложения движений трех сфер: одной — для суточного движения, другой — для годового и третьей — для движения по эклиптике планеты с периодом, равным времени сидерического движения. Чтобы получить истинное движение планеты, надо было добавить перемещение планеты относительно ее среднего положения — это перемещение можно было рассматривать как гармоническое колебание с центром в среднем положении. Поскольку такое перемещение получалось вследствие того, что планета наблюдалась с движущейся Земли, период этого колебания можно было принять равным одному году, а амплитуду — равной наибольшему отклонению планеты от своего среднего положения.

Полное лунное затмение по Аристарху Самосскому. Вершина M конуса тени, отбрасываемой Землей, лежит вне отрезка, соединяющего центры. Солнца и Земли. Отрезок ON определяет границы тени Земли на уровне Луны. Видно, что Солнце больше Земли

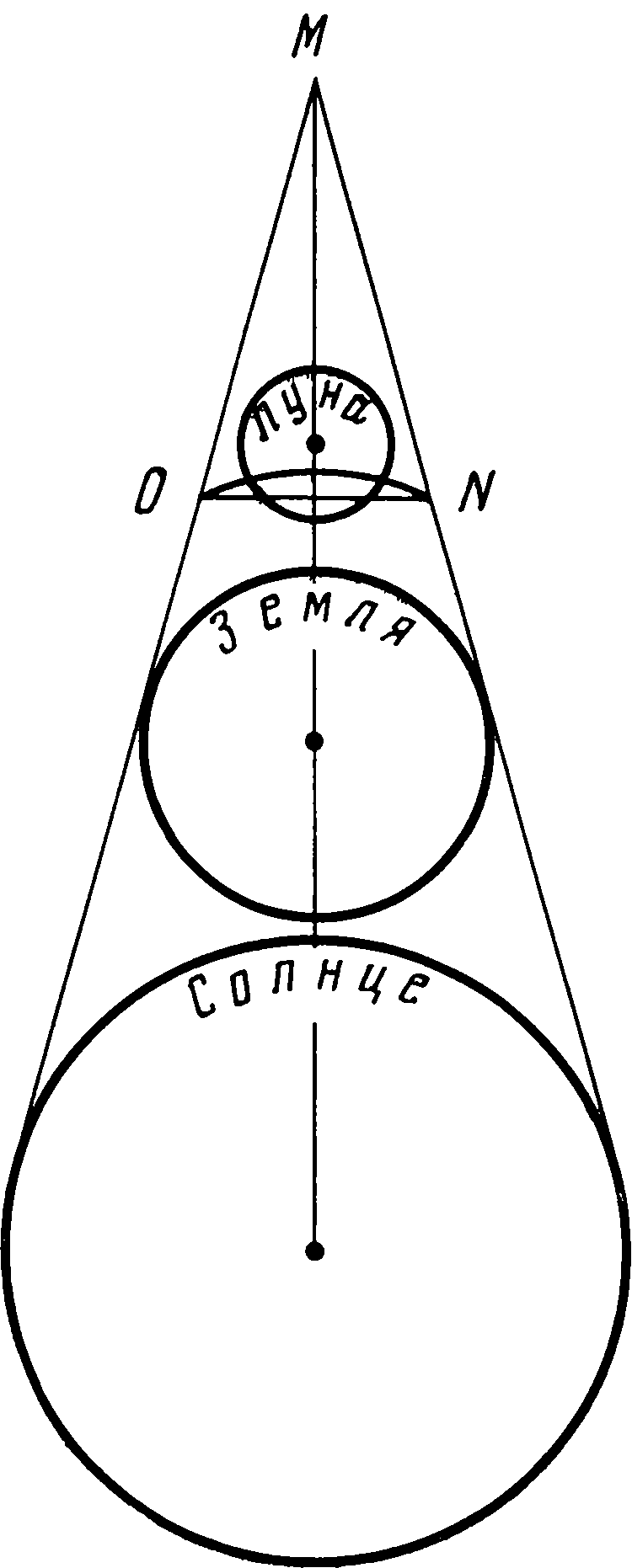
Построения Евдокса были проверены его учеником Каллипом, и полученные результаты одобрены самим Аристотелем. Это обстоятельство привело к тому, что теория гомоцентрических сфер была принята арабскими философами, в частности Ибн-Рушдом (Аверроэсом), а после них и средневековыми схоластиками. Она нашла последователя даже во времена Коперника — это был уже упоминавшийся нами итальянец Джироламо Фракасторо.

Однако система Евдокса имела и существенные недостатки. Так как каждая планета двигалась по сфере, центром которой являлась Земля, то во все время движения, находясь на одинаковом расстоянии от Земли, планета должна была сохранять одинаковую яркость. Но это в действительности не имело места для самой яркой планеты — Венеры, на что обратил внимание ученик Платона Гераклид Понтийский (ок. 300 г. до н. э.). Учитывая, что Венера не может удаляться от Солнца более чем на 45°, Гераклид предположил, что она должна вращаться вокруг Солнца; таким образом, ее расстояние от Земли меняется, а это отражается и на ее яркости. То же самое имело место и для Меркурия. Мнение, что обе эти планеты вращаются вокруг Солнца, сохранялось до конца Римской империи.

Третьей «непослушной» планетой оказался Марс, который, находясь в противостоянии с Солнцем, имел гораздо большую яркость, чем в соединениях. Так как эти противостояния и соединения могли происходить в любых местах зодиака, это означало, что орбита Марса должна охватывать не только Землю, но и Солнце. Этому можно было дать двоякое объяснение: или Марс должен вращаться вокруг Солнца, а Солнце вокруг Земли, или же Земля, находясь между Солнцем и Марсом, должна вращаться вокруг Солнца.

Такое заключение было очевидным для другого великого астронома античности — Аристарха Самосского, жившего в первой половине III в. до н. э. Наблюдая время прохождения Луны через тень Земли в течение лунного затмения, он установил, что у конуса тени, которую Земля отбрасывает от Солнца, вершина лежит вне отрезка, соединяющего центры Земли и Солнца. Поскольку этот конус представляет собой общую обертывающую для сфер Земли и Солнца, диаметр Солнца должен быть больше диаметра Земли примерно в отношении 19 к 3, а расстояние от Земли до Солнца примерно в 20 раз больше расстояния от Земли до Луны. Это в свою очередь приводит к выводу, что объем Солнца должен быть примерно в (19/3)³ раз больше объема Земли, а если так, то гораздо более вероятно, что Земля должна вращаться вокруг большего тела — Солнца, а не наоборот. Так родилась первая гелиоцентрическая модель строения Солнечной системы.

Почему же в дальнейшем развитии астрономии она не удержалась? Дело в том, что модель Аристарха основана на несовместимых предположениях: 1) все небесные светила должны вращаться вокруг некоторого центрального тела; 2) все движения планет вокруг этого тела должны быть равномерными.

Клавдий Птолемей. Старинная гравюра

Однако уже предшественники Аристарха, афинские астрономы Метон и Евктемон (середина V в. до н. э.), знали, что продолжительность астрономических времен года (от равноденствия до солнцестояния и обратно) неодинакова. От весеннего равноденствия до летнего солнцестояния проходит 93 дня, от этого солнцестояния до осеннего равноденствия — 90 дней, столько же от осеннего равноденствия до зимнего солнцестояния, а от зимнего солнцестояния до весеннего равноденствия 93 дня. В V в. до н. э. этими отклонениями можно было пренебрегать, считая их лежащими в пределах ошибки наблюдений, но когда стали известны более точные вавилонские наблюдения (это было около 200 г. до н. э.), стало ясно, что эти отклонения действительно существуют, и второе основное положение Аристарха о равномерном движении планет оказалось неверным.

Но равномерность круговых движений небесных тел считалась основным законом их естественных движений, причем так думали и во времена Копер-ника. Чтобы спасти эту аксиому, Гиппарх около 150 г. до н. э. предположил, что эта неравномерность является только кажущейся и происходит оттого, что мы наблюдаем движения светил не из центра их орбит, а из какой-то другой точки, иными словами, что центр Земли не является центром вращений планет. Таким образом, Гиппарх пожертвовал первой аксиомой Аристарха Самосского, заставив планеты вращаться не вокруг материального тела (Земли), а вокруг некоторой геометрической точки, положение которой он и определил. Соответствующая орбита светила получила название эксцентра.

Система мира по Птолемею

Любопытно, что через 1800 лет после Гиппарха Кеплер пришел к диаметрально противоположному решению: он заставил планеты вращаться вокруг материального тела (Солнца), но не по окружностям, а по эллипсам, и вдобавок с изменяющейся скоростью.

Итак, Гиппарх разработал теорию видимого движения Солнца вокруг Земли по эксцентру. Теория движения планет была получена через 300 лет после него (александрийским астрономом Клавдием Птолемеем около 150 г. н. э.). Но культурная атмосфера в это время была уже другой. В предшествующую эпоху астрология уже существовала (она была основой философской системы стоиков), но в чистую науку еще не вторгалась; была сильна материалистическая школа эпикурейцев, продолжали работать последователи Аристотеля и Платона. Уже была создана тригонометрия, как плоская, так и сферическая, улучшены вавилонские методы расчета планетных движений, начинала формироваться алгебраическая математика, достигшая расцвета позже, в деятельности Диофанта, в III в. н. э. Теперь же, когда начался упадок Римской империи, мистика и астрология стали господствовать повсюду. Не уберегся от нее и Птолемей, астрологические труды которого пользовались большой известностью. Следы астрологии (правда, только следы) внимательный читатель может найти даже в его знаменитом произведении «Альмагест». Наиболее заметно это сказалось в том, что у Птолемея Земля — центр, вокруг которого должны вращаться все планеты, в том числе и Венера с Меркурием.

Объяснение видимых попятных и петлеобразных движений планет по Птолемею. Планета П движется по эпициклу, центр которого перемещается но эксцентрической окружности с центром в Ц (Земля находится в эксцентре З). Образующаяся при сложении этих движений траектория выделена жирной линией

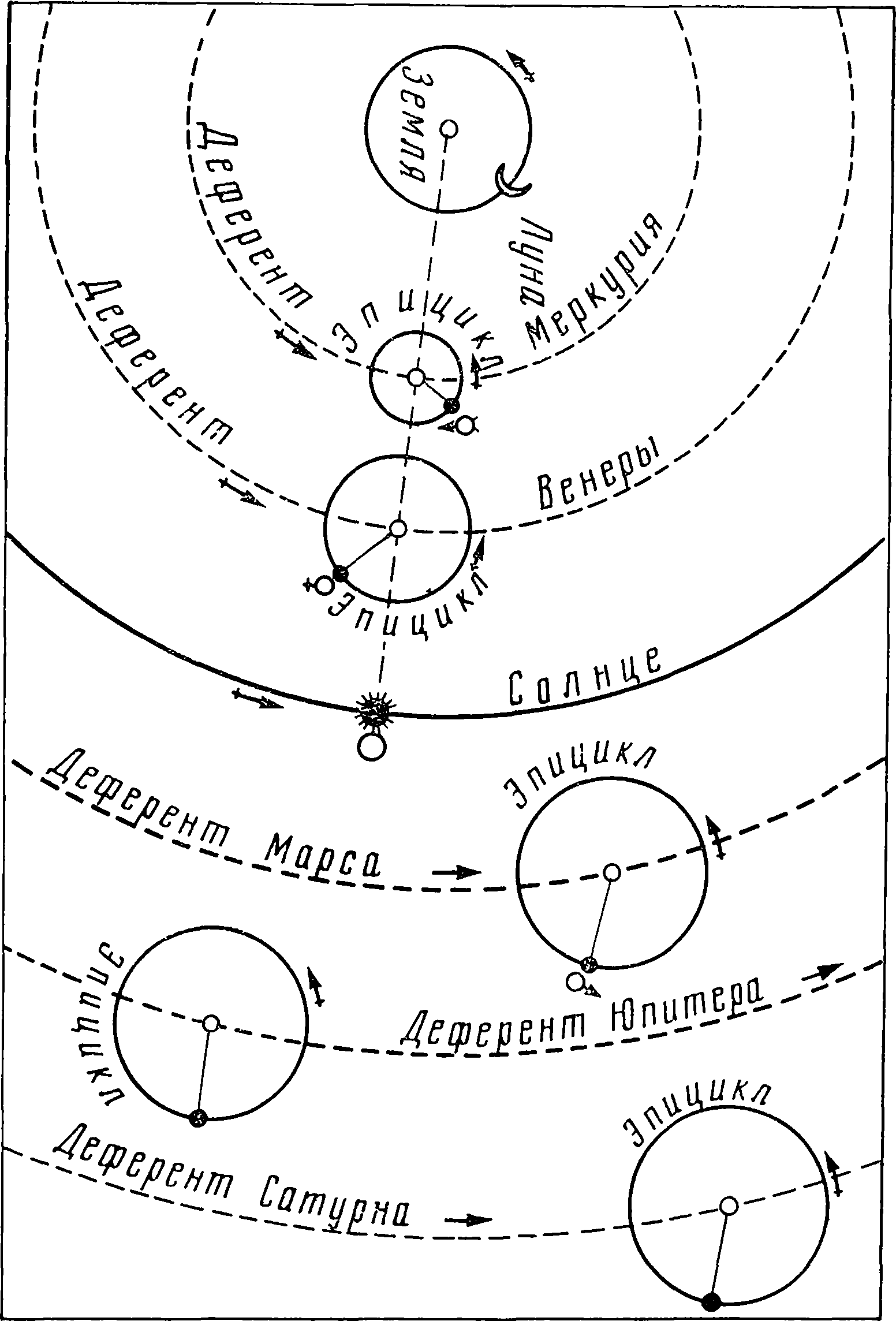
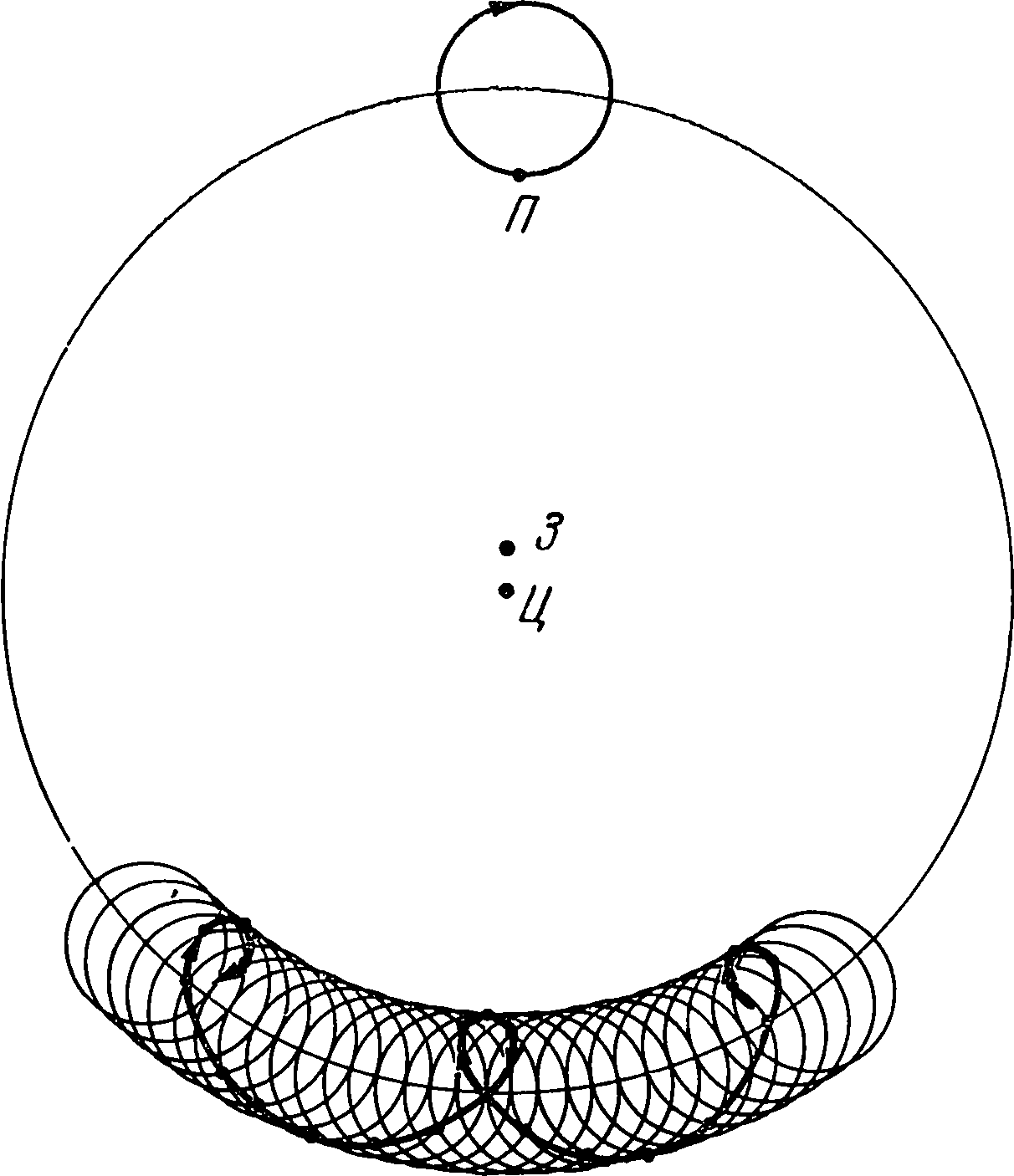
Схема Птолемеевых расчетов движения планет заключалась в следующем. Птолемей исходил из некоторого среднего равномерного движения планеты, к которому прибавлялись поправки, так называемые неравенства. Основных поправок было две. Одна из них вызывалась тем, что в действительности планета движется по эллипсу, поэтому в различных местах орбиты меняется ее скорость. Эта поправка называлась неравенством в отношении зодиака и исправлялась путем введения эксцентра (или деферента). Другая поправка появлялась вследствие того, что наблюдения велись с движущейся Земли, поэтому планета совершала то прямое движение (против часовой стрелки), то обратное, а в некоторых точках останавливалась — получалось так называемое стояние. Эта поправка носила название неравенства относительно Солнца и исправлялась по методу Гераклида при помощи введения дополнительной окружности — эпицикла, центр которой перемещался по эксцентру, в то время как сама планета совершала движение по эпициклу.

Напомним, что до Птолемея рассматривали только движение планет по долготе, он же создал методику расчета движения планет по широте, которая, между прочим, была почти полностью принята Коперником. Можно поставить вопрос о точности, которую обеспечивала методика Птолемея, т. е. сравнить положение планеты, вычисленное Птолемеем, с тем, которое можно рассчитать современными методами при помощи специальных астрономических таблиц. Результаты получаются почти совпадающими.

Казалось, что астрономы должны были бы радоваться, но тут случилось непредвиденное. В предшествовавший период развития астрономии были усовершенствованы инструменты, появились армиллы, при помощи которых можно было измерять на небе углы в различных плоскостях, разработана астрономическая терминология (долгота, широта, меридианы, параллели, склонение, прямое восхождение и т. д.), принят вавилонский способ измерения углов в градусах, минутах и даже секундах. Еще около 300 г. до н. э. астрономы Аристилл и Тимохарис произвели инвентаризацию звезд, переписав их названия и установив координаты — широту и долготу — каждой. Через 150 лет Гиппарх повторил определение координат и обнаружил любопытное явление: в то время как широты практически остались неизменными, долготы светил увеличились примерно на 2 градуса, что, конечно, далеко превышало допустимые пределы погрешностей. Эта работа была еще раз проделана Птолемеем, причем оказалось, что отмеченное Гиппархом явление, так называемая прецессия (или предварение равноденствий), действительно существует и долгота неподвижных звезд изменяется примерно на 1 градус в столетие — неподвижные звезды оказались движущимися! Астрономы последующих четырнадцати веков — от Птолемея до Коперника — получили трудную задачу: как объяснить это движение?

Для астронома средневековья после Птолемея планетная система рисовалась в следующем виде.

Землю окружают семь планетных сфер: Луны, Меркурия, Венеры, Солнца, Марса, Юпитера и Сатурна — с необходимыми для осуществления их движения эксцентрами и эпициклами; сферы иногда понимались как чисто геометрические (идеальные), но иногда также и как материальные. Эти планетные сферы окружала восьмая сфера — заведомо материальная («из чистого хрусталя»), к которой были прикреплены неподвижные звезды. Размеры этой сферы были огромными, но все же конечными, она совершала вращательное движение вокруг полюсов Земли, делая один оборот за 24 часа. На этой сфере помещался Первый Двигатель, сообщавший движение ей и всем остальным планетным сферам. Что же было вне восьмой сферы? Философы отвечали: бесконечные пространства, заполненные тонкой материей — эфиром. Средневековая церковь Давала иной ответ: вне этой сферы помещается эмпирей, царство бога, небесных существ (ангелов, архангелов и т. д. — до херувимов и серафимов включительно), а также блаженные души добродетельных людей и святых. Астрономы во избежание неприятностей предпочитали не развивать этого вопроса, находящегося вне сферы их ведения. Но тогда возник следующий вопрос: если восьмая сфера кроме суточного вращения имеет еще прецессионное, то должна быть и еще одна сфера — девятая, которая должна сообщать это движение.

Сравнение видимого движения по небу планеты Марс. а — для 297/6 г. до н. э.; б — для 274 г. до н. э.; в — для 235/4 г. до н. э. Вычислено по «Альмагесту» Птолемея (жирная линия) и современными методами (тонкая линия). По оси абсцисс отложена долгота, по оси ординат — широта по отношению к эклиптике. Поскольку обе линии близки к совпадению, их пришлось сместить одну относительно другой, приняв разные положения точек весеннего равноденствия

По теории, восходящей к Птолемею, кроме неподвижной Земли существовали еще неподвижные небесный экватор и эклиптика с двумя неподвижными точками пересечения, одна из которых — точка весеннего равноденствия — определяла начало тропического года. Вместо одной сферы неподвижных звезд появлялись две: одна из них, определявшая прецессионное движение (восьмая сфера), совершала полный оборот вокруг оси, проходящей через полюсы эклиптики, за 36 тыс. лет¹; девятая же сфера, к которой были прикреплены неподвижные звезды, делала вокруг полюсов Земли один оборот в сутки.

Наряду с этим возник еще один вопрос. Светило движется равномерно по окружности, центр которой не совпадает с центром Земли. Если мы соединим оба эти центра прямой и продолжим ее до пересечения с орбитой светила, то получим так называемую линию апсид. На одном ее конце светило будет находиться дальше всего от Земли, в так называемом апогее, а на другом — в наименьшем расстоянии от нее — в перигее. Определение апогея Солнца было сделано Гиппархом и повторено Птолемеем. Они получили различные положения, но поскольку при вычислениях приходилось измерять разность времен в днях, то измерения нельзя назвать особенно надежными. Величина, полученная Гиппархом, случайно оказалась более близкой к истинной, чем полученная Птолемеем, поэтому некоторые критики даже обвиняли Птолемея (несправедливо) в неумении наблюдать. Таким образом возник вопрос, является ли апогей светила постоянным или он тоже движется и в какой мере его движение зависит от прецессии. По изложенной теории Птолемея, он должен был быть постоянным. В своих звездных каталогах Птолемей отмечал положение апогея для различных светил, но в общей постановке вопрос оставался открытым. Равным образом нельзя было сказать, является ли прецессионное движение равномерным или нет.

Первые изменения в предложенную Птолемеем теорию внесли в IX в. н э. работавшие в доарабском астрономическом центре Харране Сабит ибн-Корра и аль-Баттани (Альбатегний). Первый считал, что прецессионное движение не является равномерным, более того, что оно может совершаться в обе стороны, т. е быть колебательным. Эта так называемая теория трепидации, или либрации, не пользовалась большим успехом среди мусульманских ученых, так как предложенная Сабитом амплитуда в 8 градусов оказалась уже превзойденной. Вопрос остался нерешенным, равно как и другой вопрос: сохраняет ли постоянную величину угол между эклиптикой и экватором? Работавший несколько позднее (ок. 828 г.) аль-Баттани установил перемещение апогейной точки Солнца, а также нашел более точную величину прецессии, а именно 1 градус не за 100, а только за 70 лет². В связи с этим он изменил данную Птолемеем величину продолжительности тропического года и одновременно подтвердил предположение о неизменности его продолжительности, что отрицало теорию трепидации.

Еще одна теория была разработана в XI в. толедским астрономом аз-Заркали (Арзахелем). Он посвятил много времени и труда, чтобы выяснить перемещение солнечного апогея как относительно равноденственных точек вследствие прецессии, как считал аль-Баттани, так и относительно неподвижных звезд (истинное движение). Последнее хотя и гораздо меньше прецессионного, но все же существует.

Таково было положение астрономии в эпоху, предшествующую Копернику, или, точнее, расцвету деятельности Краковского университета. Теперь нам нужно нарисовать образ Коперника как астронома в тот момент, когда он приступил к работе, коренным образом изменившей дальнейший ход астрономии. Подчеркнуть основные положения его теории астрономии тем более важно, что на этот счет существуют некоторые предвзятые мнения, объясняющие Коперника с точки зрения XIX—XX вв., но не с точки зрения XVI в.

Первое основное положение его теории: все движения небесных тел должны быть круговыми равномерными или составленными из таковых.

Второе положение заключалось в следующем: весь технический аппарат планетной астрономии должен строиться по Птолемею.

В написанном в 1524 г. послании к Ваповскому против Вернера Коперник говорит:

«...Мы... должны идти по стопам древних математиков и держаться оставленных ими как бы по завещанию наблюдений. И если кто-нибудь, наоборот, хочет думать, что верить им не следует, то, конечно, врата нашей науки будут для него в этом вопросе закрыты и он, лежа у порога, будет во сне больных грезить о движении восьмой сферы, и вполне заслуженно, ибо он клеветой на древних хотел помочь собственным галлюцинациям»³.

Третье его положение сводится к тому, что каждая новая теория должна строиться на основании наблюдений и прежде всего собственных. Ему понадобилось десять лет (с 1515 по 1525 г.), чтобы при помощи собственных наблюдений создать и новую теорию прецессии, и соответственно с ней методику расчета видимого движения Солнца.

Четвертое — не только положение, но даже основное правило его деятельности заключается в том, что исследовательская работа должна обязательно быть доведена до чисел, больше того, даже до таблиц. Он даже хотел ограничиться таблицами, и лишь настоятельные просьбы друзей заставили его написать большую книгу о своих исследованиях.

Примечания

1. По современным измерениям — за 26 тыс. лет.

2. По современным данным — за 69,5 лет.

3. Николай Коперник. О вращениях..., стр. 433.