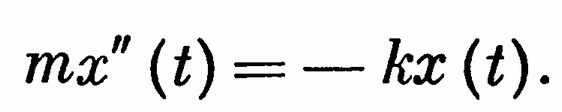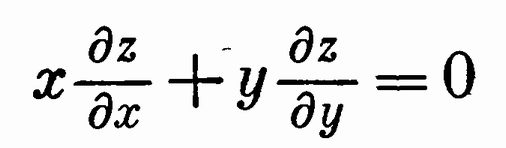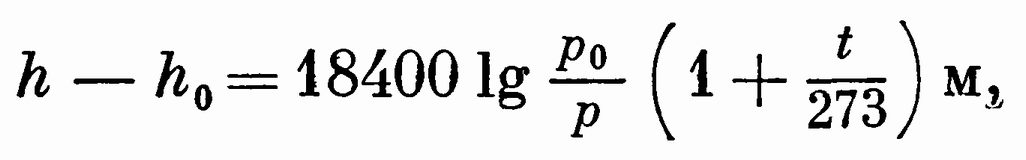Еще о математике Лапласа

Для интересующихся математикой приводим краткую дополнительную справку о математических работах Лапласа.

Прежде всего обратимся к дифференциальному уравнению Лапласа. Прибегая постоянно к аналитическому математическому методу при решении задач теоретической физики и механики, в частности — небесной механики, т. е. механики взаимодействия небесных тел, Лаплас попутно развивал математические методы.

Если, например, обозначить через x(t) величину отклонения тела от положения равновесия в момент t, то ускорение движения тела в этот момент выражается второй производной x″(t). Сила mx″(t), действующая на тело массы m при небольших растяжениях пружин, по законам теории упругости пропорциональна отклонению. Приходим к дифференциальному уравнению

В этом примере мы имеем одну независимую переменную. При большом числе переменных возникают частные производные. Уравнение

есть уравнение с двумя частными производными. Уравнения, подобные первому из приведенных, содержат одну производную первого порядка х″ и являются обыкновенными дифференциальными уравнениями второго порядка, а второе уравнение — дифференциальным уравнением с частными производными второго порядка. Они часто встречаются в задачах теоретической физики.

Дифференциальное уравнение с частными производными второго порядка, с тремя произвольными переменными x, у, z и искомой функцией u = u(х, y, z) называется уравнением Лапласа. Оно рассмотрено им в 1782 г. в работах по теории тяготения. К нему приводится решение и других задач физики и техники. Уравнению Лапласа удовлетворяет установившаяся температура и электрический потенциал внутри однородного тела, потенциал поля тяготения в области, не содержащей притягивающих масс, и т. п.

Далее к работам Лапласа по математике мы не будем возвращаться и здесь суммируем для интересующихся более специальные его исследования, выполненные в разное время.

Фундаментальными являются его работы по дифференциальным уравнениям, в частности первые общие методы интегрирования уравнений в частных производных (метод каскадов), а также метод производящих функций и так называемое преобразование Лапласа, с особенным успехом применяемое в теории вероятностей. В алгебре ему принадлежит знаменитая теорема о представлении определителей при помощи сумм произведений дополнительных миноров. Лаплас ввел в науку важные шаровые функции. Он является основателем современной теории вероятностей, составляющей математическую основу изучения статистических закономерностей в явлениях природы и общества. О ней мы поговорим дальше.

Здесь же отметим, что в области физики Лаплас разработал теорию капиллярности, дал правильную формулу для скорости звука в воздухе, вывел барометрическую формулу, которая позволяет определять разность высот двух пунктов или высоту над уровнем моря h —h₀:

где р и р₀ — давление атмосферы на этих уровнях, а t — средняя температура слоя воздуха в градусах Цельсия. Формула эта имеет широчайшее применение. Лаплас установил также закон взаимодействия между элементом тока и магнитным полюсом, вывел формулу для поверхностного натяжения жидкостей и провел ряд других исследований.