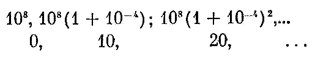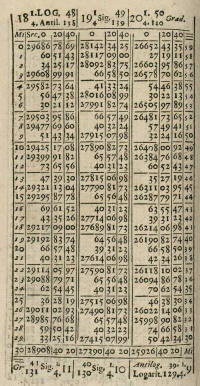
Ю.А. Белый

Иоганн КЕПЛЕР

1571-1630

Глава одиннадцатая

Кеплер и техника вычислений

Если учесть объем вычислительной работы, выполненной Кеплером только в поисках закономерностей движения планет, которые изложены им в «Новой астрономии», то уже одного «того вполне достаточно для признания его крупнейшим вычислителем своего века. Но помимо огромной работы, выполненной Кеплером при проверке многих гипотез, сменявших одна другую на его пути к истине, в актив его входят и «Рудольфинские таблицы», и «Эфемериды», и ряд других сочинений — результат соединения творческой мысли гения с тысячами часов упорной, утомительной и изматывающей вычислительной работы, для выполнения которой Кеплер не располагал (ад небольшими исключениями) ни штатом помощников, ни минимальными техническими средствами.

Поэтому никто лучше Кеплера не мог понять и оценить важность разработки и совершенствования методов и средств, направленных на облегчение, упрощение, а главное, ускорение вычислительной работы.

Как раз в это время в связи с общими требованиями к количественному анализу в условиях ускоренного развития науки и производства, в связи с потребностями мореплавания и повышением точности астрономических наблюдений, повлекшим за собой усложнение математических выкладок при их обработке, внимание видных математиков и вычислителей-практиков к проблемам совершенствования вычислений все более усиливалось.

Еще французские математики Н. Орем (вторая половина XIV в.) и Н. Шюке (конец XV в.), а также немецкий математик М. Штифель (середина XVI в.) заметили интересную зависимость между членами геометрической прогрессии и составленными из их показателей членами арифметической прогрессии, заключающуюся в том, что умножению, делению, возведению в степень и извлечению корня в первом ряду соответствует сложение, вычитание, умножение и деление во втором.

Эта идея могла быть использована для сведения арифметических операций к более простым при помощи таблиц, в которых последовательность степеней чисел сопоставлялась бы с последовательностью их показателей. Составление таких таблиц началось в конце XVI (Непер) — начале XVIIв. (Бюрги).

Шотландский математик Джон Непер опубликовал свои таблицы в 1614 г. под названием «Mirifici logarithmorum canonis descriptio) («Описание удивительных таблиц логарифмов»). Здесь он приводит семи- и восьмизначные значения логарифмов синусов, косинусов, а также тангенсов углов первой четверти. Приняв sin 90° равным 10⁷ = 10000000 (десятичные дроби тогда еще не получили широкого распространения), Непер определил свои логарифмы так, чтобы log_Ne10⁷ = 0 (log_Ne = логарифм Непера), логарифмы любых других значений синуса у него положительны (но уменьшаются при увеличении аргумента). Зависимость между неперовыми и натуральными логарифмами можно выразить так:

log_NeN ~ 10⁷ * ln 10⁷/N

Правила логарифмирования у Непера более громоздки, чем известные нам еще в школе, так как в них log_Ne1 ≠ 0.

В своих таблицах Непер не дал правил вычисления логарифмов, и лишь после его смерти в 1619 г. была опубликована книга («Устройство удивительных таблиц логарифмов»), где были приведены соответствующие указания.

Неперовы таблицы заинтересовали многих. По совету Непера английский математик Г. Бриге вычисляет четырнадцатизначные десятичные логарифмы чисел от 1 До 1000 (в 1617 г.), а затем четырнадцатизначные же от 1 До 20 000 и от 90 000 до 100 000 (в 1624 г.), лондонский преподаватель математики Джон Спейдель в 1617 г. составляет первую таблицу натуральных логарифмов. В 1625 г. англичанин Эдмунд Гунтер (Гюнтер), корреспондент Кеплера, изобретает логарифмическую шкалу — прообраз логарифмической линейки.

Но еще до того, как Ηепер издал свои первые таблицы, на несколько другой основе были составлены таблицы Йостом Бюрги.

Бюрги, выходец из Швейцарии, талантливый механик-самоучка, в 1579—1603 гг. состоял часовщиком и механиком у ландграфа Вильгельма VI Гессенского, одного из немногочисленных (наряду с Альфонсом X и Улугбеком) самодержавных властителей, сочетавших государственную деятельность с плодотворными научными занятиями. Бюрги помогал ландграфу строить и ремонтировать астрономические инструменты в обсерватории в Касселе. Имеются сведения, что в 1588—1597 гг. Бюрги сам принимал участие в астрономических наблюдениях. Для их обработки Бюрги составлял таблицы синусов. После смерти Вильгельма Бюрги переехал в 1603 г. в Прагу и с 1603 по 1622 г. состоял придворным часовщиком и механиком сначала у Рудольфа II, а затем у его преемников.

Таким образом, по меньшей мере десять лет, с 1603 по 1612 г., Бюрги жил в одном городе с Кеплером, был хорошо с ним знаком и по роду своей деятельности непосредственно связан. Кеплер написал даже весьма обстоятельное предисловие к составленным Бюрги таблицам синусов, но оно, как и сами таблицы, осталось неопубликованным и хранится сейчас в числе других рукописей Кеплера в Архиве АН СССР.

Уже около 1610 г. Бюрги составил свои вычислительные таблицы. В этих таблицах членам геометрической прогрессии вида а_к = 10⁸(1 + ¹/10⁴)^k; К = 0, 1, 2, 3,... он ставил в соответствие члены арифметической прогрессии 0,10, 20,... Получалось два ряда

В изданной позже книге числа нижнего ряда были напечатаны красной краской («красные числа»), а числа верхнего ряда — черной («черные числа»). Таким образом, красные числа представляли собой логарифмы черных, деленных на 10⁸ при основании 1,0001. Таблицы Бюрги являлись по существу таблицами антилогарифмов (черных чисел). Бюрги был бы признан создателем первых таблиц логарифмов, если бы опубликовал их сразу же после составления, но нерешительность, «медлительность и скрытность», в чем его позже недвусмысленно упрекнул Кеплер, стоила ему приоритета. Более того, он, видимо, хранил втайне свою работу даже от близких и заинтересованных лиц, в том числе и от Кеплера.

Только в 1620 г,, через шесть лет после Непера, Бюрги публикует свои таблицы под названием «Arithmetische und Geometrische Progress-Tabulen sambt gründlichen Unterricht, wie solche nützlich in allerlev Rechnungen und verstanden werden soll», т. е. «Таблицы арифметической и геометрической прогрессии вместе с основательным руководством, как их понимать и с пользой употреблять во всяческих вычислениях».

Работа эта была напечатана не по настоянию Кеплера, как это иногда утверждается*, а без его ведома, и трудно сказать, когда Кеплер узнал о ее выходе из печати. Не исключено, что он этой работы вообще не видел.

Заметим, что объявленное в названии книги Бюрги «руководство» странным образом из нее выпало, но оно действительно было написано Бюрги и обнаружено в рукописи только в середине ХIХ в.

Таблицы Бюрги, появившиеся позже таблиц Непера и более удобных для вычисления таблиц десятичных логарифмов Бригса, не получили распространения и в наше время представляют лишь исторический интерес, но имя Бюрги постоянно соседствует с именем Непера. Роль же Кеплера в истории развития логарифмических вычислений зачастую недооценивается. Между тем совершенно естественно, что, будучи столь заинтересованным в совершенствовании средств вычислений, Кеплер не мог пройти мимо столь важного изобретения. Впервые таблицы Непера Кеплер увидел во время короткого пребывания в Праге весной 1617 г. у кого-то из знакомых, но тогда ему пришлось ограничиться лишь беглым просмотром, как он об этом пишет Мёстлину в декабре 1618 г.¹ О своем впечатлении от этого беглого обзора он сообщает В. Шикарду: «Некий шотландский барон, имя которого я не запомнил, выступил с блестящим достижением, в котором он каждую задачу на умножение и деление превращает в чистое сложение и вычитание без применения синусов (как простаферетики**). Вместо этого он использует таблицы тангенсов, и утомительное умножение и деление везде уступает простоте, краткости и легкости сложения и вычитания»².

Значит, при первом кратком знакомстве с таблицами Непера Кеплеру показалось, что средняя колонка в этих таблицах под названием «Differentiae», представлявшая собой разности логарифмов синусов дополнительных углов, т. е. логарифмы тангенсов, предназначалась только для замены синусов.

Только в июле 1619 г. таблицы Непера попадают, наконец, непосредственно к Кеплеру. Но уже до этого Кеплер смог с ними подробнее познакомиться по книге берлинского преподавателя математики Вениамина Урсинуса, бывшего своего помощника в Праге и Линце, вышедшей в 1618 г. под названием «Cursus mathematici practici, vol.1», т. е. «Курс практической математики, том I». Урсинус привел таблицы Непера почти без изменения, сократив лишь аргументы и их логарифмы на два знака и приложив к ним краткое объяснение. Теперь Кеплеру стала ясной сущность изобретения и его важность для ускорения вычислительных работ, и он немедленно приступает к разработке собственной теории вычисления логарифмов, составлению логарифмических таблиц и их использованию в практических вычислениях на решающем этапе составления рудольфинских планетных таблиц. Об этом Кеплер пишет в начале декабря 1619 г. в письмах к Ремусу и Мёстлину. Воодушевленный изобретением Непера, он с благоговением посвящает тому свои «Эфемериды» на 1620 г., не зная, что Непера уже два года как нет; в живых.

Что же касается работы Бюрги, то Кеплер до издания «Рудольфинских таблиц» ни разу о его имени в этом плане не упоминает. Объективность Кеплера но отношению к чужому вкладу в развитие науки не вызывает сомнения и вполне соответствует его собственным словам: «Я всегда придерживался правила восхвалять то, что другие, по моему мнению, сделали хорошо... Я никогда не пренебрегал чужими знаниями и не утаивал их, где мне не хватало своих»³. Единственное замечание но этому поводу содержится на 11-й странице «Рудольфинских таблиц», изданных в 1627 г. Здесь Кеплер пишет: «...Йост Бюрги указал путь к точно таким логарифмам задолго до публикаций Непера». И продолжает: «...Правда, его медлительность и скрытность загубила новорожденного вместо того, чтобы привлечь его для всеобщей пользы»⁴. В этих словах Кеплера слышен упрек. Становится ясно, что хотя Кеплер и знал о работе, которую Бюрги вел в пражские годы, но лишь в самых общих чертах, и сообщенное ему Бюрги не выходило за пределы неопределенных намеков. И еще один довод в пользу этого мнения: рассматривая в конце 1623 г. логарифмы Бригса, Кеплер видит их преимущество перед неперовыми и своими в том, что при увеличении аргументов логарифмы их здесь возрастают. Но ведь тем же (и, кстати, единственным) преимуществом обладали и логарифмы Бюрги и, зная это обстоятельство, Кеплер не преминул бы об этом упомянуть. Выходит, что до конца 1623 г. Кеплер вряд ли знакомился с «Таблицами прогрессий» Бюрги.

В противоположность Бюрги, Кеплер сообщает о ходе работ над составлением собственных таблиц многим друзьям и знакомым и старается перетянуть их в число сторонников новых методов вычислений. Это не всегда было просто. Мёстлин, например, в запоздалом ответе Кеплеру на письмо от 3 декабря 1618 г. в марте 1620 г. пишет: «Хотя я вижу, что [логарифмические] вычисления дают верные результаты, я к ним все же не стану обращаться, так как я до сих пор не обнаружил их основ, так что я подозреваю, что изобретатель умышленно в качестве «фундаментального числа»*** взял какое-то запутанное число, обоснование которого очень тяжело, если не невозможно. Я считаю недостойным математика желание смотреть чужими глазами и опираться на что-то или выдавать за доказанное то, чему он сам не имеет доказательства»⁵. Кеплер немедленно по получении письма Мёстлина принимается за разработку основных положении теории построения логарифмических таблиц и излагает ее в длинном письме Мёстлину, начатом 12 апреля, а законченном только 19 июня 1620 г.⁶ В эти сроки Кеплер и решил самостоятельно вопрос о построении логарифмических таблиц.

Отметим, что изданную посмертно, в 1619 г., книгу Непера об устройстве таблиц логарифмов Кеплер увидел только летом 1621 г., купив ее в Тюбингене во время длительного пребывания в Вюртемберге в связи с судом над его матерью.

Непер подходил к образованию логарифмов чисел на основе геометрических, можно сказать, кинематических соображений. Две точки перемещаются прямолинейно и параллельно, но в то время, когда одна из них, скажем у, движется равномерно от нуля, вторая — x движется замедленно со скоростью, пропорциональной ее расстоянию до конечной точки своего движения, причем начальная точка имеет значение 10⁷. Неперов логарифм числа x, соответствующего расстоянию от x до конечной точки ее движения, равен расстоянию точки у от начала ее движения. При x = 10⁷ у = 0, т. е. неперов логарифм 10⁷ = 0. Когда числа x_i образуют арифметическую прогрессию, то их неперовы логарифмы образуют убывающую геометрическую прогрессию. Таблицы Непера предназначались для облегчения действий с тригонометрическими величинами и были неудобны для действий с числами в десятичной системе счисления.

Этому наглядному геометрическому обоснованию логарифмов Кеплер противопоставляет чисто арифметическое, более естественное и соответствующее этимологическому значению термина «логарифм» (λόγοσ — здесь отношение, αριθμός—число). Кеплер пишет, что для него логарифмы не связаны «собственно с категориями линий, движения или протекания, или с любыми другими чувственными качествами, а если так можно сказать, с категорией отношения и мыслительными качествами»⁷.

В соответствии с этим Кеплер исходит из следующих соображений:

Однако более существенно то обстоятельство, что в отличие от Непера Кеплер предназначал свои логарифмы прежде всего для облегчения вычислений над натуральными числами в десятичной системе счисления. Таблицы логарифмов Кеплера состояли из тысячи строк — по одной на каждое число и на его логарифм (отсюда и название книги: «Ghilias Logarilhmorum» — «Тысяча логарифмов»). В каждой строке — пять данных. В первой колонке — дуги окружности α в частях круга зодиака (по 30°), градусах, минутах и секундах. Так, 280° 20' 11" записано как 9^s 10°20'11", или просто 9.10.20.11. Во второй колонке (основной, с постоянным шагом) приводятся абсолютные числа N от 1 до 1000, они же и синусы дуг, приведенных в первой колонке (N = sin α), третья колонка отведена на доли суток в часах, минутах и секундах (N.24.0.0.), в четвертой помещены восьмизначные кеплеровы логарифмы с табличными разностями (Log_kN) (кстати, обозначение Log введено в обращение Кеплером), наконец пятая отведена на числа в шестидесятиричной системе счисления (N.60.0). Логарифмов тангенсов в таблицах Кеплера нет, что создает определенные неудобства.

Тюбингенский профессор В. Шикард, который одним из первых познакомился с таблицами Кеплера, пишет ему 30 сентября 1624 г.:

«Я радуюсь, что они [логарифмы] стали доступны всем, и поздравляю сам себя с таким прекрасным средством вычислений. Они будут мне полезны и для других вычислений, так как упорядочены по числам от 1 до 1 000. В связи с этим я предпочитаю их этим логарифмам Непера. Но не стану скрывать истины, в тригонометрии я использую охотнее неперовы таблицы в связи с тем, что для синусов они составлены до целых минут, в то время, как в твоих нужно приведение и отыскивание пропорциональных частей, что значительно задерживает и неудобно, когда приходится спешить»⁸.

Это неудобство Кеплер частично устраняет уже в «Рудольфинских таблицах», где вводит раздельные таблицы для логарифмов чисел и логарифмов тригонометрических величин.

Рукопись «Тысячи логарифмов» была готова уже зимой 1621/22 г. Кеплер намеревался напечатать ее в Тюбингене и послал Мёстлину с просьбой осуществить контроль и корректуру при печатании. У того она оставалась почти полтора года без движения, и Кеплер вынужден был обратиться к Шикарду с просьбой забрать рукопись у Мёстлина и переслать ее ландграфу Филиппу Гессенскому, астроному-любителю, интересовавшемуся логарифмическими вычислениями и предложившему свою помощь и средства для издания кеплеровых таблиц. После этого Кеплер долго ничего не слышал о судьбе своей рукописи и неожиданно узнал из каталога осенней книжной ярмарки 1624 г., что его «Тысяча логарифмов» издана в Марбурге и появилась в продаже. Это было для Кеплера несколько неожиданно и даже неприятно, так как им было написано руководство к применению таблиц, содержавшее и элементы теории логарифмов, но, не зная о судьбе и точном нахождении рукописи, он не стал посылать то, что должно было составлять с «Логарифмами» одно целое. Позже тот же Филипп Гессенский организует издание и этого руководства под названием «Supplementiim Chilias Logarithmorum» («Дополнение к тысяче логарифмов»), которое появилось в продаже уже на осенней ярмарке 1625 г.

Таблицы Бюрги в практических вычислениях вряд ли вообще кем-нибудь использовались. Таблицы Непера быстро устарели и были заменены более удобными таблицами десятичных и натуральных логарифмов. Таблицам Кеплера повезло больше: с их помощью вычислялись рудольфинские таблицы планетных движений — это был, пожалуй, первый случай основательного применения логарифмических таблиц на практике, и коль скоро сами кеплеровы таблицы логарифмов в несколько переработанном виде вошли в состав рудольфинских, служивших астрономам настольной книгой на протяжении более 100 лет, это и обеспечило кеплеровым логарифмам сравнительно длительную жизнь.Кроме того, сами кеплеровы таблицы неоднократно переиздавались. Последнее издание их вышло уже в начале XVIII в., в 1700 г.⁹

Итак, в истории логарифмов Кеплеру принадлежит разработка оригинальной теории построения логарифмических таблиц, составление с ее помощью и издание собственных таблиц, позже неоднократно переиздававшихся, их плодотворное и многократное применение в весьма важных астрономических вычислениях. В общей сложности таблицы Кеплера издавались не менее четырех раз на протяжении более чем 75 лет.

Вклад Кеплера в распространение новых средств вычислений мог быть бы и более существенным. В составе приобретенного в конце XVIII в. Петербургской Академией наук обширного собрания рукописей Кеплера, о чем еще будет идти речь впереди, обнаружена подготовленная к печати, но по неизвестным причинам оставшаяся неопубликованной, рукопись на немецком языке под названием «Der Zahlen Inventarium» («Опись числам»)¹⁰. Хотя чистовой экземпляр этой рукописи и не принадлежит руке Кеплера, его авторство сомнений не вызывает: им лично выполнена правка текста, в полном заголовке имеется ссылка на «Тысячу логарифмов», все рассмотренные примеры опираются на его логарифмы. Наконец, в том же собрании обнаружен черновик этой работы¹¹, написанный Кеплером собственноручно. Из текста видно, что Кеплером готовилось издание таблиц логарифмов целых чисел на немецком языке, которое должно было сыграть ту же роль для распространения математических знаний среди широких слоев населения германских земель, какую имел подготовленный самим же Кеплером перевод на немецкий язык его «Новой стереометрии винных бочек». По неизвестным причинам это издание осуществлено не было.

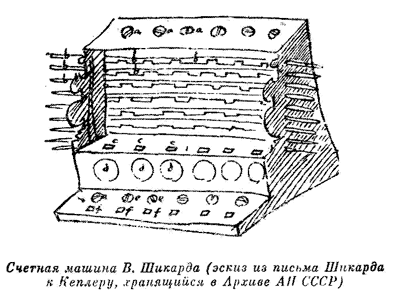
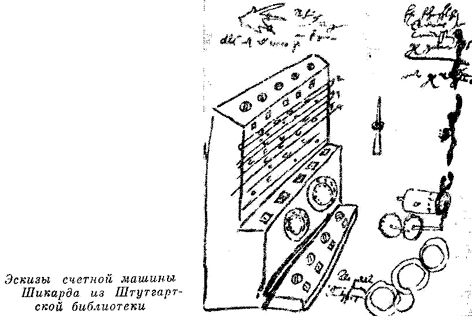
Однако сказанным не исчерпывается роль Кеплера в развитии вычислительных средств. Совсем недавно изучение рукописного наследия Кеплера, хранящегося в Архиве АН СССР в Ленинграде, позволило раскрыть интереснейшую страницу истории развития механизированных вычислений, к которой Кеплер имел весьма важное и непосредственное отношение.

До последнего времени было принято считать, что первую механическую вычислительную машину в современном понимании этого слова изобрел в 19-летнем возрасте французский философ, физик и математик Влез Паскаль. В машине Паскаля был предусмотрен автоматический перенос десятков, но с ее помощью можно было производить лишь сложение и вычитание, да и то с большими неудобствами.

Однако среди упомянутых рукописей обнаружено любопытное письмо тюбингенского профессора Вильгельма Шикарда от 25 февраля 1624 г., в котором приводится эскизное изображение вычислительной машины, построенной им за два десятилетия до Паскаля¹².

С Шикардом Кеплер познакомился не позже 1617 г., когда тот был профессором восточных языков в Тюбингенском университете. Заметив в молодом ученом незаурядные математические способности, Кеплер настоял на углубленных занятиях Шикарда математикой, о чем сам Шикард говорит в своем письме Кеплеру от 30 сентября 1617 г.¹³, хранящемся в том же собрании. Шикард последовал совету Кеплера. Из приведенного выше отрывка его письма видно, что он уже в 1624 г. широко использовал для вычислений логарифмические таблицы Кеплера. После смерти Мёстлина Шикард стал его преемником на посту профессора математики в Тюбингенском университете.

К сожалению, не сохранились письма Кеплера к Шикарду того периода, но с большой вероятностью можно утверждать, что именно Кеплер, больше других ощущавший необходимость разработки новых вычислительных средств, посоветовал Шикарду подумать над возможностью создания вычислительной машины, а может быть, сообщил ему и некоторые свои идеи по этому поводу. Не случайно, что именно с Кеплером Шикард регулярно переписывался в процессе работы над своим изобретением.

В письме от 20 сентября 1623 г.¹⁴ Шикард сообщает Кеплеру, что им построен первый образец машины, которая выполняет четыре арифметических действия, т. е. не только складывает и вычитает, но и умножает и делит, и притом действует хорошо.

Из следующего, уже упоминавшегося письма от 25 февраля 1624 г. явствует, что Шикард готовил экземпляр машины и для Кеплера. Видимо, Кеплер в недошедших до нас письмах заказал экземпляр машины для себя. К сожалению, машину Кеплер не получил: оба изготовленных экземпляра сгорели при пожаре. Однако эскиз машины, содержащийся в письме, позволяет судить о ее внешнем виде, а эскиз, обнаруженный недавно в библиотеке города Штутгарта, дает представление о ее устройстве¹⁵. В конструкции машины применялось 11 счетных колес, точнее, шестерен, с 10 зубьями каждое, б однозубых колес (для переноса десятков), 6 цилиндрических валиков, на которых была выгравирована таблица умножения с особым расположением множителей, 6 рычагов для установки чисел (по одному на разряд) и 9 задвижек с окнами. Машина состояла из суммирующего механизма, устройства для умножения и устройства для фиксации промежуточных результатов.

В суммирующем устройстве использовались зубчатые передачи: на шесть параллельных осей насаживалось по одной десятизубой и по одной однозубой шестерне, с помощью последней осуществлялся перенос в старший разряд полного десятка из младшего, а также по цилиндрическому валику, на образующей поверхности которого были выгравированы цифры от 0 до 9. При этом в соответственных окошках можно было видеть первое слагаемое (или уменьшаемое) при его установке и промежуточные или итоговые результаты сложения или вычитания. Деление производилось путем повторного вычитания делителя из делимого.

Для умножения фактически использовались палочки Непера****, свернутые в цилиндр. Хотя при этом приходилось выполнять промежуточное поразрядное сложение на суммирующем устройстве с фиксацией результатов, использование этого устройства для выполнения умножения и деления могло дать определенную экономию времени и снизить умственное напряжение вычислителя.

Машина Шикарда была сконструирована и построена в 1623-1624 гг., в разгар Тридцатилетней войны. Технические возможности для изготовления такого рода устройств были довольно низкими, трудно устранимый люфт между зубьями счетных колес ограничивал количество поразрядных узлов всего шестью разрядами. Низкий уровень техники массового производства стал позже препятствием в распространении вычислительных машин, созданных Паскалем и Лейбницем.

Результаты кропотливого труда Шикарда были уничтожены пожаром, а события бушевавшей в то время Тридцатилетней войны отвлекли внимание современников от этого интереснейшего изобретения. Безвременная смерть Кеплера в 1630 г., а затем и Шикарда (его сразила чума в 1636 г.) также сыграли свою роль в том, что в течение более чем 300 лет изобретение Шикарда оставалось совершенно неизвестным и о нем узнали лишь в результате изучения рукописей Кеплера, хранящихся в нашей стране.

Нам представляется весьма интересным и важным тот факт, что к этому значительно опередившему эпоху изобретению — первой ласточке на пути, который в наши дни привел к бурному развитию вычислительной техники, к появлению электронных вычислительных машин, быстродействие и производительность которых подавляют воображение, Кеплер имел несомненное и непосредственное отношение.

* Так утверждает, папример, И. Тропфке. См. /. Tropfke. Geschichte der Elementarmathematik in systematischer Darstellung, 2. Aufl. В. — Lpz., Bd. 2, 1923, S. 180.

** Простаферетические методы вычислений (греч. προσθεσις — прибавление, 'αφαιρεσις — вычитание) заключались в упрощении вычислительных процессов с тригонометрическими величинами путем преобразования произведения тригонометрических величии в сумму, например по формуле sin α * sin β = ¹/₂ [cos (α — β) — cos(a+ß)].

*** Под «фундаментальным числом» Мёстлин имеет в виду не основание системы логарифмов, понятие, в то время еще неизвестное, а число, близкое к log 1, которое в логарифмах Непера и Кеплера было отлично от нуля.

**** Это оригинальное приспособление для облегчения умножения было предложено Дж. Непером в 1617 г. в его книге «Rabdologiae, seu Numerationis per virgulas Libri duo. Edinburgi». Состоит оно из набора полосок, на каждой из которых помещены таблички умножения одноразрядных чисел на одноразрядные. Составляя по записанным в верхней части палочек числам любое многоразрядное число, очень просто найти его произведение на одноразрядное число, а при сложении суммы таких произведений— и результаты умножения на многоразрядное число. В настоящее время употребляются редко в связи с наличием более совершенных вычислительных средств.

Примечания

1. — Письмо Кеплера Мёстлину 3 декабря 1618 г. GW, XVII, 297.

2. — Письмо Кеплера Шикарду И марта 1618 г. GW, XVII, 218.

3. — «Dissertatio cum nuntio sidereo». Pragae, 1610, Ad lectorem admo-nitio. GW, IV, 286—287.

4. — «Tabulae Rudolphinae». Ulmae, 1627, p. 11. GW, X, 48.

5. — Письмо Мёстлина Кеплеру 2 марта (ст. ст.) 1620 г. GW, XVII, 423.

6. — Письмо Кеплера Мёстлину 19 июня 1620 г. GW, XVIII, 7—24.

7. — «Supplementum chiliadis logarithmorum». Marpurgi, 1625, p. 114. GW, IX, 355.

8. — Письмо Шикарда Кеплеру 30 сентября 1624 г. GW, XVIII, 214— 215.

9. — Логарифмические таблицы Кеплера, обработанные еще при его жизни его сотрудником и зятем Якобом Барчем, последний раз вышли отдельным изданием в 1700 г.: Joh. Kepleri et Jacobi Bartschii. Tabulae manuales logarithmicae ad calculum Astrono-micum, in specie Tab. Rudolphin a rum compendiose tractandum mire utiles... Curante Joh. Casp. Eisenschmid. Argentorati (=Strassburg), 1700.

10.- «Der Zahlen Inventarium oder Schottische Practica». Архив АН СССР, ЛО, ф. 285, оп. 1, № 5, лл. 157—163.

11. — Там же, № 18, лл. 103—105.

12. — Письмо Шикарда Кеплеру 25 февраля 1624 г. Архив АН СССР, ЛО, ф. 285, оп. 1, № 8, л. 229; № 16, л. 117 об. Опубликовано: GW, XVIII, 142—143.

13. — Письмо Шикарда Кеплеру от 30 декабря 1617 г. Там же, № 11, л. 211. Опубликовано: GW, XVII, 246—249.

14. — Письмо Шикарда Кеплеру 20 сентября 1623 г. GW, XVIII, 142— 143.

15. — См.: В . von Frey tag Löringhoff. über die erste Rechenmaschine. — «Physikalische Blätter», 14, 1958, S. 361—365.