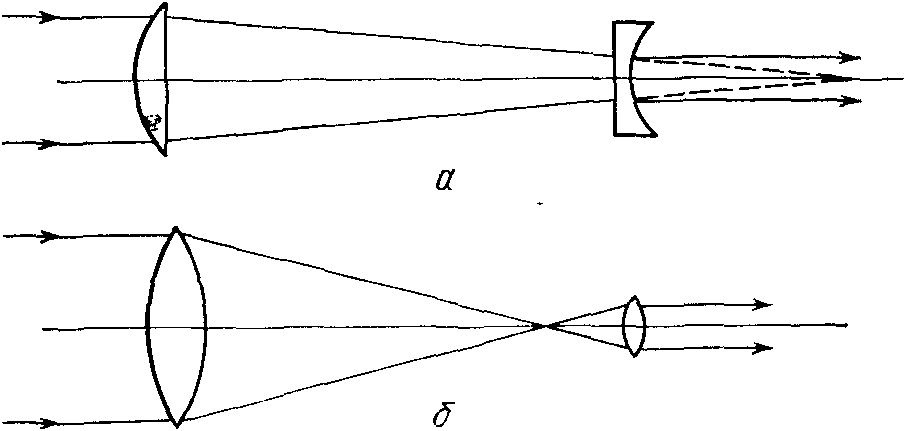
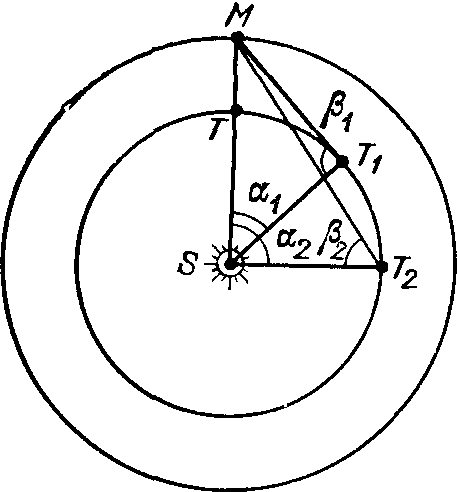
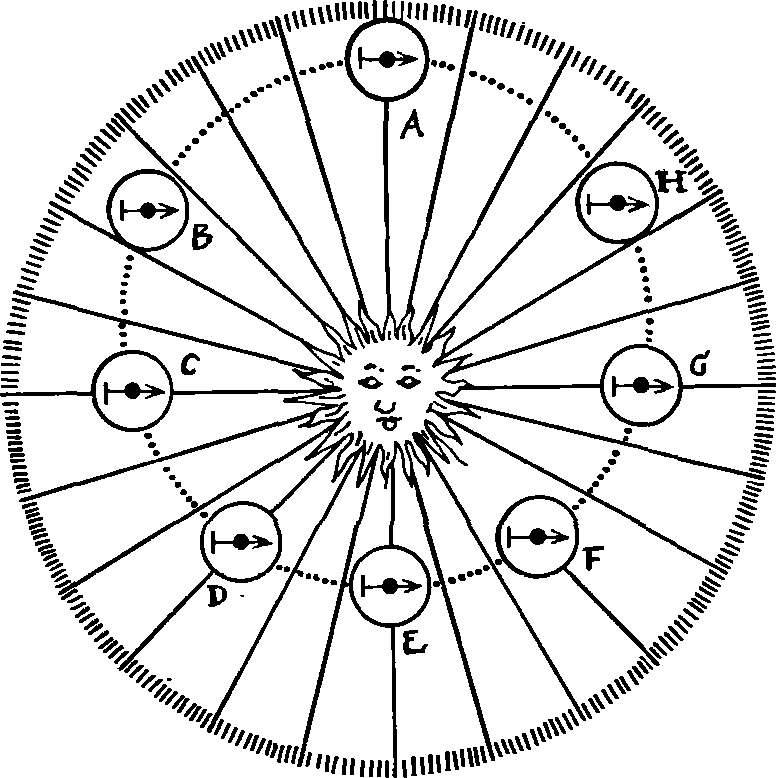
Он «вымел паутину с неба»

Коперник «сдвинул Землю» — поставил ее в один ряд с другими планетами. И все же его система мира еще оставалась загроможденной эксцентрами и эпициклами. Как сказал позже выдающийся английский физик Джеймс Клерк Максвелл (1831—1879), «необходимо было вымести эту паутину с неба». Эту нелегкую работу и выполнил «великий законодатель неба» Иоганн Кеплер на основании точных многолетних наблюдений Тихо Браге.

В слабом теле — могучий дух. «Он жил в эпоху, когда еще не было уверенности в существовании некоторой общей закономерности для всех явлений природы. Какой глубокой была у него вера в такую закономерность, если, работая в одиночестве, никем не поддерживаемый и непонятый, он на протяжении многих десятков лет черпал в ней силы для трудного и кропотливого эмпирического исследования движения планет и математических законов этого движения!». Так писал А. Эйнштейн о выдающемся немецком ученом Иоганне Кеплере, ученом, подготовившем для Ньютона почву для открытия закона всемирного тяготения.

Иоганн Кеплер родился 27 декабря 1571 г. в небольшом городке Вейль недалеко от Штутгарта. Его детские годы прошли в гнетущей бедности, на фоне грубых ссор родителей — солдата-наемника и неграмотной дочери сельского трактирщика. Вот что он писал о своих родителях: «...мой отец... Человек злобный, непреклонный, сварливый... 1589... оставив мать тяжело больной, он исчез из дому окончательно», мать была «низкого роста, смугла, болтлива и сварлива, с тяжелым характером»... В пятилетием возрасте Иоганн заболел оспой, на коже у него на всю жизнь остались незаживающие язвы. Из-за болезни печени и желудка он вынужден был все время соблюдать диету, его часто терзала лихорадка, мучили сильные приступы головной боли. У него была врожденная близорукость и так называемая монокулярная полиопия — болезнь, при которой, глядя на определенный объект (например на Луну), он видел не одно, а несколько его изображений. Поэтому, как справедливо отметил Ю.А. Белый, «нельзя не удивляться поразительной силе духа, таившегося в этом слабом теле, которая наперекор физическим страданиям и... крайне неблагоприятным условиям жизни и творческой деятельности позволила Кеплеру выполнить совершенно необычную по размаху работу и добиться столь выдающихся научных достижений»¹.

Уже в начальной школе Кеплер проявил незаурядные способности и получил возможность продолжать учебу: вначале в протестантской духовной семинарии, а с 1589 г. — в Тюбингенском университете, благодаря выплачиваемой властями города Вейля стипендии. Здесь под влиянием профессора математики и астрономии Михаила Мёстлина Кеплер увлекся астрономией, о чем он позже писал так: «Уже к тому времени, когда я внимательно следовал в Тюбингене преподаванию знаменитого Мёстлина, я ощутил, насколько несовершенно со многих точек зрения употребительное до сих пор представление о строении мира. Поэтому я был так сильно восхищен Коперником, о котором мой учитель очень часто упоминал на своих лекциях, что не только часто защищал его взгляды в студенческих диспутах, но и сам тщательно подготовил диспут на тему, что первое движение (вращение небесной сферы неподвижных звезд) проистекает от вращения Земли... я постепенно, отчасти из лекций Мёстлина, отчасти из собственных соображений, собирал все достоинства, которыми Коперник превосходит Птолемея с математической точки зрения».

Через два года Кеплер сдал магистерский экзамен и начал учебу на теологическом факультете. Однако в 1594 г. за несколько месяцев до. окончания полного курса сенат университета решил послать его как лучшего математика в г. Грац (Австрия) на вакантную должность учителя гимназии. Кеплер принял это решение крайне неохотно. В одном из писем Мёстлину он писал: «Я хотел стать теологом и долго пребывал в мучительном беспокойстве. Теперь я, однако, вижу, что при усердии могу прославить Бога и в астрономии». В обязанности Кеплера в Граце входило, кроме чтения лекций по математике, составление календарей; их он здесь составил шесть. Условия для научной работы были крайне плохими. Как заметил один из его высокопоставленных друзей, обстановка в провинции была малоблагоприятной, «знать проявляла поразительное невежество во всем, обладала варварской точкой зрения в своих суждениях, ненавидела науку и ничем меньше не интересовалась, чем учеными»... По поводу составления календарей и предсказаний в них астрологического характера Кеплер в одном из писем писал так: «Если я сочиняю календари и альманахи, то это, без сомнения, — прости мне, Господи, — великое рабство, но оно в настоящее время необходимо. Избави я себя хоть на короткое время от этого — мне пришлось бы идти в рабство еще более унизительное. Лучше издавать альманахи с предсказаниями, чем просить милостыню. Астрология — дочь астрономии, хоть и незаконная, и разве не естественно, чтобы дочь кормила свою мать, которая иначе могла бы умереть с голоду»... В таких условиях и появилась первая книга Кеплера — «Предвестник космографических исследований, содержащий космографическую тайну об удивительном соотношении пропорциональности небесных сфер, о причине числа небес, их величинах, о периодических их движениях, общих и частичных, объясненную при помощи пяти правильных геометрических тел» (Тюбинген, 1596 г.).

В апреле 1597 г. Кеплер женился на Барбаре Мюллер, дочери мельника, которую в дальнейшем, по-видимому, шокировало низкое общественное положение ее мужа, в его делах она ничего не понимала и не хотела понимать. Родившийся в феврале 1598 г. сын Генрих умер через два месяца от менингита, от той же болезни год спустя в возрасте одного месяца умерла дочь Сусанна. Начались преследования протестантов, и Кеплер вместе с семьей был вынужден искать пристанища в другом месте. И тут-то он получил приглашение Тихо Браге, который, познакомившись с «Космографическим вестником», понял, что именно Кеплер с его незаурядным математическим дарованием может превратить долгие ряды наблюдений в стройную теорию.

В начале 1600 г. Кеплер прибыл в Бенатек. Здесь Браге поручил ему обработку наблюдений Марса. Воодушевившись, Кеплер посчитал, что сможет решить проблему Марса за восемь дней, но... смог «укротить» его лишь через восемь лет. Впрочем, кто знает, как бы сложились отношения между двумя великими астрономами, — ведь они начали ссориться буквально сразу после приезда Кеплера к Тихо (со своими помощниками Тихо держал себя высокомерно, а Кеплер был так раздражителен...), но в октябре 1601 г. Тихо Браге умер. Кеплеру было присвоено звание «императорского математика» и установлена плата 500 гульденов в год (у Браге она составляла 3000 гульденов). Но за все 20 лет своей службы Кеплер получил всего 3/4 одного годичного заработка. Жил он со своей семьей в тяжелой бедности, зарабатывая на хлеб преподаванием математики, составлением календарей и гороскопов. В таких условиях он закладывал фундамент современной астрономии.

Кеплер прожил в Праге с 1600 по 1612 гг. После отречения от короны его «покровителя» императора Рудольфа II (1611 г.) положение Кеплера ухудшилось. Он предпринял попытку занять кафедру математики в Тюбингенском университете. Но консистория лютеран отказала ему на том основании, что он в свое время не согласился подписать так называемую «формулу согласия» — своеобразный кодекс лютеранства. В том же 1611 г., в феврале, умер от оспы его восьмилетний сын Фридрих, а в июле жена Барбара. В апреле 1612 г. Кеплер переезжает в г. Линц — столицу Верхней Австрии. Здесь главным его заданием было составление таблиц планетных движений — «Рудольфинских таблиц». В Линце его снова принуждают подписать «формулу согласия». Кеплер соглашается сделать это с оговоркой, что он не верит, будто в момент причастия Христос каким-то образом присутствует в хлебе и вине. В итоге Кеплер был исключен из лютеранской общины и его положение ухудшилось еще больше.

Невольно вспоминается, что подобная ситуация уже была десять лет назад. Он не согласился перейти в католическое вероисповедание, несмотря на то, что в этом случае обеспечил бы себе выгодное положение и благополучие. А ведь речь идет о человеке, который говорил о себе, что «он действительно набожен до суеверия»!

В Линце Кеплер женился вторично на Сусанне Рейттингер, сироте и бесприданнице, дочери столяра. И хотя с точки зрения линцского «общества» этот брак выглядел скандальным мезальянсом, Сусанна оказалась под стать своему мужу. Она с достоинством переносила все невзгоды и бедствия, и далее преследовавшие Кеплера, поддерживала его в трудный час. А бед было немало. Из семерых детей трое умерли в раннем детстве. В течение четырех лет он вел тяжелую борьбу против обвинения его матери в «колдовстве». В 1626 г. толпа окружила дом «еретика» в Линце, угрожая Кеплеру самосудом...

И вот Кеплер снова в Праге в поисках покровителя. И снова, в который уже раз, судьба искушает его. Стоило ему перейти в католицизм, и император Фердинанд обеспечил бы ему будущее. Но Кеплер этого не сделал. Ему удалось получить место у императорского военачальника Альбрехта Валленштейна, который хотел иметь «домашнего астролога». Так Кеплер в 1628 г. оказался в небольшом городке с 4000 жителей Сагане (теперь ПНР). Осенью 1630 г. Кеплер, чтобы попытаться получить жалованье, которое не выплачивалось ему в течение многих лет, отправился верхом в г. Регенсбург, где Фердинанд II собрал германских князей. Вскоре после, приезда в Регенсбург Кеплер тяжело заболел лихорадкой, болезнь быстро прогрессировала, и 15 ноября 1630 г., на 59-м году жизни, он скончался. На могиле Кеплера был установлен камень с надписью, заканчивавшейся его словами:

«Я небеса измерял; ныне тени Земли измеряю.
Дух на небе мой жил; здесь же тень тела лежит».

Но вскоре, за годы Тридцатилетней войны (1618—1648), кладбище было разрушено, никаких следов не осталось и от могилы Кеплера. Несчастья преследовали его и после смерти... Его жена и четверо маленьких детей (старшей дочери было девять лет, а самой младшей — семь месяцев) остались без каких бы то ни было средств к существованию. Заботы о них взял на себя зять Кеплера (муж Сусанны, дочери от первого брака) Якоб Барч. Но тот три года спустя умер от чумы. В 1634 г. умерли сыновья Кеплера — 10-летний Гильдеберт и 12-летний Фридмар, а в 1636 г. и их мать. Судьба дочерей Кеплера Кордулы и Анны Марии неизвестна.

Такова печальная и трудная жизнь Кеплера и его близких, Кеплера, который в сочинении «О себе» писал так: «Даже непродолжительное время, проведенное без пользы, причиняет ему страдание..., он непрестанно испытывает раскаяние по поводу упущенного времени», и «то, к чему он стремится, прекрасно, и в большинстве случаев ему удавалось постичь истину».

Перелистаем же еще раз страницы жизни неутомимого труженика и великого законодатели неба...

«Космический кубок» Кеплера. На протяжении первого года пребывании и Граце Кеплер потратил много времени на осмысливание таких проблем: почему планет всего шесть и почему расстоянии между ними именно такие, какие установил Коперник, а не другие? Говоря словами Ю.А. Белого, «будучи уверенным в существовании мудрого промысла божьего, он думает, что при сотворении мира бог должен был исходить из простых числовых свойств и соотношений, использовать совершенные геометрические формы».

В «Предвестнике космографических исследований» Кеплер и стремится дать ответы на указанные выше вопросы. В предисловии он пишет: «Я затратил много времени на эту задачу, на эту игру с числами, но не смог найти никакого порядка ни в численных соотношениях, ни в отклонениях от них». Но, как писал он далее, ему случайно удалось обнаружить, что радиус окружности, описанной вокруг равностороннего треугольника, вдвое больше радиуса окружности, вписанной в этот треугольник. И здесь Кеплера озарила мысль: ведь примерно таково же соотношение между радиусами круговых орбит Сатурна и Юпитера (по Копернику r_S : r_J = 8,2 : 5,2). Но, вписывая между орбитами Юпитера и Марса квадрат, между орбитами Марса и Земли — пятиугольник и т. д., Кеплер убедился, что здесь расхождения с данными Коперника еще больше.

«И вот я снова устремился вперед. Зачем рассматривать фигуры двух измерений для пригонки орбит в пространстве? Следует рассмотреть формы трех измерений, и вот, дорогой читатель, теперь мое открытие в Ваших руках!».

Как известно (и об этом знали уже древние греки), в пространстве трех измерений может быть лишь пять правильных выпуклых многогранников, у которых все грани являются правильными и равными между собой многоугольниками и все двугранные углы которых равны между собой. Это тетраэдр (четыре треугольные грани — правильная пирамида с равносторонним треугольным основанием), куб или гексаэдр (шесть граней-квадратов), октаэдр (восьмигранник, грани которого — равносторонние треугольники), додекаэдр (двенадцатигранник с гранями в виде равносторонних пятиугольников) и икосаэдр (двадцатигранник, грани которого — равносторонние треугольники). Поверхность описанного шара (сферы) проходит через вершины такого многогранника, а поверхность вписанного касается центра каждой грани, причем центры обеих сфер совпадают.

Так вот почему, «догадался» Кеплер, планет лишь шесть! Ведь в природе могут существовать всего лишь пять правильных выпуклых многогранников! И он устанавливает между орбитами планет по одному многограннику: между Сатурном и Юпитером куб, между Юпитером и Марсом тетраэдр, между Марсом и Землей додекаэдр, между Землей и Венерой икосаэдр, между Венерой и Меркурием октаэдр. Дальше Кеплер рассчитывает радиусы вписанных и описанных сфер, которые оказались довольно близкими к установленным Коперником расстояниям планет от Солнца.

Чтобы устранить расхождение своих результатов с данными Коперника, Кеплер допустил, что каждая из планетных сфер имеет определенную «толщину». Здесь же он говорит: «Аналогично как источник света размещен в Солнце, сама первопричина движения также находится в том месте, которое занимает Солнце, причем, несомненно, в его центре, и, таким образом, Солнце одновременно является вместилищем жизни, движения и световой души».

Как отмечает Ю.А. Белый, уже во введении и первой главе Кеплер проявляет себя как восторженный сторонник учения Коперника, а «Космографическая тайна» была первым недвусмысленным публичным выступлением профессионального астронома в защиту коперниканства, началом его триумфального распространения. Огромное значение имело и то обстоятельство, что в приложении к книге Кеплер поместил «Первое повествование о книгах вращений Николая Коперника» Ретика, которое во времена Кеплера уже было редкостью. Тем самым уже первая книга Кеплера сыграла важную роль в пропаганде гелиоцентрического мировоззрения. А ведь очень многие ученые в то время были крайне осторожными! Так, Галилео Галилей, получив от Кеплера «Космографическую тайну», написал ему в ответ, что не решается публиковать имевшиеся в то время у него доказательства правильности учения Коперника, «чтобы не вызвать потока насмешек над нашим учителем». Кеплер тут же продемонстрировал ему свою решительность: «Решайтесь, выступим одновременно. Дружными усилиями мы сдвинем этот экипаж. Своими доказательствами Вы поможете тем из наших сторонников, которые теперь еще придерживаются неправильных суждений. Я думаю, что очень немногие из знаменитых математиков Европы будут против нас, так как могущество истины велико». Увы, кроме математиков, в Европе были еще и философы, были и теологи, многие из которых думали так же, как и Маттиас Гафенреффер, главный теолог и ректор Тюбингенского университета. Это он настойчиво предостерегал Кеплера не помещать в свою книгу главу о совместимости коперниканской системы с Библией; следует, мол, «выступать при изложении подобных гипотез лишь в качестве чистого математика, который не должен беспокоиться, соответствуют ли эти учения сотворенным вещам или нет». И далее едва ли не главный аргумент: «Ни с чем, однако, не сообразно, чтобы действительность незамедлительно приспособлялась к придуманным каждым магистром гипотезам»...

Кеплер, однако, смело пошел вперед...

«Новая астрономия». После публикации «Космографической тайны» Кеплер продолжал поиски числовых соотношений, которыми описывается движение планет вокруг Солнца, надеясь установить связь между ними и законами музыкальной гармонии пифагорейцев. Он понимал, что для успеха ему нужны данные многолетних наблюдений планет, и знал, что единственным в мире человеком, который располагал такими данными, был Тихо Браге. В письме Мёстлину Кеплер писал: «Пусть все хранят тишину и прислушиваются к Тихо, который посвятил 35 лет жизни своей обсерватории... Я жду только Тихо. Он растолкует мне порядок и размещение орбит. Тогда надеюсь, если Бог продлит мне жизнь, что однажды я сооружу чудесное здание». И далее: «Тихо... обладает несметными сокровищами, но он не знает, как их следует употреблять, как это бывает у очень богатых людей. Следовательно, кто-то должен попытаться силой вырвать эти богатства у него».

Стечением обстоятельств Браге в поисках пристанища оказался в Праге, такая же трудная судьба привела к нему Кеплера. Так, скажем его словами, материал для возведения нового здания попал в руки умелого архитектора, который и использовал все это для своего замысла...

Но сначала несколько слов о крупном вкладе Кеплера в исследование законов геометрической и физиологической оптики, изложенном им в двух его фундаментальных книгах — «Дополнения к Виттелию, в которых излагается оптическая часть астрономии» (1604 г.) и «Диоптрика, или доказательство того, как становится видимым изображение с помощью недавно изобретенной зрительной трубы» (1611 г.). В первой книге Кеплер, в частности, доказал, что интенсивность света обратно пропорциональна квадрату расстояния от источника света, указал на существование солнечной короны (как протяженной атмосферы Солнца; впрочем, само явление короны, наблюдающееся при затмении, по его мнению, могло быть и результатом наличия атмосферы у Луны). Кеплер открыл явление полного внутреннего отражения, описал анатомическое строение глаза, действие очковых линз и за несколько лет до построения первых телескопов дал их математическое обоснование. В «Диоптрике» он предложил при построении телескопов использовать комбинацию двух двояковыпуклых линз. Тем самым значительно увеличивалось поле зрения, причем в отличие от телескопа Галилея (см. начало раздела «А все-таки она движется!») по всему полю зрения объекты были видны одинаково ясно и четко (рис. 43). Первый телескоп такой системы был построен Христофором Шейнером (1575—1650), немецким математиком и астрономом, уже в 1613 г., а к 1640 г. «кеплерова труба» вытеснила все прежние системы телескопов.

Рис. 43. Схемы телескопов Галилея (а) и Кеплера (б)

В 1609 г. была опубликована «Новая астрономия, причинно обоснованная; или физика неба, изложенная в исследованиях движения планеты Марс по наблюдениям благороднейшего мужа Тихо Браге». В ней Кеплер дал вывод первых двух законов движения планет, названных впоследствии его именем. В современной формулировке они звучат так:

I. Все планеты движутся по эллипсам, в одном из фокусов которых (общем для всех планет) находится Солнце.

II. Площади, описываемые радиусами-векторами планет, пропорциональны времени.

В предисловии к «Новой астрономии» Кеплер объяснил, почему он в своей книге решил подробно рассказать об успехах и неудачах, которые сопровождали его в работе: «Для меня важно не просто сообщить читателю, что я должен сказать, но прежде всего ознакомить его с доводами, оговорками, счастливо преодоленными опасностями, которые привели меня к моим открытиям. Когда Христофор Колумб, Магеллан и португальцы... повествуют, как они сбивались с пути и блуждали в своих путешествиях, мы не только прощаем им это, но, более того, мы не желаем пропуска этих рассказов, так как тогда при чтении было бы потеряно впечатление о всем значительном в их предприятиях. Пусть же поэтому и мне не поставят в вину, когда я, вызывая у читателя интерес, пойду подобным путем в своем изложении». И дальше шаг за шагом Кеплер показывает, как он начинал свои вычисления, применял эпициклы, и в итоге пришел к установлению законов движения планет.

Кеплер четко осознавал: «Только Марс предоставляет нам возможность проникнуть в тайны астрономии, которые иначе оставались бы навсегда скрытыми от нас». Однако, упоминая предыдущих исследователей, он отмечает, что «Марс смеялся над их ухищрениями, расстраивал их замыслы и безжалостно разрушал их надежды... Древние жаловались на это не один раз, а неутомимый исследователь тайн природы, знаменитейший из латинян Плиний объявил борьбу с Марсом непосильною для смертных».

Приступая к работе, Кеплер четко представлял себе, что движение планет происходит вследствие воздействия на них некоей силы, исходящей от Солнца. Поэтому плоскости планетных орбит должны проходить через центр Солнца (Коперник же полагал, что плоскость орбиты Марса колеблется в пространстве, хотя, конечно, физической причины этого явления указать не мог). А, главное, если движением планеты управляет Солнце, то его сила действует на планету более интенсивно, когда она находится ближе к источнику, и наоборот. Таким образом, скорость планеты будет различной в зависимости от расстояния до Солнца.

Полагая орбиту Марса круговой, Кеплер (в соответствии с представлениями Птолемея об эксцентре и «уравнивающей» точке) поставил перед собой задачу найти: 1) радиус орбиты, 2) расстояние Солнца от центра орбиты, 3) расстояние «уравнивающей точки» (экванта) от центра орбиты (Кеплер решил проверить правильность утверждения Птолемея, что расстояния между центром орбиты и эквантом и от центра орбиты до Солнца одинаковы), а также 4) направление линии апсид по отношению к неподвижным звездам. Для определения четырех неизвестных величин были взяты данные Тихо Браге о четырех противостояниях Марса: в 1587, 1591, 1593 и 1595 гг. Решение находилось методом последовательных приближений, выполненных Кеплером на 900 листах мелким почерком...

В результате утомительных вычислений Кеплер установил, что полный эксцентриситет орбиты Марса равен 0,18564 долям радиуса, причем Солнце отстоит от центра на 0,11332, а эквант — на 0,07232 доли радиуса. Рассчитывая на этой основе положения Марса для других противостояний, Кеплер получил расхождения, меньшие 2′. Это была точность наблюдений Тихо, погрешность которых была так велика из-за значительного диаметра Марса, неудовлетворительного знания параллакса и рефракции. Казалось бы — все хорошо!

Однако как только Кеплер начал вычислять промежуточные положения Марса и сопоставлять их с наблюдениями, то обнаружил, что расхождения достигают 8′. Чтобы по достоинству оценить эту величину, вспомним, что точность наблюдений во времена от Птолемея до Коперника не была выше 10′, а поэтому оба создателя систем мира могли бы этим расхождением вообще пренебречь. Но Кеплер пишет, что «нам же, благодаря милосердию божию, дан в лице Тихо Браге такой добросовестный наблюдатель, что в его наблюдениях ошибка в 8′, характерная для птолемеева вычисления, попадается лишь для того, чтобы мы с благодарностью оценили эту милость и воспользовались ею. Наконец, это затруднение дает нам возможность найти истинный вид небесных движений... Таким образом, эти 8′ указали путь к обновлению всей астрономии, они явились материалом для большей части данной работы». В итоге «здание, которое мы возвели на фундаменте наблюдений Тихо, мы снова разрушили... Это было нам наказанием за следование таким правдоподобным, но в действительности ложным аксиомам великих авторитетов прошлого»...

После этого Кеплер решил отказаться от представления о том, что орбитой Марса является окружность, и решил прежде всего исследовать орбиту самой Земли, на которой находится наблюдатель. Но как это сделать? Где взять ориентир, который дал бы возможность определять положение Земли относительно Солнца?

Решение Кеплера было гениально простым: этим ориентиром будет сам Марс! Ведь через каждые 687 суток (= T — сидерическому периоду обращения планеты) он возвращается в ту же самую точку своей орбиты, через каждые 687 суток его расстояние от Солнца (независимо от того, какой является его орбита!) будет таким же. Что же касается Земли, то за эти 687 суток ей не хватит 43,5 суток для того, чтобы осуществить два полных оборота вокруг Солнца. Поэтому, если в начальный момент t₀ Солнце, Земля и Марс находились на одной прямой, то к моменту t₀ + T Земля отстанет от Марса на угол α₁ ≈ 43°, к моменту времени t + 2T — на угол α₂ ≈ 86° и т. д. (рис. 44). Точное значение угла α_n можно установить после того как будет измерено угловое расстояние Марса от Солнца в момент t₀ + nT. Так задача была сведена к решению треугольников «Земля — Солнце — Марс», в которых расстояние Солнце — Марс одинаково. Сопоставляя вычисленные углы α_n с наблюдениями, Кеплер определил, что эксцентриситет земной орбиты равен 0,01837 и что Земля движется по ней быстрее тогда, когда она ближе к Солнцу (в перигелии). А это, в свою очередь, дало возможность более тщательно исследовать и орбиту Марса. Кеплер установил, что наибольшее расстояние Марса от Солнца (в радиусах земной орбиты) равно 1,6678, а наименьшее 1,3850. Поскольку же при этом среднее расстояние планеты от Солнца равно 1,5264, отсюда следует, что эксцентриситет орбиты Марса равен 0,0926, т. е. он ровно вдвое меньше найденного раньше расстояния «Солнце — эквант».

Рис. 44. К определению Кеплером эксцентриситета земной орбиты

Далее, сопоставляя значения скорости движения Земли в афелии и перигелии, Кеплер пришел к выводу, что эта скорость обратно пропорциональна расстоянию Земли от Солнца. Он предположил, что это справедливо при любом положении Земли на ее орбите, для любого момента времени t, и составил формулы, по которым можно было рассчитать положение Земли на ее орбите в различные моменты времени.

После этого Кеплер разделил орбиту Земли на 360 частей так, что моментам времени t₁, t₂, t₃, ... , t_n, ... ,t₃₆₀ соответствовали положения Земли на орбите T₁, T₂, T₃, ... , T_n, ... ,T₃₆₀. При этом время, необходимое для прохождения планетой определенного отрезка дуги ее орбиты, обратно пропорционально скорости и прямо пропорционально расстоянию планеты от Солнца. Поэтому, чтобы определить время, на протяжении которого планета описывает большую дугу, следует сложить все промежуточные расстояния «планета — Солнце». Так Кеплер нашел, что t_m − t_i ∼ a_i + a_k + a_l + a_m, где a_i — упомянутое расстояние в момент времени t_i. Оказалось, что эта зависимость не зависит от того, на каком участке орбиты производится сравнение. Иначе говоря, эта сумма постоянна, одна и та же для всех участков орбиты, пройденных планетой за одинаковые промежутки времени.

Вспомнив далее, как Архимед, определяя площадь круга, разбивал его на бесконечно большое число треугольников, Кеплер переходит от суммы расстояний к площади сектора, описанной радиус-вектором планеты. «Следовательно, — пишет он, — площадь, описываемая отрезком Солнце — планета, является мерой времени, необходимого для прохождения планетой соответственной дуги орбиты». Это и есть второй закон Кеплера, открытый им раньше первого.

Одного этого закона, однако, оказалось недостаточно для того, чтобы делать прогнозы будущих положений планеты на орбите. Необходимо было установить еще и форму самой орбиты. И Кеплер снова погружается в вычисления. Из них следовало, что в точках между афелием и перигелием Марс находится ближе к Солнцу, чем это могло быть в случае круговой орбиты.

Какова же все-таки эта орбита? Овал? Или овоид (замкнутая яйцевидная кривая)? В лихорадочных поисках Кеплер отбрасывает один вариант за другим. По его словам, «раздумывая и размышляя, я чуть не сошел с ума». И вот: «Правда лежит между окружностью и овалом, как будто орбита Марса есть точный эллипс». Но, поместив Солнце в центре эллипса, он пришел к выводу, что это противоречит установленному им закону площадей.

Продолжая поиск, Кеплер наконец заметил, что боковая сплюснутость орбиты — разность между радиусом окружности и меньшей полуосью овала — равна 0,00429. А это точно равно половине квадрата эксцентриситета, определенного им ранее (0,0926² = 0,00857). Но именно такими и должны быть соотношения для эллипса (если a и b — соответственно большая и малая полуоси, то b = a√(1 − e²) и при e ≪ 1 имеем b = a(1 − e²)^½ ≈ a(1 − ½e²), а также (a − b)/a ≈ ½e². Еще вычисления — и орбита планеты найдена!

Кеплер делает вывод, что Солнце находится не в центре, а в фокусе эллиптической орбиты, по которой движется планета. Так он, «не прекращая ощупывать все места окружающей тьмы, вышел, наконец, на яркий свет истины»...

Одновременно Кеплер установил, что орбита Марса наклонена к плоскости эклиптики под углом 1°50′. В 1614 г. он проверяет справедливость найденных им законов движения планет для Венеры, а через год и для Меркурия. В результате не менее изнурительных расчетов он определил параметры орбит для всех известных тогда планет.

«Гармония мира». В 1619 г. вышла из печати книга Кеплера «Гармонии Мира пять книг», в которой был выведен третий его закон. Сначала в ней речь идет о правильных многоугольниках, т. е. о «Правильных фигурах, производящих гармонические пропорции», о «Конгруэнции гармонических фигур», о «Происхождении гармонических пропорций». Пятая же часть книги имеет название «Совершеннейшая гармония в небесных движениях и касающееся ее происхождение эксцентриситетов, радиусов орбит и времен обращения». Начинается она словами:

«То, что я предположил уже 22 года назад еще до того, как я нашел пять основных систем небесных орбит; в чем я сам полностью был убежден еще до того, как прочитал «Гармонию» Птолемея; о чем я писал своим друзьям еще до того, как получил полную уверенность в своей правоте; о чем 16 лет назад я писал как об исследуемой проблеме; чему я посвятил значительную часть своей жизни путем проведения астрономических исследований, что заставило меня разыскать Тихо Браге и избрать местом жительства Прагу, — то я, наконец, осуществил, и мне удалось сформулировать это лучше, чем я когда-либо надеялся. Этим я нашел наличие гармонии как в связях, так и в частностях. Свою задачу я осуществил не тем путем, который казался мне правильным, а совершенно отличным путем, чрезвычайно совершенным и для этого дела пригодным».

И дальше: «До сих пор мы говорили о различных промежутках времени и [проходимых за это время] дугах для одной и той же планеты. Теперь же должна пойти речь о движениях двух планет, сравниваемых друг с другом. Итак, здесь предстоит довершить и ввести сюда некоторую часть моей «Космографической тайны», оставленную нерешенной 22 года тому назад, так как тогда дело еще не было ясно для меня. И вот, после того, как непрерывным трудом весьма долгого времени были из наблюдений Браге найдены верные промежутки орбит, наконец-то, наконец-то, подлинная пропорция между периодами и размерами орбит

... хоть и поздно, заметила бездейственного,
заметила все-таки и пришла после продолжительного времени...

...она наконец победила слепоту моего ума; это было столь великой наградой и моей семнадцатилетней работы над наблюдением Браге, и направленного согласно с нею размышления, что я сперва готов был думать, будто сплю и предвосхищаю искомое среди данных. Но в высшей степени верно и точно, что отношение между периодами обращения каких-нибудь двух планет как раз равняется полуторной степени отношения их средних расстояний, т. е. радиусов орбит...».

Сегодня для нас более привычна такая формулировка этого закона:

III. Квадраты сидерических периодов обращения планет вокруг Солнца относятся между собой, как кубы их средних расстояний от него.

«Очерки коперниканской астрономии». Тремя частями, в 1618, 1620 и 1621 гг. (всего около 1000 страниц текста), вышла книга Кеплера «Epitomae Astronomiae Copernicanae», т. е. «Очерки (точнее — сокращения) коперниканской астрономии». Это был первый учебник по астрономии, написанный в форме вопросов и ответов, который основывался на совершенно новых принципах. В «Очерках» центральное место в планетной системе заняло Солнце, планеты же обращаются вокруг него по эллиптическим орбитам. Здесь, «наш мир с его Солнцем является одним из неисчислимых миров». Млечный Путь — это кольцо звезд, вблизи плоскости которого расположено Солнце с планетами. Законы движения планет используются для описания обращения Луны вокруг Земли. Кеплер также применяет свой третий закон при описании недавно открытых Галилеем четырех спутников Юпитера.

В «Очерках» Кеплер произвел переоценку расстояния от Земли до Солнца, которое на протяжении 1800 лет, со времен Гиппарха принималось равным 1200 радиусам Земли. Ход рассуждений Кеплера был таков: если указанное расстояние правильно, то суточный параллакс Солнца должен составлять около 3′. Марс же в противостояниях бывает в 2,5 раза ближе, чем Солнце, поэтому и его параллакс должен быть соответственно больше. Но никакого параллакса у Марса Кеплеру измерить не удалось. Отсюда следовало, что и Марс, и Солнце находятся от Земли значительно дальше. И здесь Кеплер исходил из представлений о гармонии, присущей Солнечной системе: дескать, если Земля представляет собой убежище измеряющих существ, то есть основание ожидать, что размеры Солнечной системы находятся в некотором простом соотношении с размерами Земли. Кеплер принял, что объем Солнца во столько раз больше объема Земли, во сколько раз его расстояние превосходит земной радиус. Полученное Кеплером значение астрономической единицы было более близким к истинному значению, чем предыдущие оценки, но все же примерно в семь раз меньше его. Кеплер принимал, что параллакс Солнца равен 0′59″, а параллакс Луны 58′21″. Следовательно, расстояние до Солнца в 59 раз больше, чем до Луны, а та, в свою очередь, «в апогее удалена от Земли примерно на 59 земных радиусов». Кеплер принимает, что 1° дуги большего круга равен 15 германским милям, тогда полная дуга большого круга на поверхности Земли равна 5400 милям, радиус Земли — 860 милям и расстояние до Луны — 50 740 милям = 376 490,8 км (1 германская миля= 7,42 км).

Далее Кеплер «априори вывел», что «радиус Солнца относится к радиусу сферы Сатурна так же, как последний — к радиусу сферы неподвижных звезд. Если это предположение верно, то радиус сферы Сатурна составляет лишь 1/2000 радиуса сферы неподвижных звезд, радиус сферы, содержащей Землю и Луну, достигает едва 1/20 000 радиуса сферы неподвижных звезд», а «радиус лунной сферы равен 1/59 радиуса сферы, содержащей Землю и Луну». Следовательно, расстояние от Земли до неподвижных звезд по Кеплеру равно 20 000 астрономических единиц или примерно 70 млн радиусов Земли.

В «Очерках» Кеплер подробно изложил теорию солнечных и лунных затмений. Явление приливов он объяснил притяжением Луны. Кеплер поставил также вопрос о физической причине планетных движений, повторяя высказанные ранее в «Новой астрономии» взгляды, что тяготение является свойством всех тел одинакового типа. Планеты как бы разделяют с Солнцем его собственное вращение. От Солнца до планет простирается определенная «движущая сила», подобная лучам света и тепла, которая и втягивает планету в движение вокруг Солнца. «Действует конфликт между движущей силой Солнца и бессилием или материальной несуразностью (инерцией) планеты. Оба эти начала в определенном отношении одерживают победу, ибо первое сдвигает планету с ее места, а второе частично освобождает тело планеты от связывающих ее оков..., но лишь до того момента, когда она снова подхватывается этой вращающей силой». Действие же «движущей души» Солнца направлено не вдоль прямой «Солнце — планета», а перпендикулярно ей. Чтобы объяснить движение планет по эллиптическим орбитам, Кеплер считал, что все планеты являются магнитами, силы которых, то отталкивающие, то притягивающие, складываются с действием Солнца (рис. 45).

В 1627 г. вышли из печати «Рудольфинские таблицы», которые на протяжении почти 100 лет использовались для предвычислений положений Солнца, Луны и планет и были настольной книгой астрономов и мореплавателей. В ней приводился также каталог 1005 звезд, в основу которого был положен каталог из 777 звезд, составленный Тихо Браге, таблицы рефракции, географические координаты крупнейших городов мира.

Рис. 45. Представление Кеплера о действии на планету силы со стороны Солнца (рисунок из книги «Очерки копер ни канской астрономии»)

Уже после смерти Кеплера, в 1634 г., было опубликовано его научно-фантастическое произведение «Сон, или посмертное сочинение о лунной астрономии» — первое в истории астрономии сочинение, в котором явления описываются так, как их наблюдатель увидел бы, находясь на Луне. Как отметил Кеплер в Примечании к этой книге, «цель моего «Сна» состоит в том, чтобы на примере Луны привести доводы в пользу движения Земли». Примечания (а они занимают большую часть книги) составлены после 1620 г., когда учение Коперника уже подвергалось гонениям. И еще раз выступив в его защиту, Кеплер писал: «По отношению к труду Коперника основная несправедливость исходит от людей, не сведущих в астрономии... Они полагают, будто книгу Коперника нельзя читать, не исключив из нее прежде движение Земли. Разделять подобное мнение — все равно что утверждать, будто книгу Коперника нельзя читать, не предав ее сначала огню...».

Конкретным действием в защиту гелиоцентрической модели мира Коперника и была публикация Кеплером его «Очерков коперниканской астрономии», этой, по словам А. Берри, «одной из увлекательнейших книг Кеплера, так как она свободна от странностей, обычно делающих столь утомительным чтение его произведений». Отметим еще, что, говоря в «Очерках» о суточном вращении Земли, Кеплер в доказательство приводит утверждение, что «природа в достижении своей цели всегда использует простейший путь». Такими простейшими путями для планет оказались эллиптические орбиты вместо сложной паутины эпициклов...

Кеплер выступил за освобождение астрономии от засилия теологии: «В теологии имеет значение авторитет, в философии — разумные доводы. Ведь был святым Лактанций, отрицавший шарообразность Земли, святым был и Августин, признавший шарообразность Земли, но отрицавший существование антиподов, свят и официум наших дней, признающий, что Земля невелика по размерам, но отрицающий ее движение. Для меня же святее всего истина, когда я при всем моем глубоком уважении к отцам церкви доказываю с помощью философских рассуждений, что Земля имеет форму шара, населена со всех сторон антиподами и занимает среди звезд совсем незаметное и незначительное место»². Стоит ли удивляться, что «Очерки» уже в 1619 г. были внесены в «Индекс запрещенных книг», из которого были исключены лишь в 1835 г....

Девизом Кеплера было «Бездеятельность — смерть для философии: так будем же жить и трудиться». И разве это не закономерно, что Карл Маркс назвал его, рядом со Спартаком, своим самым любимым героем?

Примечания

1. Белый Ю.А. Иоганн Кеплер. — М.: Наука, 1971. — С. 19.

2. Рыбка Е., Рыбка П. Коперник: Человек и мысль. — М.: Мир, 1973. — С. 274.