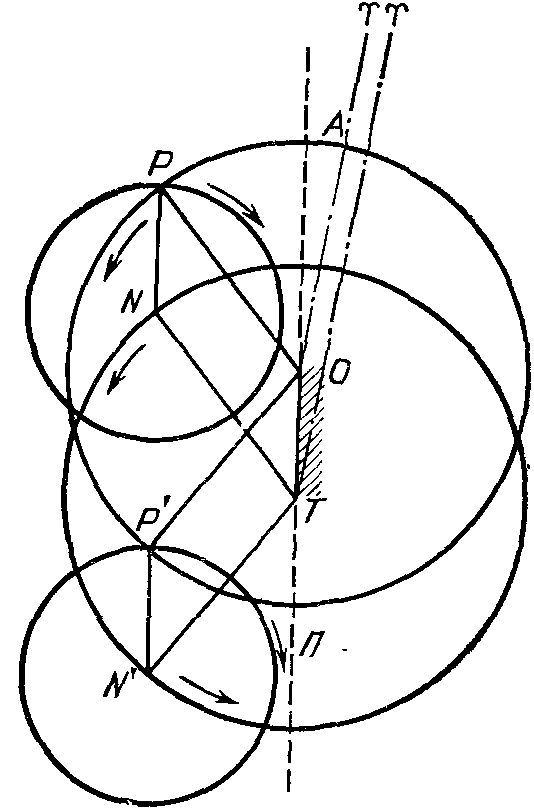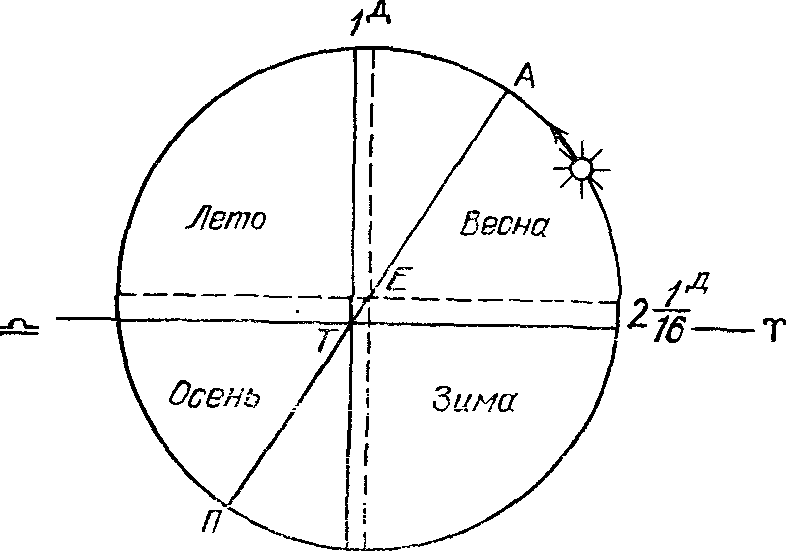
Он заложил фундамент

Как открыть прецессию? Сегодня все единодушны в том, что благодаря трудам древнегреческого астронома Гиппарха (ок. 185—125 гг. до н. э.) астрономия начала оформляться в точную науку. Гиппарх первым начал систематические астрономические наблюдения и их всесторонний математический анализ, он разработал теорию движения Солнца и Луны, метод предсказания (с точностью до одного — двух часов) затмений, заложил основы сферической астрономии и тригонометрии.

О жизни Гиппарха известно очень мало. Родился он в Никее (теперь г. Изник в Турции), некоторое время был и Александрии, а работал на острове Родос, где построил астрономическую обсерваторию.

Прежде всего, Гиппарх установил, что следует различать звёздный год как промежуток времени между двумя последовательными прохождениями Солнца вблизи определенной звезды и тропический год — промежуток времени от одного весеннего равноденствия до другого. Сравнивая момент летнего солнцестояния, наблюдавшегося Аристархом в 280 г. до н. э., со своими наблюдениями в 135 г. до н. э., Гиппарх сделал вывод, что продолжительность тропического года равна 365¼—1/300 суток или 365^д5^ч55^м16^с, т. е. он короче звездного на 20 минут. Это объясняется прецессией — перемещением точки весеннего равноденствия навстречу Солнцу. Открытие прецессии и было важнейшим из всего сделанного Гиппархом.

Естественно, может возникнуть сомнение в том, как могли установить передвижение «невидимой» точки пересечения эклиптики с небесным экватором за год на очень малую величину в те далекие времена... А между тем все решается «очень просто». Достаточно лишь принять во внимание два факта. Во-первых, угловое расстояние Солнца от точки весеннего равноденствия (эклиптическую долготу Солнца) можно установить, измерив его высоту над горизонтом и момент прохождения через меридиан, по которой сама долгота вычисляется путем несложных расчетов или находится по заранее составленным таблицам. Во-вторых, в середине лунного затмения, когда Луна находится на небесной сфере точно напротив Солнца, ее долгота от точки весеннего равноденствия на 180° больше долготы Солнца.

Но ведь очень часто в моменты лунных затмений рядом с Луной оказываются яркие звезды! И достаточно измерить их угловые расстояния от центра диска Луны, чтобы таким образом определить их эклиптические долготы. Измерить и записать! Догадаться, что это со временем будет необходимо другим астрономам в их поисках законов мироздания...

Именно так за 169 лет до наблюдений Гиппарха астрономы Аристилл и Тимохарис зафиксировали положение 18 звезд на небе. И вот, наблюдая «свое» затмение Луны, Гиппарх обнаружил, что «в его время Спика опережала осеннее равноденствие на 6°, а во времена Тимохариса — на 8°». Иначе говоря, перемещаясь навстречу Солнцу, точка осеннего (как и весеннего) равноденствия за 169 лет сместилась в направлении звезды Спика (α Девы) на 2°, т. е. на четыре диаметра диска Луны. Измерения эти были проведены, конечно, с невысокой точностью, так как определены лишь градусы. И все же можно было оценить, что в среднем за год смещение составляет 2°: 169 = 43″.

В действительности же годовая прецессия составляет 50,26″. Поэтому в наше время Спика находится уже далеко позади точки осеннего равноденствия, которая, как мы знаем теперь, перемещается вдоль эклиптики на 1° за каждые 72 года.

Теория движения Солнца. Уже задолго до Гиппарха вавилонские и греческие астрономы и среди них Каллипп обнаружили различную продолжительность времен года Гиппарх получил более точные значения: весна (отсчитанная от перехода Солнца через точку весеннего равноденствия до летнего солнцестояния) продолжается 94½ дня, лето — 92½ дня, что в сумме составляет 187 суток, тогда как между осенним и весенним равноденствиями остается 178¼ дня (истинные значения четырех сезонов года — 94,1, 92,2, 88,6 и 90,4 суток). А это значит, что весной Солнце на небесной сфере движется медленнее, чем в любое другое время года, тогда как осенью быстрее всего.

Рис. 13. Установленное Гиппархом различие в продолжительности сезонов года и найденное им направление линии апсид

Сказанное можно представить графически (рис. 13). Можно говорить, что Солнце движется равномерно по окружности с центром в E, однако Земля T сдвинута в квадрант «осень». По отношению к точке T такая окружность будет эксцентром, понятие о котором ввел еще до Гиппарха Аполлоний Пергский (ок. 262 — ок. 200 гг. до н. э.). Долготы же отсчитываются по другой окружности, центр которой совпадает с T. Ближайшая к Земле точка Π орбиты Солнца (в геоцентрической модели — любой планеты) называется перигеем, наиболее удаленная (A) — апогеем (греч. «пери» — около, «апо» — от). Линия AΠ называется линией апсид (греч. «апсис» — свод, вершина). И, наконец, отношение TE/EA = ε есть эксцентриситет эксцентра, угол же γ TA (он обозначается также Π) есть долгота апогея.

Исходя из продолжительности сезонов, Гиппарх определил основные параметры эксцентр а Солнца — эксцентриситет ε = 1/24 — и долготу апогея Π = 65°30′. После этого он смог составить таблицу, по которой можно было установить положение Солнца на небе на каждый день.

Рис. 14. К объяснению тождественности систем «эксцентр» и «эпицикл — деферент» (при σ⃗ = −ω⃗!)

Гиппарх проанализировал и другую возможность объяснения неравномерного годичного движения Солнца по эклиптике — комбинацией эпицикла (греч. «эпи» — на и «киклос» — круг) и деферента (лат. deferens — несущий). Ее сущность становится понятной, если рассмотреть такую «механическую модель»: вращение параллелограмма вокруг одной из его сторон.

Предположим, что стороны параллелограмма TNPO (рис. 14) являются стержнями, соединенными шарнирно, так что каждая из сторон может поворачиваться по отношению к соседней. Закрепим теперь сторону TO неподвижно на плоскости и, взявшись за вершину N, начнем поворачивать параллелограмм вокруг точки T (не поднимая его над плоскостью рисунка!). Очевидно, что при таком поворачивании противоположные стороны параллелограмма будут оставаться взаимно параллельными, точка P будет описывать окружность относительно вершины O, точка N — относительно T, а, кроме того, точка P будет описывать окружность относительно N. При этом, если параллелограмм как единое целое поворачивается против часовой стрелки, то точка P будет описывать окружность относительно точки N, двигаясь в противоположном направлении, т. е. по часовой стрелке, и за один оборот параллелограмма совершает один оборот вокруг N.

Окружность, которую точка N описывает вокруг T, как раз и принято называть деферентом; окружность, которую описывает точка P в ее относительном движении вокруг N, называется эпициклом; окружность, которую описывает точка P вокруг O, как мы уже знаем, называется эксцентром. Здесь точка T играет роль центра мира, точка P изображает истинное Солнце (далее мы скажем — любую планету), точка N — «среднее солнце» («среднюю планету»). Напомним, что по представлениям древнегреческих философов круговое движение обязательно должно быть равномерным, т. е. все названные точки движутся с постоянной угловой скоростью.

Из рис. 14 следует такой вывод: «Если средняя планета N вращается вокруг центра мира T в прямом направлении (против часовой стрелки) с постоянной угловой скоростью, а планета P вращается в то же самое время с той же угловой скоростью в обратном направлении, то движение планеты P относительно центра T будет таким же, как если бы она вращалась с той же самой скоростью и в прямом направлении по эксцентру, радиус которого равен радиусу деферента, а центр O смещен от центра T на отрезок OT, равный радиусу эпицикла NР». Это так называемая теорема Аполлония Пергского; она была известна Гиппарху, который избрал для объяснения движения Солнца (и Луны) гипотезу эксцентра, «поскольку она достигает цели с помощью лишь одного движения». Однако разработка системы деферент — эпицикл позволила позже Птолемею представить с помощью комбинаций этих окружностей все сложности в движениях планет...

Как отмечалось, Гиппарх определил эксцентриситет эксцентра Солнца е в виде отношения ε = OT/OA = PN/NT, т. е. его можно рассматривать как отношение радиуса эпицикла к радиусу деферента. Упомянутое выше годичное неравномерное движение Солнца по эклиптике (и аналогичное движение Луны и планет) древние астрономы называли «первым неравенством». Как видим, его вполне можно моделировать одним из двух упомянутых здесь способов.

Движение Луны. Здесь прежде всего следует упомянуть о том, что Гиппарх с высокой точностью определил продолжительность синодического месяца. Но сначала — о его предшественниках в этом вопросе.

В 432 г. до н. э. греческий астроном Метон установил, что 19 тропических лет составляют 235 синодических месяцев, и это равно 6940 суткам. Отсюда продолжительность года равна 6940/19 = 365^д6^ч19^м, а продолжительность синодического месяца 6940/235 = 29^д12^ч46^м — на 2^м больше истинного значения. При составлении лунно-солнечного календаря Метон в 19-летнем цикле использовал 125 полных месяцев (по 30 дней) и 110 пустых календарных месяцев (по 29 суток). В итоге и получалось 6940 суток.

Позже Каллипп пришел к выводу, что согласие найденных из расчетов календарных единице их астрономическими прообразами будет лучше, если из четырех метоновых циклов исключить одни сутки, приняв, что 76 лет равны 27 759 суткам. Отсюда длина года равна 365¼ суток, а синодического месяца — 27 759/940 дней = 29^д12^ч44^м25^с, а это всего на 22^с больше истинного значения.

Однако открыв прецессию и установив, что продолжительность тропического года меньше 365,25 суток, Гиппарх внес поправку и в каллиппов лунно-солнечный цикл. Он пришел к выводу, что из четырех каллипповых периодов (4×76= 304 года) следует исключить одни сутки. В этом промежутке времени, следовательно, должно насчитываться 27 759×4−1 = 111 035 дней или 940×4 = 3760 лунных месяцев. Отсюда и следует, что

1 солнечный год = 111 035^д/304 = 365^д5^ч55^м16^с,
1 синодический месяц = 111 035^д/3760 = 29^д12^ч44^м2,5^с.

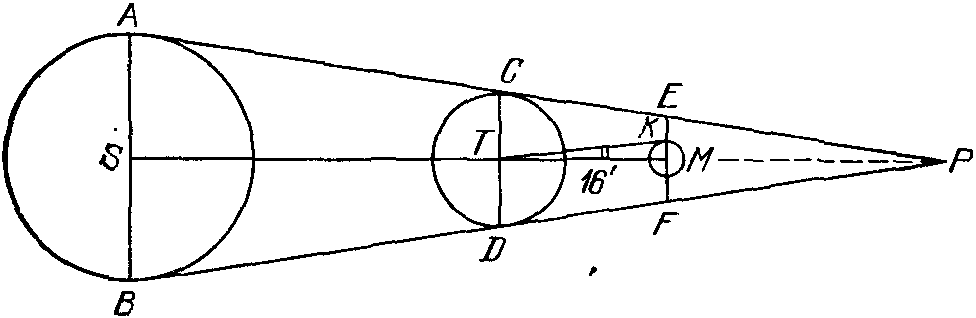
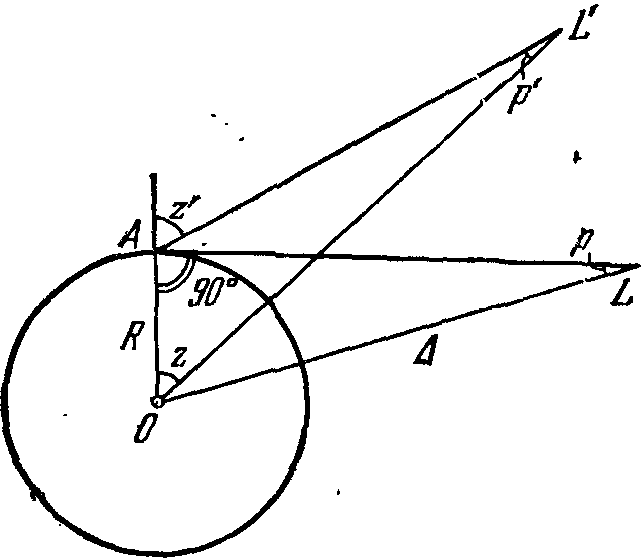
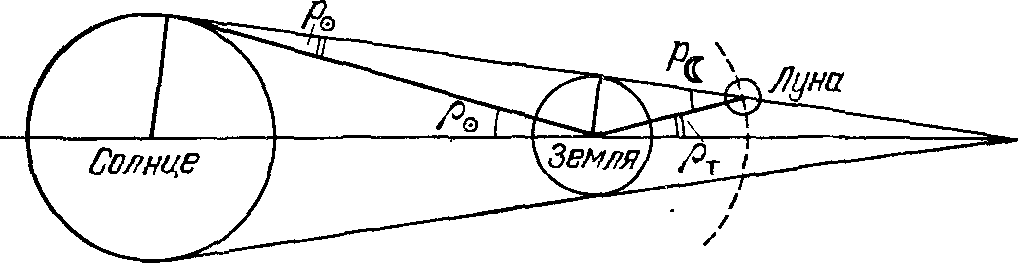
Так было получено значение синодического месяца, всего на 0,3 с меньше его современного значения...

Далее Гиппарх установил, что путь Луны на небесной сфере наклонен к эклиптике под углом 5° и что Луна по своей орбите, с точки зрения земного наблюдателя, движется неравномерно: на протяжении месяца она уходит вперед или отстает от расчетного среднего движения на немногим более 6°! Гиппарх принял, что, как и Солнце, Луна движется по эксцентру, плоскость которого наклонена к эклиптике под углом 5° и который пересекается с нею в двух точках — узлах; тот из них, в котором Луна переходит в северную полусферу относительно эклиптики, называется восходящим узлом, а противоположный — нисходящим. Естественно, что на лунном эксцентре имеется ближайшая к Земле точка — перигей и наиболее удаленная от нее — апогей. Угловая скорость движения Луны в перигее имеет наибольшее значение, а в апогее — наименьшее.

Древние астрономы возвращение Луны в тот уже узел называли «возвращением широты», а возвращение к наибольшей скорости — «возвращением аномалии». На основании наблюдений своих и «древних астрономов» Гиппарх установил, что 126 007 дней + 1 час = 4267 синодическим периодам = 4573 возвращениям аномалии = 4612 обращениям (по отношению к звездам) без 7½°, что почти в точности равно 345 обращениям Солнца. Кроме того, 5458 синодических периодов составляют 5923 возвращения широты. Отсюда, кроме уже приведенного выше (почти с той же точностью) значения синодического месяца, следует и период обращения Луны относительно звезд — 27^д7^ч43^м13,1^с, что всего на 1,7^с больше истинного значения. Так как за 4612 обращений Луна проходит через перигей 4573 раза, т. е. на 39 раз меньше, то Гиппарх сделал вывод, что перигей перемещается в том же направлении, что и Луна, завершая обращение за 8,85 года.

Из приведенных здесь чисел нетрудно получить, что 5458 синодических периодов соответствуют 5899,27 обращения Луны относительно звезд. Как видно, за эти 161 177,96 дня произошло на 23,73 возвращения к широте больше, чем возвращений к той же звезде. Так Гиппарх получил, что узлы лунной орбиты перемещаются навстречу Луне, делая оборот за 6792 суток (истинное значение 6798^д ≈ 18,61 года).

Итак, по Гиппарху, центр эксцентра Луны описывал вокруг Земли круг почти за 9 лет, плоскость же эксцентра, сохраняя наклон к эклиптике, «отступала назад», обеспечивая наблюдаемое движение узлов. Этим было достигнуто многое в описании движения Луны, однако на самом деле оно настолько сложно, что посредством одного эксцентра его представить просто нельзя...

Расстояние и параллакс Луны. Гиппарх пересмотрел задачу об установлении расстояния до Луны и решил ее с высокой для того времени точностью. Сделано это было следующим образом.

Рис. 15. Подобные треугольники, при помощи которых Гиппарх установил расстояние от Земли до Луны

Гиппарху было известно, что угловой радиус Луны составляет 16′, а радиус земной тени на расстоянии Луны 40′(т. е. он в 8/3 раза больше). Последнее можно установить, фиксируя продолжительность полного лунного затмения: Луна перемещается на небе со средней скоростью 0,5° в час, а время ее полного пребывания в тени Земли немногим меньше двух часов. Отсюда следует, что видимый диск Луны укладывается в сечении земной тени почти три раза.

А теперь убедимся в том, что такая серьезная задача, как установление расстояния до Луны, имеет очень простое геометрическое решение. Пусть (рис. 15) точки S, T и M изображают соответственно центры Солнца, Земли и Луны, а FM = R_T— это радиус земной тени на орбите Луны. Поскольку равнобедренные треугольники EFP, CDP и ABP подобны, можно составить такое соотношение:

(DT − FM)/(BS − DT) = TM/ST. (1)

Так как видимые угловые радиусы Луны и Солнца равны, то расстояние до Солнца во столько раз больше, во сколько его радиус R_☉ больше радиуса Луны R_☾. Математически это запишется в таком виде:

ST/TM = R_☉/R_☾ = x. (1.2)

Пользуясь этим соотношением, можно после несложных преобразований записать равенство (1.1) так:

R_☾+ R_T = (1 + 1/x) R_⊕. (1.3)

Как уже указывалось, радиус земной тени R_T = 8/3 R_☾. Поэтому из последнего уравнения следует, что

R_☾ = 3/11 (1 + 1/x) R_⊕. (1.4)

Поскольку величина x значительно превышает единицу (по Аристарху x ≈ 19), вторым слагаемым в скобках можно пренебречь. В итоге находим, что R_☾ ≈ 3/11 R_⊕, а это практически совпадает с современными данными о размерах Луны.

Так как линейный и угловой радиусы Луны известны, то нетрудно определить и само расстояние от Земли до Луны. Действительно, из треугольника TMK имеем

KM/TM = tg 16′, TM = R_☾/tg 16′,

а поскольку tg 16′ = 0,0046, то TM = 218R_☾ или же TM = 59 R_⊕.

Конечно, Гиппарх, закладывавший основы тригонометрии, тригонометрической функции «тангенс» еще не знал, она была введена гораздо позже, но для расстояния от Земли до Луны он получил то же значение 59 R_⊕. Ведь при малых углах α имеем tg α ≈ sin α, а с синусами Гиппарх «умел обращаться»! Отсюда его вывод, сформулированный примерно так: «поскольку угловой радиус Луны равен 16′, то расстояние до нее примерно в 220 раз больше ее радиуса».

Рис. 16. Суточный параллакс светила; параллактическое смещение р тем больше, чем меньше расстояние Δ до светила

Полагают, что Гиппарх, занявшись разработкой метода предвычисления затмений, впервые обратил внимание на необходимость учета параллактического смещения Луны. Суточным параллаксом p называется угол, под которым наблюдатель увидел бы со светила радиус Земли. Когда светило находится на горизонте, этот угол достигает наибольшего значения. Наблюдателю, расположенному в точке A на поверхности Земли, благодаря суточному параллаксу светило кажется ниже, чем это было бы при наблюдениях из центра Земли (рис. 16).

Рис. 17. К определению Гиппархом горизонтального параллакса Луны

У Луны горизонтальный параллакс p_☾ равен 57′. Его величину Гиппарх определил, по-видимому, из таких соображений. В момент, когда при полном лунном затмении в тень Земли входит ровно половина диска Луны (рис. 17), между углами ρ_☉ и ρ_T — угловыми радиусами Солнца и тени Земли на расстоянии лунной орбиты и p_☉ и p_☾ — параллаксами

Солнца и Луны существует зависимость

p_☉ + p_☾ = ρ_☉ + ρ_T.

Так как параллакс Солнца древнегреческие астрономы, и том числе Гиппарх, из-за его малости измерить не могли, то при p_☉ ≈ 0 лунный параллакс приближенно измеряется суммой видимых радиусов Солнца и земной тени. Гиппарх нашел, что После этого нетрудно было определить расстояние до Луны. Приняв p_☾ = 1°, находим

p_☾ = R_⊕/sin 1° = R_⊕/0,0175 ≈ 57 R_⊕,

что практически совпадает с результатом, полученным ранее.

В каталоге — величины звезд. Как сообщает римский писатель Плиний Старший (23—79 гг. н. э.), Гиппарх «открыл новую звезду и другую звезду, которая появилась в то время». По другим данным, он в 134 г. до н. э. заметил вспышку новой звезды в созвездии Скорпиона. Это и натолкнуло Гиппарха на мысль, что в звездном мире, возможно, происходят определенные изменения, которые являются очень медленными, чтобы их можно было обнаружить на протяжении нескольких поколений. Надеясь, что все же это в будущем можно будет установить, он составил каталог звезд, в который вошло 850 объектов. Для каждой звезды была указана ее долгота, измеренная вдоль эклиптики от точки весеннего равноденствия против суточного движения небесной сферы до круга широты, проходящего от полюса эклиптики через звезду, и широта, измеренная от эклиптики вдоль круга широты до звезды¹. Кроме того, была указана звездная величина звезды m (это обозначение, принятое в дальнейшем, — первая буква латинского слова magnitude — величина). Гиппарх разделил звезды на шесть классов таким образом, что самые яркие отнес к первой, а самые слабые — к шестой звездной величине. Кстати, поскольку в то время полагали, что все звезды находятся на одинаковом расстоянии от Земли, то считалось, что чем больше диаметр звезды, тем соответственно она ярче...

Здесь уместно отметить, что именно древние греки выделили на звездном небе отдельные яркие группы звезд — созвездия, которые в основном сохранены и сейчас. Произошло это постепенно. Так, в поэме «Работы и дни» Гесиода упоминаются всего две группы звезд — Плеяды и Орион. Гомер прибавил к ним еще Гиады, Боотеса (Волопаса) и Медведицу. Евдокс, как это видно из стихотворной поэмы Арата «Феномены» (III в. до н. э.), выделил на небе уже 45 созвездий. И вот как указывал Гиппарх ту или другую звезду: «Та, которая на правом плече Персея», «Та, которая на голове Водолея» и т. д....

Французский историк астрономии Жан Батист Деламбр (1749—1822) писал о Гиппархе: «Когда рассмотришь все, изобретенное или усовершенствованное Гиппархом, и поразмыслишь над множеством его трудов и массой содержащихся в них вычислений, то поневоле причислишь его к удивительнейшим мужам древности и назовешь его величайшим из них...». Все здесь истинно, но... единственным сохранившимся сочинением Гиппарха является комментарий к поэме Арата и ее источнику (работе Евдокса). О всех трудах Гиппарха мы знаем из «Альмагеста», в котором Птолемей «на каждом шагу» выражает Гиппарху свое восхищение.

Но как во времена Гиппарха представляли себе эти «изменения в мире звезд»? По крайней мере, один из вариантов этого изложен в трактате Цицерона «О природе богов»: «А природа звезд огненная, поэтому они питаются испарениями земли, моря и прочих вод. Эти испарения вызываются солнцем из согретой земли и из вод. Напившись ими и восстановив себя, звезды и весь эфир изливают их обратно и вновь извлекают их оттуда, так что почти ничего не пропадает, или очень мало, из того, что потребляет огонь звезд и пламя эфира. Из этого следует, по мнению наших, что в конце концов весь мир воспламенится, после того как будет уничтожена вся влага, когда ни земля не сможет питаться, ни воздуху не из чего будет восстановить себя, ведь когда истощится вся вода, то и воздух не сможет образоваться. Итак, ничего не останется, кроме огня. Но от него-то, живого существа и бога, и произойдет восстановление мира, и возродится его красота»²...

Примечания

1. Цицерон. Философские трактаты. — М.: Наука, 1985. — С. 140.

2. Точнее, разделив эклиптику на 12 частей по числу зодиакальных созвездий, древние астрономы указывали «знак зодиака» и долготу светила, отсчитанную от «начала знака».