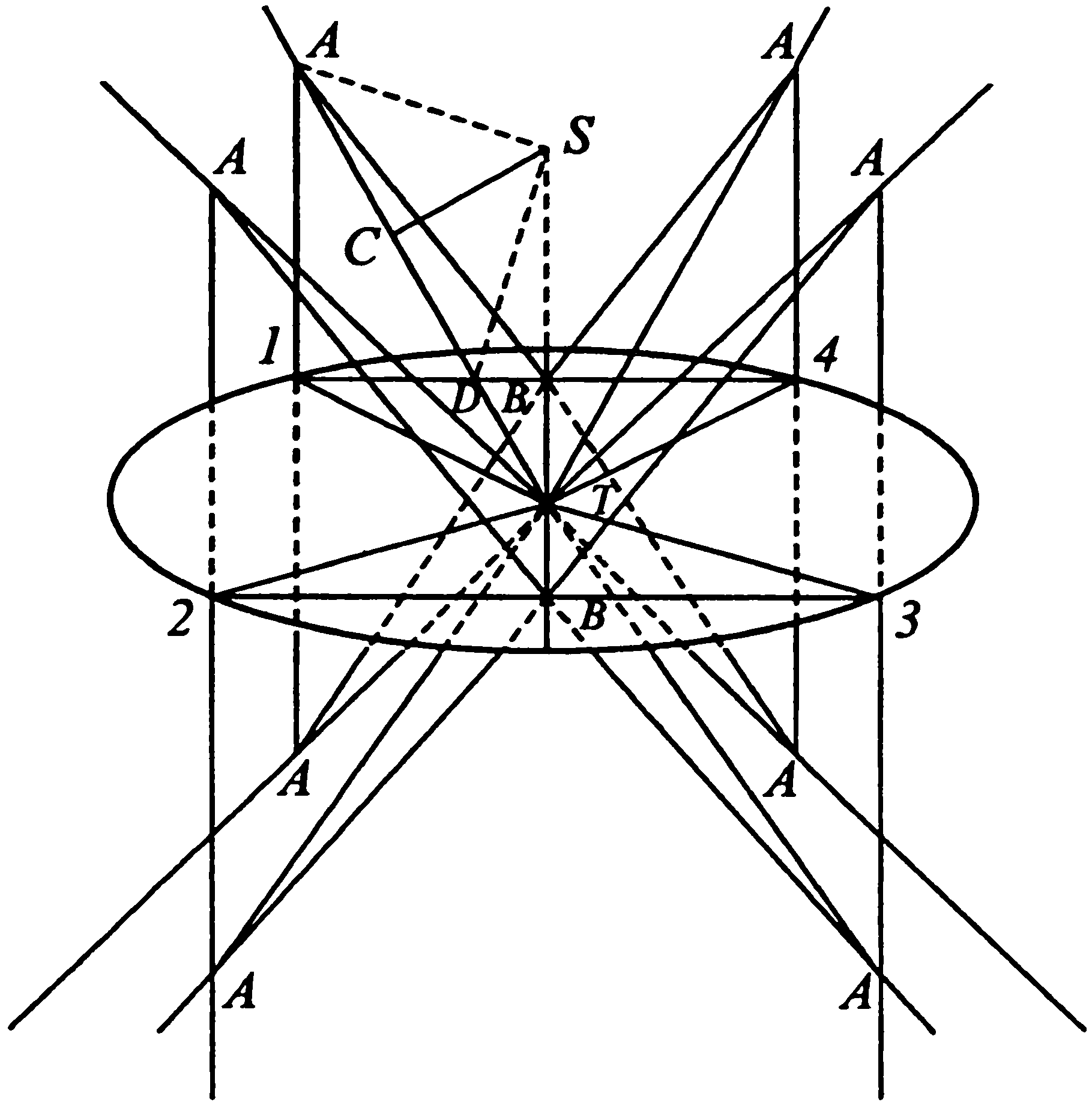
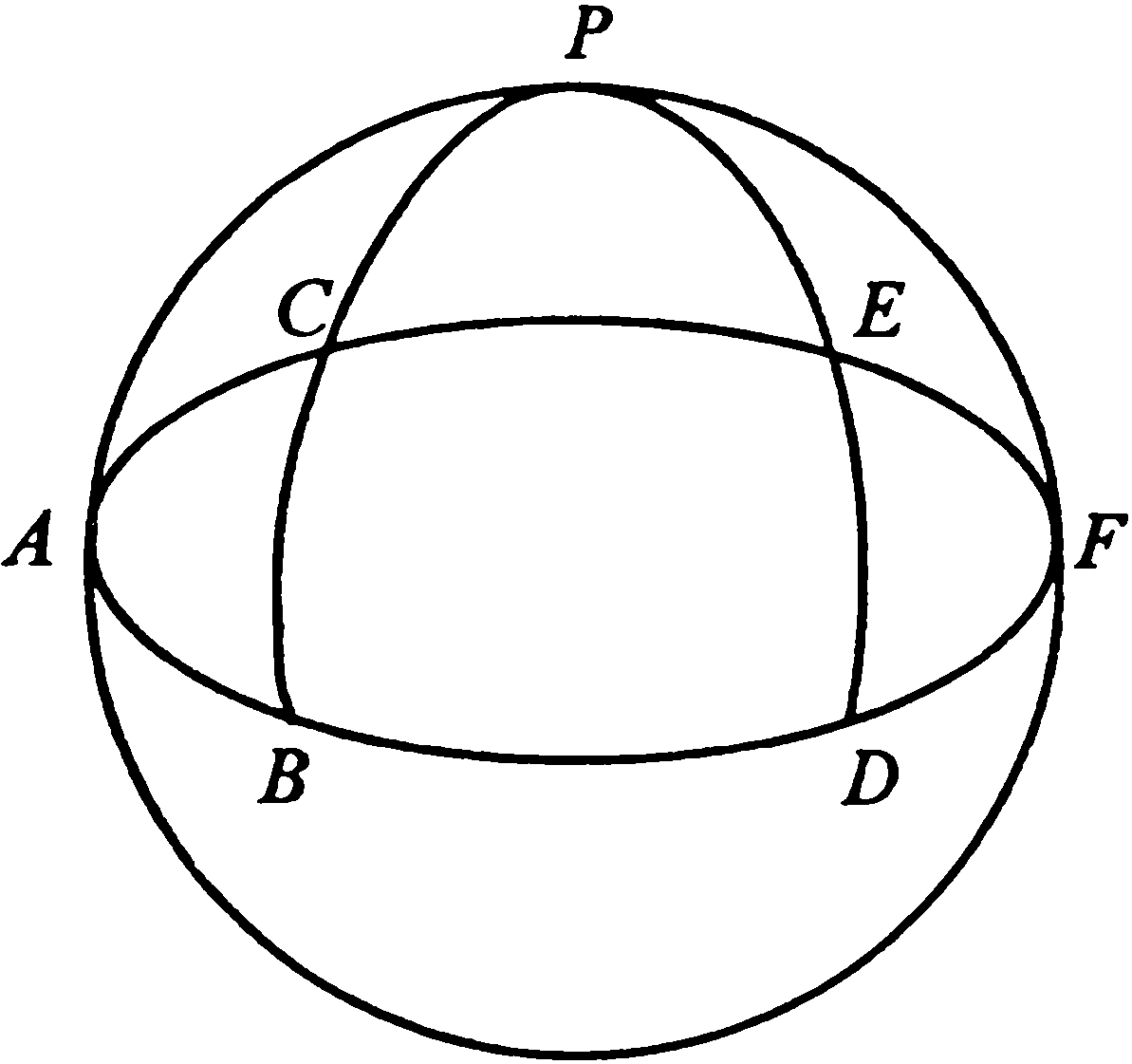
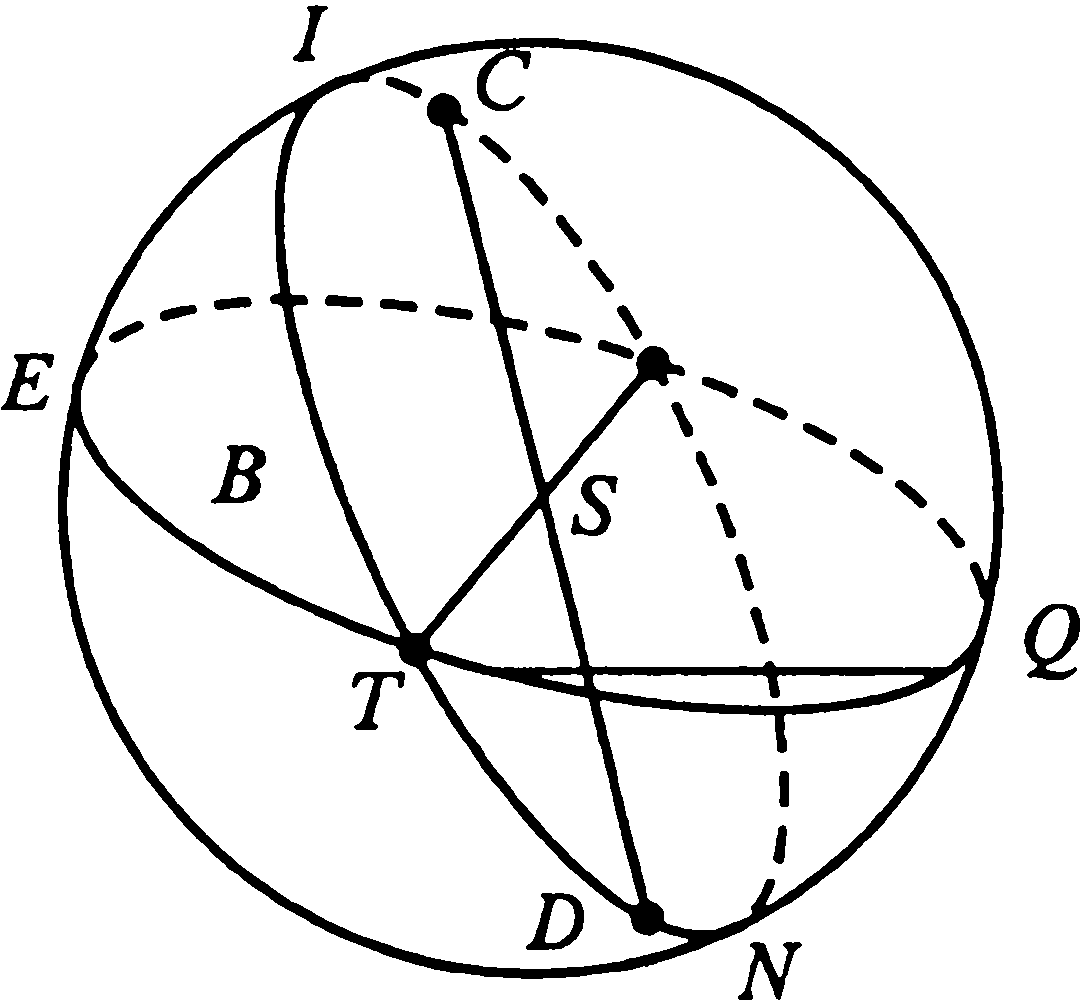
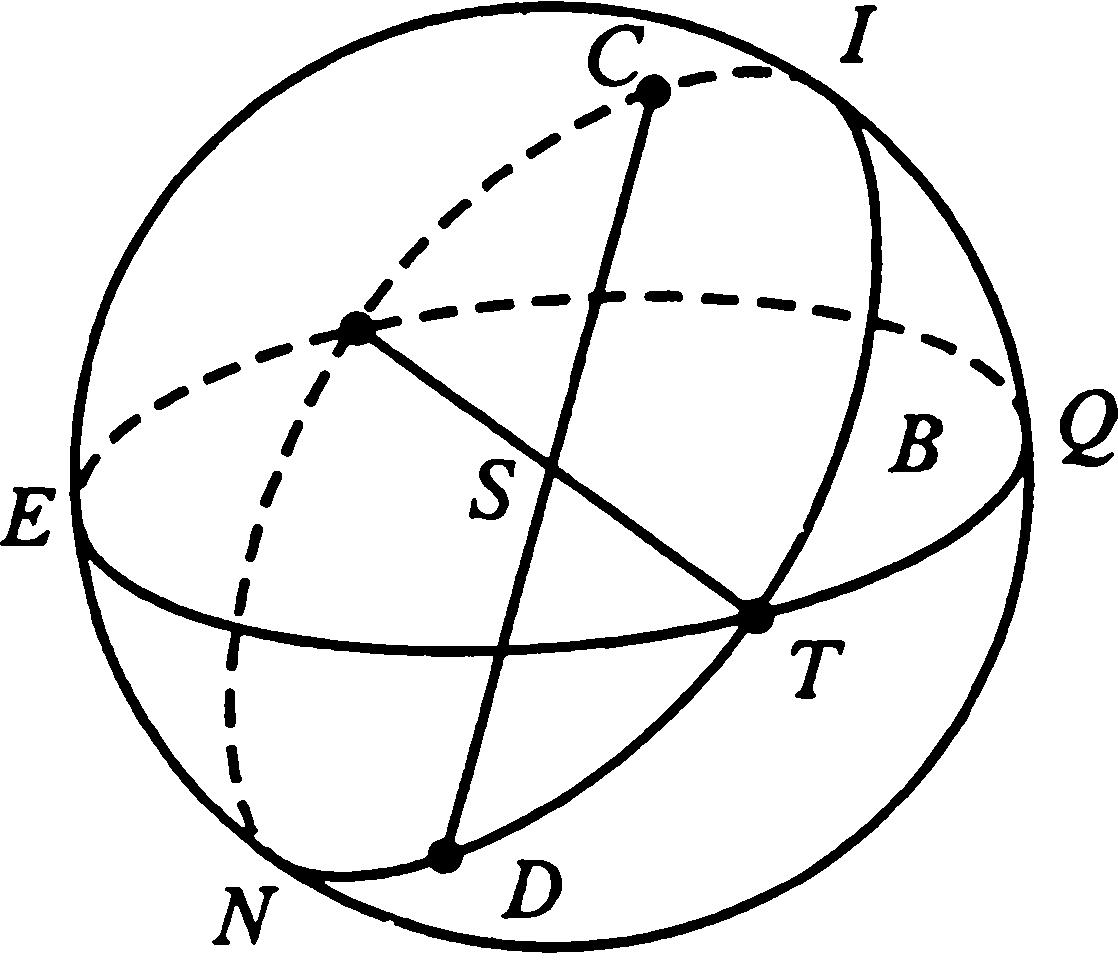
2. Ж.Н. Делиль. Новый способ рассмотрения видимых и действительных движений комет относительно Солнца (зач[итано] 17 [и 20] декабря 1744 г.)¹

Принимая во внимание, что линии, проведенные в плоскости эклиптики по наблюденным долготам комет, могут служить лишь для того, чтобы представить, как эти долготы видны с Земли, и принимая во внимание, что для представления широт следует вообразить себе другие линии, наклонные к первым на величину наблюденной широты, я попытался представить каждую наблюденную долготу и широту не только одной линией, но и еще одной линией, которая представляет видимое положение кометы таким, каким оно должно быть видно с Солнца, хотя оно и получено по ее долготе и широте, наблюдавшимся с Земли. То, что мне удалось сделать, это рассмотреть, каким образом любой луч зрения, идущий от Земли к комете, был виден с Солнца.

Луч зрения, по которому комета видна с Земли в любой момент своего появления, есть прямая линия. Если вообразить плоскость, которая проходит через каждую из этих линий [и] центр Солнца, то эта плоскость отсечет по большому кругу поверхность сферы, описанной вокруг центра Солнца. Именно с помощью этого большого круга, проведенного на этой сфере, я и представляю себе любой луч зрения, по которому комета видна с Земли.

Титульный лист рукописи Ж.Н. Делили «Новый способ рассмотрения видимых и действительных движений комет относительно Солнца»

Если даны долгота и широта кометы, видимые с Земли, то дано и положение вышеупомянутого круга, потому что он должен проходить через точку эклиптики, под которой Земля видна с Солнца. И можно вычислить с помощью простой аналогии угол, который образует этот большой круг с эклиптикой, как это будет видно из объяснения первой фигуры.

Пусть плоскость, проходящая через точки 1, 2, 3, 4, представляет собой плоскость эклиптики, на которой находится Земля, предположим, в точке T, откуда Солнце видно по направлению бесконечной [прямой] линии TS, расположенной на той же плоскости. Пусть также TA, TA и т. д. — разные лучи зрения, по которым комета видна с Земли в разные моменты своего появления. Я предполагаю [далее], что из некоторой точки A на каждом из этих лучей зрения опущены перпендикуляры A1, A2, A3, A4 и что через точки 1, 2, 3, 4, где эти перпендикуляры встречают эту плоскость, и через центр Земли T проводятся бесконечные [прямые] линии T1, Т2, ТЗ, Т4, которые представляют собой линии наблюденных долгот кометы, приведенные к [плоскости] эклиптики. Углы ∠ST1, ∠ST2, ∠ST3, ∠ST4, образованные в плоскости эклиптики вышеупомянутыми линиями с линией TS, проведенной от Земли к Солнцу, будут представлять, следовательно, видимые элонгации кометы от Солнца, которые легко будет вывести из наблюдений, сравнивая наблюденную долготу кометы с вычисленной долготой Солнца для того же самого момента времени.

Фиг. 1

Я предполагаю [затем], что последовательность знаков [Зодиака] отсчитывается по порядку чисел 1, 2, 3, 4 так, что, вычитая долготу Солнца из наблюденной долготы кометы, получим расстояние или элонгацию кометы от Солнца, отсчитанную в направлении знаков. Эта элонгация может оказаться, так же как и фигура, ее представляющая, в разных четвертях эклиптики, [в зависимости] от места, которое занимает здесь Солнце, а именно: в ST1 — когда элонгация меньше четверти круга или трех знаков; в ST2 — когда она больше трех знаков и меньше шести; в ST3 — когда она больше шести знаков и меньше девяти, и т. д.; наконец, в ST4 — когда она больше девяти знаков.

Видно также, что углы ∠AT1, ∠AT2, ∠AT3, ∠AT4 представляют собой наблюденные широты комет и равны им. Эти широты могут быть северными или южными. Я предполагаю, что те из них, которые выше плоскости T1, 2, 3, 4, будут северными, а другие — южными. Легко заметить и без того, что я об этом говорил, что в каком бы месте ни предположить выбранной точку A на любом луче зрения TA, это ничего не изменит ни в углах широт, ни тем более в углах видимых элонгаций кометы от Солнца.

Затем я предполагаю, что через точки 1, 2, 3, 4, определенные так, как я сказал [выше], на плоскости эклиптики, проведены перпендикуляры 1B, 2B, 3B, 4B к линии TS, которая соединяет центры Солнца и Земли. Эта линия [может] быть продолжена в ту и другую сторону настолько, насколько это будет необходимо. И наконец, соединив точки A, B, увидим, что плоскости ATB — это те, о которых я хотел поговорить выше и которые проходят через Солнце и через любой луч зрения кометы, видимой с Земли, и что углы ∠AB1, ∠AB2, ∠ABЗ, ∠AB4 измеряют наклон этих плоскостей к плоскости эклиптики.

Для того чтобы определить величину этого наклона, как например величину наклона ∠AB1, рассмотрим два прямоугольных треугольника ΔATI, ΔBT1. Оба они имеют прямые углы при [точке] 1 и одну и ту же высоту A1. И следовательно, взяв эту высоту в качестве радиуса круга, центром которого пусть будет точка A, [и описав окружность, мы найдем, что] основания 1T, 1B этих же самых треугольников будут тангенсами углов ∠1AT, ∠AB1, являющихся дополнениями до четверти круга, а углы ∠AT1, ∠AB1 представляют собой наблюденную широту кометы и искомый наклон. Но так как треугольник ΔBT1 образует в плоскости эклиптики еще прямой угол в [точке] B, видно, что две те же самые линии 1T, 1B находятся между собой в [таком же] отношении, как полный синус к синусу элонгации ∠BT1 кометы от Солнца. Итак, для того чтобы получить наклон ∠AB1, нужно лишь провести эту аналогию. Так как 1T: 1B равно полному синусу, то отношение полного синуса к синусу элонгации ∠BT1 [будет], таким образом, [равно отношению] тангенса дополнения наблюденной широты ∠AT1 к тангенсу дополнения наблюденного наклона ∠AB1:²

(1T: 1B) / sin ∠BT1 = tg ∠AT1 / tg ∠AB1.

С помощью [первой] фигуры легко видеть, что нужно делать, когда элонгация кометы от Солнца больше трех, шести или девяти знаков [Зодиака]. Когда она больше трех знаков и меньше шести, нужно взять ее дополнение до полукруга, что даст угол ∠BT2. Но когда элонгация будет больше шести знаков и меньше девяти, здесь нужно будет вычесть шесть знаков, и в остатке получим угол ∠BT3. И наконец, когда элонгация будет больше девяти знаков, здесь понадобится взять дополнение ко всему кругу в целом, что даст угол A ВТ4. И во всех этих трех случаях следует использовать углы ∠BT2, ∠BTЗ, ∠BT4 таким же образом, как было сказано выше относительно угла ∠BT1.

Прежде чем идти дальше, нужно рассмотреть, каким образом должен меняться наклон ∠AB1, ∠AB2 и т. д. плоскости ATB к плоскости эклиптики в зависимости от изменения угла ∠ST1, ∠ST2 и т. д. элонгации кометы, когда широта не меняется.

1. Вполне понятно, что когда угол элонгации кометы от Солнца есть нуль или же комета и Солнце [находятся] в видимом соединении, то плоскость ATB перпендикулярна плоскости эклиптики.

2. После соединения кометы с Солнцем, по мере того как элонгация кометы от Солнца ∠SBT1 возрастает до четверти круга или трех знаков, наклон ∠AB1 должен уменьшаться и в квадратуре этот наклон должен быть равен видимой широте [места], где наблюдалась комета.

3. Когда элонгация кометы от Солнца [находится] во второй четверти, т. е. если эта элонгация возрастает от трех до шести знаков, то наклон ∠AB2 должен возрастать до 90°.

Когда [же] элонгация равна шести знакам, это означает, что комета и Солнце находятся в противостоянии.

4. В шести последних знаках элонгации кометы от Солнца, а именно [когда элонгация равна] ∠ST3, ∠ST4, наклон ∠ABЗ, ∠AB4 должен иметь те же самые изменения [в смысле] уменьшения и увеличения, как и в шести первых знаках элонгации, но в другую сторону. После противостояния, до тех пор пока элонгация не достигнет девяти знаков, этот наклон должен уменьшаться, а когда элонгация станет равной точно девяти знакам, этот наклон будет самым малым, насколько возможно, и он должен быть равен видимой широте кометы. И наконец, при элонгации, [находящейся] в последней четверти, вышеупомянутый наклон должен снова возрастать, до тех пор пока наконец он не станет равным 90° на круге элонгации или комета не придет в соединение с Солнцем, откуда я начал свое рассмотрение.

Можно вычислить также с помощью одной лишь аналогии угол ∠STA видимого расстояния кометы от Солнца при наблюдении с Земли, так как угол ∠ABT прямой, так же как и угол ∠1ВТ. Если принять общую сторону TB за радиус круга, центр которого находится в точке Г, то линии B1, BA будут тангенсами противолежащих [им] углов ∠BT1, ∠BTA. Но известно отношение этих линий B1: BA, которое — то же самое, что и отношение синуса дополнения наклона ∠AB1, найденного выше, к полному синусу. Итак, с помощью этой аналогии можно было бы узнать угол, [на который комета удалена от Солнца при наблюдении] с Земли: ∠ATB или ∠STA. Поскольку синус дополнения прежде найденного наклона [делится] на полный синус, то и тангенс элонгации ∠BT1 будет [относиться] к тангенсу искомого угла ∠BTA, который измеряет, как было сказано, видимое расстояние кометы от Солнца так, как оно наблюдается с Земли.

Можно найти еще и другим способом угол ∠STA — видимое расстояние кометы от Солнца — с помощью наблюденной долготы и широты кометы. Пусть [мы имеем] обычную сферу (фиг. 2), т. е. сферу, описанную вокруг Земли как центра. Если большой круг этой сферы ABDF представляет собой эклиптику, то полюс ее будет P. Пусть точка A представляет место Солнца, а точка B или D — наблюденную долготу кометы, приведенную к эклиптике, и, наконец, дуга ⌣BC или ⌣DE — наблюденную широту кометы. Видно, что если вообразить себе большой круг ACE, проходящий через Солнце и комету, и дугу ⌣AC или ⌣AE — видимое расстояние кометы от Солнца, то она будет гипотенузой сферического треугольника ΔABC, прямоугольного в [точке] B, в котором известны две стороны прямого угла.

Фиг. 2

Если вычислить угол ∠STA — видимое расстояние — таким образом, как сказано в объяснении первой фигуры, то видно, что, если элонгация кометы от Солнца была бы больше трех знаков, следовало бы взять вместо угла ∠BT1 один из углов ∠BT2, ∠BTЗ, ∠BT4, т. е. дополнение до полукруга или до целого круга вышеупомянутой элонгации, как я говорил выше. Но в этих случаях видно также, что угол ∠BTA видимого расстояния кометы от Солнца, который в трех первых знаках элонгации всегда будет меньше четверти круга, здесь будет точно равен четверти круга, когда элонгация будет три или девять знаков. Но когда элонгация будет больше трех и меньше девяти знаков, угол ∠BTA будет найден таким образом, как только что говорилось. Для того чтобы получить видимое расстояние ∠STA кометы от Солнца, наблюдавшееся с Земли, здесь следовало бы взять [его] дополнение до полукруга.

Угол ∠STA — видимое расстояние кометы от Солнца, к которому я обращусь в следующем упрощении, — угол, [наблюдаемый] с Земли, может служить для нахождения кратчайшего действительного расстояния SC Солнца от луча зрения TA или самого короткого реального расстояния от Солнца до кометы, [которая находится] в некоторой точке на данном луче зрения ТА. Для этого нужно лишь добавить к предшествующим определениям определение действительного расстояния Солнца от Земли, которое выводится из астрономических таблиц для момента каждого наблюдения.

Итак, предположим, что это расстояние TS известно по нескольким положениям кометы, из которых среднее расстояние Солнца от Земли выведено как 100 000. Если представим себе перпендикуляр SC, отпущенный из центра Солнца S на луч зрения TA, то этот перпендикуляр будет измерять кратчайшее расстояние от этого луча. И видно, как легко можно найти величину этого перпендикуляра SC, а заодно и расстояние TS Солнца от Земли. Для этого следует лишь составить такое отношение: полный синус [так относится к] синусу угла [расстояния кометы от Солнца, наблюдаемого] с Земли, ∠STC, как расстояние TS Солнца от Земли [относится] к искомому кратчайшему расстоянию SC:

sin tot /sin ∠STC = TS/SC.

Хотя еще не определена ни точка A, в которой находится комета на луче зрения TA при каком-либо наблюдении, ни ее истинное расстояние от Солнца, когда она находится на этом луче, видно, однако, что она не может находиться к Солнцу ближе, чем на величину перпендикуляра SC.

Если предположить еще, что на луче зрения ACT взяты две какие-нибудь точки A, D, равноудаленные в ту и другую сторону от точки C на известное расстояние, или же построить углы ∠CSA, ∠CSD некоторой известной величины, имея в виду, что они не превышают 90°, то легко будет вычислить реальные расстояния кометы от Солнца SA или SD и в тех же частях, в которых выражено самое кратчайшее расстояние SC. Для этого нужно лишь составить это соотношение: полный синус одного из углов ∠CSA, ∠CSD так относится к кратчайшему расстоянию SC, как полный синус относится к расстоянию SA или SD, которое требуется найти:

(sin tot ∠CSA) / SC = (sin tot ∠CSD) / SC = sin tot / SA = sin tot / SD.

Как я говорил выше, мой метод состоит в том, чтобы представить себе сферу, описанную вокруг центра Солнца S, и рассмотреть сечение, которое производит на этой сфере плоскость STA во время каждого наблюдения. Если представить себе с помощью фиг. 3 и 4 часть этой солнечной сферы, имеющей Солнце S в качестве центра, и круг ETQ, представляющий собой эклиптику, на которой я предполагаю, что точка T показывает видимое место Земли при наблюдении с Солнца, то пусть также большой круг ITN представляет собой сечение, которое отсекает на этой солнечной сфере плоскость STA (фиг. 1). Угол ∠ITQ или ∠ETN (фиг. 3, 4) будет, следовательно, углом наклона ∠AB1, найденным с помощью первого отношения, определенного выше. И следовательно, нужно рассмотреть в этих углах наклона ∠ITQ или ∠ETN все варианты, о которых я говорил выше, в соответствии с разной величиной видимой элонгации кометы от Солнца, выведенной из наблюдений.

Кроме того, поскольку угол ∠CST (фиг. 1), дополняющий угол от Земли ∠ATS, измеряет самое близкое к Солнцу гелиоцентрическое расстояние Земли от точки C на луче зрения TA, то, если взять на окружности ITN (фиг. 3, 4), которая представляет собой этот луч зрения, дугу ⌣BT, равную этому углу от Солнца ∠CST (фиг. 1), точка B будет представлять собой точку наиболее близкого реального расстояния кометы от Солнца, величина которого определяется тем способом, как говорилось выше.

Фиг. 3

Если взять на окружностях ITN в ту и другую сторону от точки B дуги ⌣BC и ⌣BD, каждую по 90°, то точки C и D будут крайними точками, в которых комета может находиться на полуокружности ITN, потому что комета может соответствовать этим точкам, которые находятся на бесконечном расстоянии от Солнца. Итак, комета может находиться только на полуокружности CBD. Если она находится в точке B, то она будет на самом близком, насколько возможно, реальном расстоянии от Солнца и будет удалена от этой точки B к C или к D. Она будет также реально удалена от Солнца до бесконечности.

Для того чтобы сделать предыдущую теорию пригодной для определения места комет, я рассмотрел [следующие положения].

Фиг. 4

1. Что одно-единственное наблюдение кометы по долготе и широте не определяет ее точного места, видимого с Солнца, а лишь то, что она должна оказаться где-нибудь на этой полуокружности, в данном положении относительно эклиптики. Что известно, кроме того, самое близкое, насколько возможно, реальное расстояние кометы от Солнца, а также точка, до которой доходит это самое близкое расстояние. И наконец, что известно еще действительное расстояние кометы от Солнца в некоторой точке и то, что это расстояние проходит через вышеупомянутую полуокружность, имея в виду, что известно расстояние от этой точки до точки на самом большом расстоянии.

2. Второе наблюдение при сравнении с первым может определить почти точное место кометы, видимой с Солнца. И это с помощью точки пересечения полуокружности этого второго наблюдения с полуокружностью первого. Я говорю почти, потому что предполагается, что от одного наблюдения до другого комета имеет реальное движение, не иначе как лишь приближение прямо к Солнцу или удаление от него, без изменения ее видимого места. Так как можно определить точки пересечения двух больших окружностей на третьей, то можно узнать, каковы действительные расстояния кометы от Солнца в каждом наблюдении. А следовательно, можно увидеть, приближается ли комета к Солнцу в действительности или же удаляется от первого наблюдения до следующего. И наконец, можно узнать, насколько она действительно приблизилась или удалилась.

3. Третье наблюдение в соединении с двумя первыми могло бы показать, верно или ложно сделанное предположение о том, что реальное движение кометы точно направлено к Солнцу, и оно могло бы служить для исправления этого предположения. Ибо если полуокружность места кометы в третьем наблюдении не пересекается с двумя первыми полуокружностями в точках, где они пересекались, это признак того, что в интервале между этими тремя наблюдениями комета не двигалась по линии, точно направленной на Солнце, или же то, что комета изменила свое видимое место, наблюдаемое с Солнца.

В случае, когда комета имела видимое движение на сфере Солнца, ее истинное место в момент любого наблюдения не должно было быть ни в какой из трех вышеупомянутых точек пересечения. Но ее видимый путь, наблюдаемый с Солнца, должен был бы встречать каждую из трех вышеупомянутых полуокружностей в разных точках, последовательно проходя через полуокружность первого наблюдения, через полуокружность второго и через полуокружность третьего.

Для определения видимого пути кометы, наблюдаемого с Солнца, по трем наблюдениям нужно вообразить себе большой круг сферы, две дуги которого пересекаются тремя вышеупомянутыми полуокружностями пропорционально интервалам времени, протекшим между наблюдениями, и нужно еще, чтобы реальные расстояния кометы от Солнца, соответствующие трем этим точкам пересечения, не изменялись. Или если они изменяются, то это изменение должно составлять величину, пропорциональную тем же самым интервалам времени. Вот каким образом я рассуждал, чтобы можно было всегда определить по трем точным и очень близким друг к другу наблюдениям отрезок истинного пути кометы.

Предположение, которое я здесь делаю, о том, что видимое движение комет, наблюдаемое с Солнца, должно быть равным за равные промежутки времени, так же как и изменение их действительных расстояний от Солнца, не должно вызывать трудностей, потому что в природе реального или видимого движения нет ничего неравномерного, что могло бы, будучи учтено на больших интервалах [времени], считаться между тем нечувствительным на очень малых промежутках. На практике речь идет лишь о фиксировании длительности этих промежутков.

Именно это я только что и сделал убедительным способом, потому что я считаю, что приложением тех же самых правил к планетам [были получены их] теории, которые уже известны. Ибо если я могу по этим правилам определить с помощью наблюдений истинные расстояния и реальные движения планет такими, какими они, впрочем, и известны, то было бы неверно сомневаться в том, что эти правила, приложенные к наблюдениям комет, не могут служить для определения также и их истинных расстояний и реальных движений, а следовательно и для доказательства их теорий, столь же независимо от гипотез, которые можно выдвинуть с помощью наблюдений.

Нужно здесь хорошо отличать предположение от гипотезы. Я только что сказал о предположении, которым, как я полагаю, можно воспользоваться для определения различных точек или маленьких дуг истинного пути кометы. [Это предположение] было бы столь же необходимо не только для определения этого пути, без допущения [каких-либо] гипотез, но также и для того, чтобы доказать закон, которому комета следует в своем движении. [И это] вместо того, чтобы, как г. Ньютон и те, кто за ним следуют, определять до сих пор (насколько я мог узнать) теории комет ощупью и приблизительно, следуя гипотезам. Потому что они искали среди различных истинных путей, которые могла иметь любая комета, тот, который она имела бы, следуя законам Кеплера или же гипотезе, по которой их движение было бы тем же самым, что и движение других планет.

Примечания

1. Эта работа Делиля была зачитана на заседании Конференции Петербургской Академии наук 17 декабря 1744 г., а 20 декабря он объяснял свои чертежи (см.: Протоколы заседаний Конференции Имп. Академии наук с 1725 по 1803 год. СПб., 1899. Т. II. С. 45—46). Предназначенная для печати, она осталась неопубликованной. В настоящее время рукопись хранится в Санкт-Петербургском филиале Архива РАН (р. 1, оп. 1, д. 88, л. 1—13). Это французский автограф Делиля: Nouvelle manière de considérer les mouvements apparentes et réels des comètes à l'égard du Soleil.

2. В оригинале Делиля формулы и символы отсутствуют, соотношение дается словами, в тексте. Для удобства восприятия современным читателем в русском переводе помимо записи Делиля дана и привычная запись в виде формулы.