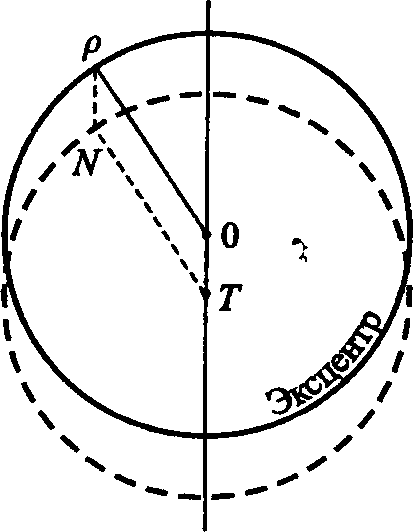
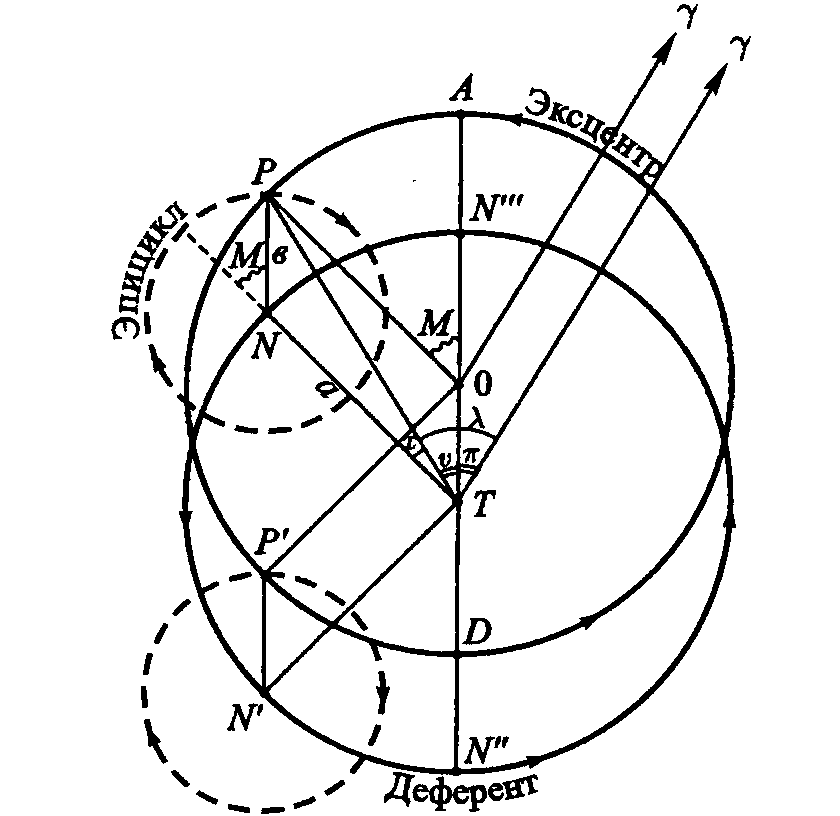
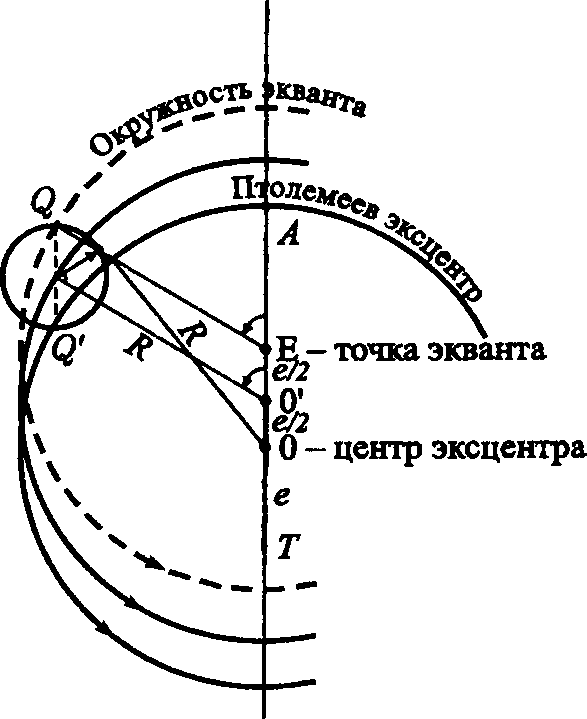
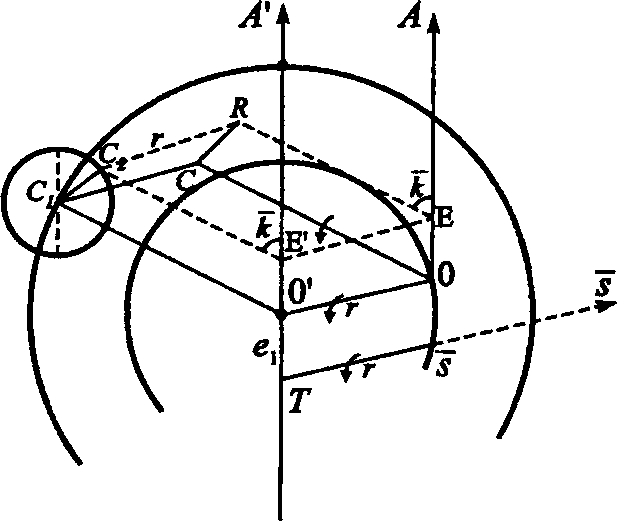
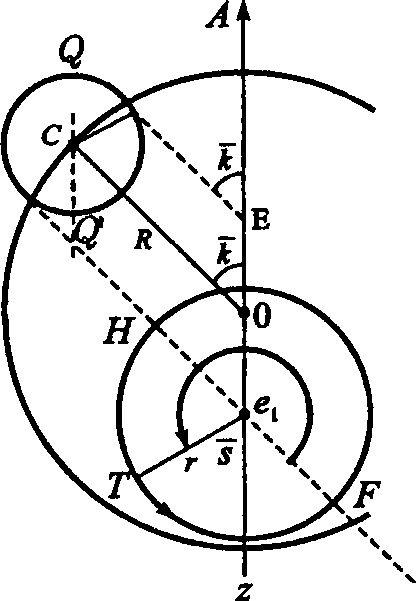
Приложение

В данном приложении приводится более детализированная по сравнению с изложенной в основном тексте картина перехода от гео- к гелиоцентрической теории.

Уже в Commentariolis Коперник использовал кинематико-геометрическую модель движения планет по долготе, разработанную Ибн аш-Шатиром (ум. 1375) — астрономом и математиком Марагинской обсерватории¹, добавив к ней идею гелиоцентризма, гелиоцентрического объяснения второй («солнечной») аномалии.

Рис. 7. Модель эксцентра

Прежде чем переходить к рассмотрению построений аш-Шатира и Коперника напомним, что движение планеты уже в древности описывалось как в терминах модели «деферент-эпицикл», так и в терминах модели эксцентра. Впрочем, иногда использовали «совмещенную» модель: эксцентр эпицикл. Сам Птолемей часто предпочитал последнюю, поскольку такое описание проще.

Представители восточного направления (а это в первую очередь ученые, работавшие в Марагинской обсерватории (основана Надиром аль-Дин аль-Туси в 1259 г.) — аль-Урди (ум. 1266), аль-Туси, аль-Ширази, Ибн аш-Шатир и др. — разрабатывали хитроумные математические модели планетных движений. В частности, они для каждой планеты искали такую точку, при наблюдении из которой угловая скорость центра эпицикла (N) в его движении по деференту была бы постоянной (подр. см.: Sayili A., 1960; Huff T.E., 1993. P. 51—62; 179—186; Kennedy E.S., Roberts V., 1950; Swerdlow N., 1973; Saliba G., 1984; Saliba G., 1987).

Рис. 8. Взаимосвязь моделей эксцентра и эпицикла

Историками астрономии выдвигались разные гипотезы о том, каким образом достижения марагинских астрономов стали известны Копернику. Многие исследователи сходятся на том, что соответствующую информацию Коперник мог почерпнуть из византийских источников, попавших в Италию в XV в.

В основе модели эксцентра лежит мысль о том, что место наблюдения (т. е. положение Земли) не совпадает с геометрическим центром орбиты, что позволяло, в частности, объяснить неравномерность видимого с Земли движения планет, сохранив одновременно постулат о равномерном круговом движении планеты вокруг геометрического центра мира (рис. 7).

Рис. 9. Геометрическое построение аш-Шатира.

Согласно теореме, приписываемой Аполлонию Пергскому (ок. 200 г. до н. э.) обе модели (эксцентра и эпицикла) при соблюдении определенных условий эквивалентны: «Пусть точка N обращается вокруг центра T по деференту с постоянной угловой скоростью, а точка P (планета) обращается по эпициклу с той же угловой скоростью, но в противоположном направлении. Тогда движение этой планеты (т.е. точки P) будет таким, как если бы она обращалась с той же угловой скоростью и в том же направлении вращения по окружности эксцентра, радиус которой равен радиусу деферента, а центр O смещен относительно центра T на отрезок OT (эксцентриситет эксцентра), равный и параллельный радиусу PN» (рис. 8).

Теперь о теории аш-Шатира. Марагинскай астроном осуществил следующее геометрическое построение: из некоторой точки O′ на отрезке OE (рис. 9) он провел отрезок O′C₁ равный радиусу R в модели Птолемея (окружности, отрезки и точки, относящиеся к этой модели — в варианте эксцентра — на рис. 9 обозначены черным цветом). Точка C₁ будет далее рассматриваться как центр эпицикла радиуса r′ = O′E. Пусть по этому эпициклу вращается точка C₂ в том же направлении, в каком точка C₁ вращается около своего центра O′ и с той же угловой скоростью, причем угол вращения радиуса r′(k) отсчитывается от отрезка C₁O′. Кроме того, < C₂C₁O′ =< AO′C₁ по построению.

Таким образом, в модели аш-Шатира вводится новый эксцентриситет TO′ для окружности с центром O′. Чтобы эта модель была по возможности близка модели Птолемея, были введены следующие граничные условия для положения точки C₁ на линии апсид (когда угол k = 0 и C₂ совмещается с точкой A):

(R − r′) + (e − r′) = R,

где e = EO.

При соблюдении этого условия точка C₂, попав на линию апсид, окажется в точке A (на птолемеевском эксцентре).

Отсюда

r′ = e/2.

Далее, нетрудно убедиться, что

e′ = TO′ = (3e)/2.

Как видно из рис. 9, точки C₂ и P, хотя и расположены близко одна к другой (в силу малости эксцентриситета), нигде, кроме как на линии апсид, не совпадают, но обе они — и это очень важно! — лежат на одной прямой EQ, т. е. на радиусе экванта E, а потому угол к увеличивается равномерно, т. е.

— точка C₂ равномерно (с постоянной угловой скоростью) вращается около центра C₁ эпицикла;

— точка C₁ равномерно вращается около центра O′ деферента аш-Шатира.

Заметим, что в модели Птолемея планета P не двигалась равномерно около центра деферента. Кроме того, модель аш-Шатира сохраняла равномерность движения точки C₂ относительно точки экванта E. Эти обстоятельства были важны для Коперника, упрекавшего Птолемея в нарушении принципа равномерного кругового движения.

Обратимся теперь к модели движения внешних планет, предложенной в Commentariolis и развитой затем в De Revolutionibus. Что сделал Коперник? Саму модель аш-Шатира он не тронул, но заменил в точке T Землю средним Солнцем, а в точку C₂ поместил планету. Тем самым равномерное движение планеты P относительно экванта в модели Коперника было сохранено, как фактически и сам эквант².

Несколько смущало, правда, то, что реальное движение планеты в модели аш-Шатира — Коперника оказалось несколько отличным от кругового, поскольку траектория точки C₂, в которую польский астроном поместил планету, вообще говоря, не совпадала с круговой (относительно точки O) траекторией в модели Птолемея. «...В этом сложном движении, — замечает Коперник, — светило не опишет точного круга, как думали древние математики, однако разница будет нечувствительной (differentia tamen insensibili)»³.

Итак, в птолемеевой модели эксцентра планета P движется по окружности, центр которой O удален от центра Земли (T) на расстояние e; при этом отрезок EP равномерно обращается вокруг точки экванта (E).

В модели Коперника планета P участвует одновременно в двух движениях: в равномерном круговом движении по деференту радиуса R с центром O′, удаленным от среднего Солнца (которое Коперник поместил в точку T) на расстояние (3e)/2; а также в равномерном круговом движении по эпициклу с центром C₁ и радиусом r′ = e/2. В целом, такое двойное движение планеты по долготе практически неотличимо от ее движения по кругу радиуса R с центром O.

В обеих моделях планета движется с постоянной угловой скоростью относительно точки экванта (E). Движение же ее относительно Солнца в модели Коперника неравномерно, как и ее движение относительно Земли в модели Птолемея.

Трансформация предложенной аш-Шатиром и принятой Коперником модели движения внешней планеты в гелиоцентрическую форму представлена на рис. 10. Точки S (положение среднего Солнца) и O (центр птолемеева эксцентра) фиксированы; точке T (центр Земли) придается вращение вокруг точки S̄, а точке O′ — около точки (т. е. рассматривается вращение против часовой стрелки шарнирного параллелограмма O′TS̄O вокруг фиксированной стороны SO).

Рис. 10. Модель аш-Шатира в гелиоцентрическом варианте

В другом построенном на рис. 10 параллелограмме C₁C₂PC, точка P изображает планету, вращающуюся вокруг центра C эпицикла в гелиоцентрической модели. Точка E определяет гелиоцентрическое положение экванта на линии апсид SA (E′O′ = EO). Заметим, что точка P (планета) равномерно вращается относительно точки E (это вращение характеризуется углом k).

Рис. 11. Гелиоцентрическая модель для верхней планеты.

В итоге получается гелиоцентрическая модель движения внешней планеты⁴, представленная на рис. 11. Это модель типа «эксцентр + эпицикл», но Коперник упомянул и о возможности использовать также модель типа «эксцентр + 2 эпицикла».

Построение кинематической гелиоцентрической модели движения внутренних планет потребовало преодоления ряда существенных трудностей, на чем, однако, я здесь не буду останавливаться⁵, замечу лишь, что и в этом случае Копернику помогли находки астрономов Марагинской обсерватории.

Примечания

1. К XII в. в арабо-исламском мире обозначились два направления в развитии нептолемеевских методов моделирования планетных движений — западное и восточное. Для представителей западного направления (испано-арабский регион) характерно было стремление привести птолемеевские модели в соответствие с космологическими принципами Аристотеля. При этом многие авторы вообще отбрасывали понятия эксцентра и эпицикла, довольствуясь теорией гомоцентрических сфер Эвдокса и Аристотеля. Примером может служить трактат аль-Битруджи «Принципы астрономии» (подр. см.: Григорьян А.Т., Рожанская М.М., 1980. С. 178—181; Sabra A.I., 1994.

2. Подр. см.: Neugebauer O., 1968. P. 92—96. — Поэтому утверждения, будто Коперник вообще отказался от идеи экванта «l'abandon de l'équant, ce haut titre de gloire de l'astronomie copernicienne» (Histoire Générale des Science, 1957—1964. P. 64), вряд ли имеют основание.

3. Коперник Н., 1964. С. 310. — Действительно, PC² ≅ e²sin²k/(2R), т. е. при k = 90°PC² ≅ e²/(2R). Для Марса (e ≅ 0,1) PC). = 0,005, т. е. поправка для видимого положения планеты составит около 0,3°.

4. Коперник Н., 1964. С. 293—311.

5. См. подр.: Swerdlow N., Neugebauer O., 1984. P. 369—371.