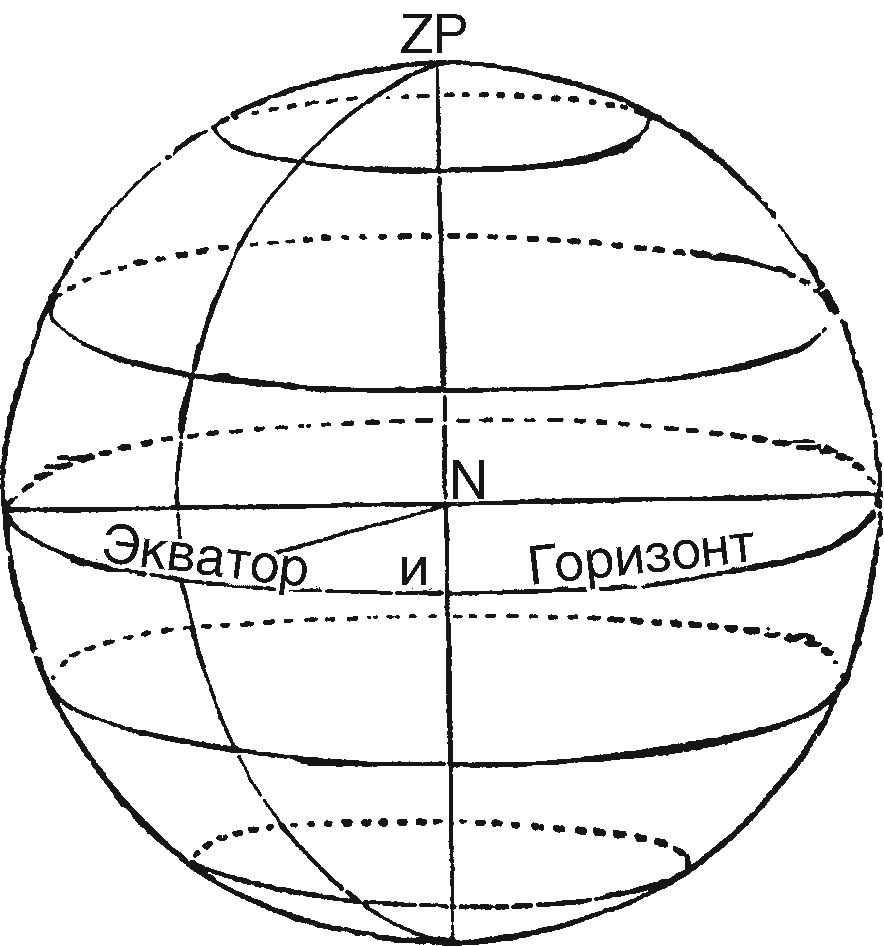
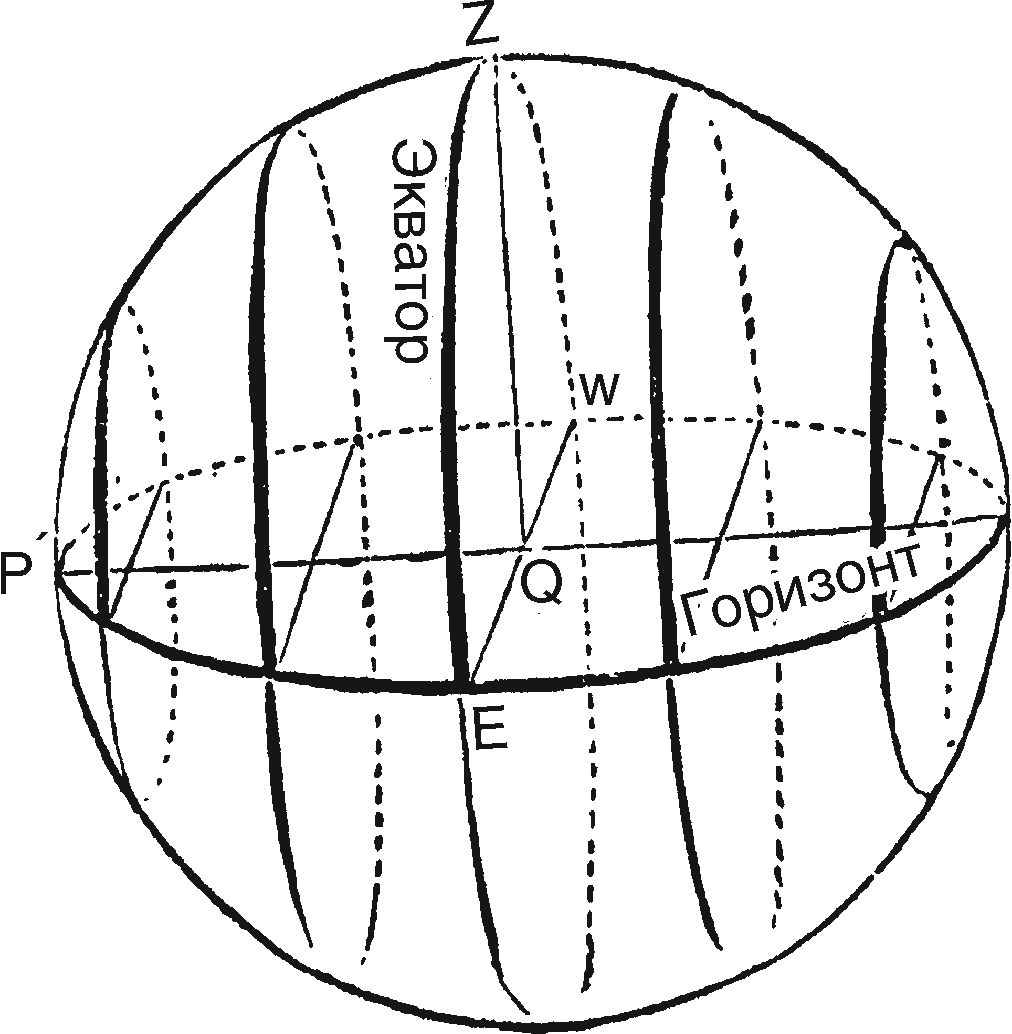
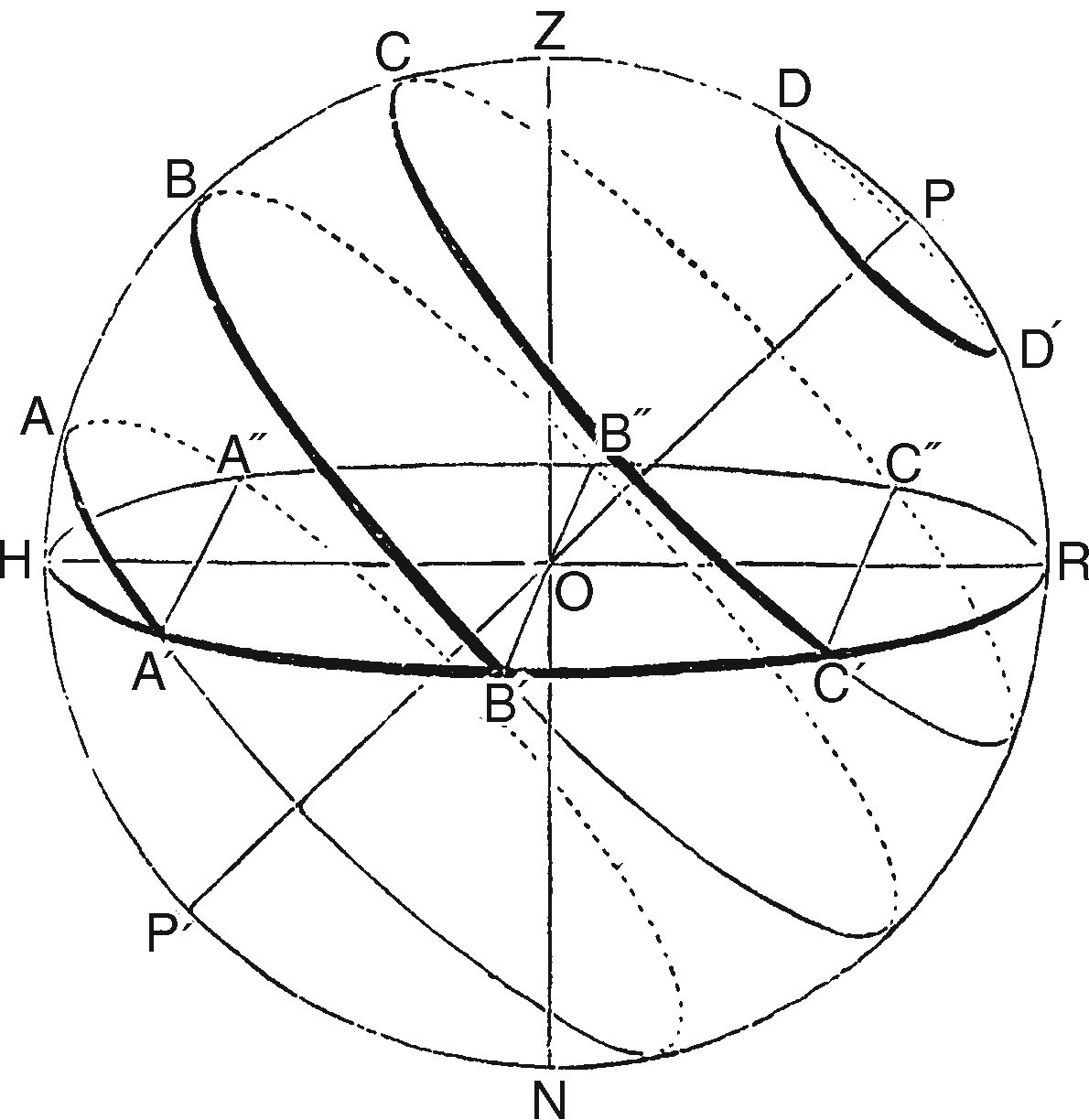
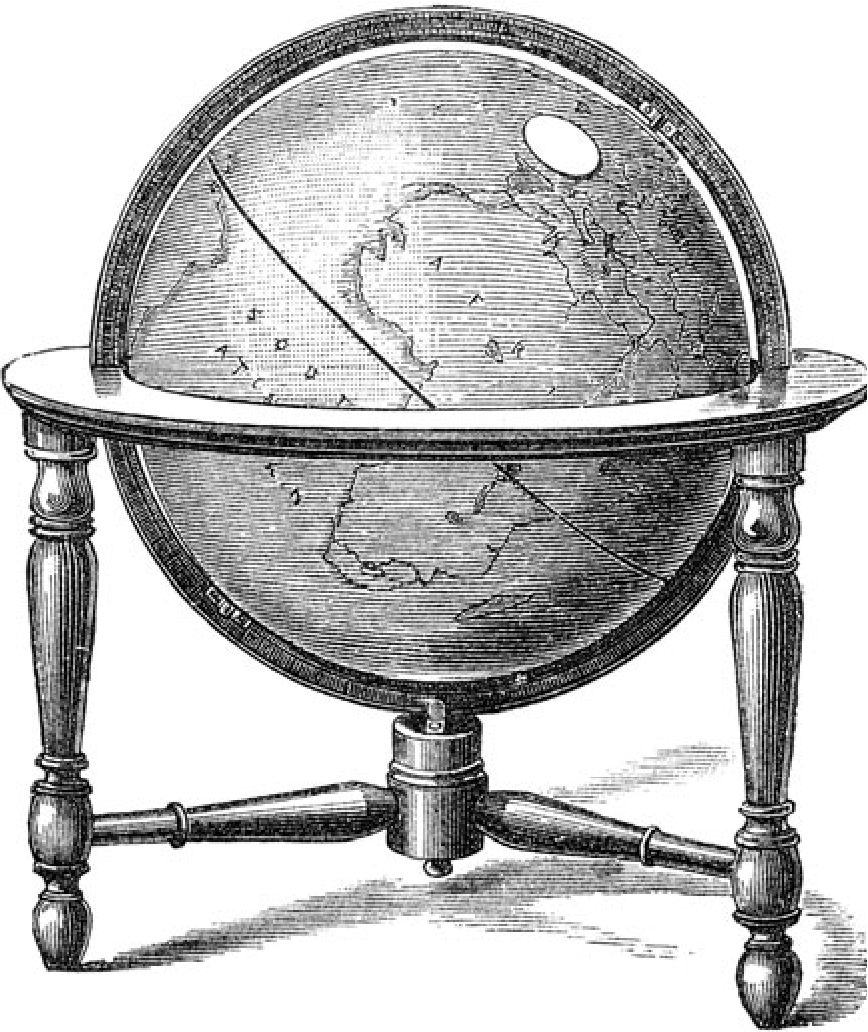
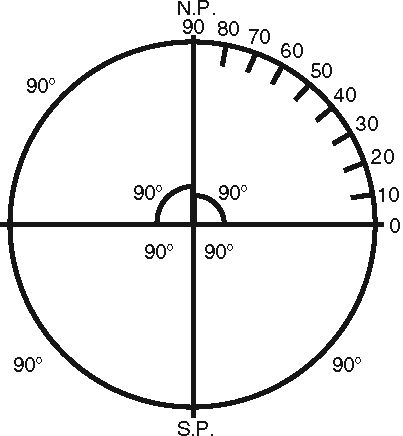
Глава 4. Два горизонта

Не только крайне важно для нашей темы, но и само по себе чрезвычайно интересно изучить некоторые астрономические проблемы, связанные с культом горизонта, который, как мы видели в предыдущей главе, был распространен среди древних народов Индии и Египта.

Прежде чем пойти дальше, мы должны как следует уяснить для себя, что такое горизонт, и для этого придется прибегнуть к некоторым схемам.

Видимое движение звезд с точки зрения наблюдателя на Северном полюсе

Горизонт в любой точке представляет собой окружность, ограничивающую видимую поверхность Земли, по которой, как кажется глазу, встречаются земля (или море) и небо. Дальше мы рассмотрим отношение горизонта конкретного места к видимому движению небесных тел в этом месте.

Маятник Фуко продемонстрировал вращение Земли вокруг своей оси, но, разумеется, такая мысль была совершенно чужда древним народам. Поскольку Земля вращается в пространстве, где ее со всех сторон окружают бесконечно отдаленные звезды, видимое движение звезд будет очень сильно зависеть от того места, где мы находимся на Земле; это можно показать при помощи нескольких иллюстраций.

Видимое движение звезд с точки зрения наблюдателя на экваторе

Наблюдатель, находящийся, к примеру, на Северном полюсе, увидит, что звезды движутся кругами, параллельно горизонту. Ни одна звезда не восходит и не заходит — половина небосвода всегда видна над горизонтом, другая половина всегда невидима; в то же время наблюдатель на Южном полюсе увидит половину звезд, невидимую наблюдателю на Северном полюсе, так как это именно та половина, которая находится ниже северного горизонта. Если наблюдатель находится на экваторе, видимое движение звезд будет таким, как на иллюстрации вверху, — то есть все звезды восходят и заходят, и каждая звезда, в свою очередь, половину времени находится над горизонтом и половину за горизонтом. Но если взять наблюдателя на средних широтах, скажем в Лондоне, то окажется, что некоторые звезды для него всегда над горизонтом, а другие всегда за горизонтом — иными словами, они никогда не заходят или не восходят. Все остальные звезды и восходят, и заходят, но некоторые из них находятся над горизонтом долгое время, а за горизонтом короткое, а другие находятся над горизонтом очень короткое время, а за горизонтом долгое.

Представим, что в воображаемой нулевой точке наблюдатель находится на широте 45° (то есть на половине пути между экватором с широтой 0° и Северным полюсом с широтой 90°), поэтому Северный небесный полюс будет на полпути между зенитом и горизонтом; близко к полюсу наблюдатель увидит, как звезды описывают круги, однако наклонные и на разном расстоянии от горизонта. Если переместить взгляд в сторону от полюса, то там звезды восходят и заходят по косой, описывая более широкие круги и постепенно больше и больше опускаясь за горизонт, пока не будут совершать половину своего пути за горизонтом, достигнув небесного экватора. Перемещаясь дальше на юг, мы увидим, что звезды все меньше и меньше поднимаются над горизонтом, и при этом так же, как северные звезды, которые никогда не опускались за горизонт, есть южные звезды, которые никогда не выходят из-за него. DD′ показывает видимый путь околополярной звезды; BB′B″ — путь и точки восхода и захода экваториальной звезды; CC′C″ и AA′A″ — пути звезд среднего склонения, одной северной и одной южной.

Небесная сфера с точки зрения наблюдателя на средних широтах. Наклонная сфера

Где бы мы ни находились на Земле, нам всегда кажется, что мы стоим на верхушке. Все древние народы разделяли идею, что Земля — обширная плоскость: по их представлениям, только известная им местность и окружающие земли находятся в центре плоскости. Платон, например, удовольствовался тем, что поместил Средиземноморье и Грецию на верхушку своего куба, а Анаксимандр поместил тот же район на верхушку своего цилиндра.

Очень удобно изучать условия наблюдения на полюсах, экваторе и в некоторых местах на средних широтах при помощи обычного глобуса. Деревянный «горизонт» глобуса параллелен горизонту места на верхушке глобуса, который можно изобразить с помощью линейки. Таким образом можно получить самое конкретное представление об отношениях горизонта наблюдателя на разных широтах к видимым траекториям звезд.

Далее мы рассмотрим астрономическое отношение между горизонтом любого места и культом солнца и звезд в моменты восхода и захода, когда они, само собой, находятся на горизонте или рядом с горизонтом; и чтобы приблизить наше рассмотрение к древним памятникам, удобно разобрать этот вопрос на примере Фив, где такие памятники наличествуют в большом количестве и самым тщательным образом описаны.

Глобус Земли с линейкой, показывающей различные условия наблюдения на средних широтах

Чтобы отрегулировать глобус для наших целей, нужно установить его на 25°40′ с. ш., или, иными словами, наклонить ось глобуса под этим углом к деревянному горизонту.

Сразу же станет очевидно, что там наклон оси к горизонту гораздо меньше, чем в Лондоне. Так как все звезды, проходящие между Северным полюсом и горизонтом, никогда не заходят, все их видимое движение будет происходить над горизонтом. Все звезды между горизонтом и Южным полюсом никогда не взойдут. Следовательно, звезды на расстоянии 25° от Северного полюса будут незаходящими в Фивах, а звезд на расстоянии 25° от Южного полюса там никогда не будет видно. По стечению обстоятельств все местности, которыми занимаются археологи, изучающие историю древних народов Египта, Вавилона, Ассирии, Китая, Греции и прочих, находятся на средних широтах, поэтому мы имеем дело с небесными телами, которые заходят, и небесными телами, которые никогда не заходят; причем высота полюса всегда не очень большая и не очень маленькая. На разных широтах наклон экватора к горизонту, как и высота полюса, будет варьироваться, но для каждого места будет строгое отношение между наклоном экватора и возвышением полюса. За исключением мест на самих полюсах, экватор будет пересекать горизонт в направлении прямо на восток и прямо на запад. Поэтому каждое небесное тело, которое восходит или заходит севернее экватора, будет пересекать горизонт между точкой востока или запада и точкой севера; а незаходящие небесные тела, разумеется, не будут пересекать горизонт совсем.

Солнце и звезды у экватора на широте Фив с виду будут восходить и заходить под не очень большим углом к вертикали; но если взять звезды, восходящие и заходящие рядом с точкой севера или юга на горизонте, они будут как бы скользить вдоль горизонта, а не восходить и заходить вертикально.

Итак, сразу же становится понятно, что должен быть четкий закон, соединяющий положение Солнца (или звезды) с местом его восхода и захода. Звезды на одном и том же расстоянии от одного из небесных полюсов будут восходить и заходить в одной и той же точке на горизонте, а если звезда не меняет свое ме

стоположение на небосклоне, она всегда будет восходить и заходить в одном и том же месте.

Амплитуды от точки востока или запада до Северного полюса, северной точки горизонта, и Южного полюса, южной точки горизонта

Здесь следует ввести несколько технических терминов. Каждое небесное тело, будь то Солнце, Луна, планета или звезда, в каждый конкретный момент времени занимает определенное место, которое частично, не полностью, определяется величиной, называемой склонением, то есть расстоянием от тела до небесного экватора. Это склонение представляет собой одну из двух необходимых нам координат, если мы хотим назвать точное положение любого тела на небесном склоне; и следует хорошо понимать, что если все эти небесные тела восходят и заходят, и восходят и заходят с точки зрения наблюдателя, то место их восхода и захода должно быть непосредственно связано с их склонением. Тела с одинаковым склонением будут восходить в одних и тех же точках горизонта. Если склонение меняется, то тело, разумеется, восходит и заходит в другой точке горизонта.

Теперь мы определим точки на горизонте, разделив окружность на четыре четверти по 90° каждая, всего 360°, так что у нас получаются азимуты по 90° от точки севера или юга до точки востока или запада.

Азимуты не всегда рассчитываются таким образом, навигация предпочитает один метод, а астрономия другой. Например, азимут можно рассчитать как расстояние в градусах от точки юга в направлении, проходящем через точки запада, севера и востока. В такой системе точка может иметь азимут от 0 до 360°.

Затем нам важно определить термин амплитуда. Амплитуда небесного тела на горизонте — это расстояние

от него до точки запада и востока на север или юг; она всегда измеряется до ближайшей от этих двух точек, таким образом, самое большое значение амплитуды не может превышать 90°. Например, сама точка юга будет иметь амплитуду 90° южнее точки запада или 90° южнее точки востока, тогда как точка 2° западнее точки юга будет иметь амплитуду 88° западнее точки юга, а не 92° восточнее точки юга.

Так можно сказать, что звезда с определенным склонением восходит или заходит с таким-то азимутом, если считать от точки севера на горизонте, или с такой-то амплитудой, если считать от экватора. Это одинаково относится и к южному (−), и к северному (+) склонению.

В представленной на с. 57 таблице содержатся амплитуды восхода или захода (север или юг) небесных тел со склонениями от 0° до +64° для Фив; небесные тела со склонениями больше 64° никогда не заходят в Фивах, если они на севере, и никогда не восходят, если они на юге, так как широта Фив (и соответственно возвышение полюса) около 26°.

Таким образом, из таблицы очевидно следует непосредственная связь между склонением небесного тела и амплитудой, с которой оно восходит и заходит: зная склонение, мы знаем амплитуду; зная амплитуду, мы знаем склонение.

Допустим, мы имеем дело с морским горизонтом: все небесные тела, восходящие и заходящие одновременно в некий момент времени, будут находиться на большом круге небесной сферы, так как плоскость видимого горизонта параллельна плоскости геоцентрического.

Однако есть и еще несколько дополнительных моментов, которые нужно иметь в виду. Обычно мы определяем, что при такой-то амплитуде склонение небесного тела, восходящего или заходящего с этой амплитудой, будет таким-то, при условии, что видимый горизонт соответствует морскому, или истинному. Но это не вполне верно, потому что обычно из-за рефракции мы видим солнце за некоторое время до того, как оно взойдет на самом деле, и еще некоторое время после того, как оно сядет. Поэтому если мы наблюдаем заход солнца, скажем, севернее точки запада, то мы знаем, что в момент, когда мы видим его заходящим, кажется, что оно чуть-чуть севернее, чем есть на самом деле в момент истинного захода, поскольку рефракция дает нам положение солнца чуть ниже истинного горизонта. Это мы должны иметь в виду во-первых. А во-вторых, как правило, мы, конечно, имеем дело не с морским горизонтом. То тут, то там либо холм, либо какое-то другое препятствие; поэтому нужно делать поправку в зависимости от высоты холма или препятствия над уровнем моря или истинным горизонтом. Только если мы все это учли, можно абсолютно точно определить склонение или расстояние от объекта до небесного экватора в момент восхода или захода. Но все-таки стоит отметить, что если достаточно лишь приближенных значений, то поправки на рефракцию и возвышенности в Северном полушарии часто компенсируют друг друга. Из-за рефракции точка восхода или захода будет казаться севернее, а из-за возвышенностей будет казаться, что небесное тело восходит или заходит южнее.

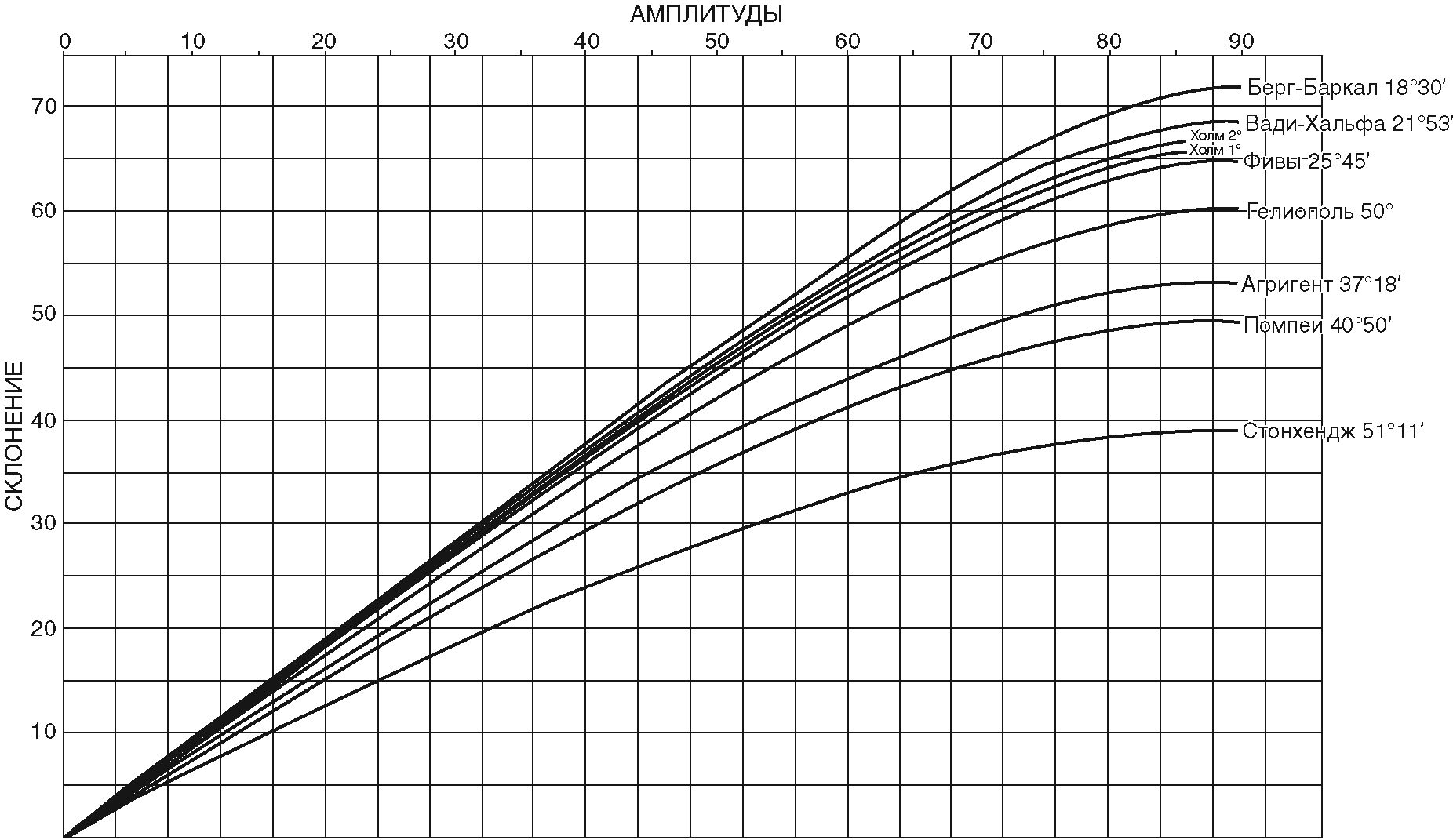
Важно подчеркнуть, что важность этих поправок может очень значительно варьироваться в зависимости от склонения рассматриваемой звезды. При высоком северном или южном склонении амплитуда увеличивается очень быстро, и чем больше она увеличивается, тем важнее становятся поправки на рефракцию и возвышение над истинным горизонтом. Во всех случаях поправку нужно рассчитывать так, чтобы амплитуда увеличивалась или уменьшалась по сравнению с истинной амплитудой вследствие рефракции в зависимости от того, где наблюдается небесное тело — Солнце или звезда — на севере или юге от экватора.

График амплитуд, с которыми звезды с разными склонениями встают и заходят на разных широтах

На графике с. 58 показаны разные амплитуды, с которыми небесные тела с разными склонениями восходят и заходят в местах с широтами от 19 до 51° с. ш. К этому графику в дальнейшем мы будем часто обращаться.