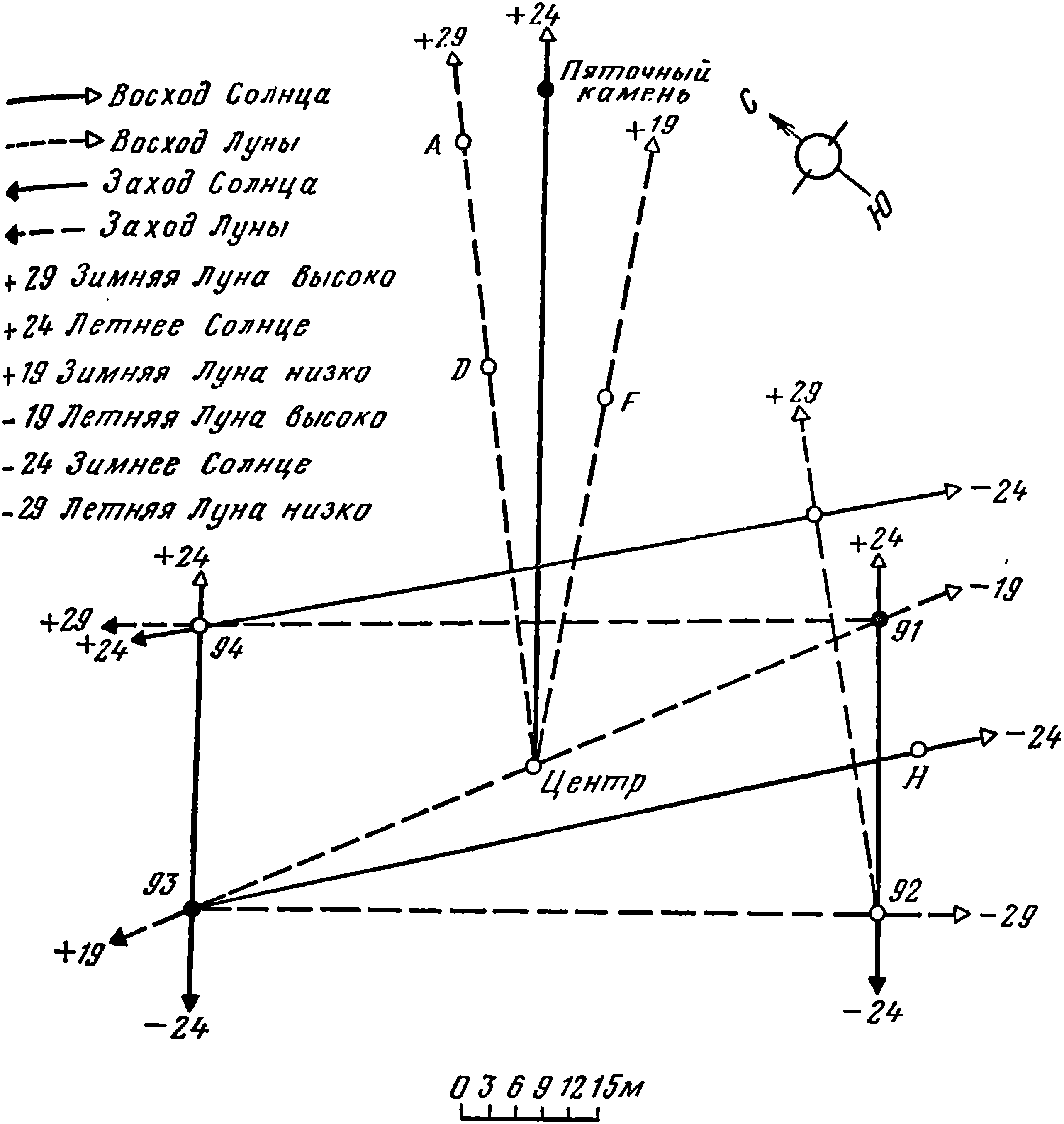
Глава 7. Электронно-вычислительная машина

Электронно-вычислительная машина — поистине нечто удивительное. Это, конечно, не техническая новинка. Уже на протяжении многих веков — с тех самых пор, как человек стал Homo sapiens, — люди прибегают к помощи разных приспособлений для облегчения счета. Сначала считали на пальцах. Потом к ним прибавились палочки, камешки, засечки и предметы, которые можно группировать и метить. А затем и более сложные устройства — песочные и водяные часы и счеты, известные уже на протяжении 2500 лет (которые в опытных руках считают быстрее, чем настольная электрическая счетная машина). В древнем Китае пользовались счетными палочками, а римляне проводили несложные расчеты с помощью камешков (по-латински — calculi). В X веке папа Сильвестр II, возможно, считался колдуном в частности потому, что научился пользоваться счетами, которые тогда были в употреблении у сарацинов. Триста лет спустя ученый монах Роджер Бэкон придумал много хитроумных машин; среди них, вероятно, были и счетные машины. Широко было распространено мнение, что у него есть какая-то медная голова, от которой он получает пророчества. В XVI веке лорд Непер, изобретатель логарифмов, по-видимому, проводил арифметические и геометрические расчеты при помощи «кусков дерева или слоновой кости с нанесенными на них цифрами, которые получили название палочек Непера».

В XVII веке искусство механического счета начало превращаться в науку. В этом же веке англичанин Уильям Отред изобрел счетную линейку. (Отред был тем самым кротким священником, у которого Кристофер Рен учился математике. Обри говорил, что Отред был «жалким проповедником», поскольку «все его мысли были сосредоточены на математике и он все время размышлял. Он чертил линии и фигуры на земле... и был весьма удачлив как астролог... его сын Бен был уверен, что отец разбирался в магии».) Француз Блез Паскаль придумал набор колес для выполнения различных арифметических действий; это было столь же ново, сколь и удобно. А немец Лейбниц создал примитивное приспособление, с помощью которого можно было производить умножение.

В конце следующего века французы пытались создать чудовищную вычислительную машину примерно из ста человек, но даже Наполеону это оказалось не под силу.

В XIX веке необыкновенно одаренный англичанин Чарлз Бэббедж, на счету которого десятки изобретений (в том числе система оплаты почтовых расходов в зависимости от веса отправления, а не от расстояния, универсальная отмычка и решетка-скотосбрасыватель на локомотивах), собрал «дифференциальную машину», при помощи которой он составил несложные математические таблицы. Он мечтал об «аналитической машине», которая могла бы производить до шестидесяти операций в минуту — неслыханная по тем временам скорость. Идею постройки такой машины поддерживали многие, например дочь Байрона Ада Августа графиня Ловлас; она была на редкость хорошим математиком. Но «аналитическая машина» так и осталась на чертежной доске. После Бэббеджа разработка вычислительных машин приостановилась; в викторианскую эпоху колеса вычислительных машин вращались вручную с приличествующей той эпохе неторопливостью.

Настоящий прогресс начался в 40-х годах нашего века. Говард Эйкен из Гарвардского университета, используя некоторые принципы старой «аналитической машины», сконструировал электромеханическую вычислительную машину с автоматическим контролем последовательности операций. Постройка его машины «Марк 1» закончилась в 1944 году. В следующем году Джон фон Нейман изобрел машинную память, и «машинная лихорадка» началась. Теперь, через какие-нибудь 20 лет, эти ранние наборы вакуумных ламп, переключателей и вспыхивающих неоновых лампочек уже сданы в музей; на смену им пришли машины с магнитной записью, работающие на транзисторах; эти машины оказывают колоссальное влияние на наше сегодня и завтра.

Современная цифровая электронно-вычислительная машина типа IBM 7090 состоит из 50 000 транзисторов, 125 000 сопротивлений и 50 000 соединений, связанных 35 километрами проводов. В более поздней модели IBM 7094 деталей примерно на 10% больше, и она работает примерно на 30% быстрее. Следующее поколение машин будет работать еще быстрее. (И, как ни странно, размеры машин уменьшаются благодаря применению транзисторов и других миниатюрных деталей и более эффективных схем). Типичная вычислительная машина состоит примерно из 20 блоков — высоких шкафов, заполненных вычисляющими и записывающими устройствами; у многих машин в верхней части, под стеклом, видны две бобины с магнитной лентой. Такая машина потребляет около 45 000 ватт электроэнергии, т. е. около 60 лошадиных сил.

Машина может выполнить в секунду до 250 000 простых операций (складывает, вычитает, находит значение тригонометрических функций и т. д.) и выдает результат со скоростью 600 печатных строк в минуту. Строки состоят из 26 пятизначных «слов», причем знаками могут быть цифры, буквы алфавита или любой другой код. Такими темпами машина могла бы «прочесть» всю Библию за минуту, а напечатать ее приблизительно за семь часов. Машина никогда не жалуется, не бывает «не в духе», не устает и, главное, не делает ошибок.

На заре машинной эры, когда использовалась модель «650», нам говорили, что некоторые небольшие ошибки объясняются «нагреванием» машины; мы верили этому и совершенно напрасно. Просто-напросто машина пыталась довести до нашего сознания, что в заложенной программе имеется существенный промах; в результате нам приходилось составлять заново всю программу. Теперь машина не только сама обнаруживает ошибку в программе, но и примерно указывает ее место и рекомендует способ устранения. Говорят, это довольно сильно нервирует начинающих программистов.

Вычислительные машины теперь используются для различных целей, в том числе для решения таких на первый взгляд далеких от математики проблем, как прогноз погоды, диагностика заболеваний, изобретательство, создание литературных произведений и перевод текстов с одного языка на другой. Машины незаменимы в космических исследованиях — без них подобные исследования были бы попросту невозможны. Вспомним, напри-мер, октябрь 1957 г., когда Советский Союз запустил первый искусственный спутник. В те дни лучшая вычислительная машина «650» работала с убогой по нынешним временам, но все же внушительной скоростью: 4000 операций в секунду, но надо было учитывать так много факторов, что машине требовалось целых 30 минут для того, чтобы вычислить орбиту спутника и не потерять его из виду. Спутник обращался вокруг Земли со скоростью около 8 километров в секунду и совершал один оборот примерно за 90 минут. Таким образом, у машины было в запасе только 60 минут. Если бы это время шло на ремонт или наладку машины, она могла бы не поспеть за спутником, и он был бы упущен. А если бы спутников было несколько, то машина «захлебнулась» бы в потоке информации. Сегодня в космосе находятся около 500 искусственных объектов, и за всеми следят усовершенствованные машины. Так называемый «космический век» можно с таким же основанием называть «веком вычислительных машин».

Современные вычислительные машины, кроме того, умеют играть. Они играют в стоклеточные шашки, в бридж, в некоторые другие не чересчур сложные игры и даже начинают играть в шахматы. (По-видимому, в скором времени, когда будут лучше разработаны программы, машины научатся играть в шахматы с чемпионами¹, и на этом все удовольствие от игры кончится, но программисты считают, что на смену нашим шахматам придет новая игра — космические шахматы для игры в трех измерениях — головоломки для программистов завтрашнего дня.) Машины способны вычислять вероятность событий. Недавно я видел кинофильм о том, как при помощи вычислительной машины удалось сорвать банк в Монте-Карло, а молодой профессор физики с самодельной вычислительной машиной чуть было на самом деле не подорвал всю систему игорных домов в Лас-Вегасе, но эта победа принесла ему поражение, так как владельцы игорных домов в панике закрыли перед ним двери своих заведений.

Наш мир превращается в мир вычислительных машин. Студентов университета загоняют в вычислительный зал в первый же год их студенческой жизни. Вычислительная машина становится неотъемлемой частью их жизни. Недавно я попросил одну студентку сделать кое-какие математические расчеты; при помощи карандаша и бумаги она справилась бы с ними часа за три. Через неделю она принесла результат, выданный машиной IBM 7090; ей пришлось прождать несколько дней, пока дошла ее очередь, чтобы использовать долю секунды машинного времени. Я с искренним недоумением спросил: «Почему вы не воспользовались арифмометром?» «Я не умею», — был ответ. «А вам не пришла мысль построить график на миллиметровой бумаге?» — «А что такое миллиметровая бумага?» Мораль этой истории, я полагаю, состоит в том, что в жизни не следует искать легких путей.

Среди поклонников вычислительных машин теперь весьма модно сравнивать возможности их кумира и человеческого мозга. Для людей выводы пока весьма утешительны: как ни хороша вычислительная машина, а человеческий мозг лучше. Подобно жерновам господним, он перемалывает информацию медленнее, чем машина, но зато очень тонко: он обладает оригинальностью и воображением, неистощимостью и свободой воли и выбора. Машина при работе использует скорости, приближающиеся к скорости света (300 000 километров в секунду), в то время как скорость работы мозга определяется скоростью распространения нервных импульсов вдоль нервных волокон, то есть примерно в миллион раз медленнее. Но машина работает линейно, то есть она посылает импульс, или «мысль», по одному пути: если этот путь оказывается тупиком, «мысль» должна вернуться назад, к последней развилке, и пойти по второму каналу, а если «мысль» сбилась с пути, весь процесс надо начать сначала. Мозг работает неким таинственным многоканальным способом, при котором мысль как бы расщепляется и движется вдоль нескольких различных путей одновременно; поэтому, что бы ни случилось с одной ветвью, на выручку ей приходят другие. И в то время как даже вычислительная машина на транзисторах собрана из сравнительно небольшого числа деталей, мозг, по-видимому, состоит из миллиардов нейронов — ячеек памяти и действия. Чтобы конкурировать со средним человеческим мозгом, вычислительная машина, построенная на уровне современной техники, должна быть размером с небоскреб или океанский лайнер. Но даже тогда ей будет недоставать оригинальности мышления и свободы воли. Чтобы машина обладала свободой выбора, оператор должен ввести в ее программу случайные числа; тогда машина будет «свободна», но не координирована, то есть станет «идиотом».

В будущем усовершенствованные машины, возможно, смогут сотрудничать с людьми в разработке более изящных программ, которые в свою очередь будут способствовать тому, что эти машины приблизятся к «мышлению» и умственным процессам и в других отношениях. Аналогии между машиной и мозгом уже проводились. В частности, указывалось², что процесс, при помощи которого машина избавляется от устаревших, повторных или иных бесполезных команд программы (то есть процесс стирания или обхода, выполняемый в то время, когда машина не занята вычислениями), аналогичен человеческим сновидениям, которые определяются как процесс, с помощью которого в нерабочее время мозг человека анализирует, упорядочивает и «раскладывает по полочкам» полезную информацию, а бесполезную — отбрасывает.

Безусловно, в будущем вычислительные машины станут не просто вспомогательным инструментом. Они будут организованы как «по вертикали» (от «роботов» общего назначения до узкоспециализированных машин), так и «по горизонтали» (по континентам и океанам). Они будут регистрировать, распределять, управлять, регулировать, решать, проектировать, предсказывать, объяснять — чего только они не будут делать!

Нетрудно представить, как машины будут исполнять некоторые функции организма, например регулировать деятельность сердца, или активность мозга, или обмен веществ. Более того, можно вообразить, что машина будет так искусно и взаимовыгодно связана с деятельностью человеческого мозга и тела, что древняя фантастическая идея о замене человека машиной найдет свое воплощение в симбиотическом союзе между машиной и человеком.

Однако довольно рассуждать о достоинствах вычислительных машин. Сам я не оператор и даже не знаю точно, как они работают. Чтобы получить ответ, я должен задавать ей вопросы через посредника-программиста. Я могу лишь сказать, что машины работают, и я этому очень рад, потому что одна из них — машина IBM 7094 (столь же устаревшая сегодня, как телефон с ручкой) помогла мне решить одну задачу, с которой я едва ли справился бы самостоятельно. Она разгадала секрет — может быть, один из секретов Стоунхенджа.

В 1961 г. я пришел к выводу, что проблема Стоунхенджа заслуживает того, чтобы призвать на помощь вычислительную машину: ввести в нее информацию, которую она может переварить, и поставить перед ней задачу, которую она может понять и решить. Машина любит точность.

Многие люди задумывались над астрономическим значением Стоунхенджа, но не могли сказать на эту тему ничего определенного.

В 1740 г. еще до написания «Choir Gaure» Джон Вуд предположил, что Стоунхендж был «храмом друидов, посвященным Луне». В 1771 г. Джон Смит отметил ориентацию сооружения на точку восхода Солнца в день летнего солнцестояния и строил догадки по поводу числа и расположения камней. В 1792 г. человек, о котором известно только, что он называл себя Уорлтайр, утверждал, что Стоунхендж представлял собой «огромный теодолит для наблюдения за движением небесных тел... и был воздвигнут по крайней мере семнадцать тысяч лет назад».

В 1793 г. преподобный Дж. Морис предположил, опираясь на мистические соображения, что Стоунхендж был храмом Солнца. В 1829 г. некий Годфри Хиггинс утверждал, что расположение камней соответствует «астрономическим циклам древности» и это позволило ему датировать постройку 4000 г. до н. э. В 40-х годах XIX века преподобный Эдвард Дьюк заметил, что линии, проходящие через «опорные» камни 91—92 и 93—94, параллельны оси Стоунхенджа и потому указывают на точку восхода Солнца в день летнего солнцестояния и на точку захода Солнца в день зимнего солнцестояния. А в 1873 г. преподобный Гидли описал метод, при помощи которого было установлено главное астрономическое направление Стоунхенджа: «Доктор Смит, не прибегая к помощи каких-либо инструментов или ассистентов, по одним лишь «эфемеридам Уайта» пришел к выводу, что в день летнего солнцестояния наблюдатель, стоящий на Алтарном камне, увидит, что Солнце восходит точно над Кланяющимся камнем». (Эфемерида, от греческого слова, означающего день или сутки, — это таблица, где даны координаты небесных тел.) Пяточный камень иногда называют Кланяющимся из-за его наклона. Со своей стороны, Гидли предположил, что «не исключено», что четыре точки, которые он не назвал (две из них были, по-видимому, насыпями у «опорных» камней 92 и 94), определяют направление на точки захода Солнца в день летнего солнцестояния и восхода Солнца в день зимнего солнцестояния. Он также отметил, что хотя «некоторые авторы» пытались связать Стоунхендж с планетами, он не обнаружил никакой «непосредственной связи с планетами, за исключением, возможно, Сатурна».

В своем труде 1880 г. Питри пришел (ошибочно) к выводу, что «опорные» камни 91 и 93 «никак не могут быть связаны с восходами или заходами в дни солнцестояний». Очень интересны его замечания о сборищах в Стоунхендже в канун дня солнцестояния, сделанные почти 100 лет назад: «Большое число людей, которые так стремятся увидеть восход Солнца в середине лета, свидетельствует о древней традиции. Это важно само по себе и, может быть, не является простым совпадением».

В XX веке высказывалось много догадок, часто весьма близких к истине, об астрономическом значении Стоунхенджа. После попытки Локьера в 1901 г. датировать время постройки памятника с помощью астрономических методов несколько видных ученых высказывали догадки о связи Стоунхенджа с астрономическими явлениями. Но их догадкам недоставало одного — точных расчетов. Такие теории следует проверять математически. Только цифры могут вдохнуть жизнь в теорию, а в случае неудачи — убить ее.

Электронно-вычислительной машине я должен был дать конкретный материал: максимально точные данные и четко сформулированную задачу. Только при этих условиях можно было получить ответ на заданный вопрос. Мой вопрос был достаточно четким: совпадают ли важнейшие направления Стоунхенджа с важнейшими направлениями на небесной сфере. Понятие «важнейшие» для Стоунхенджа и для небесной сферы представлялось очевидным. В Стоунхедже так много направлений (27 060 направлений, определяемых попарно 165 точками), что любое из них указывает на какое-нибудь светило на небесной сфере, и наоборот, небесных тел так много — буквально бесчисленное множество, что любая линия, проведенная на Земле, непременно укажет на какое-нибудь из них.

Чтобы ответить на заданный вопрос, машине требовалась соответствующая информация о Стоунхендже и небесной сфере, и мы начали давать ей эту информацию.

Прежде всего, программисты Шошана Розенталь и Джули Коул (позднее к нам присоединилась Джуди Копленд) взяли карту Стоунхенджа, на которой было отмечено 165 пунктов (камни, лунки от камней, прочие лунки, насыпи), и поместили ее в автоматическую измерительную машину «Оскар»³. Затем они наводили крест нитей на все отмеченные пункты и особые геометрические точки (например, на центр камня или лунки и на середину арки), нажимали на кнопку и «Оскар» пробивал на перфокарте координаты каждой точки. Точка начала отсчета координат была выбрана произвольно за пределами изучаемой области в юго-западном квадранте, чтобы все координаты были положительными.

Затем перешли к вычислительной машине. Ей сообщили географические сведения (широту и долготу выбранной точки начала координат, ориентацию осей относительно стран света и масштаб) и дали команду выполнить три операции:

1) провести прямые через 120 пар нанесенных на карту точек (некоторые пары — например соседние точки — были сочтены бесполезными для этой цели);

2) определить направления (азимуты) этих линий;

3) определить склонения точек на небесной сфере, в которые «упираются» эти линии. (Если считать, что все небесные тела лежат на полой сфере, в центре которой находится Земля, то окружности на этой сфере, соответствующие земным параллелям, называются суточными параллелями светил, а их расстояние от небесного экватора, соответствующего земному экватору, называется склонением светила.)

Надеюсь, это понятно. Для ясности можно сказать так: машину как бы просили встать в каждую намеченную точку, посмотреть в направлении всех остальных точек на горизонт и сказать, какую точку на небе — с каким склонением — она видит.

Этот подготовительный процесс — программирование машины — занял почти день. Затем перфокарты «Оскара» были переданы оператору, который ввел их в машину. Через несколько секунд машина перевела информацию с перфокарт на магнитную ленту, прочитала ленту, обработала информацию в соответствии с запрограммированными командами и выдала результат — 240 направлений Стоунхенджа были переведены в значения склонений (120 пар точек задают в два раза больше направлений, так как каждая прямая задает два направления).

На все это потребовалось меньше одной минуты машинного времени. Вычислитель занимался бы этим делом месяца четыре. (Для проверки Ш. Розенталь выполнила один расчет вручную. На это ушло четыре часа.)

Таким образом, задача была наполовину решена. Мы узнали склонения тех точек, на которые указывают важнейшие направления Стоунхенджа. Оставалось еще выяснить, имеют ли эти склонения астрономическое значение, т. е. соответствуют ли они точкам восхода или захода некоторых небесных тел.

Мы сразу же заметили, что среди значений склонений, выданных машиной, было много одинаковых. Часто попадались числа, близкие к +29°, +24° и +19° (плюс означает северное склонение), и их южные двойники: −29°, −24° и −19°. Мы решили выяснить, какие небесные тела имеют такие склонения.

Сначала мы проверили планеты. Больше всего подходила Венера, но ее крайние склонения (±32°) были великоваты. Почему Гидли считал, что Стоунхендж как-то связан с Сатурном, я не знаю: его крайние склонения равны ±26° и в 1500 г. до н. э. были примерно такими же.

Затем мы пробежались по звездам (лихо звучит!). Шесть самых ярких звезд (в порядке убывания яркости) следующие: Сириус, Канопус, Альфа Центавра, Вега, Капелла и Арктур. Из них только склонение ярчайшей — Сириуса — приближалось к нужному значению. Сейчас склонение Сириуса равно — 1639′, но в 1500 г. до н. э. оно было равно −18°. Как установил Локьер, скорость изменения склонения у разных звезд различна: она зависит как от их истинного движения, называемого собственным движением, так и от движения земной оси. Сейчас склонение Арктура составляет +19°21′, но в 1500 г. до н. э. оно было равно +40°, т. е. даже близко не подходило к линиям Стоунхенджа. Таким образом, никакой связи со звездами не обнаружилось, но даже если бы оказалось, что когда-то в прошлом у Сириуса или у нескольких более слабых звезд было подходящее склонение, это было бы чистой случайностью и не меняло бы дела. Ведь восход даже такой яркой звезды, как Сириус, можно наблюдать только при особо благоприятной погоде. Более слабые звезды вообще не видны близ горизонта. Мы решили проверить наиболее очевидные небесные объекты, которые в доисторические времена считались божествами, — Солнце и Луну.

На этот раз результаты были поразительные. Склонения, вычисленные машиной, настойчиво и строго повторяли крайние положения Солнца (что я ожидал) и Луны (чего я не ожидал). Пара за парой точки Стоунхенджа, по-видимому, указывали на крайние склонения двух самых ярких небесных светил.

Я говорю «по-видимому», потому что в то время мы пользовались предварительной, поисковой программой, дававшей малую точность. Направления, определяемые камнями, и результирующие склонения определялись со всей точностью, которую допускала первоначальная карта, но в то время мы не располагали точными склонениями Солнца и Луны для эпохи сооружения Стоунхенджа. Мы пользовались только приближенными значениями, мысленно проследив эти объекты на 4000 лет назад. Чтобы подтвердить это совпадение, нам нужны были точные значения крайних склонений Солнца и Луны в 1500 г. до н. э.

Конечно, пришлось снова прибегнуть к помощи машины. Мы задали ей современные крайние склонения Солнца и Луны и скорость их изменения и приказали ей определить крайние склонения в 1500 г. до н. э. Одновременно машина должна была рассчитать направления точек восхода и захода Солнца и Луны. Не зная, из чего исходили строители Стоунхенджа, мы учли три случая: а) диск Солнца только показывается над горизонтом; б) половина диска поднялась над горизонтом; в) нижняя точка диска касается линии горизонта. Между положениями а) и в) разница составляет примерно 1°; это, конечно, немного, но мне хотелось выяснить, что предпочитали строители.

Настало время испытать терпение читателя и изложить некоторые сведения из астрономии. Я должен сделать кое-какие разъяснения относительно Луны.

Как я говорил, склонение Солнца меняется от +23,5° летом до −23,5° зимой. Для Луны в полнолуние справедливо обратное. Она движется на север зимой и на юг летом, но ее относительное движение гораздо сложнее, чем у Солнца: у нее два северных и два южных крайних положения. В течение цикла, продолжающегося 18,61 года, Луна движется таким образом, что ее крайние северные и южные склонения перемещаются с 29° до 19° и обратно до 29°, т. е. в ее движении имеются два крайних положения в северном и южном полушариях неба: ±29° и ±19°. Это маятникообразное движение вызвано совокупным действием наклона плоскости орбиты Луны и прецессии и слишком сложно, чтобы его можно было объяснить в двух словах. Даже астроному нелегко это себе представить. Здесь же требуется только запомнить, что на одно крайнее положение Солнца приходится два крайних положения Луны.

Машине потребовалось еще несколько секунд, чтобы определить крайние склонения Солнца и Луны в 1500 г. до н. э. Ответ был такой: ±23,9° для Солнца и ±29,0° и ±18,7° для Луны. С первого взгляда стало ясно, что эти значения близки, даже очень близки к значениям, полученным для Стоунхенджа.

Рис. 11. Первоначальные направления, определенные по Стоунхенджу I. Точные значения азимутов приведены в табл. 1

Мы тщательно сравнили все числа. Сомнений не было. Основные и часто повторяющиеся направления Стоунхенджа указывали на Солнце и Луну.

Как я уже говорил, я ожидал некоторой корреляции, но я не был подготовлен к полному совпадению результатов для Солнца, и для меня было большой неожиданностью существование почти полного совпадения для Луны. Ибо расчеты машины показали, что:

1) со средней точностью выше 1° двенадцать важных направлений Стоунхенджа указывали на крайние положения Солнца и

2) со средней точностью около 1,5° двенадцать направлений указывали на крайние положения Луны.

Как показывают диаграммы на рис. 11 и 12, а также табл. 1, все прямые, соединяющие все основные пункты Стоунхенджа, непременно указывают на какое-нибудь особое положение Солнца или Луны. Очень часто на одной прямой, соединяющей два важных пункта, находится и третий объект — добавочный ориентир. И из 12 точек, задающих направления на крайние положения восходов и заходов Солнца и Луны, только две — точки захода Луны в летнее солнцестояние (−29° и −19°) — не обладают таким дополнительным ориентиром⁴.

Соотношение между ошибкой по вертикали и соответствующей ошибкой по горизонтали меняется в зависимости от величины склонения. При склонении ±29° ошибка по вертикали в 1° означает ошибку по горизонтали в 1,8°; при склонении ±24° отношение ошибок равно 1:1,6; при склонении ±19° оно равно 1:1,5; при склонении ±5° оно равно 1:1,3, а при склонении 0° оно равно 1:1,2.

Можно заметить, что эти значения несколько отличаются от приведенных в статье «Разгадка Стоунхенджа» (приложение А). Это произошло потому, что в результате проверки машинной программы (после выхода в свет статьи) некоторые результаты были уточнены и добавилось четыре направления: три положения Солнца (91 из 92, G из 94 и 93 из 94) и точка восхода Луны в день зимнего солнцестояния (G из 92).

Таблица 1

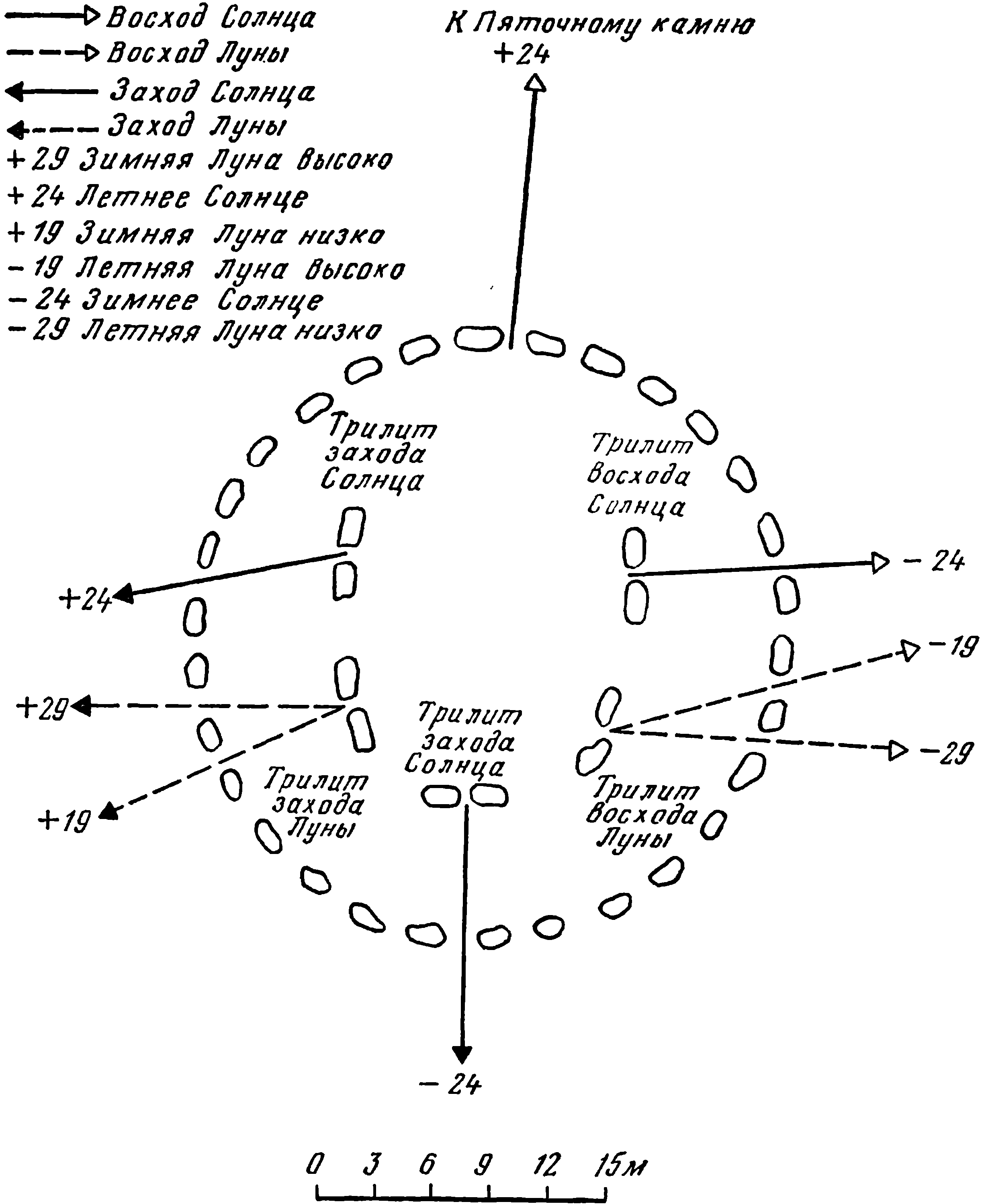
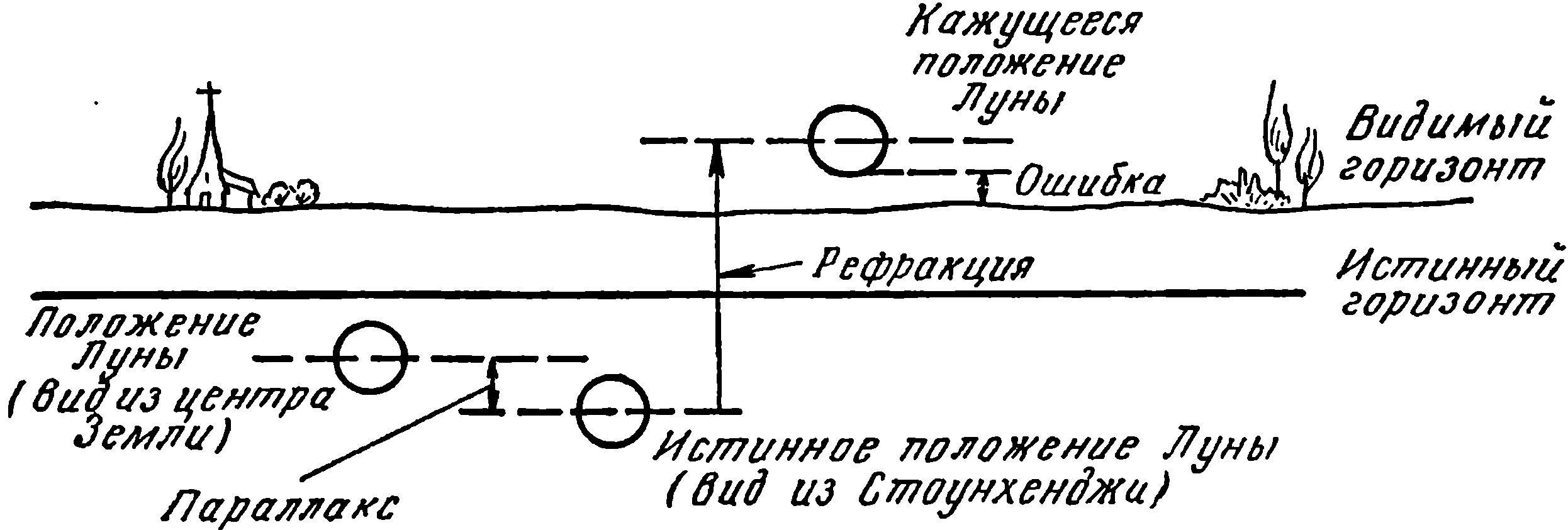
Совпадение направлений было примечательным. Точнее всего направления совпадали в предположении, что моментом восхода строители Стоунхенджа считали момент, когда Солнце и Луна касаются линии горизонта нижней точкой диска. Как показывает таблица, средняя точность направлений, связанных с Солнцем, составляла 0,8°, а направлений, связанных с Луной, 1,5°. Эти средние ошибки вызваны в большой степени двумя «плохими» арками в западной стороне, установленными с ошибками 3,2° и 5,4°. Ошибка приведена в последнем столбце таблицы и показана схематически на рис. 13. Из-за наклонного направления движения Солнца при восходе ошибка в 1° по вертикали соответствует ошибке 1,6° по горизонтали при склонении 24°.

Ученые, как правило, не обсуждают ошибок. После того как приняты все меры предосторожности, ошибку регистрируют и все, потому что при повторной обработке данных ошибка может уменьшиться, а при третьей обработке — опять возрасти. Ошибки остаются ошибками.

Но в случае Стоунхенджа такая работа могла оказаться поучительной. Отметим прежде всего, что числа в табл. 1 и в таблице, приведенной в приложении А, несколько различаются. Это объясняется тем, что во время написания статьи для журнала «Нейчер» я не располагал сведениями о фактическом профиле линии видимого горизонта вокруг Стоунхенджа и исходил из предположения о ровной линии горизонта. Позднее я достал карту, где были нанесены фактические высоты. Поэтому табл. 1 дает более точные значения. Однако ниоткуда не следует, что в 1500 г. до н. э. линия видимого горизонта совпадала с теперешней или была идеально ровной. Деревья, которые росли в тех местах, где сейчас нет ничего, могли поднять линию видимого горизонта на 0,2°, т. е. то, что мы считаем ошибкой +0,2°, тогда могло быть равно нулю.

Во-вторых, мы обнаружили, что топографические карты Стоунхенджа различаются между собой, и мы не знали, которой из них отдать предпочтение. Это дает дополнительную ошибку в каждом значении ±0,2°. Ошибка в направлении линии 94—G может колебаться от 0,1 до 0,5°. Это неприятно, но не имеет большого значения, так как даже 5° — малая погрешность при наблюдении невооруженным глазом.

В-третьих, некоторая ошибка могла возникнуть, когда жрецы размечали направления. Солнце можно было наблюдать в течение нескольких критических дней в периоды зимнего и летнего солнцестояний, поэтому ошибка будет невелика. Но полную Луну надо было наблюдать именно в ночь полнолуния в определенный год 19-летнего цикла. Если небо тогда было затянуто облаками и направления были определены накануне или на следующую ночь, положение Луны было бы отмечено не совсем точно. В этом случае ошибка была положительной при положительном склонении Луны и отрицательной — при отрицательном склонении. Из табл. 1 сразу видно, что эти (+) и (−) встречаются в 10 лунных случаях из 12. По-видимому, не всегда у них погода была ясной!

Рис. 12. Направления, определяемые арками Стоунхенджа III. Точные значения азимутов приведены в табл. 1

В-четвертых, Стоунхендж уже не тот, что был ранее. Некоторые камни опрокинулись и разбились на куски, другие были поставлены на место при помощи современных подъемных кранов. Самые большие ошибки связаны с теми пунктами, откуда камни исчезли давным-давно: это пункты № 24, 15 и 20. Их первоначальное положение можно было установить лишь приближенно. Может быть, нам не следует вычислять для них ошибки, пока в этих местах не поработают археологи. Имеется ли лунка под слоем почвы близ предполагаемого места и не смещена ли эта лунка на несколько десятков сантиметров в сторону? Далее, возможно также, что в точках № 24, 15 и 20 вообще не было установлено камней, так как строители Стоунхенджа сообразили, что абсолютно симметричное сооружение не подходит для асимметричного расположения небесных светил.

Наконец, самой главной причиной ошибок может быть человек наших дней. Обратите внимание, какими плоскими кажутся арки 57—58, 21—22, отмечающие заход Луны, на аэрофотоснимке 1944 г. Они упали в 1798 г. до того, как были точно измерены. В 1958 г. Министерство гражданского строительства установило их вертикально, но первоначально эти камни стояли в неглубоких лунках и было трудно вернуть их точно на старое место. Из моих расчетов следует, что одна из двух арок установлена с ошибкой в 40 сантиметров; возможно, эта ошибка возникла при реставрации.

Трилиты захода Солнца также находятся сейчас в жалком состоянии. Большой трилит упал несколько сотен лет назад и разбился. Хотя камень 56 был снова установлен в 1901 г., многие авторы высказывали сомнения в точности реставрационных работ: камень не перпендикулярен оси Стоунхенджа, а повернут на несколько градусов против часовой стрелки. Трилит захода Солнца в день летнего солнцестояния сильно накренился, а соответствующая арка № 23 в высшей степени ненадежна, Камень 23 упал, был поднят, снова упал и наконец в 1964 г. был водворен на место и зацементирован.

Чтобы убедиться в справедливости моего предположения о недавнем происхождении некоторых ошибок, достаточно вспомнить, что трилиты и арки, которые ни разу не падали, стоят гораздо точнее.

Особенно следует проанализировать ошибку самого главного направления из всех — направления на точку восхода Солнца в день летнего солнцестояния над Пяточным камнем. В настоящее время человек ростом 183 сантиметра, стоящий в центре, видит вершину Пяточного камня точно на уровне горизонта. В 1800 г. до н. э. первый солнечный луч появлялся на ¾ градуса севернее (то есть левее), так что человек ростом 183 сантиметра, стоящий в центре, увидел бы нижний край Солнца на высоте 0,5° над вершиной Пяточного камня при условии, что угол наклона этого камня в то время был таким же, как сегодня. Но если в 1800 г. до н. э. камень стоял вертикально (а я думаю, что так оно и было), то он был сантиметров на 50 выше, чем теперь, то есть вычисленная машиной для теперешнего положения ошибка в 0,5° тогда была практически равна нулю.

Рис. 13. Условия при восходе или заходе. Сначала астрономические вычисления проводятся для наблюдателя в центре Земли. Чтобы рассчитать условия для наблюдателя на поверхности Земли, надо ввести поправку на параллакс. Затем надо учесть атмосферную рефракцию, из-за которой светило кажется выше над горизонтом, чем на самом деле. Наконец, надо принять во внимание высоту видимого горизонта, который, как правило, бывает выше астрономического горизонта, определяемого горизонтальной плоскостью, находящейся на уровне глаз наблюдателя

Я вычислял табл. 1 в предположении, что Пяточный камень стоял вертикально, то есть наблюдатель в каменном веке видел, что диск Солнца чуть-чуть выглядывал над верхним краем камня по мере того, как Солнце всходило и проходило за камнем. В данном случае нет никаких сомнений в том, что строители Стоунхенджа хотели установить отметку так, чтобы диск Солнца лежал прямо на его вершине.

Такая точность ориентации поразительна. Установка громадного камня такой неправильной формы, как Пяточный камень, весящий 35 тонн, на верной горизонтальной прямой с точностью до 30 сантиметров была достаточно сложным делом. Затем надо было погрузить эту огромную каменную глыбу в грунт ровно настолько (не более и не менее), чтобы ее вершина оказалась на нужной высоте с точностью до нескольких сантиметров; это достижение, требующее особых знаний и навыков. Как же это было сделано? Если бы после установки камень осел слишком сильно и его вершина оказалась бы не на линии, то как удалось бы его приподнять? Конечно, если камень осядет недостаточно, верхнюю его часть можно немного сколоть, но у Пяточного камня она не сколота. Может быть, Пяточный камень был установлен в первую очередь, а по нему уже был выбран центр?

Но довольно об ошибках.

Наконец, следует отметить, что на протяжении всех этапов строительства необходимые направления бережно сохранялись и дополнялись, а вид всего сооружения становился все более внушительным. В течение 300 лет строительства Стоунхенджем занималось много людей с различным образом мышления и уровнем культуры. Много разных правителей, зодчих, жрецов и рабочих участвовали в планировании, строительстве, усовершенствовании, уточнении и дополнении этого ансамбля. Это монументальное сооружение, возникшее как простое кольцо, разорванное в направлении восхода Солнца в день летнего солнцестояния, превратилось в прямоугольник, вписанный в окружность, и в массивный «храм» сложной конструкции из камней, установленных в форме подков и колец из арок. Однако самая древняя ориентация (на точку восхода Солнца в день летнего солнцестояния) не была утеряна; наоборот, ее сохранили, многократно продублировали и выделили среди прочих направлений. Аналогичным образом были сохранены, продублированы и сделаны более подчеркнутыми и другие направления. И точно так же, как первые строители использовали каждый важный камень для дублирования направления на Солнце и Луну, строители, пришедшие им на смену, располагали свои кольца и подковы столь искусно, что каждая гигантская арка трилита вместе с одной из арок внешнего кольца обязательно давала направление на одно из крайних положений Солнца или Луны.

Работа, проведенная первыми строителями, замечательна сама по себе: совсем не просто расположить окружность, прямоугольник и шесть внешних камней таким образом, чтобы попарно они определяли 16 направлений на 10 (из 12) особых положений Солнца и Луны. А то, что сделали последние строители, еще более замечательно: они установили каменные арки таким образом, чтобы продублировать 8 из этих направлений. В то время как строители Стоунхенджа I и II получали нужное направление, стоя в одной точке и глядя поверх другой, строители Стоунхенджа III могли наблюдать 8 восходов и заходов Солнца и Луны в определенные дни сквозь высокие каменные арки. Последние строители, подобно первым, использовали один объект для проведения нескольких направлений. Посмотрите, как два трилита, которые я на рис. 12 назвал трилитами восхода и захода Луны, вместе с двумя арками сарсенового кольца задают четыре направления.

Последние строители не только установили свои гигантские камни в точном соответствии с астрономическими направлениями, но расположили их таким образом, чтобы не нарушить уже имевшиеся направления, хотя их камни дублировали эти же первоначальные прямые. Для радиуса своего сарсенового кольца они выбрали такое расстояние, чтобы северо-восточный и юго-западный камни этого кольца не стояли на пути старых лучей зрения 91—94 и 92—93⁵. При сооружении внутреннего кольца и подковы Стоунхенджа III из 16 направлений Стоунхенджа I и II было сохранено 11 (кроме линий центр—91, центр—93, центр—A, центр—D и 98—H). Строители очень искусно сохранили и продублировали направления, определяемые прямоугольной конфигурацией (осью Стоунхенджа I и II и «опорными» камнями), при помощи двух кривых — сарсенового кольца Стоунхенджа III и трилитовой подковы.

Для создания такого мегалитического храма Солнца и Луны в его окончательном виде требовалось совершенно необыкновенное сочетание теоретических и инженерных способностей с мастерством строителей. Вдумайтесь в задачу, которую они перед собой поставили: спроектировать и построить окружность, включающую в себя подкову таким образом, чтобы все элементы обеих фигур находились друг от друга на одинаковых расстояниях и при этом расположены так, что 5 узких арок подковы вместе с 7 узкими арками окружности определяли направления на 7 из 12 крайних положений Солнца и Луны на горизонте, в то время как ось всего сооружения, проходя через еще одну арку окружности, указывает на восьмую точку на небе. Все это приходилось делать с помощью примитивных инструментов, используя в качестве «элементов» гигантские каменные монолиты весом в 30 тонн и более. Сегодня мы видим, насколько они преуспели в задуманном предприятии.

Строителям Стоунхенджа I (вернее сказать, его первым зодчим и подчиненным им группам рабочих, ибо совершенно очевидно, что до начала работ все сооружение было тщательно распланировано на местности) для его создания требовалась не только физическая сила и ремесленная сноровка, но и знания, целеустремленность и терпение. Для строительства Стоунхенджа II требовалось еще больше знаний и такая же целеустремленность. Для завершения этого величественного сооружения, представляющего единое целое — монументальный храм со сложной системой направлений, скрытой за кажущейся простотой и симметричностью, — требовались еще больший объем знаний и единая цель, к осуществлению которой на протяжении 300 лет шли различные народы с разной культурой и обычаями и умевшие делать то, чего не могут многие наши современники.

Взгляните на рисунки еще раз. Обратите внимание на экономичность конструкции, на то, как одна точка используется для определения нескольких направлений.

В Стоунхендже I восемь пар точек задают направления на Солнце и восемь — на Луну; всего 16 направлений, определяемых двумя точками каждое. И тем не менее использованы не 32 точки, а только 11, причем 6 точек использовано более одного раза, из них 2 точки — по 6 раз каждая.

Теперь посмотрите на линии Стоунхенджа III. Там появилось еще четыре направления на Солнце и еще четыре — на Луну благодаря двукратному использованию каждого «лунного» трилита. Хотелось бы подчеркнуть, что эти линии зрения, проходящие через трилиты сарсенового кольца, не были произвольно выбраны для астрономических целей из множества возможных линий. Если вы, подобно мне, встанете в эту подкову и захотите посмотреть сквозь арки в направлениях, отличных от указанных на плане, то вы, как и я, обнаружите, что сделать это невозможно. Ваше поле зрения будет ограничено малой шириной щелей. В направлениях, которые не указывают на особые положения Солнца и Луны, ничего не видно; вы волей-неволей смотрите через спаренные арки в направлении крайних положений Солнца и Луны. Более того, я считаю, что выемки в вертикальных камнях трилитов — вовсе не результат выветривания, как неоднократно писали ранее, а вырублены специально, чтобы там могла поместиться голова человека, когда требуется посмотреть в сторону.

Подводя итоги, можно сказать, что в Стоунхендже I имеется 11 ключевых точек; каждая точка в паре с другой (а иногда более чем с одной точкой) задают 16 направлений на 10 из 12 крайних положений Солнца и Луны. В Стоунхендже III направления, определяемые пятью трилитами и Пяточным камнем, восемь раз указывают на восемь из этих крайних положений.

Такая корреляция не может быть случайной. После того как машина установила, что строители Стоунхенджа сориентировали свое сооружение по Солнцу и Луне с таким искусством, последовательностью и ценой такого труда, естественно возник вопрос: «Зачем?». Во имя чего затрачено столько усилий?

Ведь для того, чтобы отметить точку восхода Солнца (или любую другую точку на небесной сфере), достаточно двух камней. Так зачем же строителям Стоунхенджа понадобилось такое множество направлений?

Только археологи и историки смогут когда-нибудь ответить на этот вопрос. Мы, астрономы, с нашими вычислительными машинами можем лишь поставлять специалистам по древним культурам фактический материал для размышлений.

Но мне хотелось бы высказать свои соображения.

Солнечно-лунные направления в Стоунхендже были установлены и отмечены по двум, а возможно, и по трем причинам: они служили календарем, особенно полезным для предсказания времени начала сева: они способствовали установлению и сохранению власти жрецов, так как позволяли жрецам устраивать театрализованное представление по наблюдению восходов и заходов Солнца и Луны, особенно восхода Солнца над Пяточным камнем в день летнего солнцестояния и захода Солнца в арке большого трилита в день зимнего солнцестояния; возможно, они служили также для чисто интеллектуальных упражнений.

Говоря об этих трех причинах подробнее, я хотел бы указать, что, как хорошо известно, умение определить время начала сева имело жизненно важное значение для первобытного человека. Это время трудно установить. Невозможно отсчитывать время назад от теплых летних дней; нужен какой-то иной способ. А что может быть удобнее для определения смены времен года, чем наблюдения за регулярными и предсказуемыми движениями небесных тел? Даже еще в античности существовал тщательно разработанный свод правил, помогавших крестьянам определить время наступления периода сева по небесным явлениям. Обсуждая «глубокий вопрос» о «времени, надлежащем для сева», Плиний писал, что этим надо заниматься чрезвычайно осторожно и осмотрительно, полагаясь в основном на астрономию. Несомненно, еще и в наши дни есть земледельцы, которые прибегают к этому методу.

Что же касается возможного значения Стоунхенджа для приумножения власти жрецов, то представляется весьма вероятным, что на человека, который мог созвать людей, чтобы продемонстрировать им появление или исчезновение божества, олицетворяющего день или ночь, точно в указанном месте, за одной из этих внушительных арок, на такого человека распространялся ореол божественности. Вероятно, обладание таким чудесным храмом возвышало весь народ в его собственных глазах.

Еще одно вероятное объяснение астрономического хитроумия Стоунхенджа принадлежит лично мне. Я думаю, что строители Стоунхенджа были нашими истинными предками. Я думаю, что люди, которые проектировали его различные части, и, возможно, некоторые строители получали истинное удовольствие от «умственной гимнастики», выходившей далеко за пределы их прямых обязанностей. Я думаю, что когда при постройке Стоунхенджа I они решили основную проблему эффективно, но не эффектно, они не могли с этим примириться и на этом успокоиться. Они поставили перед собой новые задачи, еще более сложные, в поисках новых, еще более внушительных решений отчасти для прославления бога, но отчасти и для удовольствия человека — мыслящего существа. Быть может, наступит день, когда какой-нибудь ученый установит связь между духовными устремлениями строителей Стоунхенджа и создателей Парфенона, готических соборов и первого космического корабля.

Во всяком случае, какими бы мотивами ни руководствовались строители Стоунхенджа, их детище оказалось чудом. Столь же сложный, как целый комплекс астрономических инструментов, и в то же время идеально простой с архитектурной точки зрения, тонкий и сложный по своим функциям, по виду экономичный и грандиозный, внушающий трепет Стоунхендж являет собой немеркнущий образец гениального замысла, разнообразного назначения и величия. По замыслу и выполнению — это восьмое чудо древнего мира.

Известно семь классических чудес света: пирамиды в Египте (или одна Великая пирамида), «висячие сады Семирамиды» в Вавилоне, статуя Зевса в Олимпии, храм Дианы в Эфесе, мавзолей в Галикарнассе, Колосс Родосский и Александрийский маяк на острове Фарос. За исключением наиболее недолговечных частей вавилонских садов и Колосса (предполагается, что это была медная фигура высотой около 85 метров), все эти чудеса были сделаны из камня. Но ни в одном из них сам камень не был использован столь искусно для увековечения плодов интеллектуального дерзания, как в потрясающем воображение храме на Солсберийской равнине.

Примечания

*. Угол (в градусах), отсчитываемый от точки севера вдоль горизонта по часовой стрелке.

**. Положение самой нижней точки Солнца или Луны над (+) или под (−) линией горизонта в данном азимуте. Нуль означает, что Солнце или Луна касались линии горизонта самой нижней точкой диска, как колесо касается земли.

***. На сегодняшний день в Стоунхендже нет этих лунок от камней, и они не отмечены ни на одной схеме раскопок. Положения средних точек этих арок определены по симметричному расположению соседних объектов.

****. На сегодняшний день в Стоунхендже нет этих лунок от камней, и они не отмечены ни на одной схеме раскопок. Положения средних точек этих арок определены по симметричному расположению соседних объектов.

1. Лет десять тому назад эта идея действительно казалась недалекой от реализации, однако и поныне машины в силах состязаться лишь с шахматистами средней руки; таким образом, потери интереса к шахматной игре от вмешательства машины в обозримом будущем не предвидится. — Прим. ред.

2. C.R. Evans, E.A. Newman. New Scientist, November 26. 1964.

3. Большинству машин присваивается номер или имя по фамилии изобретателя или мифических персонажей (вроде «Юпитер» или «Тор»), но как появилось имя «Оскар» — никто не знает.

4. Камни, которые дополнили бы эти два направления, должны были бы находиться (из соображений симметрии) близ лунки Обри № 28, но в этом районе тщательных раскопок еще не проводилось.

5. Тот факт, что сарсеновое кольцо вписано в прямоугольник, составленный из «опорных» камней, был замечен уже давно; это считалось случайным совпадением или одной из неразрешенных загадок Стоунхенджа. Открытие солнечно-лунной ориентации ясно показывает, что строители Стоунхенджа III, которые так тщательно прокладывали свои собственные направления, столь же бережно относились к более древним вехам; при постройке своего большого кольца они учитывали не только их направления, но и размеры.