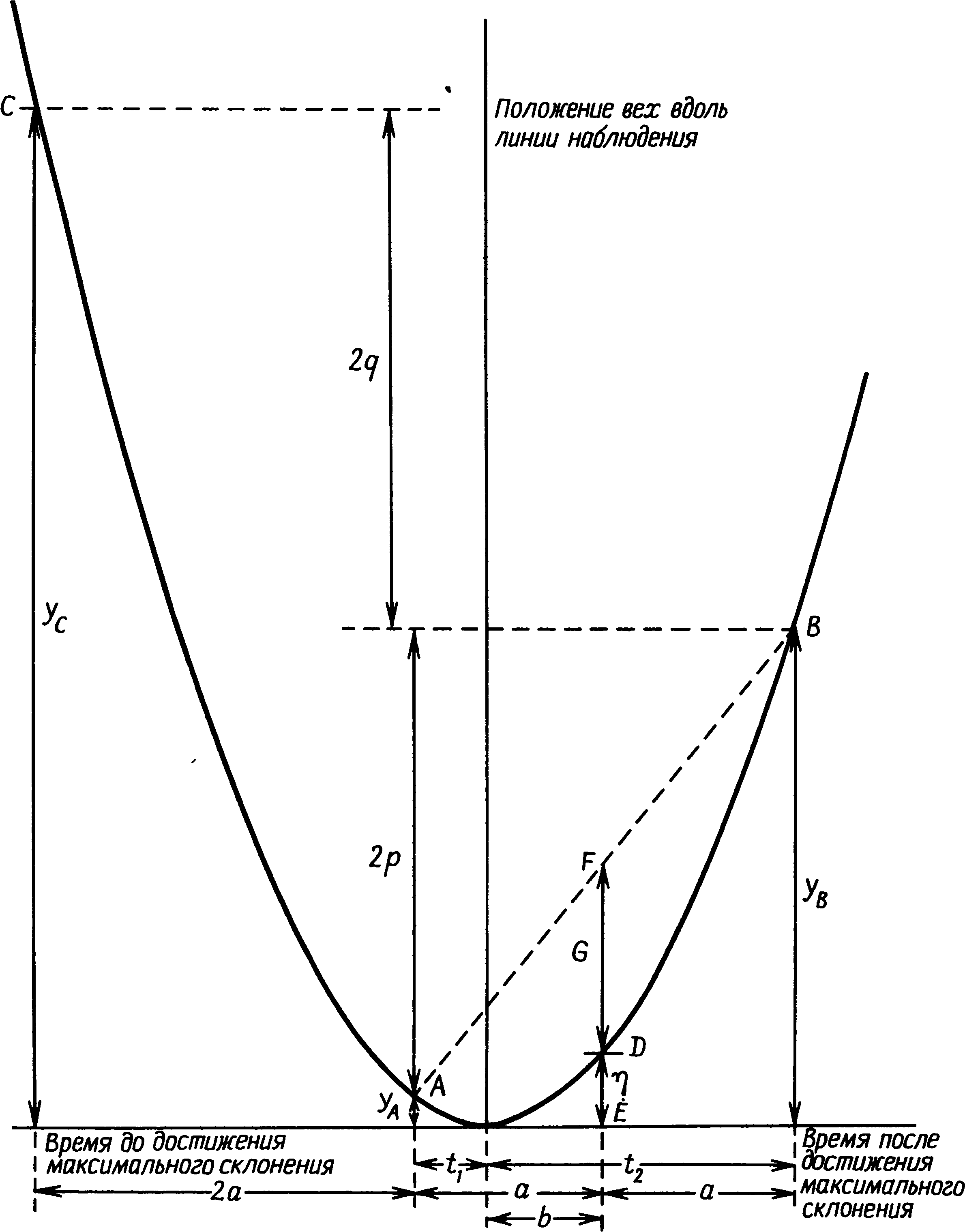
Приложение А. Математические доказательства

Вывод экстраполируемого расстояния

Здесь приводится вывод величины η, используемой в гл. 7 (стр. 159). Рис. А.1 в общих чертах совпадает с рис. 7.3, на нем показано положение кольев в зависимости от времени до и после наибольшего склонения. На рисунке отмечено положение кольев A и B в моменты t₁ и t₂ соответственно до и после момента наибольшего склонения, находящихся на расстояниях y_A и y_B от положения кола, соответствующего наибольшему склонению. Заметим, что расстояния y_A и y_B нам не известны, и мы знаем только разность этих расстояний, равную 2p.

Введем неизвестную постоянную k для описания параболы уравнением y = kt². Примем также t₁ = a − b и t₂ = a + b. Тогда

y_B = kt²₂ = k (a + b)² = ka² + kb² + 2kab, (1)

y_A = kt²₁ = k (a − b)² = ka² + kb² − 2kab. (2)

Вычитая одно выражение из другого, получаем y_B − y_A = 4kab, но эта величина равна также 2p, откуда

k = p/2ab. (3)

Аналогично

η = ED = kb². (4)

Полное расстояние, которое надо отложить от середины между двумя кольями, G + η равно (y_A + y_B)/2, для которого путем сложения (1) и (2) получаем k (a² + b²). Используя уравнение (4), находим G = ka².

Пусть a равно половине суток, тогда G будет равно расстоянию между положением кола, отмечающего наибольшее склонение, и положением кольев, поставленных точно за полсуток до и после момента наибольшего склонения. Исключая k с помощью уравнения (3), получаем

G = ka² = ap/(2b) = p(a/b)/2,

η = kb² = bp/(2a) = p(b/a)/2,

Рис. А.1. Положение вех в зависимости от времени до и после наибольшего склонения Луны

откуда

η = p²/(4G).

Итак, полное расстояние, которое надо отложить от середины между двумя кольями, равно G + (p²/4G), откуда следует, что расстояние, которое следует отложить от дальнего кола, составляет

G + (p²/4G) − p.

Экстраполяция по результатам наблюдений три ночи подряд

Экстраполяция по результатам наблюдений Луны три ночи подряд — это метод, возможно, использовавшийся в Бретани (гл. 8). На рис. А.1 показаны положения кольев C, A и B, поставленных за время 2a + t₁ и t₁ до момента наибольшего склонения и через 2a − t₁ после этого момента. Расстояния y_C, y_A и y_B — это расстояния, отделяющие указанные колья от места кола, соответствующего наибольшему склонению. Заметим, что расстояния эти нам не известны, и мы знаем только разделяющие перечисленные колья расстояния 2p и 2q.

Используя для описания параболы ту же постоянную k, что и при рассмотрении метода двух ночей, имеем

y_A = kt₁²,

y_B = k(2a − t₁)² = k (4a² + t₁² − 4at₁),

y_C = k(2a + t₁)² = k (4a² + t₁² + 4at₁).

Путем вычитания получаем

2q = y_C − y_B = 8kat₁,

откуда

q = 4kat₁ и k = q/(4at₁).

Из предыдущего доказательства в этом приложении мы знаем, что G = ka². Тогда

G = qa²/(4at₁) и t₁/a = q/(4G).

Но

y_A = kt² = qt₁²(4at₁) = (q/4)(t₁/a), откуда

y_A = q²/(16G).

В гл. 8 для обозначения расстояния, которое следует отложить от дальнего кола, вместо символа y_A использовался символ η′. Следует указать, что эти обозначения отличаются от тех, которыми пользовался в своих статьях профессор Том, поскольку в данной книге необходимо было избежать употребления одних и тех же символов для обозначения разных величин.

Нахождение «наилучшего» круга для метода экстраполяции, использовавшегося в Мерривейле

Искомый круг должен проходить через точку L, и линия OM должна быть касательной к нему (рис. 7.14). Поскольку

OL = G и OM = 2G, LM = √(5G).

Далее, NM/PN = LM/LO (из подобия треугольников) и, следовательно,

NM = PN×LM/LO = (√5G/2)×√5G/G = 5G/2

В более общей форме, если выразить OM в долях r расстояния между двумя кольями, радиус «наилучшего» круга составит

NM = (1 + 16r²) G/2.

В частном случае, когда r = 1/2, NM = 5G/2. Если r = 1, NM = 17G/2, а при r = 3/4 NM = 5G.