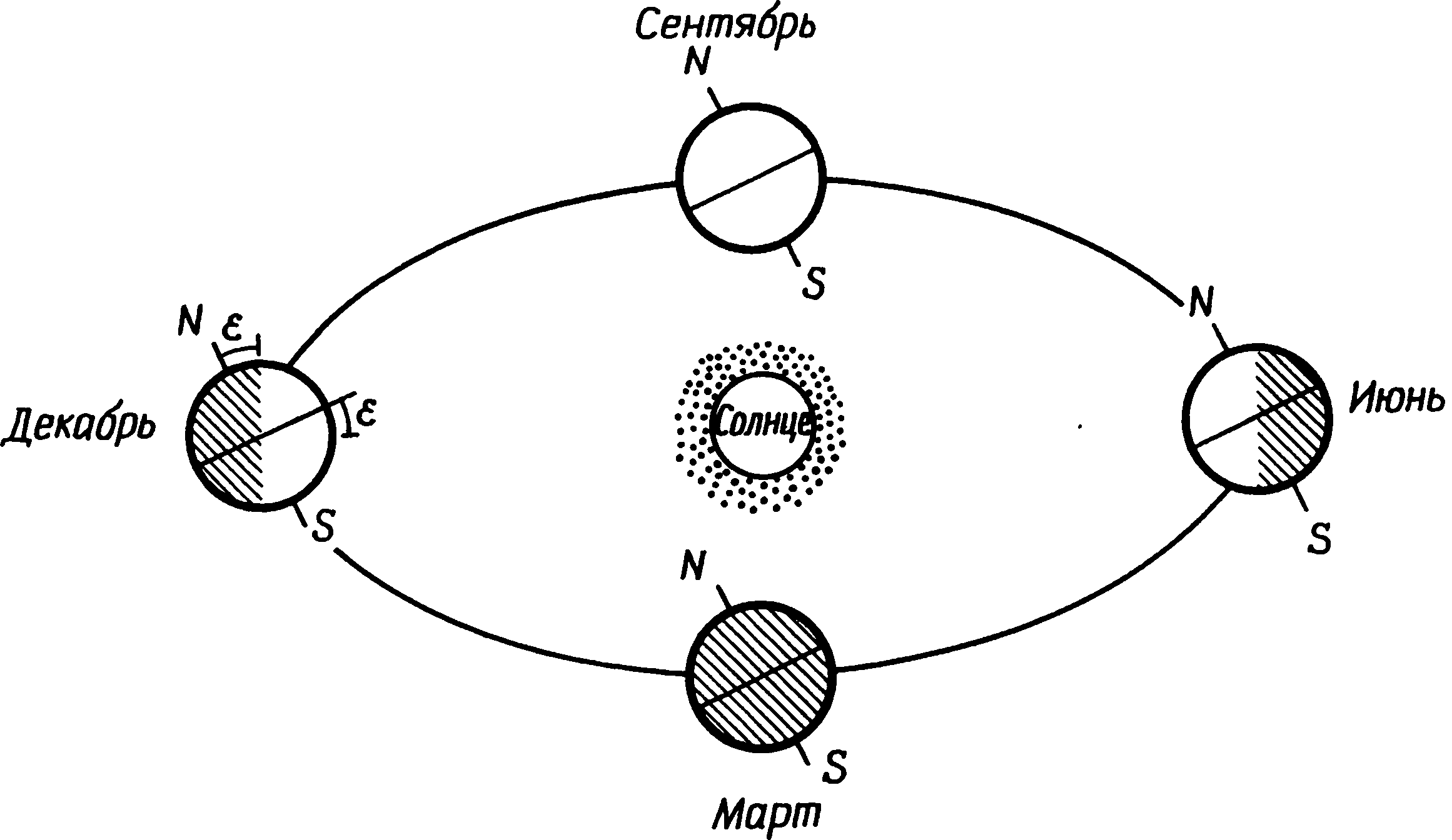
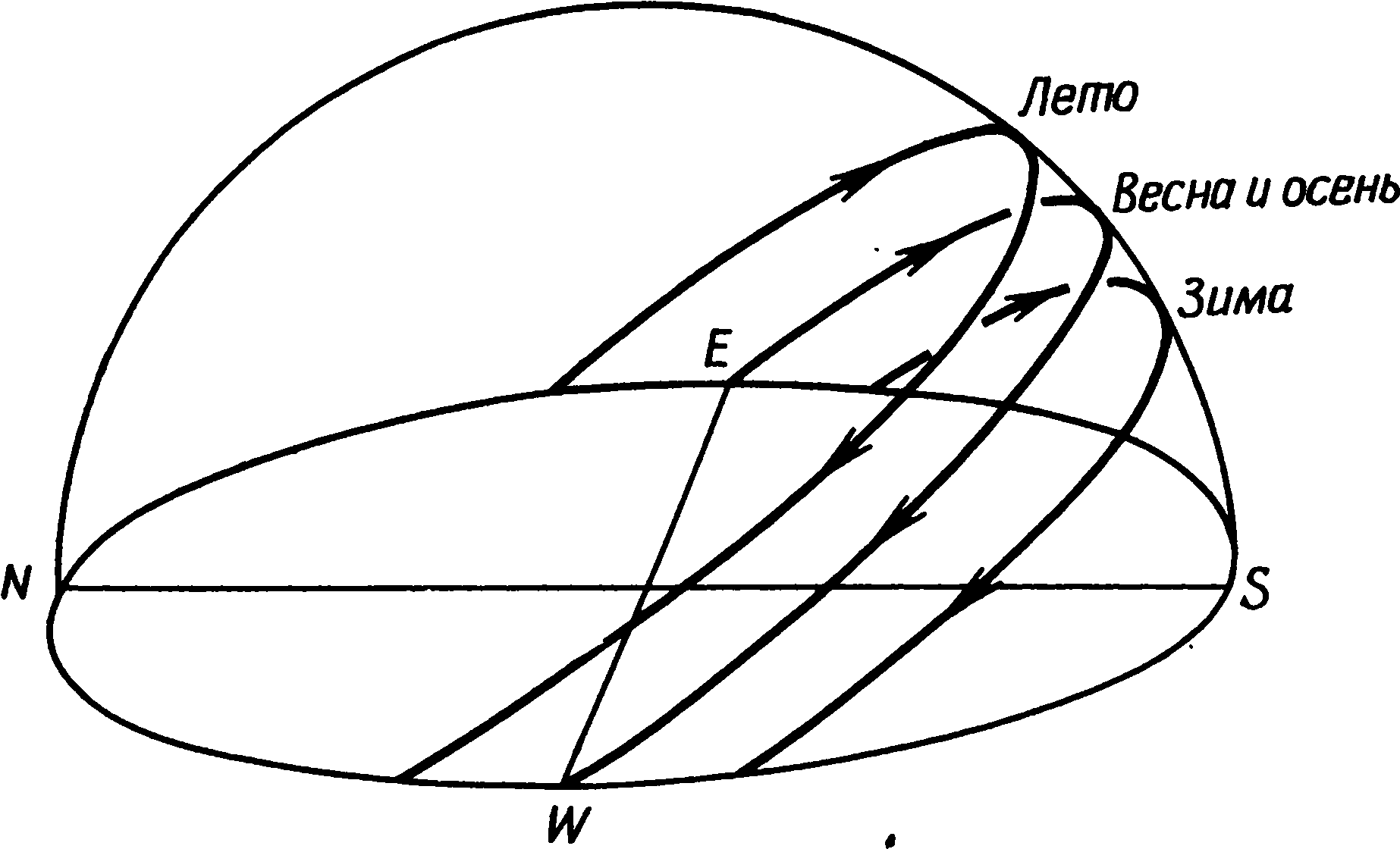
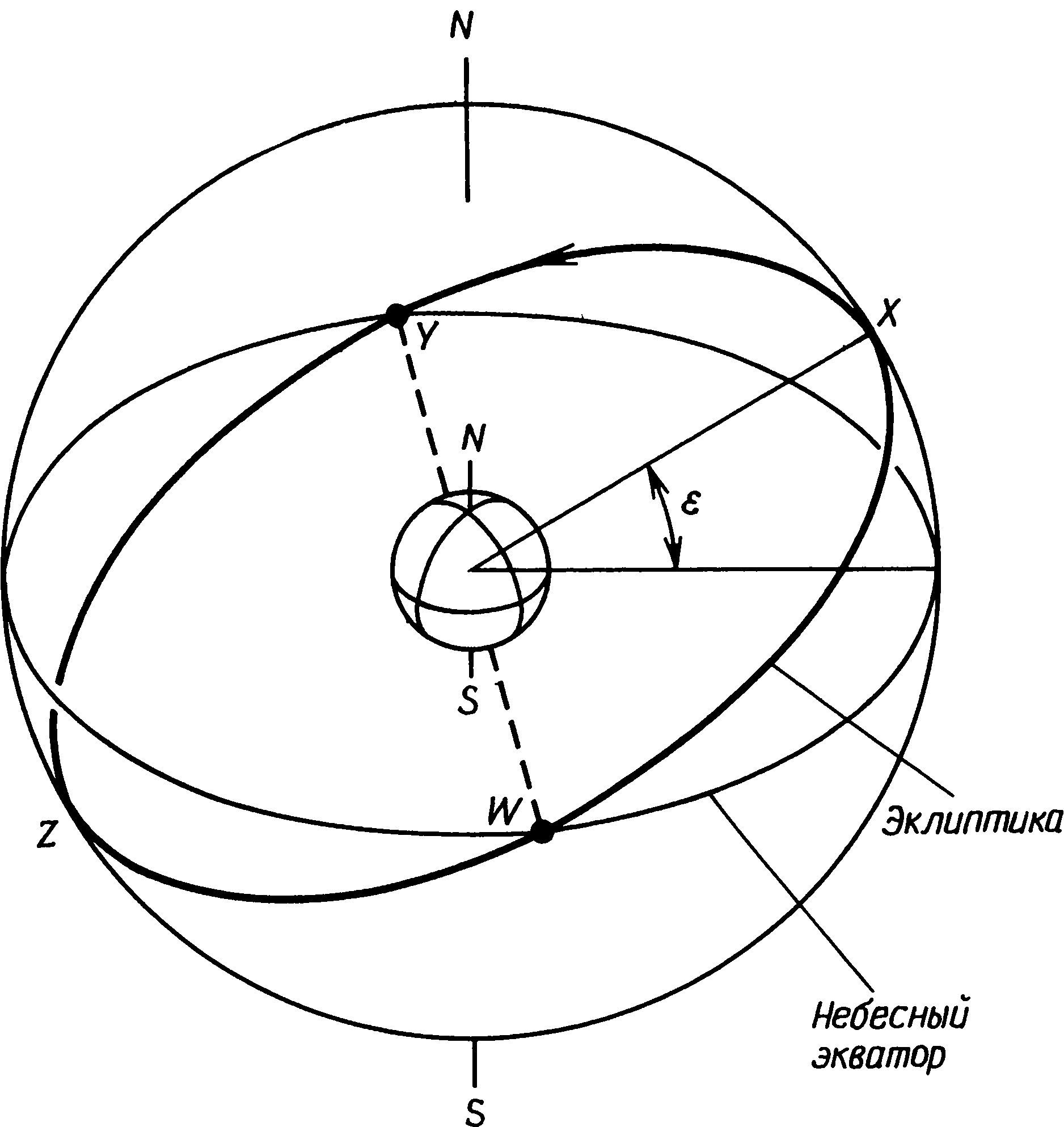
4. Солнце и Луна

Если вы в безоблачную ночь взглянете на небо, то увидите несколько тысяч звезд. Они так далеки от нас, что выглядят светящимися точками, но если бы мы могли к ним приблизиться, то увидели бы, что каждая звезда — это очень большой и очень горячий шар раскаленных газов, испускающий свет и тепло. Наше Солнце — тоже звезда, единственная, которая находится так близко, что мы видим ее как сферическое тело. Солнце отделено от нас расстоянием 150 млн. км, а его диаметр равен 1 392 000 км.

Солнце окружено семьей небесных тел гораздо меньших размеров, которые оно увлекает за собой в своем путешествии через космическое пространство. Их сотни и сотни — главным образом каменных или содержащих металлы глыб, совершенно холодных, если не считать их нагрева за счет солнечного тепла, и невидимых, если только они не сияют отраженным светом Солнца. Самые большие и известные члены Солнечной системы — это девять планет: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун и Плутон. Все планеты обращаются вокруг Солнца в одном направлении по эллиптическим орбитам с очень малым эксцентриситетом.

С Земли движение других планет кажется сложным и прихотливым. Большую часть года они движутся на фоне звезд с запада на восток — ближайшие к нам настолько быстро, что положение их меняется из ночи в ночь. Но по временам, как раз тогда, когда планета выглядит наиболее яркой, кажется, что она останавливается и движется в обратном направлении, а некоторые описывают на небе петлю. Причина в том, что Земля тоже обращается вокруг Солнца, и видимое движение планеты по небу — это результат сложения ее собственного движения с движением Земли.

В древности астрономы Египта, Вавилона и Греции знали самые яркие планеты: Меркурий, Венеру, Марс, Юпитер и Сатурн, — но не могли объяснить их сложные движения и возвели их в ранг богов. Обитатели северо-запада Европы в эпоху неолита и раннего бронзового века также, конечно, должны были обращать внимание на эти планеты, поскольку все они по временам бывают самыми яркими объектами в ночном небе — все, за исключением Меркурия, который всегда находится слишком близко к Солнцу, что затрудняет его наблюдение в северных широтах. Поклонялись они планетам или нет, мы не знаем, и у нас нет возможности установить, пытались ли они систематически следить за их движением, однако можно с достаточной уверенностью предположить, что разобраться в его сложностях им не удалось, а потому, говоря о мегалитической астрономии, планеты следует отбросить.

Земная орбита с эксцентриситетом 0,017 — одна из наиболее приближающихся к круговой планетных орбит. Солнце находится не в центре этого эллипса, но в одном из его фокусов. Вследствие этого расстояние между Землей и Солнцем изменяется от 146 млн. км в январе до 151 млн. км в июле, так что, когда в северном полушарии зима, мы несколько ближе к Солнцу, чем летом. Изменения этого расстояния не являются причиной смены времен года.

Совершая полный оборот вокруг Солнца за один год, Земля, кроме того, вращается вокруг своей оси, как волчок, и один полный ее оборот вокруг оси составляет сутки. На протяжении двадцати четырех часов точка земной поверхности попадает на освещенную Солнцем — дневную — сторону, а затем уходит на темную — ночную — сторону. Земная ось представляет собой воображаемую линию, определяющую положение северного и южного полюсов, и если бы мы посмотрели на Землю из космического пространства со стороны северного полюса, то увидели бы, что она вращается против часовой стрелки. Северная Америка лежит к западу от Европы, и такое вращение перемещает ее на освещенную сторону позже Европы. Чем дальше на запад мы находимся, тем позже приходит к нам каждое время суток (пока не будет достигнута линия перемены даты в Тихом океане). Космонавт на пути к Луне видит, что Солнце не ходит вокруг Земли, и что Земля вращается вокруг своей оси, но мы на ее поверхности вращаемся вместе с ней, и нам Земля представляется неподвижной, а Солнце — ежесуточно обращающимся вокруг нее: нам кажется, что утром оно восходит из-за восточного горизонта, а вечером опускается за горизонт на западе.

Будь земная ось перпендикулярна земной орбите, все было бы очень просто: Солнце восходило бы точно на востоке и заходило бы точно на западе независимо от того, в каком месте на земной поверхности мы находимся. Дни круглый год имели бы одинаковую длину и не было бы смены времен года; происходили бы лишь небольшие колебания температуры из-за того, что расстояние от Земли до Солнца слегка меняется. К счастью, дело обстоит иначе. Ось вращения Земли наклонена к плоскости ее орбиты, или к плоскости эклиптики, под углом около 66,5°. Принято измерять угол наклона не от плоскости орбиты, а от проведенного к ней перпендикуляра, и тогда этот угол составит 23,5°. Поскольку экваториальная плоскость Земли перпендикулярна ее оси, эта величина представляет собой также угол между плоскостью земной орбиты и плоскостью экватора. Для ее наименования имеется общепринятый астрономический термин — наклонение экватора к эклиптике, и у него есть специальный символ: греческая буква эпсилон, ε (рис. 4.1).

Рис. 4.1. Смена времен года на Земле (масштаб не выдержан)

Именно благодаря наклону земной оси на Земле происходит смена времен года. В июне северный полюс Земли наклонен к Солнцу так, что, несмотря на ее вращение, он и прилегающая к нему область не уходят на темную сторону, а постоянно остаются на освещенной, и там царит долгий полярный день. Южный же полюс, наоборот, отклонен от Солнца и погружен в полярную ночь. В северном полушарии Солнце в полдень достигает наибольшей высоты над горизонтом в июне, в южном же полушарии оно в это время ниже всего. Чем выше Солнце на небе, тем сильнее оно греет, и потому в июне в северном полушарии стоит лето, совпадающее по времени с южной зимой.

При обращении Земли вокруг Солнца направление ее оси остается практически неизменным, а потому, когда проходит шесть месяцев и наступает декабрь, ситуация оказывается противоположной. Теперь к Солнцу повернут южный полюс, а северный отклонен от него. Иначе говоря, в южном полушарии лето, а в северном — зима.

На полпути по орбите, между июнем и декабрем, в сентябре и марте, земная ось не наклонена ни к Солнцу, ни от него. Угол, образуемый ею с плоскостью орбиты, по-прежнему составляет 66,5°, но наклонена она под прямым углом к линии, соединяющей Землю с Солнцем. На время возникает та простая ситуация, когда Солнце повсюду на Земле восходит точно на востоке и заходит точно на западе, а день и ночь повсюду равны двенадцати часам. Такие сутки — их в году двое — называются равноденствиями, и они приходятся на 21 марта и 22 сентября с отклонениями от этих дат менее одних суток.

Житель умеренных широт северного полушария, наблюдающий движение Солнца каждый день в течение года, может увидеть следующее (рис. 4.2). Начиная с 20 марта оно каждое утро встает чуть дальше к северу от точного востока и заходит чуть дальше к северу от точного запада. Восходя севернее, Солнце в полдень оказывается в небе выше и день длится дольше. По мере приближения к дню летнего солнцестояния точка восхода смещается к северу все медленнее и 21 июня достигает своего северного предела. В течение нескольких дней почти невозможно заметить какую-либо перемену как в положении на горизонте точек восхода и захода, так и в высоте Солнца в полдень. На протяжении недели, на середину которой приходится самый длинный день года, все дни имеют примерно одну и ту же продолжительность. Солнце словно бы застывает на месте перед тем, как начать свое движение назад, когда оно с каждым днем спускается все ниже.

После дня летнего солнцестояния точки восхода и захода Солнца начинают смещаться к югу, во время осеннего равноденствия оказываются точно на востоке и на западе и достигают своего южного предела 21 декабря. Полуденная высота Солнца по мере наступления зимы уменьшается, и день постепенно становится короче. И вновь, по мере того как точки восхода и захода приближаются к самому южному своему положению, их ежедневное смещение постепенно становится таким малым, что его почти невозможно заметить, и короткие дни непосредственно перед зимним солнцестоянием и после него все имеют примерно одинаковую долготу. В эти дни Солнце словно бы застывает в небе. Летним и зимним солнцестояниями называют те моменты, когда изменение полуденных высот Солнца прекращается.

До сих пор все описание было только приблизительным. Если мы хотим составить календарь, опирающийся на движение Солнца, нам необходимо найти способ точно указывать положения, которые оно занимает в ходе годичного цикла. Например, можно следовать методу, придуманному в неолитическом периоде, т.е. отмечать на горизонте точки восхода и захода в разные времена года. При условии, что на далеком горизонте имеется четкий ориентир, это можно сделать с достаточной точностью, не прибегая к точным математическим расчетам. Точки захода можно определить с помощью постоянных наблюдений, установив в случае необходимости ориентиры, чтобы другие люди тоже знали, куда надо смотреть. Если, с другой стороны, мы хотим проверить направления, отмеченные в прошлом, то практически совершенно невозможно обследовать все памятники и в течение года заново проводить необходимые наблюдения. Для проверки этих направлений мы вынуждены прибегать к математическим методам, что подразумевает использование точных способов определения и измерения направлений.

Рис. 4.2. Движение Солнца по небесной сфере

Можно очень просто определить направление на небесное тело, указав его азимут и высоту. Азимут — это горизонтальный угол, измеряемый по часовой стрелке от истинного севера. Так, азимут точки востока равен 90°, точки юга — 180°, а точки северо-запада — 315°. Высота — это вертикальный угол, измеренный от плоскости горизонта: он положителен, если точка, которую мы указываем, находится над горизонтом, и отрицателен, если она лежит ниже горизонта. Для указания направления на горную вершину азимут и высота очень удобны, поскольку они для нее — постоянные величины. Однако для небесных тел они уже менее удобны, так как все время меняются.

Чтобы указать положение на небе Солнца, Луны и звезд, можно использовать и другую пару углов. Представим себе, что небо — это огромный купол, вроде купола планетария. Приняв небо за сферу, мы можем начертить на нем сетку, сходную с сеткой долгот и широт на земной поверхности. И эти линии будут точным подобием земных долгот и широт в том случае, если мы продолжим плоскость земного экватора, пока она не пересечет воображаемую сферу, дав таким образом линию небесного экватора, от которого мы будем вести отсчет. Линию, проходящую через северный и южный полюсы, мы можем продолжить, пока ее концы не достигнут воображаемой небесной сферы, отметив тем самым северный и южный полюсы мира (рис. 4.3).

Рис. 4.3. Небесная сфера

Эквивалент земной широты на небесной сфере, т.е. угол, измеряемый от небесного экватора, называется склонением. Угол, соответствующий земной долготе, называется прямым восхождением. Для измерения прямого восхождения необходимо принять некоторую нулевую линию отсчета, как во всем мире принята за нулевой меридиан линия, проходящая через Гринвичскую обсерваторию. За линию отсчета прямого восхождения принято считать линию, проходящую через оба небесных полюса и через точку, в которой находится Солнце в момент весеннего равноденствия.

Зрительно представить себе небесную сферу будет легче, если мы взглянем на нее как бы снаружи, а не изнутри, как показано на рис. 4.3. Кроме того, на нем показан путь Солнца по небесной сфере в течение года. В момент весеннего равноденствия Солнце находится в точке W, там, где оно, двигаясь из южной части небесной сферы в северную, пересекает небесный экватор. Именно тогда его склонение из отрицательного становится положительным. С марта по июнь склонение Солнца постепенно увеличивается до максимального значения +23,5°, и в момент летнего солнцестояния оно находится в точке X. Путь, проходимый Солнцем по небесной сфере за оставшуюся часть года, — это дуга XYZ. На этой схеме WXYZ — плоскость земной орбиты, и она образует с плоскостью небесного экватора угол ε.

Процесс проверки направлений начинается с вычисления видимых точек восхода и захода Солнца при разных принимаемых значениях его склонения. Для этого нам необходимо знать географическую широту археологического памятника и высоту Солнца над истинным, или математическим, горизонтом в момент, когда оно появляется над видимым горизонтом. Все эти величины связаны тригонометрическим уравнением, в котором латинские буквы A и h обозначают азимут и высоту Солнца над истинным горизонтом в момент восхода или захода. Греческая буква Φ (фи) обозначает широту места, а δ (дельта) — склонение Солнца. Тогда

cos A = (sin Φ − sin Φ sin h) / (cos Φ cos h) (1)

Смысл тригонометрических функций объясняется в приложении В.

Из трех неизвестных величин — Φ, δ и h — легче всего найти широту Φ, так как она приводится на всех крупномасштабных картах Государственного картографического управления. Однако чтобы получить нужные результаты, необходимо потрудиться и найти широту памятника с точностью до 0,01°. Координатная сетка на картах Британских островов не ориентирована точно на север, а потому градуировка широт на боковых сторонах карты не совпадает с линиями координатной сетки. Широту всегда следует вычислять по положению ближайших меток, которые разделены интервалами, равными 5′.

Склонение Солнца (или Луны) для любого дня года можно найти в астрономическом ежегоднике. Вероятнее всего, археолога в основном будет интересовать склонение Солнца в дни солнцестояний. В настоящее время оно составляет примерно 23,5°, но оно не всегда было таким. Сложные гравитационные взаимодействия между Землей и другими планетами приводили к тому, что наклон эклиптики на протяжении столетий медленно менялся и к нашему времени уменьшился, а в 4000 г. до н.э. он составлял примерно 24,1°. Разница невелика, однако ее необходимо учитывать. Точное значение для любой даты между 4000 и 1000 г. до н. э. может быть взято из табл. 4.1 и проинтерполировано для промежуточных дат.

Таблица 4.1. Наклон эклиптики ε с 4000 по 1000 г. до н. э.

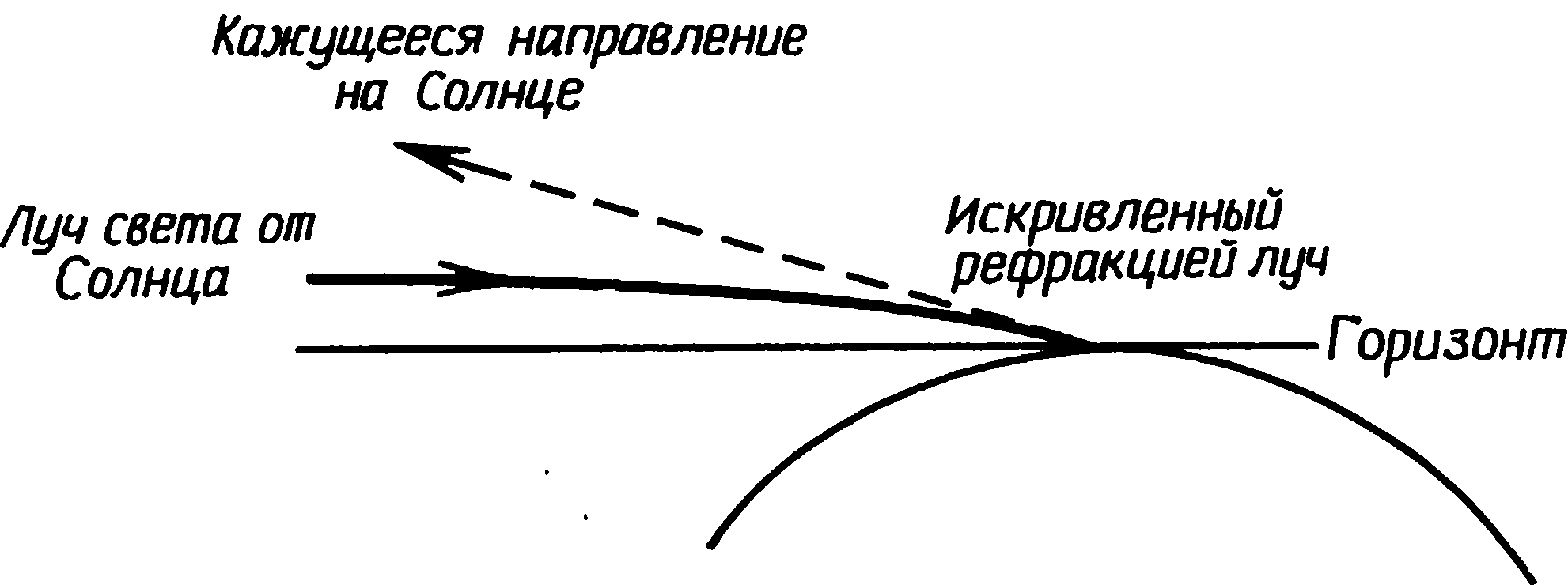
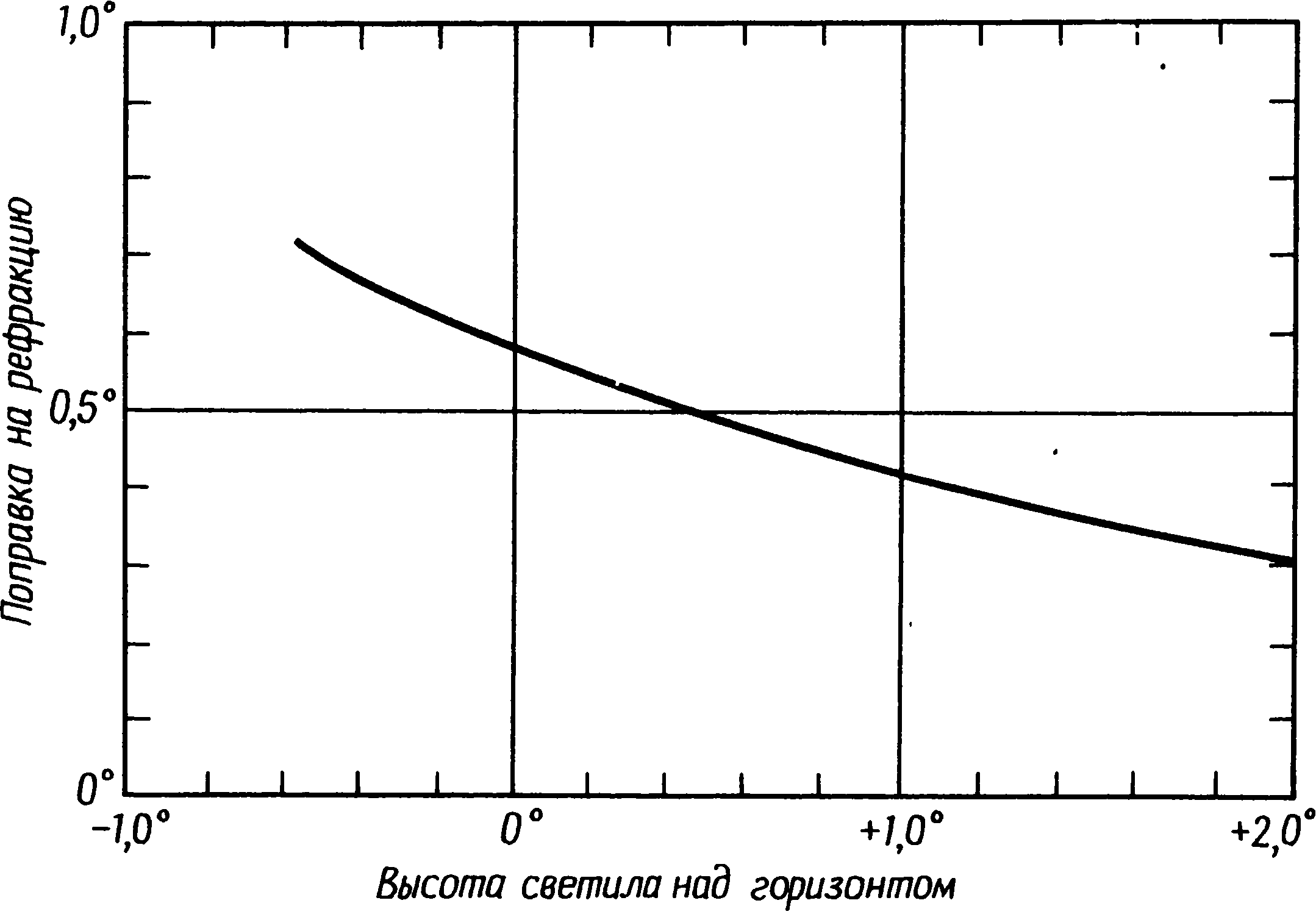
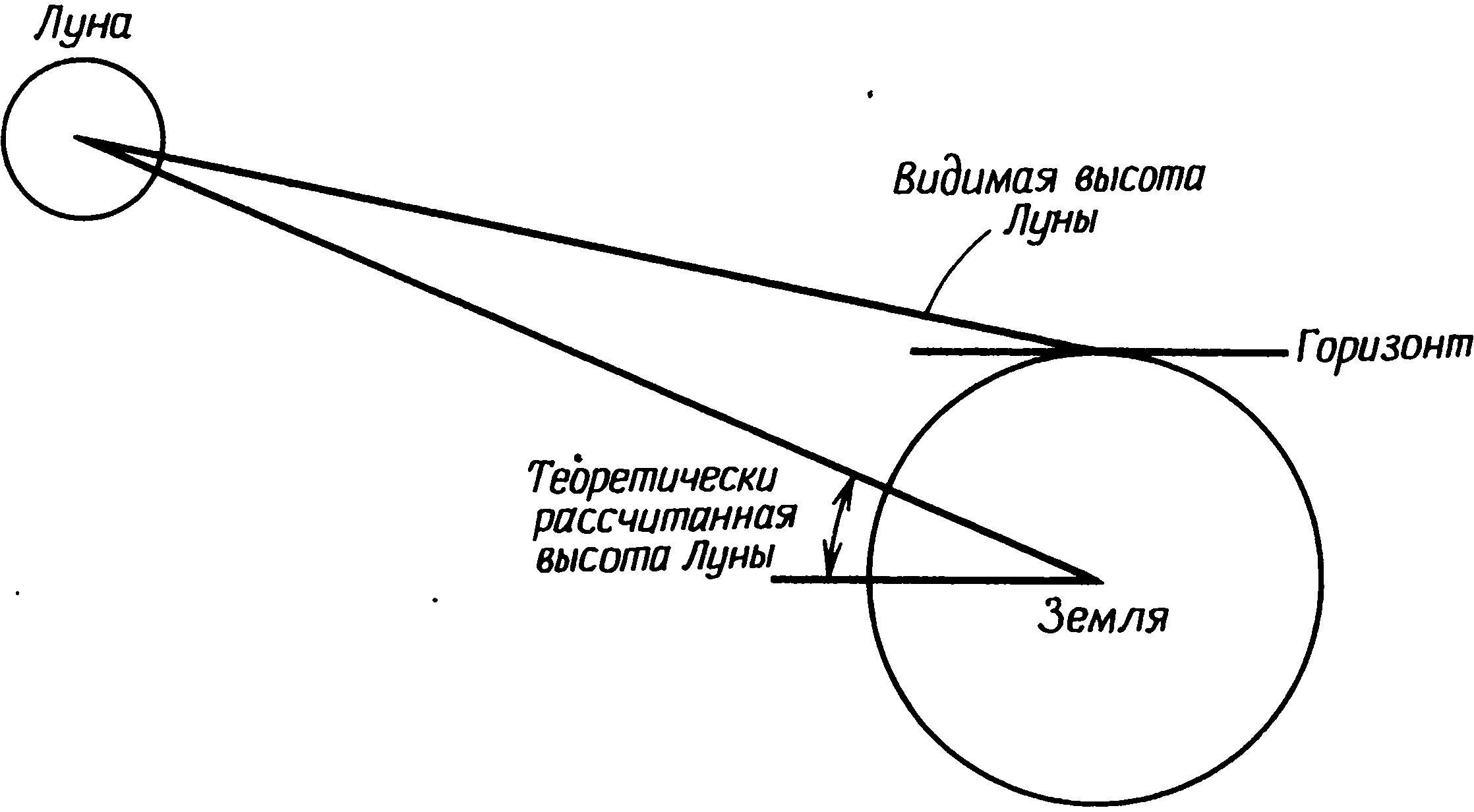
Именно это небольшое изменение наклона эклиптики Норман Локь-ер и пытался использовать в своем методе датировки Стоунхенджа. Мы можем определить азимут точки восхода Солнца в день летнего солнцестояния упрощенным методом и заодно показать, каким образом вычисляется этот азимут. Для простоты примем, что видимый горизонт совпадает с истинным; тогда в уравнении (1) угол h = 0°, поскольку sin 0° = 0, а cos 0° = 1, уравнение (1) упрощается:

cos A = sin δ/cos φ. (2)

Широта Стоунхенджа равна 51,178° и, следовательно, cos φ = 0,6269. Мы можем найти азимут точки восхода Солнца в день летнего солнцестояния в 2000 г. до н. э., взяв из табл. 4.1 для солнечного склонения значение 23,93°, откуда sin δ = 0,4056, а cos A = 0,4065:0,6269 = 0,6470. Это дает A = 49,68°. Повторив те же расчеты для 1500 г. до н. э., получаем A = 49,79°. Величина A изменилась за 500 лет всего на 0,1°, что дает 0,02° за столетие. Когда Локьер попытался установить дату постройки Стоунхенджа, измерив азимут оси Аллеи, а затем сравнив его с рассчитанными азимутами, теоретически он был вполне прав, но, как объяснялось в гл. 1, результат оказался недостаточно точен. Профессор Том в последние годы применяет тот же метод для датировки других археологических памятников. Он выбирает направления, отмеченные очень точными ориентирами, обычно выемкой на далеком горизонте.

Вычисляя два значения азимута, мы хотели только показать скорость их изменения, а не вывести истинные числа для указанных дат. Приняв h равным нулю, мы получим неточные ответы, хотя разница между двумя азимутами не содержит значимой ошибки. При проверке конкретной линии визирования приближение h = 0° дает неверные результаты и не должно использоваться (за исключением предварительной прикидки, когда проверяется, действительно ли предполагаемый ориентир находится в приблизительно верном направлении).

Высоту видимого горизонта можно измерить непосредственно на месте с помощью теодолита (наилучший способ) или рассчитать по профилю местности, снятому с крупномасштабной карты. Это надо делать внимательно, потому что очень легко ошибиться и начертить профиль холмов, не заметив, что видимый горизонт полностью или частично обрисован линией более удаленной гряды. Выбрав профиль, надо рассчитать по нему угловую высоту горизонта, а для этого полезно знать, что подъем в 1 м на расстоянии 1 км соответствует вертикальному углу 0,057°. Когда видимый горизонт очень удален, приходится учитывать и кривизну земной поверхности, для чего из угловой высоты горизонта следует вычитать 0,0045° на каждый километр расстояния от места наблюдения.

Высота видимого горизонта, однако, еще не дает значения h, которое можно было бы подставить в уравнение (1). Есть два других фактора, которые также надо учитывать, — рефракция и параллакс.

Рис. 4.4. Рефракция света в атмосфере

Рефракция — это искривление световых лучей атмосферой. Эффект атмосферной рефракции часто можно наблюдать в жаркий летний день, когда едешь на машине по широкому шоссе. Впереди словно бы появляются темные «лужи», и если по ту сторону такой «лужи» оказывается встречная машина, иногда видно ее отражение, словно в «луже» настоящая вода. На самом же деле это миражи, которые исчезают при вашем приближении. Их можно объяснить искривлением светового луча, который, проходя через теплый, а потому менее плотный воздух в нескольких сантиметрах от нагретой поверхности шоссе, преломляется вверх.

Точно так же атмосфера искривляет лучи, идущие от Солнца. Когда Солнце оказывается вблизи горизонта, кажется, будто оно находится на той же высоте, что и дальние холмы, однако на самом деле это не так. Лучи, войдя в более плотные слои атмосферы около поверхности Земли, искривились вниз, и в результате Солнце в небе немножко «приподнялось» (рис. 4.4). Благодаря рефракции восход наступает чуть раньше, а заход — чуть позже, чем это было бы, не будь у Земли атмосферы. Рефракцию можно учесть в уравнении (1), вычитая из h небольшую поправочную величину. Величина эта зависит от высоты горизонта. Если высота видимого горизонта равна нулю, поправка составит 0,55°, но для более высокого горизонта она меньше. Значение поправки можно получить из графика на рис. 4.5, на котором показаны поправки на рефракцию для разных угловых высот видимого горизонта.

Название второго фактора — параллакс — представляет собой астрономический термин для обозначения очень простого явления. Если вы будете держать перед собой на расстоянии вытянутой руки карандаш и по очереди прищуривать то один, то другой глаз, вам покажется, что карандаш прыгает на фоне стены из стороны в сторону. Это и есть параллакс — видимое положение предмета зависит от того, где вы находитесь, когда смотрите на него. А все значения склонения Солнца и Луны, которые мы берем из астрономических ежегодников, рассчитаны для наблюдателя, находящегося в центре Земли. Такой подход может показаться странным, но зато этими значениями можно пользоваться в любом месте Земли. Как видно на рис. 4.6, когда Солнце и Луна находятся на небосводе низко, их положение для наблюдателя на поверхности Земли несколько отличается от приведенного в ежегодниках. Как и в случае с рефракцией, параллакс можно учесть, введя небольшую поправку, равную 0,002° для Солнца (величина настолько малая, что ею можно пренебречь) и 0,95° для Луны (величина заметная). Из-за параллакса Луна восходит позже и заходит раньше, чем предсказывают ежегодники, а потому действие его обратно действию рефракции. Поэтому указанная поправка прибавляется к h.

Рис. 4.5. Изменение рефракции в зависимости от высоты светила над горизонтом

В совокупности все эти факторы дают следующее правило: h = (высота горизонта) − (поправка на кривизну земной поверхности) + (параллакс) − (рефракция).

Подставив в уравнение (1) значение, полученное нами для h, мы найдем азимут той точки горизонта, где будет видна ровно половина солнечного диска. К сожалению, нам не известно, какой именно момент астрономы неолита и раннего бронзового века принимали за момент захода: первое касание диском Солнца линии горизонта, когда горизонт делит его пополам или последний его проблеск перед полным исчезновением. Возможно даже, что в разные эпохи они избирали разные моменты. Если они считали наиболее важным точно зафиксировать направление на место захода Солнца, то легче всего для наблюдения был бы последний проблеск. На ровном горизонте его можно локализовать очень точно. С другой стороны, довольно трудно решить, когда диск Солнца делится горизонтом точно пополам, и так же нелегко установить, когда заходящий солнечный диск коснулся горизонта — главным образом из-за его ослепительной яркости и из-за эффекта дрожания, который вызывается неравномерным преломлением лучей в атмосфере. Отметить место появления солнечного диска при восходе труднее, чем место его исчезновения при заходе, если только вы не знаете почти совершенно точно, где именно он появится.

Рис. 4.6. Параллакс

Не составляет ни малейшего труда ввести необходимую поправку в величину h, чтобы найти азимут точки, где исчезает (или появляется) солнечный диск. Для нахождения места исчезновения диска надо вычесть из h угол 0,25°, который равен половине углового диаметра солнечного диска. Для момента первого касания диском горизонта прибавьте 0,25°. Поскольку видимые диаметры Солнца и Луны по счастливой случайности почти одинаковы, эти поправки применимы для них обоих.

Когда горизонт горист или холмист, он представляет современному исследователю больше возможностей для того, чтобы наметить путь восходящего или заходящего Солнца либо восходящей или заходящей Луны. Лучший способ — сначала вычертить на миллиметровке профиль горизонта, а затем найти азимуты центра диска для нескольких высот как над, так и под горизонтом. При этом надо учесть влияние рефракции, а для Луны — и параллакса. Рисунки вроде рис. 6.4 можно получить, просто вычерчивая круги в соответствующем масштабе и соединяя их окружности касательными. Если видимый горизонт низок, путь заходящего светила будет слегка искривлен из-за того, что для разных высот рефракция будет различна. Хотя это довольно скучная работа, обычно имеет смысл делать такой набросок, так как он показывает солнечный или лунный заход таким, как он на самом деле выглядел в мегалитические времена, и дает правильное представление о пути заходящего светила по отношению к неровностям горизонта.

Вот рабочий пример. Представим себе, что мы хотим узнать точки восхода и захода Солнца в дни летнего и зимнего солнцестояний — всего четыре направления — для памятника, расположенного на той же широте, что и Стоунхендж, с ровным, не очень отдаленным горизонтом, имеющим видимую высоту около 1,0°. Примем за момент восхода и захода то мгновение, когда виден только верхний краешек солнечного диска. Тогда широта φ равна 51,178° и, следовательно, sin φ = 0,7791, а cos φ = 0,6269 (взято из таблиц тригонометрических функций). В этом примере мы можем пренебречь кривизной земной поверхности, поскольку горизонт не слишком удален, и параллаксом, поскольку параллакс Солнца очень невелик. Отсюда

h = 1,0° (высота видимого горизонта) − 0,4° (рефракция, см. рис. 4.5) − 0,25° (половина диска) = +0,35°,

Следовательно, sin h = 0,0061, а cos h = 0,9998.

Остальные расчеты удобнее свести в таблицу (табл. 4.2).

Из табл. 4.2 видно, что cos A одинаков и для восхода, и для захода Солнца в день зимнего солнцестояния, однако азимуты их различны. Это объясняется тем, что косинус любого угла равен также косинусу 360° минус тот же угол, т.е. cos A = cos (360° − A). Поэтому расчеты, несмотря на одно и то же значение косинуса, дают два результата, и азимут точки захода Солнца в день зимнего солнцестояния получается путем вычитания азимута на точку солнечного восхода из 360°. То же самое относится к восходом и заходам в день летнего солнцестояния.

Таблица 4.2. Расчет азимутов точек восхода и захода Солнца

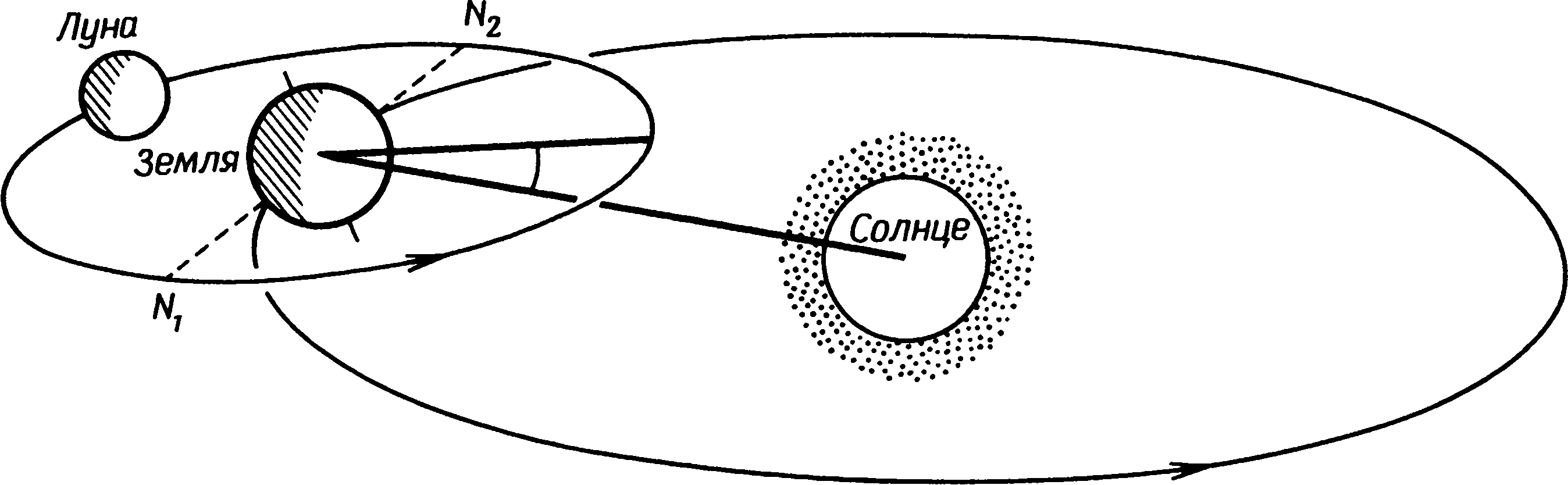
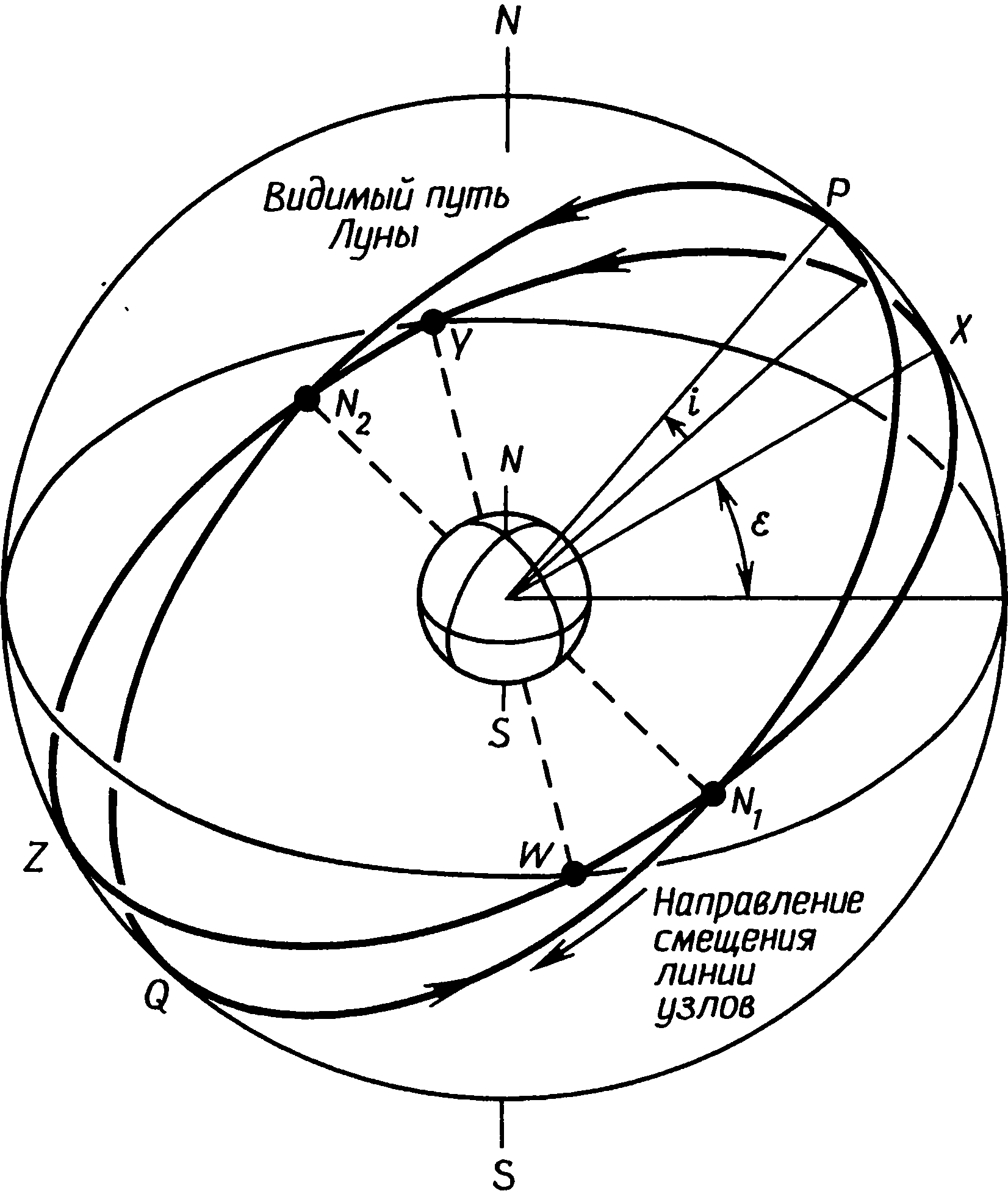
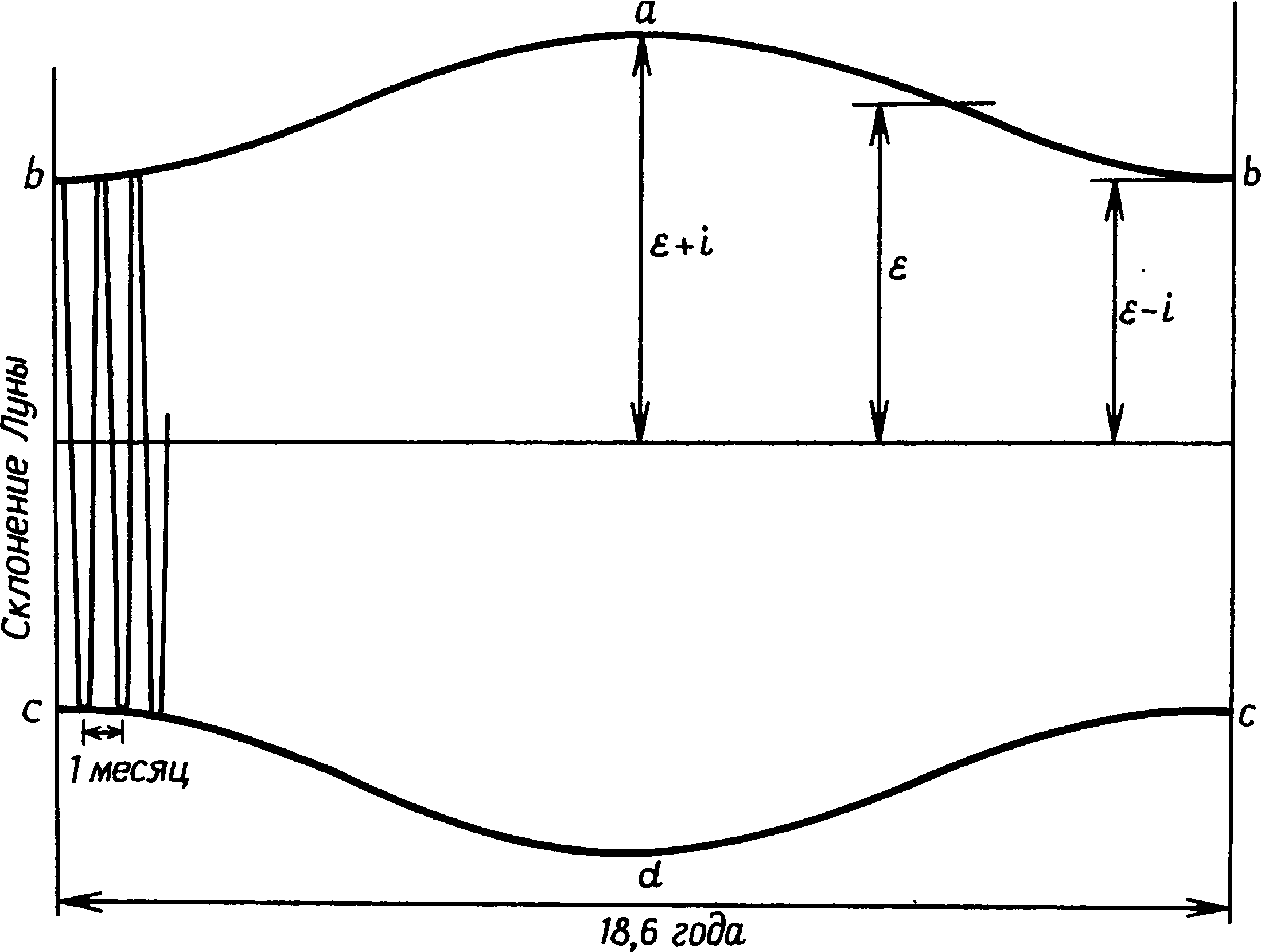
Если нанести эти четыре направления на карту, они будут выглядеть, как на рис. 1.2. Точки восхода Солнца в день летнего солнцестояния и захода в день зимнего солнцестояния не совершенно точно противоположны, а из-за влияния рефракции они не были бы противоположны, даже если бы высота всего видимого горизонта была равна нулю.

Если наблюдаемое с Земли движение Солнца довольно просто, то движение Луны чрезвычайно сложно. Луна обращается вокруг Земли в том же направлении, в каком Земля обращается вокруг Солнца. Ее орбита наглядно показана на рис. 4.7, где масштабы изображения орбит и небесных тел сильнейшим образом искажены. Диаметр орбиты Луны составляет 1/360 диаметра земной орбиты, и, изображенная в том же масштабе, она практически превратилась бы в точку. Период обращения Луны составляет примерно 27⅓ суток, а среднее расстояние между ней и Землей около 384000 км. Плоскость ее орбиты не совпадает ни с плоскостью небесного экватора, ни с плоскостью земной орбиты, а расположена под углом 5,14° к этой последней. Луна пересекает плоскость эклиптики дважды в месяц, и две точки пересечения орбит (так называемые узлы) помечены на рис. 4.7 буквами N₁ и N₂.

Рис. 4.7. Орбита Луны в пространстве (масштаб не выдержан)

Нас, собственно говоря, интересуют не реальные расстояния до Солнца и Луны, а их видимое положение на небосводе. И гораздо удобнее оставить попытки изобразить фактические движения Луны в пространстве и вернуться к их изображению на небесной сфере, как это показано на рис. 4.8. На нем видимый путь Луны по небу изображен кругом N₁PN₂Q, а точки N₁ и N₂ показывают узлы лунной орбиты. Узел N₁ называется восходящим узлом, потому что, когда Луна пересекает эклиптику в этой точке, она движется к северу. Узел N₂ — нисходящий. Угол между плоскостью лунной орбиты и плоскостью эклиптики, равный 5,14°, обозначается буквой i. Этот угол не изменился по сравнению с доисторическими временами и в отличие от ε не требует поправки для конкретной даты.

На протяжении месяца Луна совершает полный оборот N₁PN₂QN₁. Наибольшего положительного склонения она достигает в точке P, а наибольшего отрицательного — в точке Q. За 27⅓ суток склонение Луны проходит весь цикл от наибольшего до наименьшего. Ее движения следуют той же схеме, что и движения Солнца, но только происходят в тринадцать раз быстрее.

Рис. 4.8. Движение Луны по небесной сфере

Однако тут имеется одно очень важное осложнение — плоскость лунной орбиты тоже вращается. Линия узлов совершает полный оборот каждые 18,6 года. Посмотрите на рис. 4.9 и сравните его с рис. 4.7. Они практически одинаковы, только лунная орбита наклонена в противоположную сторону, точно так, как это и должно быть через 9,3 года. На рис. 4.7 плоскость лунной орбиты гораздо ближе к плоскости земного экватора, чем на рис. 4.9.

Движение узлов лунной орбиты проиллюстрировано на рис. 4.8; орбита показана незадолго до того, как она достигла максимального наклона к небесному экватору. При максимальном наклоне углы ε и i суммируются, а поэтому угол наклона лунной орбиты к небесному экватору равен ε + i т. е. достигает примерно 29°. Когда линия узлов сделает пол-оборота, точка P окажется над точкой Z, а точка Q будет находиться между точкой X и эклиптикой. Угол i будет вычитаться из угла ε, и наклон лунной орбиты к небесному экватору будет равен ε − i, т. е. примерно 19°.

Рис. 4.9. Орбита Луны в пространстве через девять лет после изображенной на рис. 4.7 (масштаб не выдержан)

Мы уже говорили о том, что склонение Луны каждый месяц изменяется от максимального до минимального и обратно. Теперь мы видим, что амплитуда этого изменения в определенные периоды достигает наибольшего значения от примерно 29° севернее небесного экватора до примерно 29° южнее его. Мы можем сказать, что склонение Луны изменяется от +(ε + i) до −(ε + i). Когда Луна оказывается в крайнем положении, ее называют «высокой», потому что она на протяжении примерно трех лет ежемесячно достигает в небе почти одного и того же максимума высоты. В это время ее движения наиболее эффектны: она не только ежемесячно поднимается в небе на самую большую высоту, но две недели спустя видна очень низко и в северных областях Шетландских островов едва восходит над горизонтом. Эти движения, несомненно, были очень заметны для доисторических людей.

Через девять с небольшим лет после этого лунная орбита завершает свой полуоборот, и ежемесячные колебания склонения становятся гораздо меньше — от примерно 19° севернее небесного экватора до примерно 19° южнее его, т. е. от +(ε − i) до −(ε − i). В это время Луну называют «низкой». С точки зрения наблюдателя движения «низкой» Луны гораздо менее эффектны, чем движения «высокой». Ее максимальная высота в небе примерно на 10° меньше, а минимальная высота на 10° больше, так что изменения ее высоты за месяц далеко не так велики.

Эти колебания можно изобразить на диаграмме вроде рис. 4.10, показывающего ежемесячные изменения склонения Луны, на которые влияет вращение лунной орбиты с периодом 18,6 года. Собственно говоря, эта схема несколько условна, потому что в периоде длиной 18,6 года на самом деле должно было бы уложиться 242 месячных цикла. При попытке начертить их с большей точностью они оказались бы настолько тесно расположенными, что просто слились бы.

Рис. 4.10. Ход изменения склонения Луны за период 18,6 года

На рис. 4.10 показано, что склонение «низкой» Луны изменяется между b и c, а склонение «высокой» — между a и d. В последний раз «высокая» Луна наблюдалась в апреле 1969 г. и снова будет наблюдаться в конце 1987 г. «Низкой» она была в августе 1977 г.

Так же как с помощью уравнения (1) мы могли рассчитать точки восхода и захода Солнца, мы можем найти точки восхода и захода Луны. Метод точно такой же, однако нельзя забывать о поправке на параллакс. Имеются четыре крайних положения для «высокой» Луны и еще четыре для «низкой» Луны. На рис. 1.3 показано, как эти восемь направлений распределяются по горизонту для места, находящегося на широте Стоунхенджа.

Люди, пишущие о мегалитической астрономии, при указании точек восхода Солнца и Луны, часто используют своего рода стенографию. Они говорят, например, о лунном восходе (ε + i), определяя его по склонению Луны в момент восхода. Это удобнее (и короче), чем описания, использованные Хокинсом, вроде «самая северная точка восхода зимней полной Луны». Профессор Том расширяет эту систему обозначений, введя в нее и диаметр Луны. Согласно его системе, половина диаметра лунного диска обозначается через s, так что, когда он на одной из своих схем помечает направление буквами (ε + i + s), это подразумевает направление на точку, где верхний край лунного диска появляется над горизонтом.

В гл. 1 я упомянул, что, по мнению профессора Хокинса, Стоунхендж мог использоваться как вычислительная машина для предсказания лунных затмений. Чтобы понять эту и сходные с ней гипотезы, необходимо кое-что знать о механизме затмений. Лунное затмение происходит потому, что Луна попадает в тень Земли и становится для нас почти невидимой. Чтобы это произошло, Солнце, Луна и Земля должны находиться на одной прямой и Луна должна оказаться в противоположной от Солнца части неба, иначе говоря, должно быть полнолуние. Солнечное затмение случается, когда Луна проходит между Солнцем и Землей, отбрасывая тень на земную поверхность. Опять-таки Солнце, Луна и Земля должны оказаться на одной прямой, но на этот раз Солнце и Луна должны быть по одну сторону от Земли. Солнечное затмение может произойти только в новолуние.

Если бы плоскость орбиты Луны не была наклонена по отношению к плоскости земной орбиты на угол 5,14°, лунные и солнечные затмения происходили бы ежемесячно. Но из-за этого наклона они происходят только тогда, когда Луна в новолуние или полнолуние находится вблизи одного из узлов своей орбиты. Поскольку диаметры и Земли, и Луны исчисляются тысячами километров, Луна не обязательно должна оказаться точно в узле. Диаметр наиболее темной части земной тени на расстоянии лунной орбиты примерно вдвое превышает диаметр Луны, и затмение может произойти, когда Луна находится в любом месте этой тени. Точно так же солнечное затмение происходит, если лунная тень падает на поверхность Земли в любом месте между северным и южным полюсом. Солнечное или лунное затмение может произойти только при условии, что полнолуние или новолуние наступит не раньше, чем за 17 суток до, или не позже, чем через 17 суток после того момента, когда Луна окажется в одном из узлов своей орбиты. Этот период в 34 дня можно назвать «эпохой затмений».

Между солнечными и лунными затмениями существует очень важное различие. Тень Луны, падающая на Землю, очень невелика и вследствие вращения Земли скользит по ее поверхности. Наблюдать полное солнечное затмение могут только те, кто находится в узкой полосе, по которой скользит лунная тень — самая широкая ее часть не превышает 180 км. За пределами этой полосы наблюдается частное затмение, при котором Луна заслоняет только часть солнечного диска. Частные солнечные затмения, кроме тех случаев, когда закрывается значительная часть диска или когда они происходят на восходе и на закате, заметить трудно, а поскольку люди лишь очень редко смотрят прямо на Солнце, вполне возможно, что обитатели северо-западной Европы во времена неолита или раннего бронзового века даже не знали, что такие затмения случаются. На протяжении этого долгого периода лишь очень немногим людям доводилось видеть полное солнечное затмение. Для тех, кто его видел, это, конечно, было потрясающим событием, но повторялось оно столь редко, что они были совершенно неспособны обнаружить периодичность солнечных затмений. Более мы касаться их не будем, так как для мегалитической астрономии они никакой роли не играли.

Лунные затмения наблюдаются гораздо чаще. Когда случается лунное затмение, оно видно одновременно с половины земной поверхности, а так как длится оно несколько часов, то частично его можно наблюдать (если погода ясная) более чем с половины земной поверхности. В среднем с каждого полушария Земли можно видеть примерно одно лунное затмение ежегодно. Хотя лунные затмения не столь эффектны, как солнечные, они тем не менее достаточно бросаются в глаза и, несомненно, должны были производить глубокое впечатление на доисторических людей любой эпохи. Учитывая относительную частоту этих затмений, мы не можем отбросить возможность того, что в неолите или в раннем бронзовом веке была открыта определенная закономерность в повторении лунных затмений.

Мы уже говорили о том, что лунные затмения происходят только в полнолуния и что Луна должна при этом находиться вблизи одного из узлов своей орбиты. Поскольку узлов два, каждый год возможны два лунных затмения, разделенные шестимесячным периодом. Период обращения узлов равен 18,6 года, что означает ежегодное их смещение примерно на 20°. Солнце движется по эклиптике со скоростью около 1° в сутки (360° за 365,25 суток), так что изменение положения узлов на 20° означает, что направление на Солнце совпадает с узлами каждый год на 20 дней раньше, чем в предыдущем году. (Узлы движутся навстречу годичному движению Солнца.) Это приводит к тому, что лунные затмения каждый год происходят в среднем на 20 дней раньше, чем в предыдущем году.

В этом описании реальное положение вещей сильно упрощено. Продолжительность периода между возвращениями Луны в одну и ту же фазу (этот лунный месяц носит в астрономии название синодического), т.е., например, между двумя новолуниями, составляет 29,53059 суток, а 12 синодических месяцев равны 354,37 суток. Итак, 12 синодических месяцев на 10,63 суток короче, чем год, состоящий из 365 дней. Поэтому на самом деле затмения в течение нескольких лет происходят на 10—11 дней раньше, чем в предыдущем году, и место затмения год за годом все дальше отходит от узла, пока, наконец, день полнолуния не окажется так далеко от дня прохождения Луной узла, что затмение уже произойти не может. Затем в год незаметно включается тринадцатый синодический месяц, и последовательность начинается вновь.

В цикле затмений есть и другие интересные закономерности. В табл. 4.3 перечисляются все лунные затмения с 1913 по 1988 г. Для каждого года приводится дата полнолуния, ближайшего к дню зимнего солнцестояния, а также склонение этой полной Луны. (Собственно говоря, приводится максимальное склонение для данного месяца, но оно обязательно достигается Луной не далее, чем на двое суток позже или раньше полнолуния). Буквы «п», «ч», «в» и «н» в скобках после дат затмений означают «полное», «частное», «видимое» и «невидимое»; они характеризуют затмение и показывают, можно ли было (или будет) увидеть его на северо-западе Европы. За этот период в 76 лет насчитывается 112 затмений; 62 из них (55%) являются полными, а 55 (49%) можно увидеть в Европе. В среднем наблюдается заметно меньше одного затмения в год и одно полное затмение каждые два года.

Стоит рассмотреть связь между датами затмений и склонениями Луны. «Высокая» Луна наблюдалась в 1913, 1932, 1950 и 1969 гг., а «низкая» — в 1922, 1940 и 1959 гг. (Максимальное склонение в большинстве случаев определяет особенности затмений в данном году, хотя следует учитывать, что в таблице приведены максимальные склонения для декабря, а не самое большое его значение для всего года.) В годы «высокой» и «низкой» Луны затмения, если они вообще происходили, приходились на полнолуния, ближайшие к весенним и осенним равноденствиям (21 марта и 22 сентября). В промежуточные периоды затмения происходили вблизи летних и зимних солнцестояний (21 декабря и 21 июня).

Даже эти немногие пока упомянутые факты дают значительный материал для успешного предсказания затмений. Необходимо просто провести достаточное число наблюдений точек восхода и захода Луны, чтобы установить, какой стадии своего цикла длиной в 18,6 года она достигла. Затем при наличии достаточно точного календаря и каких-то возможностей отмечать даты полнолуний можно будет правильно предсказывать большинство затмений или, вернее, «эпох затмений».

В табл. 4.3 скрыты некоторые числовые совпадения, которые могут быть обнаружены только после многих лет наблюдений и регистрации. Если вы будете читать таблицу по горизонтали, то увидите, что через 19 лет затмения часто приходятся на те же самые дни года. Объясняется это тем, что 19 лет почти точно равны 235 синодическим месяцам. Длина года (того, который мы используем в календаре и который астрономы называют тропическим) составляет 365,2422 суток. Длина синодического месяца 29,53059 суток. Следовательно,

19 тропических лет = 6939,60 суток,
235 синодических месяцев = 6939,69 суток.

Таблица 4.3. Лунные затмения с 1913 по 1988 г. Если в дате полной зимней Луны стоит январь, имеется в виду январь следующего года

Таким образом, через 19 лет фазы Луны повторяются в те же самые дни, хотя и не в те же часы. Эта закономерность носит название метонова цикла, так как считается, что ее открыл греческий астроном Метон в 433 г. до н.э. Метонов цикл — это не цикл затмений, и совпадение дат затмений через 19 лет прекращается после двух повторений. Период обращения лунных узлов не совпадает с этим циклом.

Однако существует и истинный цикл затмений, называемый саросом и открытый в глубокой древности халдейскими астрономами. Ранее в этой главе я объяснил, что, поскольку лунные узлы вращаются навстречу Солнцу, ему требуется на 20 дней меньше года, чтобы завершить один полный оборот по отношению к узлам лунной орбиты. Точнее говоря, время, необходимое для того, чтобы Солнце проделало такой полный оборот, составляет 346,62 суток. Этот период называется драконическим годом. Отсюда

19 драконических лет = 6585,78 суток,
223 синодических месяца = 6585,32 суток.

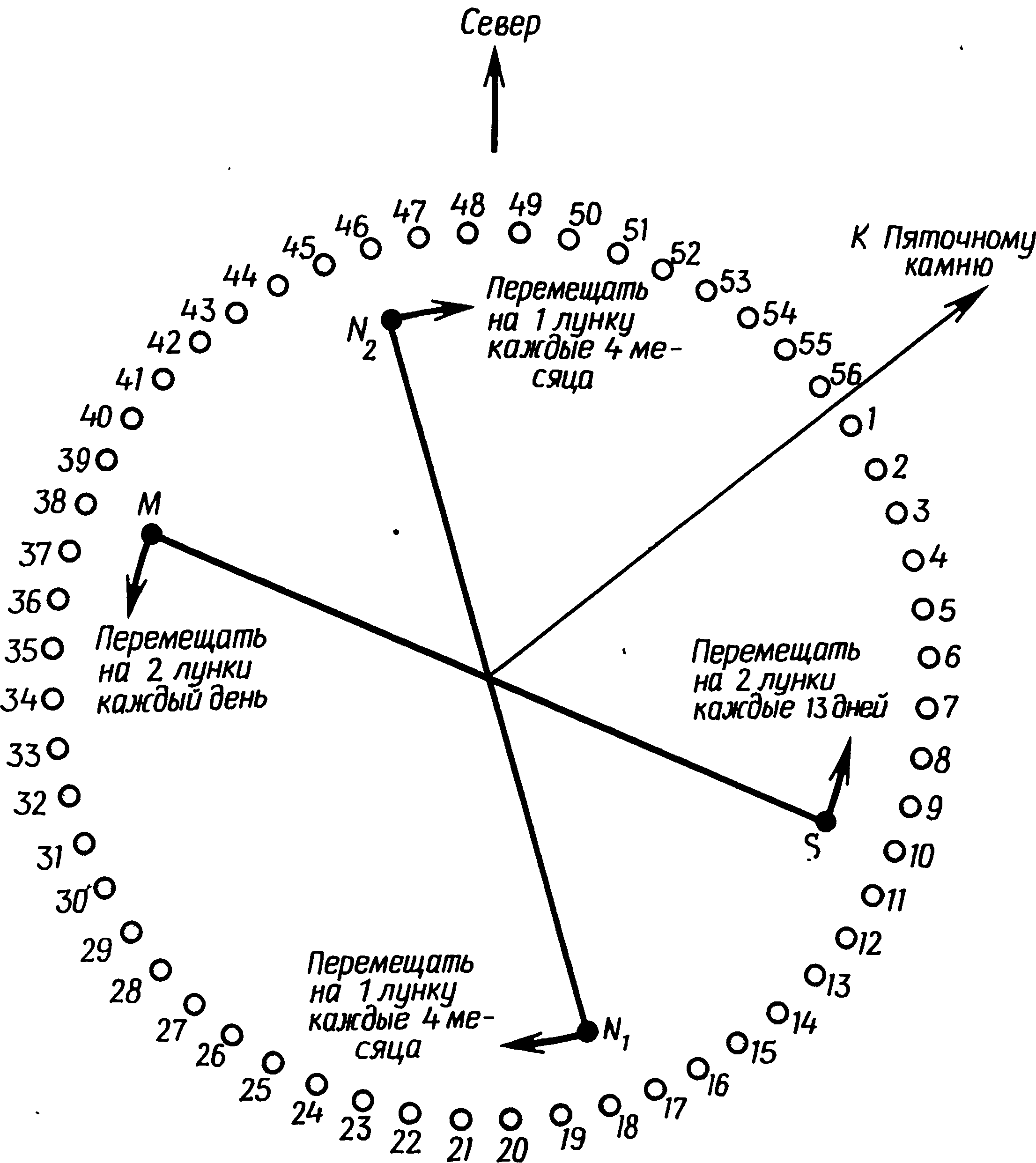
Через 223 синодических месяца Солнце, Луна и узлы лунной орбиты возвращаются почти точно в те же положения относительно друг друга. Если затмение произошло в какой-то определенный день, оно повторится 6585,32 суток спустя, т.е. через 18 тропических лет и 11⅓ суток. Оно повторится опять через 18 лет и 11⅓ суток и так далее. Затмения можно объединять в семейства, которые охватывают сотни лет. В табл. 4.3 есть много таких примеров: затмения 8 января 1917 г., 19 января 1935 г. и 29 января 1953 г. — все это полные затмения одного семейства. Затмения 3 марта 1923 г., 13 марта 1941 г. и 24 марта 1959 г. принадлежат к семейству затмений, выродившихся в частные. Последующие затмения одного семейства не всегда будут видимы из одной и той же точки земной поверхности, поскольку сарос не равен целому числу суток, а содержит лишние 0,32 суток. Этот остаток равен 7 часам 41 минуте, и каждое последующее затмение того же семейства происходит позже именно на такое время.

Существует еще много других циклов затмений, из которых наиболее любопытен цикл, содержащий 358 синодических месяцев, что соответствует 28 годам 345 дням. Неточность в этом цикле чуть менее часа, и он остается справедливым до 15 тысяч лет. Примеры двух повторений можно найти в табл. 4.3.

Здесь будет уместно рассмотреть то объяснение, которое дали лункам Обри в Стоунхендже Хокинс и Хойл. Хокинс указал, что три цикла по 18,61 года составляют 55,83 года и что в данный календарный день положение узлов будет почти точно таким же, как за 56 лет до этого. Поэтому и Луна взойдет почти точно в том же месте. Хокинс вывел из этого правило, что если полная Луна во время зимнего солнцестояния взойдет над Пяточным камнем, то будет затмение. Пяточный камень, как нам известно, примерно указывает направление на точку восхода Солнца в день летнего солнцестояния, и если полная Луна во время зимнего солнцестояния взойдет над ним, это значит, что она находится в середине промежутка между «высокой» и «низкой» Луной. Если в таком году произойдут затмения, они, несомненно, придутся на периоды зимнего и летнего солнцестояний.

Перемещая маркировочные камни по 56 лункам Обри на одну лунку в год, можно прослеживать положение Луны на протяжении цикла в 18,61 года и, следовательно, выявлять то время в году, когда затмения наиболее вероятны. Из табл. 4.3 мы видим, что 56-летний цикл верен для максимальных склонений полной Луны в период зимнего солнцестояния, но только для них. Он не приложим к цикличности для фаз Луны, которые повторяются через каждые 57 лет (три метоновых цикла), и не приложим к повторению затмений. Собственно говоря, метод Хокинса необходимо дополнять тщательными наблюдениями фаз Луны, и время от времени он дает неверные предсказания. Этот метод критиковали и на том основании, что для простого счета до 56 совершенно не требуется большого кольца лунок.

Согласно методу использования лунок Обри, предложенному Хойлом, их кольцо представляет собой схему эклиптики. Хойл говорит, что возле лунок можно помещать маркировочные камни для обозначения положения Солнца, Луны, восходящего и нисходящего узлов. Типичное их расположение изображено на рис. 4.11, где S и M — маркировочные камни для Солнца и Луны соответственно, а N₁ и N₂ — маркировочные камни для узлов. Камни S и M находятся точно друг против друга, потому что схема показывает, как были бы они размещены в полнолуние. Камень, обозначающий Солнце, каждые 13 дней перемещается против часовой стрелки на две лунки, совершая полный оборот за 364 дня, т. е. почти точно за год. Камень, обозначающий Луну, передвигается против часовой стрелки на две лунки каждый день, совершая полный оборот за 28 дней. Камни, обозначающие узлы, все время находятся на концах одного и того же диаметра и перемещаются на одну лунку каждые четыре месяца, совершая таким образом полный оборот за 18⅔ года. Это дает достаточно хорошие приближения для трех важных периодов. Если маркировочные камни с самого начала помещены в правильное положение, то каждый раз, когда S и M находятся друг против друга, а камни узлов — в тех же лунках, что и они, произойдет лунное затмение.

Этот метод лучше метода, предложенного Хокинсом, так как с его помощью предсказываются все затмения, не только лунные, но и солнечные. Для солнечного затмения требуется, чтобы камни, обозначающие Солнце и Луну, оказались в одной лунке и чтобы в той же лунке был камень N₁ или камень N₂. Найти исходное положение для камней S и M не так уж трудно, но отнюдь не ясно, каким образом строители Стоунхенджа могли бы правильно расположить камни узлов или корректировать их положение, когда они постепенно отклонились от правильного положения. Хойл выдвинул предположение, что они могли точно заметить время, когда «высокая» Луна достигла максимального склонения, а затем поместить маркировочный камень одного из узлов в лунку, которая была занята камнем Солнца S в день весеннего равноденствия. Однако в период «высокой» Луны определить момент наибольшего склонения очень трудно (вполне возможна ошибка на целый месяц) и проще было бы помещать камни узлов и делать для них поправки, ориентируясь по затмениям. Хотя этот метод изящен, он требует больших познаний и, по общему мнению, слишком уж сложен для неолитического периода.

Рис. 4.11. Метод, предложенный Хойлом для предсказания затмений с помощью лунок Обри

Есть и другие способы предсказания затмений, опирающиеся главным образом на прямые наблюдения и не требующие особых знаний о циклах затмений. Один из них — метод, предложенный профессором Томом. Он считает, что, произведя несколько действительно очень точных наблюдений мест восходов и заходов Луны, мегалитические астрономы могли бы обнаружить небольшие неправильности в ее движении, которые совпадают с «эпохами затмений». Мы вернемся к этому методу в гл. 6.

Простейший из предложенных до сих пор методов — метод Р. Колтона и Р. Мартина — опирается на регулярные, но несложные наблюдения восходов Луны. Полное затмение происходит, только когда Луна находится точно напротив Солнца. Если горизонт плоский, кольцо камней или других ориентиров, расположенных через правильные промежутки, может служить транспортиром, показывающим, когда точка восхода Луны находится как раз напротив точки захода Солнца. Луна каждый вечер восходит примерно на час позднее, и было бы несложно наблюдать последующие лунные восходы и следить, как они приближаются к нужному азимуту. Чтобы затмение было видимо в ночь полнолуния, Луна должна взойти незадолго — не более чем за полчаса — до захода Солнца. Если она взойдет слишком рано, затмение начнется только утром, когда Луна уже зайдет, а если она взойдет после захода Солнца, это будет означать, что затмение уже кончилось. Совпадение этих двух условий — необходимого азимута точки восхода Луны и необходимого времени ее восхода — позволит заранее знать, не только произойдет ли лунное затмение, но и будет ли оно видимо из места наблюдения. Этот метод не требует наличия какого-то определенного числа камней или лунок, хотя чем больше будет число маркировочных объектов, расположенных через правильные промежутки, тем лучше. Лунки Обри прекрасно подходят для подобного рода наблюдений.

Доисторические люди, несомненно, были знакомы со звездами не хуже, чем с Солнцем и Луной. Обитатели северо-запада Европы, вероятно, объединяли звезды в определенные группы, т. е. в созвездия, и сочиняли о них легенды, как делали это люди древних цивилизаций во многих областях мира, от Вавилона до Китая. Но вопрос заключается в том, продвинулись ли ранние европейцы дальше описаний и мифологии и вели ли они систематические наблюдения звезд, как, по нашему убеждению, они наблюдали Солнце и Луну? Этого мы не знаем, но движение звезд по сравнению с движениями Луны чрезвычайно просто. Они каждую ночь восходят на востоке и заходят на западе, а их склонения, хотя и не абсолютно постоянные, изменяются настолько медленно, что кажется, будто звезды из ночи в ночь восходят и заходят в одних и тех же местах. Разумеется, восходят и заходят они не точно в одно и то же время, а примерно на 4 минуты раньше каждый вечер. Это объясняется тем, что мы ставим свои часы по Солнцу, а не по звездам. Тропический год состоит из 365,25 суток, но по отношению к звездам Земля за то же время делает 366,25 оборота. А потому звездные, или сидерические, сутки, как их называют, на 1:365,25, т.е. на 4 минуты короче, чем солнечные сутки.

Когда мы начинаем искать отмеченные камнями или иными ориентирами направления, указывающие на точки восхода и захода звезд в неолите и раннем бронзовом веке, мы сталкиваемся с проблемой, которой не существует для Солнца и Луны. Наклон земной оси на протяжении веков медленно уменьшается, но кроме того, ее концы еще описывают круги, делая один оборот за 26000 лет, — это так называемая прецессия. Вращение Земли можно сравнить с вращением волчка: все видели, как покачивается вращающийся волчок — его ось начинает описывать круги (прецессировать), когда его вращение замедляется. Прецессия земной оси, как и покачивание волчка, вызывается гравитационными силами.

Влияние прецессии можно представить себе зрительно, взглянув на рис. 4.3 и вообразив, что плоскость эклиптики неподвижна, а продолжение оси Земли вращается вокруг линии, перпендикулярной эклиптике. В результате небесный экватор смещается относительно эклиптики, и при этом меняется его положение в пространстве. Положение звезд по отношению к эклиптике остается неизменным, но, поскольку мы измеряем все склонения от небесного экватора, относительно него они должны постоянно изменяться. И действительно, склонение каждой звезды испытывает колебания в пределах 47° (т.е. 2ε) с периодом 26 000 лет. За последние 4000 лет склонение всех звезд изменилось не менее чем на 5° и вплоть даже до 20°. Исследователь, который ищет направления на звезды в прошлом, должен начать с вычисления склонения ярчайших звезд для выбранной эпохи. Изложение математических методов такого вычисления выходит за рамки данной книги, но его можно найти в учебниках астрономии.

Хотя прецессия не изменяет заметно положения звезд от ночи к ночи, она тем не менее происходит достаточно быстро для того, чтобы звездные направления успели устареть на протяжении человеческой жизни. За 50 лет направление на точку восхода особенно быстро смещающихся звезд изменится на 0,5°, и один этот факт заставляет усомниться в разумности попыток отмечать точки восхода и захода звезд с помощью долговечных каменных сооружений.

Существует еще и сложность, связанная с трудностью наблюдения звезд близ линии горизонта. Лучи, касательные к поверхности Земли, в значительной степени поглощаются атмосферой — вот почему мы можем смотреть на заходящее Солнце без вреда для глаз. Заходящие звезды постепенно тускнеют и становятся совершенно невидимыми еще на высоте нескольких градусов над линией горизонта. Согласно личным наблюдениям профессора Хокинса, даже самая яркая из звезд Сириус, при восходе над ясным морским горизонтом различается только с большим трудом. Наименьшая высота, на которой звезда еще видна — угол угасания, — зависит не только от яркости самой звезды, но и от атмосферных условий.

Профессор Том отыскал около 50 памятников, где он обнаружил визирные линии, соответствующие точкам восхода или захода различных звезд между 2100 и 1500 гг. до н. э. Но без подтверждений независимым датированием эти направления носят чисто умозрительный характер; изменения склонения на протяжении рассматриваемого периода достигают нескольких градусов, и возможны совпадения звездных направлений с очень многими из отмеченных азимутов. В одной из своих статистических проверок профессор Том взял ряд предполагаемых направлений и вывел по ним углы угасания для различных дат в раннем бронзовом веке. Этот метод имеет так мало независимых подтверждений, что не может быть убедительным. Предположение о существовании звездных направлений становится еще более сомнительным вследствие того, что позже профессор Том стал приписывать некоторые из направлений склонениям Солнца для дат, промежуточных между солнцестояниями и равноденствиями. Возможно, о многом говорит и тот факт, что профессор Том не нашел ни одного несомненного направления, связанного с Сириусом, несмотря на то что Сириус много ярче других звезд. Если направления, связанные со звездами, действительно существовали, мы, естественно, должны были бы обнаруживать их для наиболее ярких звезд, заходящих за высокий видимый горизонт.

Ни один из этих доводов не исключает использования звезд по ночам для определения времени или даже в качестве вспомогательного средства для предсказания смены времен года. Календарь древних египтян опирался на гелиакальный восход Сириуса, т. е. на ежегодное первое появление этой звезды перед самым рассветом в восточной части неба после того, как она некоторое время не была видна, так как находилась слишком близко к Солнцу. Такое использование Сириуса не требовало ориентиров, отмечающих точки ее восхода на линии горизонта, а потому археологических следов не оставило. Мы знаем о том, как делали это египтяне, из письменных памятников. И никогда не сможем узнать, имелось ли что-либо подобное у обитателей северо-западной Европы в неолитический и ранний бронзовый периоды.