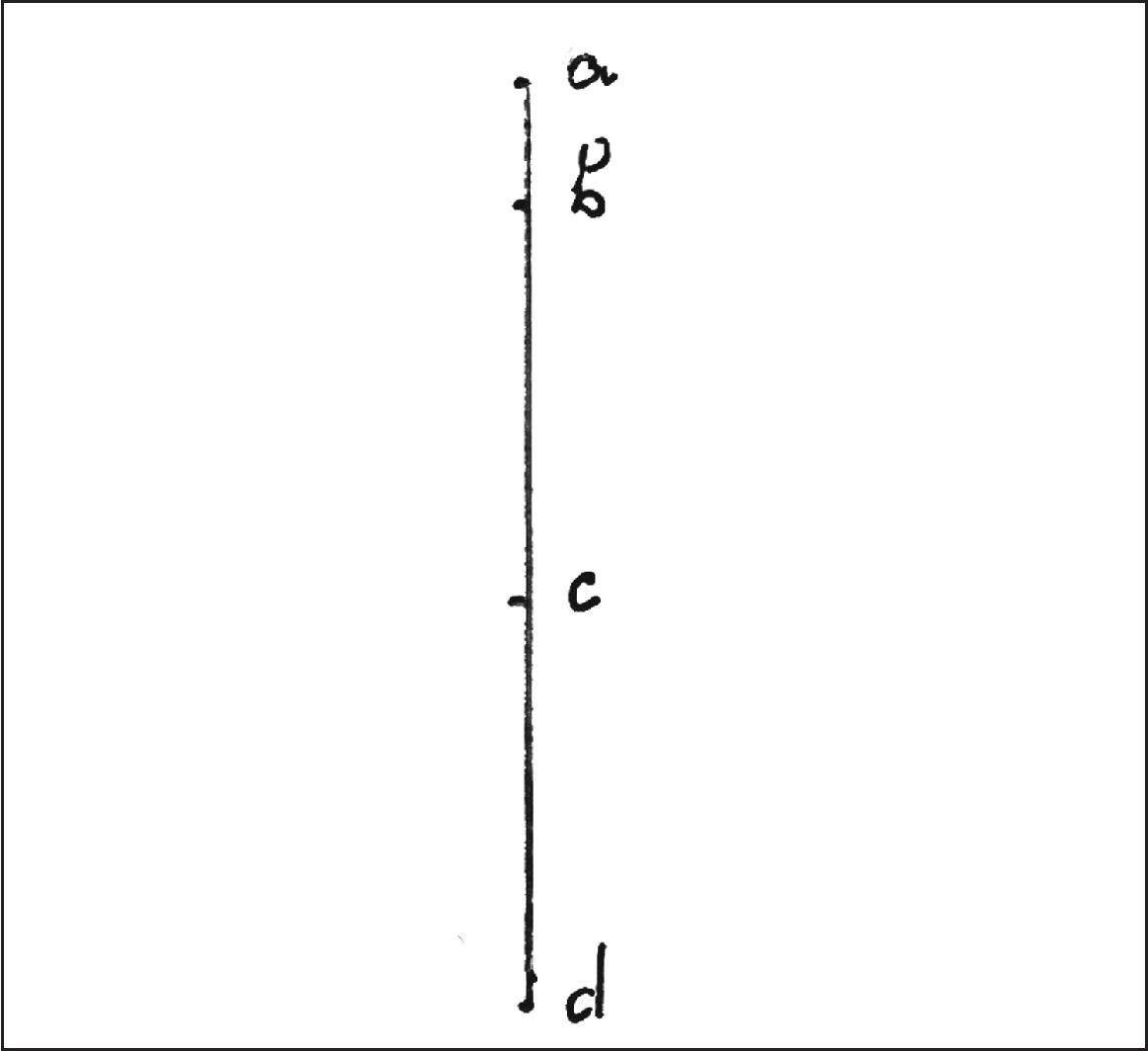
Письмо Галилея Паоло Сарпи

Прорыв в понимании Галилеем равноускоренного движения произошел, по-видимому, около 1604 г. В письме П. Сарпи от 16 октября этого года Галилей формулирует некоторые важные выводы: «Вновь размышляя о вопросах движения, — где мне недоставало для демонстрации наблюдавшихся мною явлений твердого принципа, который мог бы быть положен в качестве аксиомы, — я обратился к предположению, вполне естественному и очевидному и, приняв его, доказывал затем всё остальное, а именно: что отношение между пройденными в естественном движении путями такое же, как квадрат отношения между временами, и следовательно, пути, проходимые в равные времена, относятся друг к другу как нечетные числа, начиная с единицы, и прочие вещи. Принцип этот таков: скорость естественно движущегося [тела] возрастает пропорционально возрастанию расстояния тела от начала его движения. Я допускаю, что степень (иногда переводят — градус. — И.Д.) скорости, которую тяжелое тело, падающее, к примеру, из точки a вдоль линии abcd (рис. 15), имеет в [точке] c, так относится к степени его скорости в [точке] b, как расстояния ca к ba, и следовательно, в [точке] d тело имеет степень скорости настолько большую, чем в [точке] c, насколько da больше, чем ca.

Я бы хотел, чтобы Ваше Преподобие поразмышляли немного об этом и сообщили мне свое мнение. И если мы этот принцип принимаем, то мы тогда не только сможем доказать и все прочие утверждения, как я уже сказал, но и, как я полагаю, у нас в руках будет всё, чтобы показать, что и естественно падающее, и совершающее вынужденное движение подброшенное вверх тело проходят одни и те же отношения скорости»¹.

Рис. 15. Диаграмма из письма Галилея П. Сарпи от 16 октября 1604 г.

Как следует из сохранившихся рукописных заметок Галилея, датируемых 1601—1602 гг., он в это время проделал ряд экспериментов с целью разрешить некоторые вопросы, поставленные в «De Motu». Так, в письме Гвидобальдо дель Монте от 29 ноября 1602 г.² Галилей описывает свои опыты с маятниками и с движением тел по искривленным поверхностям, связывая их напрямую с рассмотренной в «De Motu» теоремой об «изохронности хорд» (см. далее)³. Кроме того, изучение ряда других архивных документов⁴ показало, что зафиксированные в них экспериментальные данные заставили Галилея отказаться от его прежнего понимания ускорения как некой «акциденции» естественного движения и начать рассматривать его как сущностную характеристику этого движения, а замедление — как сущностную характеристику движения вынужденного. По мнению Ю. Ренна, «если Галилей, основываясь на опыте, принял параболическую форму траектории (тела, брошенного под углом к горизонту. — И.Д.), он мог придти по крайней мере к интуитивной идее квадратичной зависимости расстояния от времени при свободном падении»⁵. В историко-научной литературе были предложены различные реконструкции хода исследований Галилеем ускоренного движения⁶. Однако, бесспорно, что два события (два инсайта) — признание, что траектория тела, брошенного под углом к горизонту, является параболической и принятие, пока в качестве гипотезы, (s ~ t²)-зависимости для свободного падения (где s — пройденный за время t путь) — оказались в галилеевых размышлениях о природе ускорения тесно связанными, хотя установить с полной уверенностью последовательность этих событий, видимо, невозможно, несмотря на обилие архивных документов.

Рис. 16. Диаграмма из рукописи Галилея MS, fol. 147r

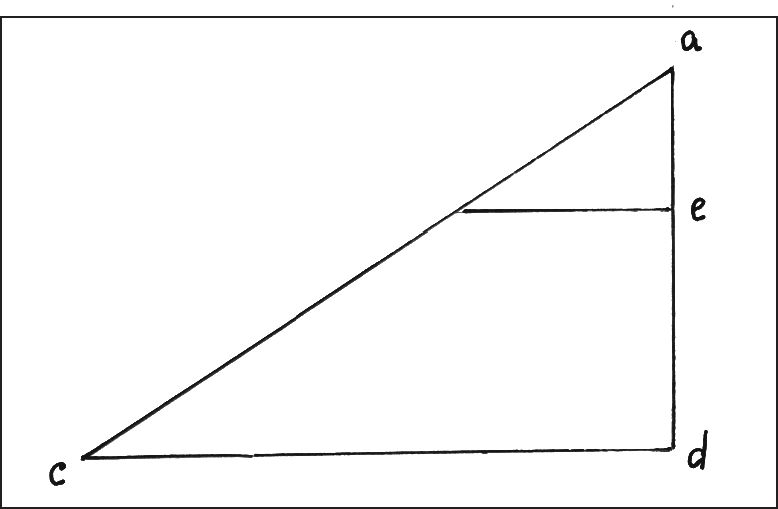
Но в любом случае (s ~ t²)-гипотеза требовала доказательства и экспериментальной проверки. С этой целью Галилей обращается к анализу своих экспериментов с качением шаров по наклонной плоскости. Его рассуждения и выводы зафиксированы в документе MS, fol. 147r⁷.

Галилей опирался на два утверждения. Согласно первому, времена свободного движения тела по хордам, проведенным из одной и той же точки окружности, равны (упомянутая выше теорема «изохронности хорд»), согласно второму — время свободного движения по вертикали ad (рис. 16) так относится к времени движения по ac, как длина ad относится к длине ac (далее, сокр. — lt-зависимость или lt-отношение). И кроме того, из теоремы об «изохронности хорд» Галилей сделал вывод о том, что «время [прохождения] по ad относится к времени [прохождения] по ac как ad относится к средней пропорциональной между ad и ae»⁸. Средняя пропорциональная величина между ad и ае в данном случае есть отрезок ax (на рис. 16 не обозначен) такой, что:

ad/ax = ax/ae, т. е. ax = √(ad·ae).

Таким образом, процитированное утверждение Галилея эквивалентно (s ~ t²)-теореме. Действительно, если

t_ad/t_ae = ad/√(ad·ae) (2),

то

t²_ad/t²_ae = ad/ae)

Сам Галилей, не очень склонный к использованию алгебраических методов и предпочитавший опираться на теорию пропорций, изложенную в «Началах» Эвклида, и геометрические доказательства, вывел (s ~ t²)-отношение из более сложных рассуждений. Но как бы то ни было, (s ~ t²)-зависимость была Галилеем почти доказана. Почти — потому что требовалось еще доказать справедливость lt-отношения, которое не могло быть выведено из теории движения, изложенной в «De Motu».

Поэтому Галилей обратился к поискам другого доказательства закона свободного падения, т. е. (s ~ t²)-закона, которое не использовало бы lt-отношение. Из текста цитированного выше его письма П. Сарпи видно, что к октябрю 1604 г. он уже имел в своем распоряжении этот закон и следовавшее из него «правило нечетных чисел» (ПНЧ)⁹. Однако при этом он держался того мнения, что увеличение «степеней (градусов) скорости» происходит в зависимости не от времени (V = V(t) в современных обозначениях), а от пройденного пути (V = V(s)).

Подобное толкование ускоренного движения сложилось задолго до Галилея¹⁰. Вот несколько примеров. «Чем дальше естественное движение от покоя, с которого оно начинается, — писал Эгидий Римский (Egidius Romanus; ум. в 1316 г.), — тем больше тело приближается к центру [мира], а потому его движение усиливается благодаря удалению от покоя...»¹¹. Дж. Б. Бенедетти, убежденный коперниканец, оказавший заметное влияние на Галилея, утверждал, что «чем оно [тело] дальше от начальной точки, тем оно быстрее [движется]»¹².

Кроме того, Галилей активно использовал учение об «интенсификации и ремиссии¹³ качеств» и концепцию «конфигурации качеств», с которыми, судя по его ранним рукописным заметкам¹⁴, а также по некоторым архивным документам (например, MS, fol. 107v), он был также хорошо знаком.

Примечания

1. Galilei G. Le Opere. Vol. X. P. 115.

2. Ibid. Vol. X. P. 97—100.

3. Ibid. Vol. VIII. P. 378. См. также: Wisan W.L. The New Science of Motion... P. 162—171; Galuzzi P. Momento... P. 266—267.

4. В частности, MS, fol. 107r-v, где Галилей анализирует движение тел по наклонным плоскостям, и рукописной заметки Г. дель Монте, касавшейся его наблюдений метательного движения, т. е. движения тела, брошенного под углом к горизонту, с которыми Галилей, по-видимому, был знаком и которые противоречили описанию этого движения, приведенному в «De Motu». См.: Naylor R.H. The Evolution of an Experiment: Guidobaldo del Monte and Galileo's Discorsi Demonstration of the parabolic trajectory // Physis. 1974. Vol. 16. P. 323—346; P. 327; Idem. Galileo's Theory of Projectile Motion // Isis. 1980. Vol. 71. № 259. P. 550—570; Drake S. Galileo's at Work... P. 86—90.

5. Damerow P., Freudenahl G., Mc Laughlin P., Renn J., Exploring the Limits... P. 152.

6. Кроме цитированной выше монографии (Damerow P., Freudentahl G., Mc Laughlin P., Renn J. Exploring the Limits...), см. также: Naylor R.H. The Evolution of an Experiment... P. 333; Hill D.K. Dissecting Trajectories: Galileo's Early Experiments on Projectile Motion and the Law of Fall // Isis. 1988. Vol. 79. № 299. P. 646—668; Drake S. History of Free Fall: Aristotle to Galileo. Toronto: Wall & Thomson, 1989. P. 35—49.

7. Galilei G. Le Opere. Vol. VIII. P. 380.

8. Galilei G. Le Opere. Vol. I. P. 380 (MS, fol. 147r). Я опускаю здесь приведенное Галилеем доказательство этого утверждения (см.: Damerow P., Freudentahl G., Mc Laughlin P., Renn J. Exploring the Limits... P. 157—158).

9. Действительно, если тело при равноускоренном движении проходит расстояние S₁ за время t₁, расстояние S₂ — за время 2t₁, а расстояние S_n — за время nt₁ и т. д., то, учитывая, что S_n ~ (nt_t)² и S_n+1 ~ [(n+1)t₁]², получаем S_n+1 - S_n = (2n+1) t₁².

10. На неправильность этого утверждения в литературе указывалось неоднократно (см., например: Max Э. Механика: историко-критический очерк ее развития / Пер. с нем. Г.А. Котляра, под ред. Н.А. Гезехуса. СПб: Общественная польза, 1909. С. 214; Григорьян А.Т., Зубов В.П. Очерки развития основных понятий механики. М.: Изд-во АН СССР, 1962. С. 152153). Если бы скорость возрастала прямо пропорционально проходимому пути, т. е. V = kS, то путь зависел бы от времени следующим образом: S = S₀e^kt и тогда, как заметил Л. Эйлер, «никакие тела не могли бы прийти в движение» (Euler L. Mechanica. Petropoli, 1736. Cap. 2, prop. 15, § 135. T. 1. P. 54).

11. Egidius Romanus, in octo libros Physicorum Aristotelis, I. VII, lectio 26. Venetia, 1502, fol. 217v. (Цит. по: Григорвян А.Т., Зубов В.П. Очерки... С. 108 (перевод В.П. Зубова).

12. Цит. по: Григорьян А.Т., Зубов В.П. Очерки... С. 108 (перевод В.П. Зубова).

13. Иногда переводят — «интенсии и ремиссии».

14. Galilei G. Le Opere. Vol. I. P. 119. См. подр.: Wallace W.A. Galileo's early notebooks: the physical questions / Transl. from the Latin, with historical and paleographical commentary. Notre Dame, Ind.: University of Notre Dame Press, 1977. P. 172; Sylla E. Galileo and the Oxford Calculatores: Analytkal Languages and the Mean-Speed Theorem for Accelerated Motion // Reinterpreting Galileo / Ed. by W.A. Wallace. Washington: Catholic University of America Press, 1986. P. 53—108.