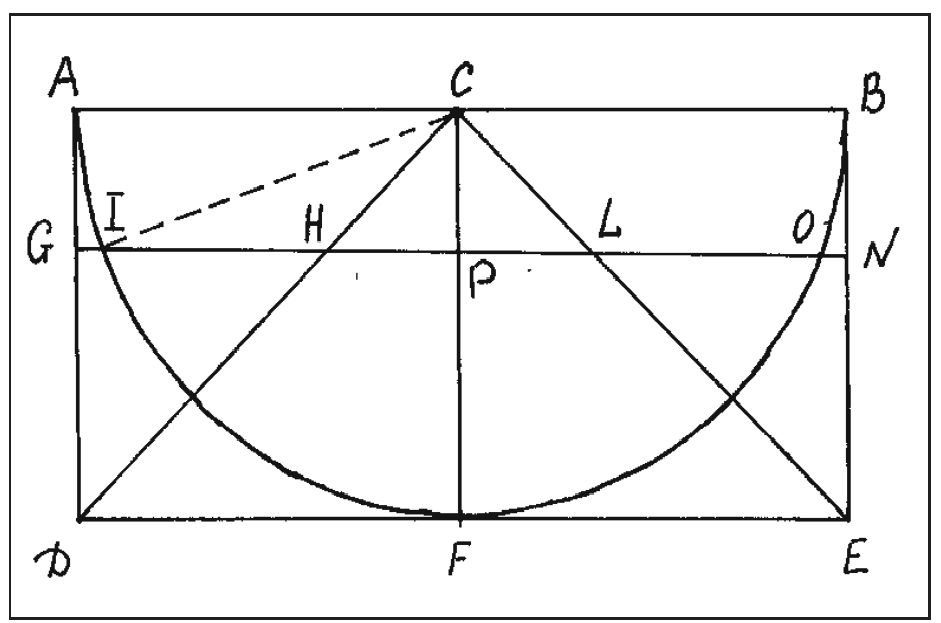
Элейские трудности, или Парадоксы «инфинитезимальной атомистики»

Как правило, анализируя полемику Первого дня «Dialogo», историки науки трактуют ее содержание как свидетельство рождения новой науки, науки Нового времени, акцентируя внимание на глубоких отличиях галилеевых взглядов от традиционных перипатетических. Впрочем, некоторые авторы справедливо указывают на сложность и неоднозначность соотнесенности позиций Галилея и Аристотеля¹, тогда как другие, начиная с П. Дюгема, подчеркивали глубокую преемственность («continuity») между механикой Галилея и концепциями «калькуляторов» XIV столетия² и научными достижениями математиков и астрономов ордена Иисуса, а также укорененность общеметодологических воззрении итальянского ученого в платонизме³. Такое многообразие выявляемых историко-научной мыслью идейных предтеч Галилея вполне закономерно, поскольку интеллектуальная революция XVI—XVII вв. возникла в результате «резонанса» различных традиций и «социальных эстафет» (М.А. Розов).

Первый день «Диалога» начинается с обсуждения одного высказывания Аристотеля, приведенного «в его общем рассуждении, связанном со всеобщим и первыми началами»⁴. Речь идет об утверждении Стагирита о том, что отсутствие тяжести и легкости, нетленность, извечность, неподверженность «никаким изменениям, кроме перемены места, и т.д. — все эти состояния присущи телу простому и движущемуся круговыми движениями, а противоположные свойства: тяжесть, легкость, тленность и т. д., он [Аристотель] приписывает телам, естественно движущимся прямолинейным движением»⁵. Иными словами, вопрос касался фундаментального различия между двумя типами естественных движений — прямолинейного и движения по окружности, а также между двумя видами прямолинейных движений: 1) восходящим и нисходящим (sursum et deorsum) и 2) вынужденным.

Сальвиати, выступающий от лица Галилея, упрекает греческого мыслителя в том, что тот «начал свое рассуждение превосходно и методически, но, имея в виду скорее достигнуть некоторой конечной цели, заранее установившейся у него в уме, чем прийти туда, куда прямо вел весь ход рассуждения, прервал нить его...»⁶. И вообще — на этот раз упрек исходит от Сагредо — «можно подумать, что он [Аристотель] намеренно подтасовывает карты в игре и хочет приладить план к мирозданию, а не построить это здание по указаниям плана»⁷. Сальвиати подхватывает его мысль — «всякий раз, как в основном положении обнаруживается какая-нибудь ошибка, можно с полным основанием сомневаться и во всем остальном, как воздвигнутом на этом фундаменте»⁸, а потому Сальвиати надеется в ходе дальнейшего диалога, «направляясь иным путем, выбраться на более прямую и надежную дорогу и заложить основной фундамент, более считаясь с правилами строительства»⁹. После этой декларации о намерениях собеседники переходят к конкретным вопросам механики, и тут же все оказывается много сложней и драматичней, чем ожидалось.

Сальвиати начинает с того, что прямолинейное движение вообще не может существовать в хорошо упорядоченном мире и невозможно по природе, а в том, что наш мир «необходимо должен быть <...> в высшей степени упорядоченным, т. е. в отношениях его частей должен господствовать наивысший и наисовершеннейший порядок»¹⁰, никто из участников диалога не сомневался. После этого он формирует главный тезис (критика Аристотеля пока оставлена в стороне), слышанный им «от нашего общего друга из Академии dei Lincei»¹¹ (т. е. от самого Галилея): «Всякое тело, которое, по какой-либо причине, находится в состоянии покоя, но по природе своей подвижно, оказавшись свободным, придет в движение при условии, что оно от природы, обладает влечением к какому-нибудь определенному месту; ибо если бы оно было безразлично по отношению ко всякому месту, то пребывало бы в покое, не имея большего основания (я бы перевел — большей причины. — И.Д.) двигаться к одному месту, чем к другому. При наличии же такого влечения тело необходимо (точнее было бы перевести — естественно. — И.Д.) движется с непрерывным ускорением»¹².

На минуту прервем цитирование. Итак, Сальвиати утверждает, что причина движения тела состоит в его естественном стремлении («влечении», inclinatio) к некоторому месту и вызванное этим «влечением» движение является ускоренным. Сразу обращает на себя внимание то обстоятельство, что приведенная формулировка как-то не вяжется с образом Галилея как (перво)открывателя закона инерции. Далее я рассмотрю этот вопрос более детально, а пока ограничусь простой констатацией: из сказанного до сих пор Сальвиати вытекает задача исследователя — дать причинное объяснение как ускоренного, так и равномерного движения. С этой целью Сальвиати — продолжу цитирование — предлагает несколько для его собеседников неожиданное (чтобы не сказать сильнее) рассуждение: тело движется («естественным влечением») «с непрерывным ускорением, начиная с самого медленного движения, оно достигнет некоторой степени скорости не раньше, чем пройдя все степени меньших скоростей или, скажем, больших медленностей, ибо при отправлении от состояния покоя (который есть степень бесконечной медленности движения) у тела нет никакого основания достигнуть той или иной определенной степени скорости, прежде чем оно не пройдет меньшую степень, а также степень ещё меньшую, прежде чем достигнет этой последней; напротив, есть вполне достаточные основания к тому, чтобы тело прошло сперва степени, соседние по отношению к той, от которой оно идет, а потом более отдаленные; но степень, с которой движущееся тело начинает двигаться, есть степень наивысшей медленности, т. е. покой»¹³.

На недоумение Сагредо — каким образом телу за конечное, притом кратчайшее время удастся пройти «все предварительные степени медленности (т. е. скорости. — И.Д.) <...>, каковых степеней бесконечное множество»?¹⁴ — Сальвиати отвечает: «движущееся тело проходит через все названные степени, но при этом переходе не задерживается ни на одной из них; таким образом, если этот переход требует не больше одного момента времени, а сколь угодно малое время содержит бесконечное количество моментов, мы всегда можем связать каждый момент с соответствующей из бесконечных степеней медленности, как бы кратко ни было это время»¹⁵.

Это рассуждение первого дня «Dialogo», касающееся природы континуума¹⁶, получило затем развитие в аналитике первого дня «Discorsi». Поскольку эта проблематика уже неоднократно была предметом историко-научного и философского анализа¹⁷, я остановлюсь здесь только на узловых моментах галилеевой концепции природы континуума¹⁸. Речь идет о бесконечности самих конечных предметов, например, о представлении окружности как правильного n-угольника «с бесконечно большим числом сторон»¹⁹, т. е. когда n → ∞ и каждая сторона обращается в точку.

Рассуждения Сальвиати вызывают недоумение у перипатетика Симпличио: «это составление линии из точек, делимого из неделимого, конечного из неконечного кажется мне нелегко преодолимым препятствием»²⁰. В ответ Сальвиати конструирует новые парадоксы и изобретает новые головоломки, усиливая тем самым парадоксальность ситуации, желая продемонстрировать «как иной раз удивительные вещи бледнеют перед лицом чудесных»²¹. К примеру, он предлагает мысленный «геометрический эксперимент», в котором две одинаковые поверхности и два одинаковых (равновеликих) тела, поставленные на эти поверхности, как на основания, постепенно уменьшаются. При этом по мере уменьшения тел их равновеликость сохраняется. В итоге — «в последний момент», «в конце концов» — одно тело вместе со своей поверхностью трансформируется в линию, т. е. в бесконечное множество точек, а другое — в одну-единственную точку²².

Рис. 28. Из книги Галилея «Беседы и математические доказательства...»

Все сказанное Сальвиати-Галилеем — и в «Dialogo», и в «Discorsi» — нацелено на то, чтобы через осмысление процедур построения конечного (отрезка линии или ограниченной поверхности) из бесконечного числа единиц и через соединение — по необходимости — в одном решении двух по отдельности неразрешимых задач («изучить одновременно и бесконечное, и неделимое»²³), показать невозможность освоения «бесконечности мира в конечном человеческом разумении»²⁴. Иными словами, Сальвиати показывает, что при переходе от конечного и делимого к бесконечному и неделимому происходит — «в конце концов», «в последний момент» — некая скрытая трансформация рассматриваемых объектов, которая делает нашу обычную, стандартную аристотелеву логику неприменимой, и что игнорирование ограниченности этой логики ведет к парадоксальным следствиям.

Поэтому когда ошарашенный Симпличио заявляет, что «признание одной бесконечности большей, нежели другая бесконечность представляется непостижимым», Сальвиати ему разъясняет: все затруднения происходят «вследствие того, что, рассуждая нашим ограниченным разумом о бесконечном, мы приписываем последнему свойства, известные нам по вещам конечным и ограниченным»²⁵, тогда как «свойства равенства, а также большей и меньшей величины, не имеют места там, где дело идет о бесконечности»; более того²⁶, Сальвиати ставит под вопрос сами понятия «составить» и «построить из», когда речь идет о бесконечном. «Да, составите конечное из бесконечных частей, образовать делимое из неделимых невозможно. Этот процесс бесконечен, в нем мы все больше приближаемся к целому, но никогда его не достигнем. Но по способу бытия (а не формирования) конечное и делимое состоит из неделимых и бесконечных, точнее, оно есть целостное, неделимое, бесконечное. И в этом смысле к конечному, понятому как бесконечное, к делимому, понятому как неделимое, неприменимы те обычные понятия, которые мы употребляем по отношению к конечным и делимым вещам, линиям, плоскостям»²⁷.

Используемая Сальвиати-Галилеем процедура «объяснения» удивительного через чудесное ведет к тому, что удивительное становится заурядным, поскольку для своей области, т. е. для открытого в приведенных рассуждениях нового мира — оно есть правило. С помощью традиционной логики Сальвиати-Галилей показывает, что эта логика не универсальна, она ограничена миром конечных величин. «Заблуждается тот, — предостерегает он Симпличио и читателей, — кто желает наделить бесконечное теми же атрибутами, которые присущи вещам конечным, в то время как эти две области по природе своей не имеют между собой ничего общего»²⁸.

По ходу полемики её участники выявляют очень важный аспект темы. Отвечая на замечания Симпличио — мол, рассуждения Сальвиати чисто математические и к физической реальности отношения не имеют и «не так легко будет разделить линию (отрезок. — И.Д.) на бесконечное множество точек» (это разделение так и «останется одной из тех возможностей, которые никогда не осуществляются»²⁹), — последний (Сальвиати) соглашается с тем, что, действительно, никакая последовательная — т. е. шаг за шагом осуществляемая операция, когда отрезок прямой сначала делится пополам, затем на четыре части, затем на восемь и т. д., и т. д. не приведет к получению бесконечного множества точек (актуальной бесконечности), поскольку «такой процесс постепенного деления конечных величин необходимо было бы продолжать вечно»³⁰, однако это можно сделать иначе, трансформируя n-угольник в круг. «Если, — продолжает Сальвиати, обращаясь к Симпличио, — сгибание линии под углами так, чтобы образовался квадрат, или восьмиугольник, или многоугольник с сорока, ста или тысячью сторонами, представляется вам достаточным для действительного выявления тех четырех, восьми, сорока, ста или тысячи частей, которые, как вы говорите, содержались потенциально в первоначальной прямой линии, то, когда я образую из прямой линии многоугольник с бесконечным числом сторон, т. е. когда я сгибаю её в окружность, не могу ли я с таким же правом утверждать, что я вызываю к действительности то бесконечное множество частей, которое первоначально, пока линия была прямой, содержалось в ней в потенции?»³¹

Иными словами, Сальвиати убеждает собеседников в том, что хотя процедура получения инфинитезимальных сущностей путем последовательных делений целого на части не реализуема, однако актуальный бесконечно малый компонент целого (континуума) в итоге всё-таки достижим путем, как выразился З. Бехлер, «infinitesimal atomisation of the continuum»³², если «раздроблять и разделять бесконечность (tutta la infinita) одним разом»³³, когда физический континуум в пределе переходит в определения континуума математического, т. е. когда точки определяются двояко — как абсолютно непротяженные и как материальные, существующие исключительно в действии «на другое» (как точки соприкосновения тел, «удара» и т. д.). Таким образом оказывается, что отрезки прямой, окружности и т. п. объекты обретают двоякий статус — они суть объекты и геометрические, и физические, существующие и действующие в рамках «an unified, mathematico-physical ontology»³⁴, а потому не являющиеся в полном смысле ни физическими, ни геометрическими, но и теми, и другими одновременно. К этим новым, пограничным, limbo-сущностям (если воспользоваться терминологией З. Бехлера) применимо понятие «равенство в пределе».

«То, что происходит с телами, — подытоживает Сальвиати рассмотрение описанного в сноске 557 парадокса последовательного уменьшения равновеликих тел (конуса и полусферы), — имеет место и в отношении площадей их оснований, сохраняя при постоянном уменьшении равенство между собою, они переходят в последний момент (т. е. в пределе. — И.Д.) — одна в окружность, другая в точку. Так почему же мы не можем назвать их равными, когда они являются последними остатками и следами неизменно равных величин?»³⁵ Но это означает, что термин равенство величин, как и термины «больше чем», «меньше чем» и «отношение», получают новый, нетрадиционный смысл.

В итоге ограниченность традиционной, аристотелевой логики оказывается обусловленной существованием нетрадиционных limbo-сущностей. На вопрос Сальвиати — конечно или бесконечно «число конечных частей [ограниченного] континуума (parti quante)»³⁶, Симпличио отвечает, что «их число и бесконечно, и конечно: бесконечно — потенциально, конечно — актуально», поскольку «нельзя себе представить частей самих по себе, пока они не отделены или, по крайней мере, не обозначены; в противном случае они будут, так сказать, лишь потенциальными»³⁷. Именно так и должен был ответить последовательный аристотелианец, для которого конечный континуум может содержать только конечное число конечных частей, а ссылка не бесконечность частей предполагает актуальность бесконечного деления. Для Галилея же число частей ограниченного континуума не конечно и не бесконечно численно, но соответствует любому наперед заданному числу³⁸. Но тогда аристотелево различение между «актуальным» и «потенциальным» разделением этого континуума на части лишается смысла, поскольку в конечной величине, согласно Галилею, не может содержаться бесчисленного множества частей ни актуально, ни потенциально, и, следовательно, нет различия между актуальностью и потенциальностью деления ограниченного континуума и бесконечное оказывается актуальным, оно есть число неделимых точек, которые составляют конечный континуум.

«Я готов согласиться с философами — заявляет Сальвиати, — что непрерывное целое содержит столько частей, сколько им будет угодно, и содержит эти части по их желанию актуально или потенциально. Но к этому я добавляю: совершенно так же, как линия в десять сажен содержит в себе одновременно десять линий по одной сажени каждая, сорок линий по локтю каждая, восемьдесят — по полулоктю и т. д., она содержит и бесконечное множество точек, и вы можете сказать — актуально и потенциально, как вам будет угодно»³⁹.

Существование актуальной бесконечности неделимых в конечном континууме выводится Сальвиати-Галилеем из факта бесконечной делимости этого континуума. Галилею, конечно, известно, что аристотелианцы из этого же факта делали прямо противоположный вывод — неделимых не существует, ибо в противном случае деление имело бы конец. Но у Галилея свои резоны: «так как линия, как и всякий континуум, может быть разделена на части, также далее делимые, то нельзя избежать заключения, что линия состоит из бесконечного множества неделимых, потому что, предполагая возможность бесконечно продолжать деление, мы получаем и бесконечное множество частей; иначе деление могло бы прийти к концу, а если частей бесконечно много, то нельзя не прийти к заключению, что они не конечны, так как бесконечно много конечных величин дает величину бесконечно большую; таким образом, мы имеем континуум, составленный из бесконечного множества неделимых»⁴⁰, т. е. из бесконечного множества элементов, лишенных величины⁴¹, можно составить сколь угодно большое тело.

Этот вывод послужил необходимой предпосылкой для следующего утверждения: любая конечная величина состоит из актуальных частей до того, как эти части разделены (вспомним, что Симпличио декларировал прямо противоположное: «нельзя представить частей самих по себе, пока они не отделены или, по крайней мере, не обозначены»). Это столкновение двух предпосылок — аристотелевой и платоновой — ясно обозначено Галилеем в кратких репликах, которыми обменялись Симпличио и Сальвиати:

«Симпличио: Но если мы можем постоянно производить деление на части конечные, то какая надобность нам вводить здесь не конечные?

Сальвиати: Самая возможность постоянного разделения на конечные части приводит к необходимости признать, что целое состоит из бесконечно многих не конечных частей (di infiniti non quanti)»⁴².

Если потенциальная бесконечность всегда предполагала бесконечное множество, составленное из чего-то конечного — будь то числа, промежутки времени, области пространства и т. д., (т. е. предполагалось, что конечный континуум содержит конечное число конечных частей, а ссылка на бесконечность частей означает лишь актуальность бесконечного деления), то бесконечность актуальная предполагала предельный переход в иное качество, к иной сущности.

«Части, — писал Галилей, — имеющиеся в отрезке линии, не могут быть конечны, так как деление не может прекратиться ранее бесконечности; не могут быть бесконечны, так как в таком случае заданная линия была бы бесконечно длинной. Я утверждаю, что они не бесконечны и не конечны, а лишь таковы, что отвечают всякому числу; но, отвечая всякому числу, они не бесконечны, потому что никакое число не бесконечно; но в еще большей мере они и не конечны, т. е. не определены каким-либо числом, так как для любого определенного числа всегда существуют другие, большие, чем оно. Обман состоит в словесном противопоставлении: либо они конечны, либо бесконечны; так как "конечный" и "бесконечный" — понятия неоднородные, то самое деление неправильно. Нельзя утверждать, что слоновая кость либо желтая, либо сладкая, так как она может быть ни желтой, ни сладкой. 1000 не ближе к бесконечности, чем 100, или чем 20, или чем 4; и путь от 4 к 20 и от 20 к 100 и к 1000 и т. д. не ведет к бесконечности. Поэтому такое исследование не может выяснить вопрос, существует ли бесконечность или нет <...>. То, что отвечает всем числам, не должно быть вовсе бесконечным, а то, что определено каким-нибудь числом, не отвечает всем числам, так как никакое число не заключает в себе все числа. <...>. Итак, мы имеем три различные вещи: то, что определено каким-либо числом, то, что отвечает всем числам, и бесконечность. Тот, кто скажет, что части непрерывного таковы, что отвечают всем числам, скажет правильно.

Бесконечность же должна быть вовсе исключена из математических рассуждений, так как при переходе к бесконечности количественное изменение переходит в качественное, подобно тому, как если мы будем самой тонкой пилой (sotilissima lima) размельчать тело, то, как бы мелки ни были опилки (minutissima polvere), каждая частица имеет известную величину, но при бесконечном размельчении получится уже не порошок, а жидкость, нечто качественно новое, причем отдельные частицы вовсе исчезнут»⁴³. Таким образом, в анализе «головоломок», предложенных Сальвиати, осмысливался парадокс «такого доведения до предела физического континуума, в котором он переходит в определения континуума математического и обратно»⁴⁴.

Если теперь вернуться к проблеме движения, взглянув на неё через призму очерченного выше галилеева анализа проблемы бесконечного и неделимого, то оказывается, что тело падает с бесконечной степенью ускорения, только если представить, будто оно движется толчками, задерживаясь в каждой точке, а не проходя непротяженные точки «без остановки». «Благодаря возможности делить время без конца» можно придти «к любой малой степени скорости» путем непрерывного ее (скорости) уменьшения⁴⁵, и тогда можно сказать, что ускоряющееся тело «только проходит через эти степени, не задерживаясь больше, чем на мгновение; а так как в каждом, даже в самом малом промежутке времени содержится бесконечное множество мгновений, то их число является достаточным для соответствия бесконечному множеству уменьшающихся степеней скорости»⁴⁶. Иными словами, речь идет о том, что сумме бесконечно большого числа бесконечно малых отрезков времени соответствует сумма бесконечно большого числа «мгновенных скоростей». И понятие «мгновенной скорости», равно как и понимание всякой скорости как бесконечной суммы мгновенных скоростей — отнюдь не «как бы магическое заклинание», с помощью которого совершается прыжок от вневременных мгновений к времени, от внепространственных неделимых к пространству, от «неподвижных составляющих» движения к самому движению⁴⁷, но актуальное состояние тела.

Хотя мгновенная скорость не характеризует актуальное конечное расстояние, пройденное телом за конечный промежуток времени, она всё же характеризует «точечную» интенсивность движения, интенсивность движения в данный момент времени, которая с течением времени изменяется, ибо в каждый момент падающее тело находится в ином состоянии движения, чем в предыдущий.

Примечания

1. См., например: Damerow P., Freudentahl G., MacLaughlin P., Renn J., Exploring the Limits... Как заметила Р. Фельдхей, «Проект Галилея можно рассматривать как синтез идей Аристотеля и Архимеда, синтез, который нарушал основные правила обоих дискурсов» (Feldhay R. The use and abuse of mathematical entities: Galileo and the Jesuits revisited // Cambridge Companion to Galileo / Ed. by P. Machamer. Cambridge: Cambridge University Press, 1998. P. 80—146; P. 104).

2. Wallace W.A. Galileo and His Sources...; Wallace W.A. Prelude to Galileo: Essays on Medieval and Sixteenth-Century Sources of Galilleo's Thought. Boston etc.: Kluwer Academic Publishers, 1981; Sylla E. Galileo and the Oxford Calculatores...; Wolff M. Impetus Mechanics as a Physical Argument for Copernicanism: Copernicus, Benedetti, Galileo // Science in Context. 1987. Vol. 1. № 2. P. 215—256; Carugo A., Crombie A.C. The Jesuits and Galileo's Ideas of Science and Nature // Annali del Museo di Storia della Scienza di Firenze. 1983. T. VIII. P. 1—68.

3. Koyré A. Galileo and Plato // Roots of Scientific Thought / Ed. by P. Wiener and A. Noland. New York: Basic Books, 1957. P. 147—175; Galluzzi P. Il Platonismo del Tardo Cinquecento e la filosofia di Galileo // Ricerche sulla Cultura dell'Italia Moderna / Ed. by P. Zambelli. Bari: Laterza, 1973. P. 39—79; De Caro M. Galileo's Mathematical Platonism // Philosophie der Mathematik / Hrsg. J. Czermak. Wien: Hölder-Pichler-Tempsky, 1993; Bechler Z. Newton's Physics and the Conceptual Structure of the Scientific Revolution. Dordrecht; Boston; London: Kluwer Academic Publishers, 1991. Chapter VI.

4. Галилей Г. Диалог... С. 115.

5. Там же.

6. Там же. С. 114.

7. Галилей Г. Диалог... С. 112.

8. Там же. С. 115.

9. Там же.

10. Там же.

11. Там же. С. 117.

12. Там же. Курсив мой. — И.Д.

13. Галилей Г. Диалог... С. 117.

14. Там же. С. 118.

15. Галилей Г. Диалог... С. 118.

16. И примыкающее к содержанию известных апорий Зенона Элейского («Стрела», «Ахиллес и черепаха» и «Дихотомия»), рассмотренных затем Аристотелем.

17. Smith A.M. Galileo's theory of indivisibles: Revolution or Compromise? // Journal of the History of Astronomy. 1976. Vol. 37. № 4. P. 571—588; Bechler Z. Newton's Physics... Chapter VI; Библер В.С. Галилей и логика мышления Нового времени // Механика и цивилизация XVII—XIX вв. / Под ред. А.Т. Григорьяна и Б.Г. Кузнецова. М.: Наука, 1979. С. 448—518; Гайденко П.П. Эволюция понятия науки (XVII—XVIII вв.): формирование научных программ Нового времени. М.: Наука, 1987. С. 69—138.

18. При этом в целях экономии места я не буду детально описывать знаменитые головоломки и парадоксы, изложенные в первом дне Discorsi (качение концентрических многоугольников и окружностей и др.). При желании читатель может обратиться к тексту этого сочинения Галилея, а также к перечисленной в предыдущей сноске литературе.

19. Галилей Г. Беседы... // Галилей Г. Избр. труды. Т. II. С. 135.

20. Там же. С. 136.

21. Там же. С. 137.

22. Галилей Г. Диалог... С. 137—138. Рассмотрим рис. 28. Полукруг AFB с центром C и описанный около него прямоугольный параллелограмм ADEB. От центра к точкам D и E проведены прямые линии CD и CE. Вся фигура вращается вокруг неподвижной линии CF. Прямоугольник опишет цилиндр, полукруг AFB — полушар, а треугольник CDE — конус. Полушар вынимается, а остается конус и «чаша» — часть цилиндра, выходящая за пределы полушара. Далее доказывается равновеликость чаши и конуса. Затем обе фигуры рассекаются плоскостью, параллельной основанию. Плоскость эта, где бы её ни провести, всегда отсекает два равных между собой тела — верхушку конуса и верхнюю часть чаши. Также остаются равными основания этих тел — упомянутая полоса и круг HL. Проводя секущую плоскость все выше и выше, мы все время получаем равные тела и основания. И, наконец, в последний момент (в вершине) большая окружность оказывается равной одной точке. В этот момент оба тела (всегда равные) и обе площади (всегда равные) перейдут — одно в окружность, другое — в точку. (См. также: Библер В.С. Галилей и логика мышления Нового времени... С. 499).

23. Галилей Г. Беседы... С. 139.

24. Библер В.С. Галилей и логика мышления Нового времени... С. 500.

25. Галилей Г. Беседы... С. 140.

26. Там же. С. 141.

27. Библер В.С. Галилей и логика мышления Нового времени... С. 500.

28. Галилей Г. Беседы... С. 145.

29. Галилей Г. Беседы... С. 144, 157.

30. Там же. С. 145.

31. Там же. С. 153.

32. Bechler Z. Newton's Physics... P. 532.

33. Bechler Z. Newton's Physics... P. 153.

34. Ibid. P. 133.

35. Галилей Г. Беседы... С. 138.

36. Там же. С. 142.

37. Галилей Г. Беседы... С. 142.

38. Там же. С. 143.

39. Там же. С. 144.

40. Галилей Г. Беседы... С. 142.

41. А потому — бестелесных, ибо тело всегда имеет какую-то величину (Гайденко П.П. Эволюция понятия науки (XVII—XVIII вв.)... С. 79.

42. Галилей Г. Беседы... С. 142.

43. Эта цитата из Pensieri varii (§ 18) Галилея взята мною из содержательной вступительной статьи С.Я. Лурье к русскому переводу трактата Б. Кавальери (Лурье С.Я. Математический эпос Кавальери // Кавальери Б. Геометрия, изложенная новым способом при помощи неделимых непрерывного, с приложением «Опыта IV» о применении неделимых к алгебраическим степеням (Т. 1: Основы учения о неделимых) / Пер., вступ. статья и коммент. С.Я. Лурье. М.; Л.: Гостехтеоретиздат, 1940. С. 5—80; С. 36—37.

44. Библер В.С. Галилей и логика мышления Нового времени... С. 506.

45. Галилей Г. Беседы... С. 240.

46. Там же. С. 242.

47. Гайденко П.П. Эволюция понятия науки (XVII—XVIII вв.)... С. 137.