«Слишком много ясности»

Почему, рассматривая полемику вокруг коперниканства, по крайней мере, те ее эпизоды и перипетии, которые оказались связанными со взглядами и поступками Галилея, я столько времени уделяю вещам, к космологической проблематике и к «делу Галилея» прямого отношения, казалось бы, не имеющим? На мой взгляд, в логическом аспекте — в аспекте логики доказательства — анализ «естественноускоренного движения» (свободного падения) и отстаивание коперниканских идей (особенно идеи подвижности Земли) имеют много общего. Приведу в подтверждение этой общности два фрагмента. Начну с одного эпизода третьего дня «Dialogo».

После того, как Сальвиати потратил уйму времени, расписывая «с какой легкостью и простотой годичное движение, если оно может быть приписано Земле, объясняет видимые несообразности, наблюдаемые в движении пяти планет <...>, вовсе устраняя их и сводя их к движениям равномерным и правильным», и растолковывая, почему движение солнечных пятен «побуждает человеческий разум признать это годовое обращение и отнести его к земному шару»¹, Симпличио, перед этим почти не выступавший с содержательными репликами, неожиданно бросает критическое замечание, на которое у Сальвиати не находится веских контраргументов. «Если по существу я не вполне усвоил рассуждения синьора Сальвиати, — признается Симпличио, — то, рассматривая их со стороны формы, я не нахожу, чтобы логика заставляла меня признать, будто из такого умозаключения с какой-либо необходимостью вытекают выводы в пользу гипотезы Коперника <...>. Ибо если верно, что при предположении такого вращения Солнца и такой орбиты Земли необходимо должны наблюдаться такие-то и такие-то особенности солнечных пятен, то отсюда еще не следует обратного, т. е. что из наблюдения таких особенностей пятен неизбежно надо сделать вывод о движении Земли <...> и о расположении Солнца в центре зодиака; ведь кто уверит меня, что подобные особенности не могут быть также видимы на Солнце, движущемся по эклиптике, жителями Земли, стоящей неподвижно в её центре?»²

И совершенно зеркальная (в логическом плане) ситуация складывается в «Discorsi». После того как Сальвиати привел доказательство закона свободного падения и вывел из него следствие (ПНЧ), Симпличио, до этого опять-таки больше молчавший, заявляет: «Теперь я в достаточной мере убежден, что явление (свободное падение. — И.Д.) должно происходить именно так (т. е. по (s ~ t²) закону. — И.Д.), если только принять указанное определение равномерно-ускоренного движения (т. е. V = at. — И.Д.). Но действительно ли таково ускорение, которым природа пользуется при движении тяжелых падающих тел, остается для меня сомнительным»³.

Суть замечаний Симпличио в обоих случаях фактически сводится к тому, что — процитирую Аристотеля — «хотя ложное всегда необходимо выводится через ложное, но истинное иногда может быть выведено через ложное» (Топ. VIII, 11, 162a)⁴, т. е. из истинности следствий не вытекает истинность посылок, и чтобы силлогизм стал обратимым, необходимо доказать истинность посылок или, по крайней мере, их единственность (безальтернативность), а поскольку аргументация Коперника и Галилея к этому последнему типу силлогизма не относится, все рассуждения Сальвиати не являются научными объяснениями, но только остроумными гипотезами. Какова же реакция Сальвиати-Галилея на эти возражения?

В первом случае (в «Dialogo») ответная реплика коперниканца свелась к тому, что объяснение движения солнечных пятен в рамках геоцентризма и «геостатизма» потребовало бы чрезвычайного усложнения теории — «Солнцу пришлось бы приписать четыре движения»⁵, из которых «два движения вокруг собственного центра, но около двух разных осей, одна из которых заканчивает свое обращение в один год, а другая меньше, чем в один месяц». «Такое допущение, — признается Сальвиати, — представляется моему разуму очень натянутым и даже невозможным»⁶. После чего разговор переводится на другую тему.

Во втором случае — в «Discorsi» — Галилей дает два ответа. Первый, с опережением сформулированный еще до того, как Симпличио высказал свои возражения, сводится к тому, что Природа «стремится применять во всяких своих приспособлениях самые простые и легкие средства», а потому не должны ли мы думать, что приращение скорости падающего камня «происходит в самой простой и ясной для всякого форме», ведь «нет превращения более простого, чем происходящего всегда равномерно»⁷. Т. е. Галилей, как и в предыдущей реплике, апеллирует к ясности, простоте и «экономичности» объяснений, т. е. скорее к критериям эстетическим, а не физическим или логическим. Вспомним в связи с этим восклицание Сагредо в адрес Сальвиати (т. е. фактически в адрес самого Галилея): «Слишком много ясности и слишком много простоты вносите вы в разъяснение темных вещей»⁸.

Второй ответ Сальвиати-Галилея на упрек Симпличио в недоказанности (V ~ t)-отношения сводится к описанию опытов с качением шаров по наклонной плоскости. Однако, как это признает и сам Сальвиати, опыты эти, повторенные «сотни раз», неизменно подтверждали правильность следствия, т. е. (s ~ t²)-зависимости, а не посылки, т. е. (V ~ t). После чего разговор опять-таки переводится на другую тему.

Да Симпличио особенно и не настаивал на прямом экспериментальном подтверждении именно (V ~ t)-отношения. Ему достаточно было нескольких опытов, «которые показали бы, что различные случаи падения тел совпадают со сделанными заключениями»⁹, т. е. подтвердили бы (s ~ t²)-зависимость и ПНЧ. Позиция перипатетика Симпличио понятна — в его глазах теория, изложенная в «De Motu locali» (как, кстати, и в «De Revolutionibus» Коперника) — не более, чем ex suppositione (или, как бы мы сегодня сказали, гипотетико-дедуктивная) конструкция, весьма характерная, по представлениям того времени, именно для так называемых смешанных (скажем, физико-математических) наук. Есть некая предпосылка ex-hypothesis, в данном случае — (V ~ t)-отношение, из неё получают следствия, которые затем проверяются опытным путем. И Сальвиати, замечу, против такого взгляда на теорию Академика не возражает: «Вы, — обращается он к Симпличио, — как подлинный ученый, предъявляете совершенно основательное требование; оно особенно уместно в отношении таких наук, в которых для объяснения законов природы применяются математические доказательства; таковы, например, перспектива, астрономия, механика, музыка и другие аналогичные науки; в них опыт, воспринимаемый чувствами, подтверждает принципы, являющиеся основою для всех дальнейших построений»¹⁰. При этом он полагал, что «если окажется, что свойства, которые будут доказаны ниже, справедливы и для движения естественно и ускоренно падающих тел, то мы сможем сказать, что данное нами определение (равномерно ускоренного движения: V ~ t. — И.Д.) охватывает и указанное движение тяжелых тел и что наше положение о нарастании ускорения в соответствии с нарастанием времени, т. е. продолжительностью движения, вполне справедливо»¹¹. Но если не единственными, то основными такими свойствами, подлежащими анализу на предмет их отношения к «естественно и ускоренно падающим телам», являются (s ~ t²)-отношение и ПНЧ.

Любопытные высказывания об этой гипотетико-дедуктивной процедуре можно встретить в переписке Галилея, например, в его письме Джованни Баттиста Балиани (G.B. Baliani) от 7 января 1639 г.: «Я ничего не предполагаю, кроме определения движения, о котором хочу толковать и чьи особенности (accidenti) хочу показать, подражая в этом Архимеду в его сочинении О спиральных линиях. В указанном сочинении Архимед, разъяснив, что он понимает под движением по спирали, слагающимся из двух равномерных, одного — прямолинейного, а другого — кругового, непосредственно переходит к демонстрации его свойств (passioni). Я заявляю, что хочу исследовать, каковы признаки (sintomi), присущие движению тела, начинающемуся с состояния покоя и продолжающемуся со все возрастающей одинаковым образом скоростью, а именно так, что приращения этой скорости происходят не скачками, но плавно (equabilmente), в соответствии с возрастанием времени. <...>. И не делая никаких других предположений, я перехожу к первой теореме, в которой доказываю, что отношение между путями, пройденными таким телом, является квадратом отношения между временами, и затем продолжаю доказывать большое число других особенностей. <...>.

Возвращаясь, однако, к моему трактату о движении, [скажу, что] я привожу доводы ex suppositione относительно движения, определенного указанным выше образом, так что даже если некоторые выводимые таким путем следствия не будут соответствовать всем особенностям естественного движения падающих тяжелых тел, то для меня это не будет иметь большого значения, ведь никто не упрекает доказательства Архимеда за то, что в Природе нет тел, движущихся по спирали. Но при этом <...> мне повезло (avventurati), поскольку движение тяжелых тел и их свойства в точности соответствуют свойствам, продемонстрированным мною, исходя из движения, мною определенного»¹².

И еще резче о том же — в письме Р. Каркави (P. Carcavy) от 5 июня 1637 г.: «если опыт покажет, что такие свойства [ускоренного движения] действительно обнаружатся в движении тяжелых тел, свободно падающих, то мы можем, не боясь ошибки, утверждать, что это и есть то самое движение, которое я определил и предположил; но даже если этого не произойдет, мои доказательства, основанные на моем допущении, ничего не потеряют в своей силе и убедительности»¹³.

Рис. 29. Диаграмма, представляющая соотношение величин V и t в случае монотонного возрастания V

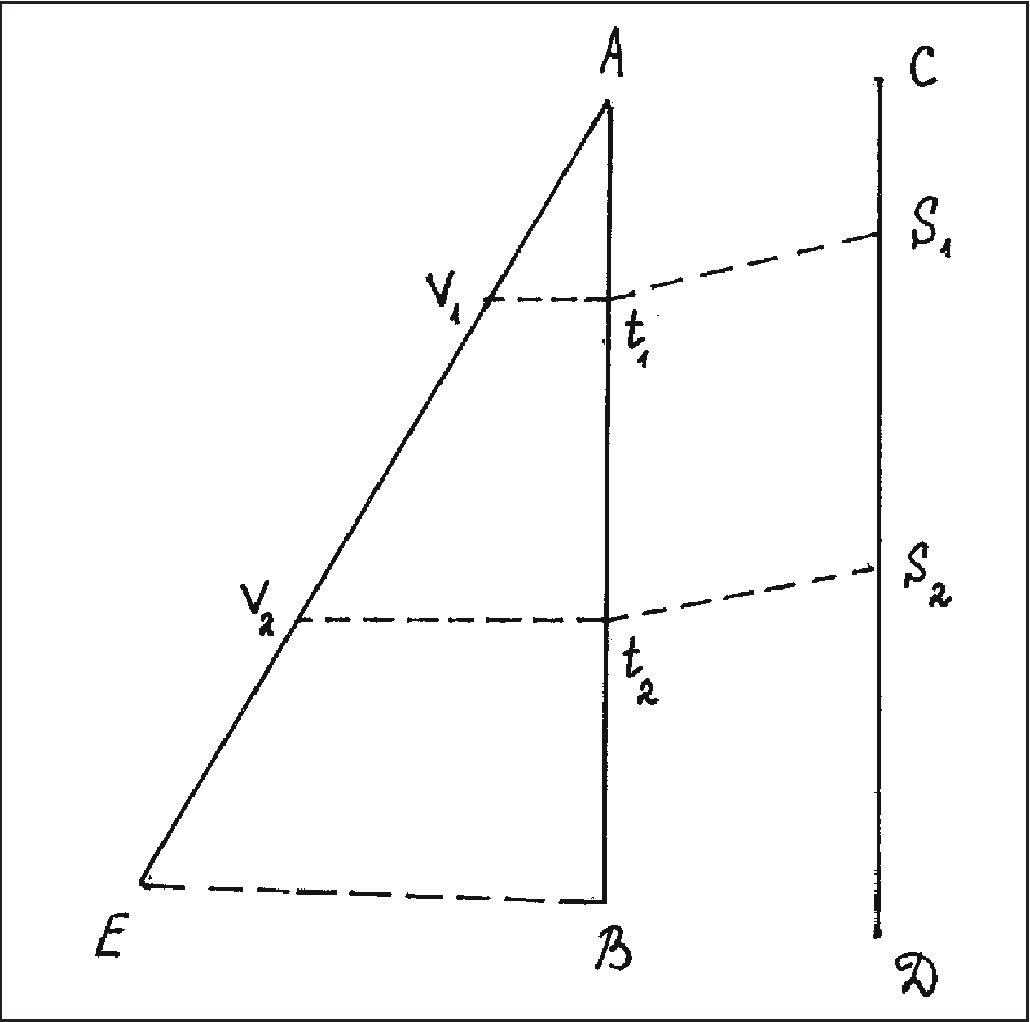
Так можно ли сказать, что выводы Галилея страдают fallacia consequentis? На первый взгляд — да, можно. Однако, если вдуматься, то ситуация не столь проста и однозначна.

Действительно, что давало Галилею основание утверждать, будто подтверждение следствия (s ~ t²) ведет к выводу о справедливости посылки (V ~ t), из которой это следствие было получено? Прежде всего, на мой взгляд, идея актуальной бесконечности деления конечного континуума (т. е. актуальности ненаблюдаемого), поскольку, опираясь именно на эту идею, он мог говорить о взаимно-однозначном соответствии между элементами следующих бесконечных множеств (рис. 29):

MT_AB ↔ MV_AB и MT_AB ↔ M_AB

(причем эти соотношения эквивалентности справедливы независимо от того, является ли функция V(t) линейной или нет, важно только то, что «приращение <...> скорости происходит не скачками, но плавно (equabilmente) в соответствии с возрастанием времени», т. е. важно, что функция V(t) — непрерывная и монотонно возрастающая; поэтому то, что диаграмма на рис. 29, представляющая соотнесенность V и t, имеет вид прямоугольного треугольника, в данном контексте неважно, важна лишь, повторяю, монотонность возрастания V и наличие указанных выше и ниже взаимнооднозначных соответствий);

MVAE ↔ MAE

MT_AB ↔ MV_AE ↔ MS_CD

и, следовательно,

M_AE ↔ M_AB ↔ MA_CD

Тогда из Merton Rule (в трактовке Галилея) следует, что

s₂/s₁ = V₂/V₁·t₂/t₁,

а т. к.

s₂/s₁ = t₂²/t₁²,

то

V₂/V₁·t₂/t₁ = t₂²/t₁²,

и

V₂/V₁ = t₂/t₁

т. e. V ~ t.

Всё это замечательно¹⁴, но... Оба вышеприведенных отношения путей s₂ и s₁ были получены исходя из допущения линейности функции V(t). И если по поводу второго отношения (s₂/s₁ = t₂²/t₁²) можно сказать, что его истинность была установлена экспериментально и потому не зависит от (V ~ t)-допущения, то первое (Merton Rule) — неразрывно связано с этим допущением¹⁵. Т. е. вывод V ~ t из s ~ t² упирается в проблему преодоления circulus vitiosus. Галилей, как будет ясно из дальнейшего, осознавал эту трудность и, возможно, поэтому уклонился от обсуждения доказательств (V ~ t)-допущения, исходя из закона свободного падения, а вовсе не потому, что такое доказательство было для него, как выразился З. Бехлер, «mathematically trivial»¹⁶. Галилей ограничился лишь констатацией следующих положений: скорость при свободном падении возрастает непрерывно и монотонно¹⁷; она зависит от времени, а не от пройденного пути.

Возможно, правы П. Дамеров и Г. Фрейденталь, отметившие, что в данном случае обоснование прямой пропорциональности между V и t, понимаемое «как некое отдельное, особое доказательство (a particular proof) типа доказательства закона свободного падения, по-видимому, не нужно и даже невозможно»¹⁸.

Примечания

1. Галилей Г. Диалог... С. 439.

2. Галилей Г. Диалог... С. 446—447.

3. Галилей Г. Беседы... С. 252.

4. См. также: Аристотель. Первая аналитика. II, 2, 53в; 4, 57а.

5. Галилей Г. Диалог... С. 447 (маргиналия).

6. Галилей Г. Диалог... С. 449.

7. Галилей Г. Беседы... С. 239.

8. Там же. С. 245. Не следует забывать, что и «Dialogo», и «Discorsi» несут на себе среди прочего также явные отпечатки того, что сейчас называют саморекламой, и причина тому не только личные качества их автора.

9. Там же. С. 253.

10. Галилей Г. Беседы... С. 253.

11. Там же. С. 241.

12. Galilei G. Le Opere. Vol. XVIII. P. 11—12. Перевод В.П. Зубова (Григорьян А.Т., Зубов В.П. Очерки... С. 114).

13. Galilei G. Le Opere. XVII. P. 90.

14. З. Бехлер предложил более простой, я бы даже сказал, наивный аргумент: т. к. «площадь под кривой V(t) пропорциональна s(t)», то, «поскольку s ~ t², A (площадь четырехугольника. — И.Д.) ~ t², а т. к. абсцисса есть t, то ордината V должна быть V(t) ~ t» (Bechler Z. Newton's Physics... P. 121). Фактически аргумент Бехлера совпадает с приведенным мною в основном тексте. Действительно, т. к. A ~ s(t) ~ t² и s(t) ~Vt, то V ~ t.

15. Кстати, по аналогичной причине «не проходит» и приведенный в прим. 596 аргумент З. Бехлера.

16. Ibid. P. 121.

17. Если скорость изменялась бы скачками, т. е. график V = V(t) имел бы вид ступенчатой функции, то тогда, как это было известно, по-видимому, еще до Галилея, отношение пройденных путей определялось бы не ПНЧ, но отношением чисел натурального ряда (1: 2: 3: 4: ... и т. д.).

18. Damerow P., Freudenthal G., McLaughlin P., Renn J. Exploring the Limits... P. 50. Я полагаю, читатель помнит о том, что Галилей не мог воспользоваться в своих рассуждениях методами дифференциального и интегрального исчислений, разработанными позднее.