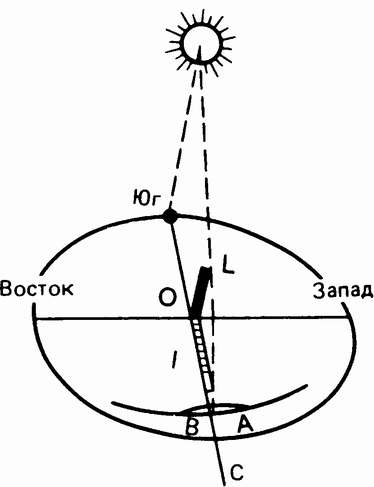
Солнце отсчитывает время днем

Египтяне еще в начале 2-го тысячелетия до н.э. разделили небесный свод на созвездия. Вначале было всего 23 созвездия, которые весьма существенно отличались от современных. Зодиакальных созвездий не было, а Большую Медведицу называли Быком, связывая ее, скорее всего, со священным животным Апис — символом плодородия. Считалось, что Бык четырьмя вожжами соединен с небесным полюсом и в таком состоянии поддерживается божествами, олицетворяющими четыре стороны света. Вместо Малой Медведицы было созвездие Гиппопотама, часть созвездия Дракона называлась Крокодилом и т. д.

Деление неба на созвездия помогало определению времени ночью. Днем же время отсчитывалось по солнечным часам, самые древние из которых датируются XV в до н.э. Стрелкой служила тень, отбрасываемая палочкой, расположенной горизонтально по направлению север — юг. Под ней была соответствующая горизонтальная шкала часов. Позднее, в начале 1-го тысячелетия до н.э., в употребление вошли часы другой конструкции, в которых горизонтальная шкала была заменена наклонной плоскостью. В период Нового царства были созданы даже переносные часы такой конструкции, которые носили на шее. Найден их образец времен XIX династии, а также письменная инструкция по применению.

Древние египтяне использовали также солнечные часы другой конструкции, в которых время отсчитывалось по длине тени вертикальной палочки на циферблате, расположенном под углом к горизонту. Его поверхность была ступенчатой, и при восходе Солнца тень палочки попадала на самую крайнюю западную ступень. В течение дня тень скользила по ступеням, которые обеспечивали отсчет одинаковых промежутков времени. После полудня тень переходила на восточные ступени, и до захода Солнца ситуация повторялась в обратном порядке.

Здесь интересно заметить, что на территории Болгарии в округе Силистра были найдены солнечные часы, сделанные из камня в III в. н.э. На часах изображены боги Исида и Осирис — Серапис, а также играющий на лире Орфей, окруженный птицами и другими животными, зачарованными музыкой.

По-видимому, обелиски, дошедшие до наших времен от древних египтян, служили не только для поклонения богу Солнца, но также для приблизительного ориентирования во времени днем, т.е. как часы. Простой астрономический прибор такого типа, называемый гномоном, помимо слежения за временем дает возможность проводить некоторые простые измерения.

Представим себе прямую палку, поставленную вертикально. В солнечный день за час-два до полудня отметим на горизонтальной плоскости край тени (буква А на рис. 25). Привяжем к основанию палки О веревку и проведем с ее помощью дугу окружности радиусом OA. Пройдя точку А, тень палки начнет сокращаться, а после полудня — снова удлиняться. Достигнув снова длины OA, тень коснется точки В на окружности. Разделим расстояние BA на две равные части и проведем луч ОС. Какие выводы мы можем сделать?

Рис. 25. Гномон — один из древнейших астрономических приборов.

Во-первых, прямая ОС есть полуденная линия. Она пересекает горизонт в точках юга и севера, т. е. там же, где проходит главный меридиан. Другими словами, такое простое наблюдение позволяет легко узнать направления сторон света. Во-вторых, момент, когда тень совпадает с линией ОС, есть середина дня по местному времени (12 ч). Так мы получаем точку отсчета времени днем. Более того, мы можем сделать одинаковую по расстоянию разметку на запад и на восток от ОС и отсчитывать мелкие интервалы времени до и после полудня. Однако этим возможности гномона не исчерпываются. В-третьих, с ним можно определить географическую широту φ места наблюдений и, в-четвертых, угол ε между эклиптикой и экватором. Посмотрим, как это делается.

В главе, посвященной Стоунхенджу, было показано, что в момент кульминации астрономического объекта (т. е. прохождения через меридиан) его высота над горизонтом равна h = 90° - φ + <5. Там же говорилось, что Солнце достигает максимальной высоты в день летнего солнцестояния, когда его склонение равно ε ок. +23,5°, и минимальной — в день зимнего солнцестояния при склонении — ε ок. -23,5°. Измерим в эти дни тень гномона и вычислим затем максимальную и минимальную полуденную высоту Солнца в году h_мин и h_макс (о том, как это сделать, — чуть ниже). Тогда получим

h_макс = 90° — φ + ε h_мин = 90° — φ — ε.

Сложим эти два равенства:

hмакс + hмин = 180° — 2φ,

откуда

φ = 90° — (h_макс + h_мин)/2.

А теперь отнимем h_мин от h_макс. Получим

h_макс — h_мин = 2ε,

откуда

ε = (h_макс + h_мин)/2.

Таким образом, в одном случае мы получаем возможность вычислить географическую широту места наблюдений, а в другом — наклон эклиптики к экватору. По-видимому, именно эти зависимости использовали в древности при наблюдениях с гномоном китайцы, Гиппарх, индейцы майя и представители других народов в разных местах для вычисления ε. Все это мы еще будем рассматривать ниже.

А пока выясним, как по измеренной длине тени можно установить высоту Солнца над горизонтом. Если высота гномона равна L, а длина тени l, то из элементарной математики получаем соотношение L/l = tg h. Отсюда и определяется высота h.