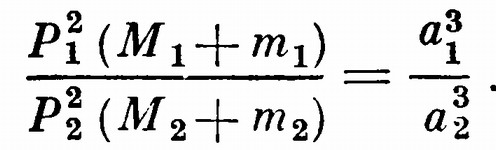Законы Кеплера

Кеплер открыл три закона движения планет, которые это движение вполне определяют. Он указал в первом законе, что планеты обегают Солнце по эллипсам, у которых один из двух фокусов непременно совпадает с Солнцем¹. Во втором законе Кеплер говорит, что при движении планеты отрезок прямой, соединяющей планету с Солнцем, в единицу времени всегда описывает одну и ту же площадь. Третьим законом Кеплер установил, что квадраты времен обращения планет P пропорциональны кубам их средних расстояний от Солнца a, т. е.

где значки 1 и 2 относятся к двум любым планетам.

Все эти три закона — следствие всемирного тяготения, как показал Ньютон. Они справедливы и для движения спутников вокруг своих планет и для движения любого тела под действием притяжения к другому. Только в некоторых случаях движение может происходить не по эллипсам, а по другим, уже незамкнутым кривым — параболе или гиперболе (см. рис. 29). Они также имеют фокусы, и главное тело всегда будет в фокусе такой орбиты. Если тело движется не по замкнутой орбите, то тогда, конечно, о периоде обращения нельзя говорить и третий закон Кеплера для таких орбит не имеет смысла. В случае же движения по эллипсу, как показал Ньютон, третий закон правильнее писать так:

Его можно применить к любым двум массам M₁ и M₂, из которых первая имеет спутник с массой m₁ обращающийся вокруг нее с периодом P₁ на среднем расстоянии a₁, а вторая масса M₂ имеет свой спутник массы m₂ с периодом обращения P₂ на среднем расстоянии a₂. По этой формуле можно сравнить, например, движение Луны около Земли с движением Земли около Солнца или с движением спутника Нептуна около своей планеты. Если массы спутников ничтожно малы в сравнении с массами своих центральных тел, то ими в формуле можно пренебречь. Тогда, применяя ее, например, к двум планетам — спутникам Солнца, мы можем сократить массу Солнца в числителе и в знаменателе, и формула получит тот вид, в каком ее и дал сам Кеплер. Его формула — приближенная, но она достаточно точна для планет Солнечной системы, так как масса их всех, вместе взятых, в 750 раз меньше массы Солнца.

Уточнение же, приданное ей Ньютоном, необычайно важно тем, что позволяет определять массы небесных тел, введенные им в формулу третьего закона Кеплера.

Притяжение планет друг другом невелико по сравнению с их притяжением к Солнцу, но оно вызывает отклонения в движении, несколько меняет вид и положение орбит. Эти отклонения называются возмущениями. На много лет вперед величину возмущений можно вычислить, зная массы взаимодействующих тел и их орбиты в некоторый момент.

Движение планеты легко себе представить, если знать форму и положение ее орбиты в пространстве, а также положение планеты на орбите в какой-нибудь момент. Величин, характеризующих эти данные, шесть, они называются элементами орбиты. Но для нас достаточно будет познакомиться только с четырьмя из этих элементов.

Примечания

1. Как известно, эллипсом называется кривая, сумма расстояний до любой точки которой от двух заданных точек (их называют фокусами эллипса) одна и та же.