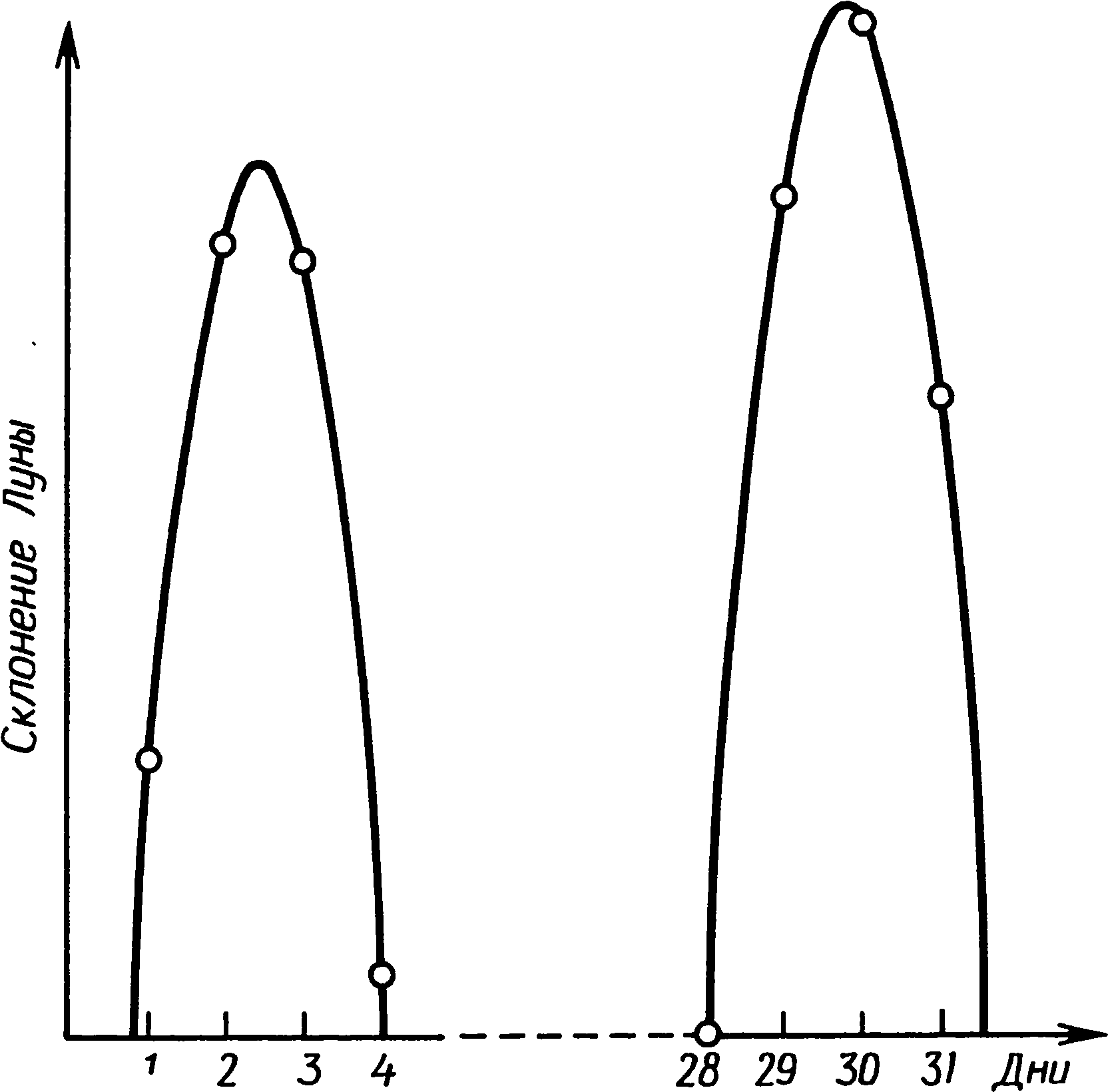
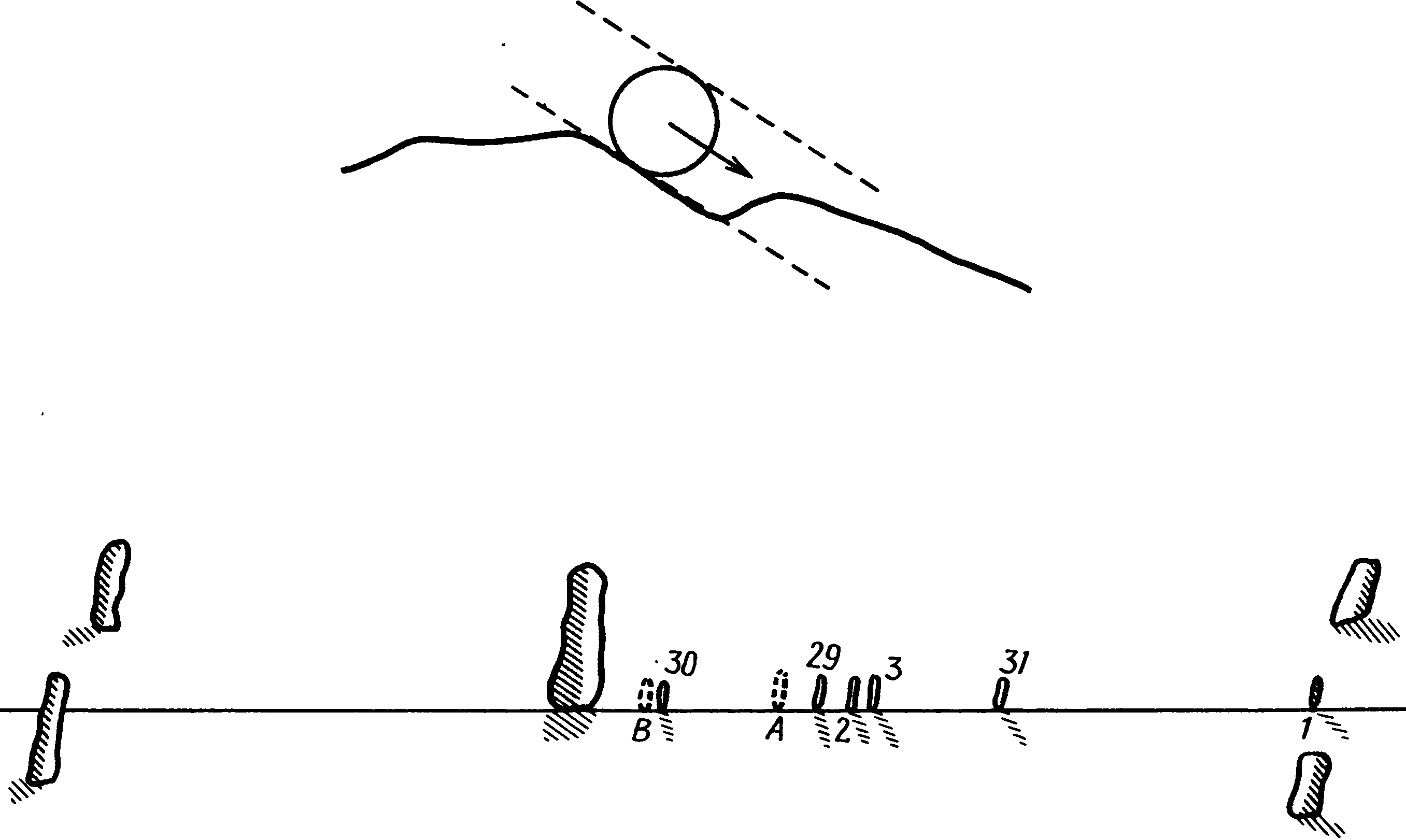
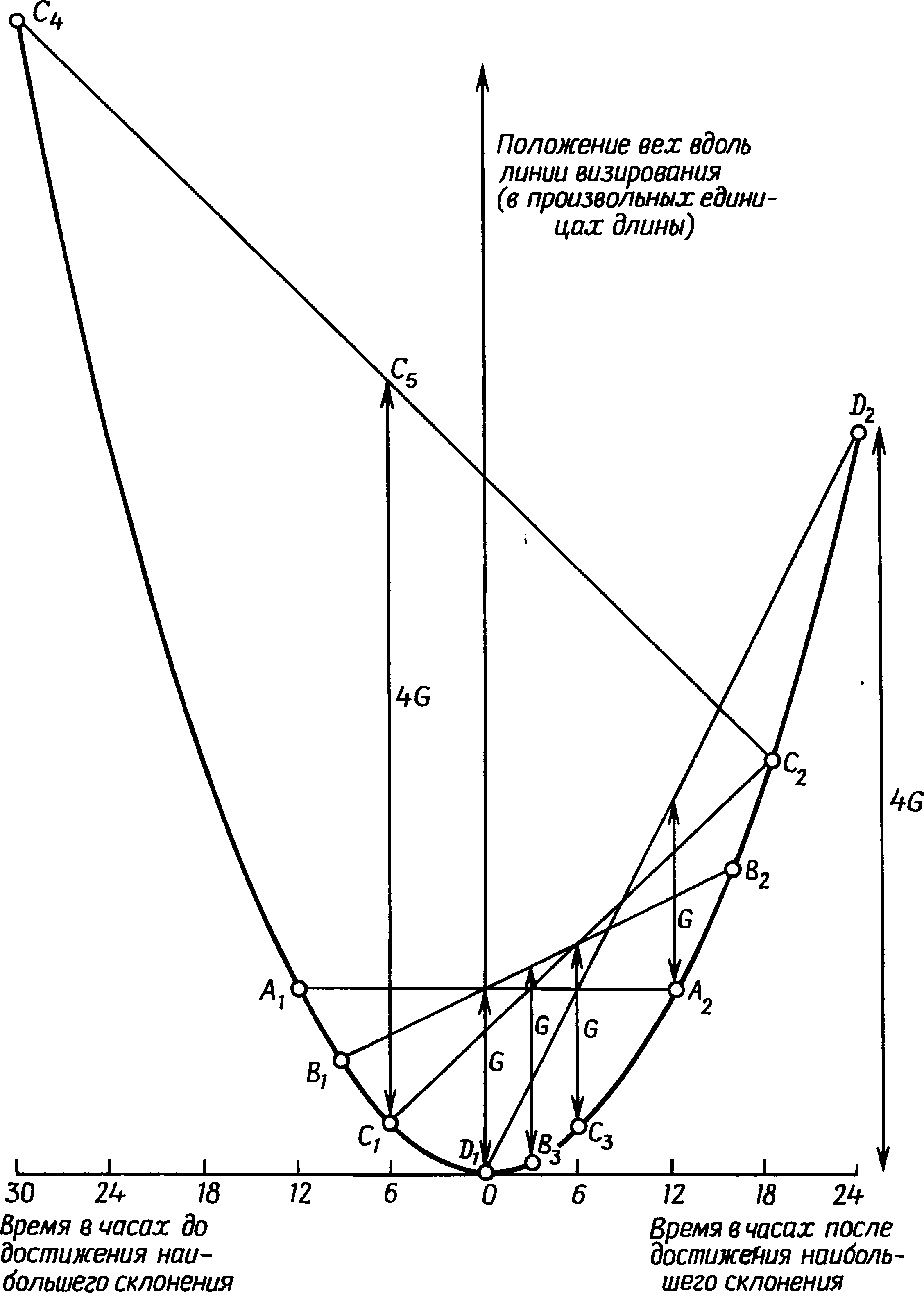
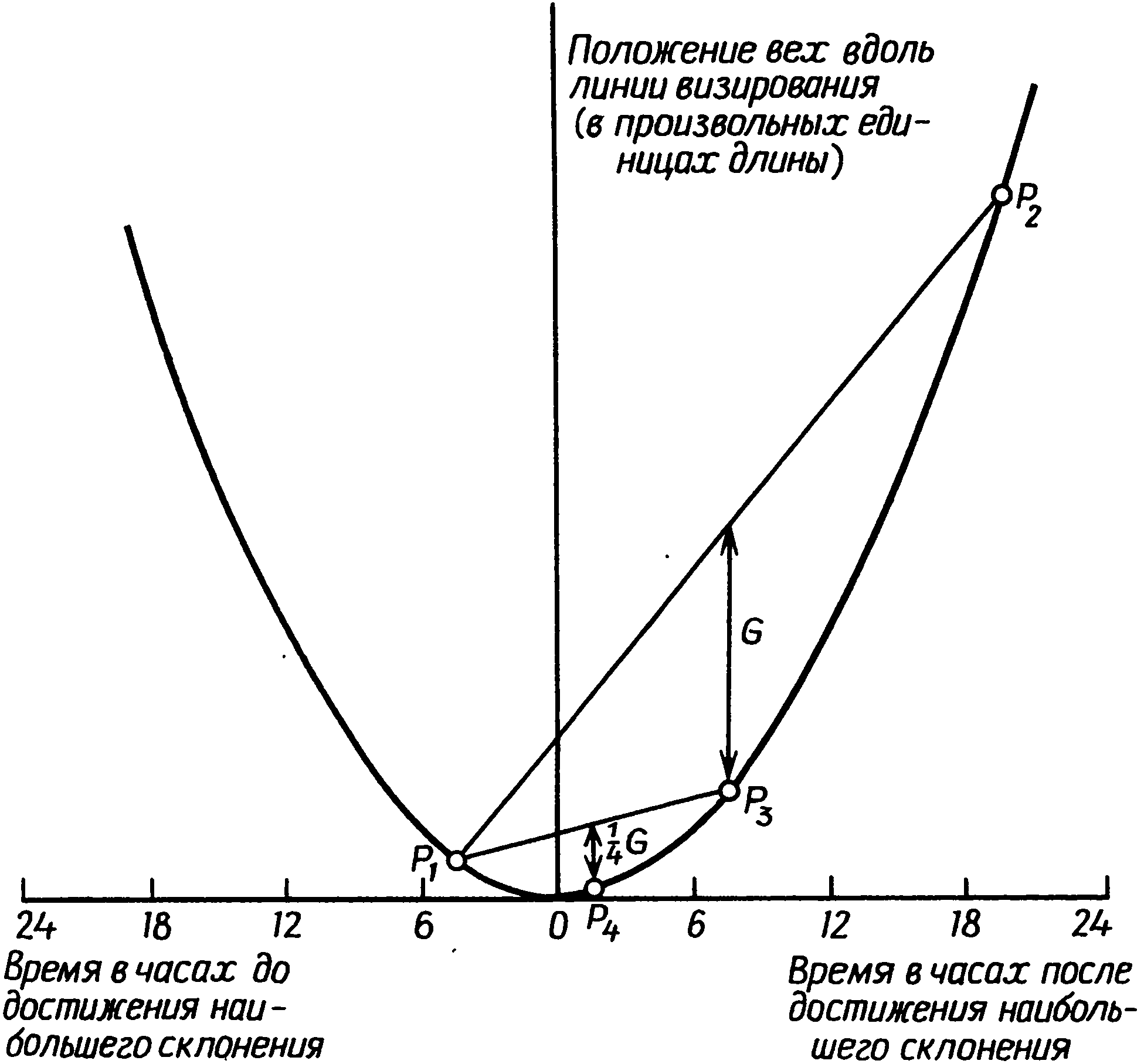
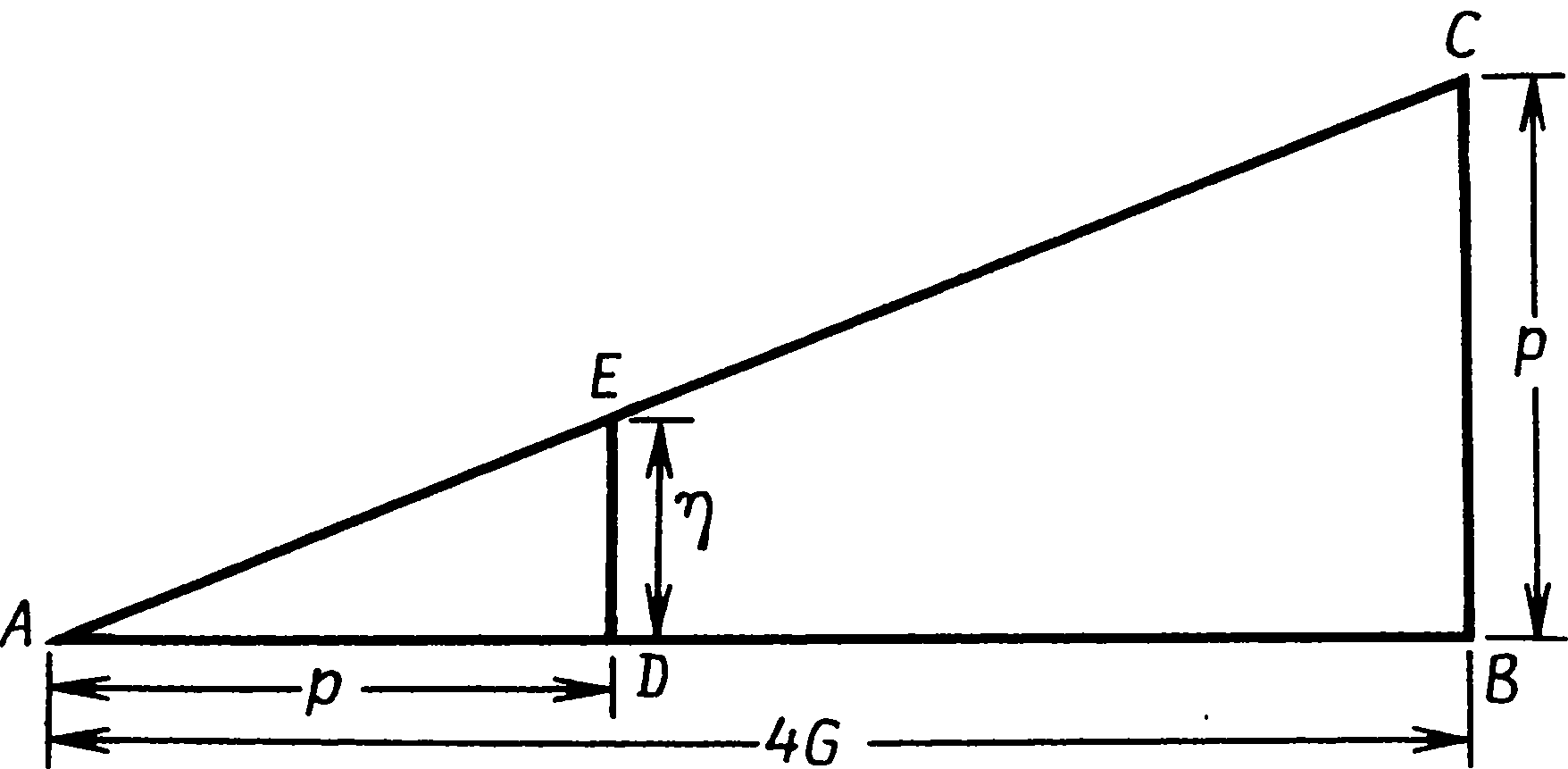
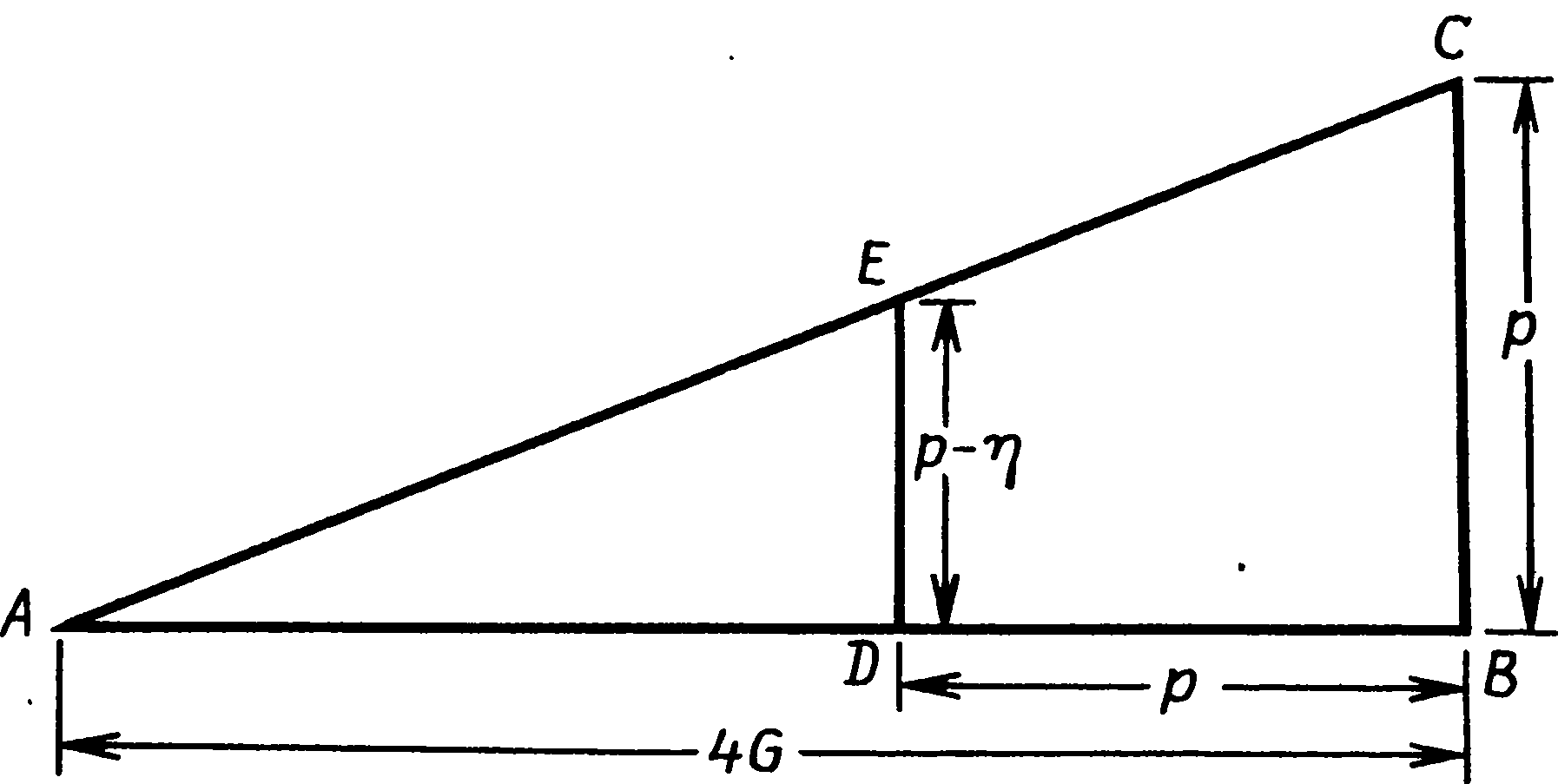
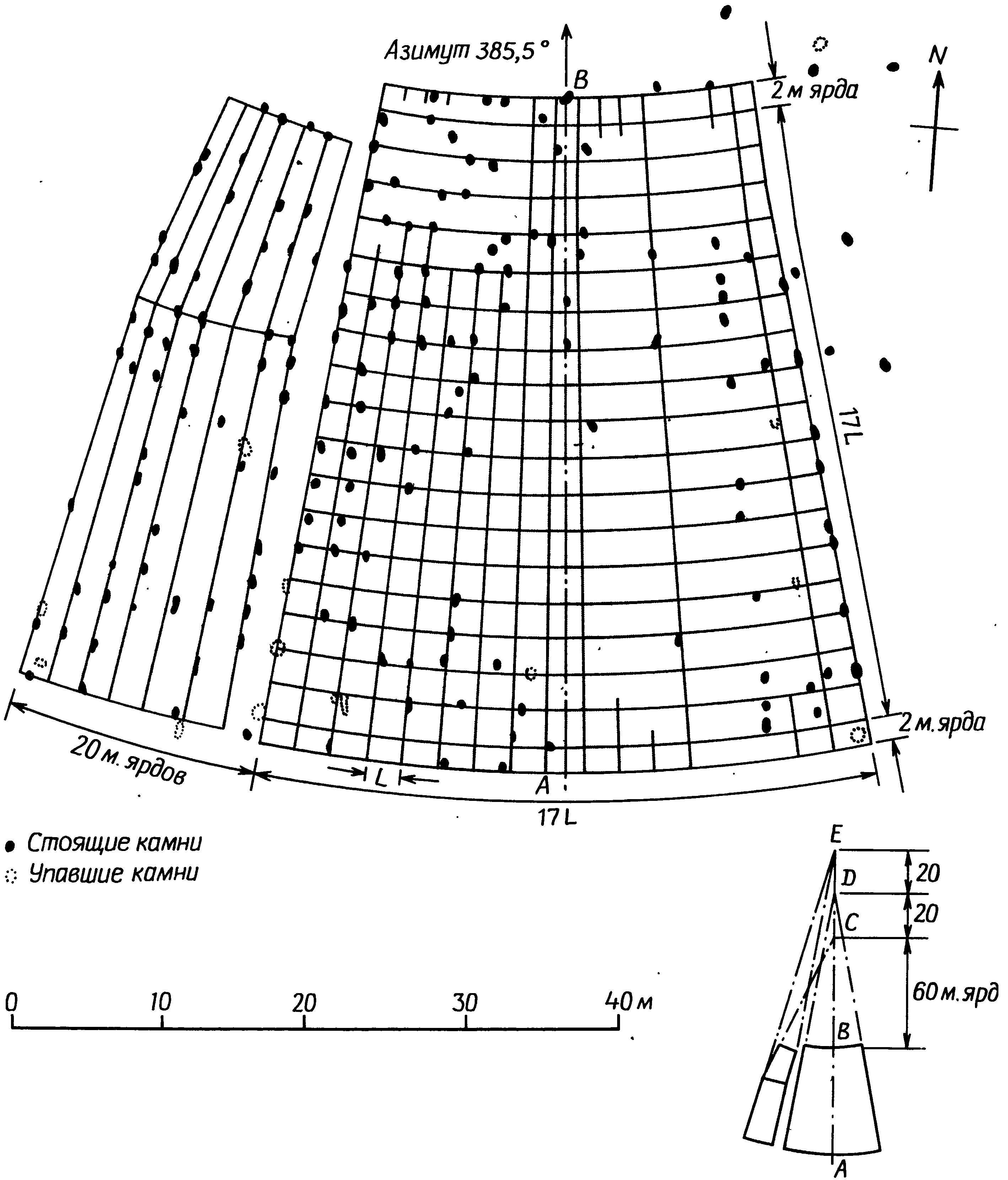
7. Счетные устройства бронзового века

Чтобы описать процесс вычисления максимального склонения Луны по измерениям, произведенным не в максимуме, ученые, занимающиеся лунными обсерваториями, употребляют слово «экстраполяция». Применение этого термина вполне оправданно, так как на языке современной математики экстраполировать — значит оценивать величину, лежащую вне ряда уже известных величин. Обычным примером экстраполяции может послужить прогнозирование будущего экономического состояния той или иной отрасли промышленности по регулярно поступающим цифрам ее торгового оборота.

Однако в отличие от экономических прогнозов, которые всегда чреваты ошибками, положение Луны на будущее время предсказывается теперь совершенно достоверно, так как известны все факторы, определяющие ее движение. Каждый месяц склонение Луны изменяется по кривой, которая называется синусоидой. Эта периодически повторяющаяся кривая, в частности, описывает картину движения маятника, колебаний камертона, изменения напряжения в цепи переменного электрического тока и еще многого другого. Для решения нашей проблемы экстраполяции результатов наблюдений, произведенных в непосредственной близости от максимального склонения, нам нужен только небольшой отрезок синусоиды вблизи ее вершины, а его можно представить с помощью более простой математической кривой — параболы. Парабола — это, например, траектория брошенного мяча, а также граница освещенного участка, когда конус света от электрического фонарика падает на стену не под прямым углом. Ниже в этой главе мы будем считать, что склонение Луны вблизи его максимума изменяется по параболе.

В раннем бронзовом веке астрономы не знали математических приемов, которые помогали бы им проводить экстраполяцию. Но они начинали не на совсем уж пустом месте. Как мы узнали, рассматривая геометрию каменных кругов и колец, они умели точно измерять расстояния, считать до довольно больших чисел, строить прямые углы и вычерчивать очень сложные фигуры. В поисках решения они, несомненно, опирались на уже имевшиеся у них знания, и учитывая это, мы, возможно, сумеем понять, как они справились с проблемой экстраполяции. Но в одном мы можем быть твердо уверены: современными математическими методами они не пользовались.

Рис. 7.1. Склонение Луны в двух последовательных максимумах

Какой же представлялась эта проблема в раннем бронзовом веке? Вообразим себе обсерваторию вроде Темпл-Вуда, где более или менее перпендикулярно к направлению на выемку (высокой точности тут не требуется) проложена линия, вдоль которой мегалитические астрономы, вероятно, становились, чтобы наблюдать заходы Луны. Типичная картина изменения склонения Луны на протяжении двух следующих друг за другом месяцев изображена на рис. 7.1. Каждый месяц оно достигает наибольшего значения, а затем уменьшается. Кружки на кривой схематически показывают, каким могло быть склонение Луны в моменты ее захода. В первом максимуме заходы наблюдались с первого по четвертый день, причем на второй и третий дни склонение Луны оказалось почти одинаковым. Наблюдатели вбили маркировочные колья, как это показано на рис. 7.2, отмечая, где они стояли, чтобы видеть, как нижний край Луны спускается по склону выемки. Колья, установленные на второй и третий день, расположены очень близко друг к другу; где-то слева от них находится то неизвестное положение (A), которое должны были бы занимать наблюдатели, если бы Луна заходила при максимальном месячном склонении.

Затем в течение 25 ночей наблюдения не производились, так как Луна заходила слишком далеко к югу и использовать это направление было нельзя. Предположим, что при следующем максимуме маркировочные колья были вбиты на 29, 30 и 31-й дни. В этом случае оба левых кола расположены относительно далеко друг от друга, а неизвестное положение кола, который отметил бы максимальное склонение, находится только чуть левее левого кола этой пары, в точке B. Задача экстраполяции, естественно, сводится к тому, чтобы, опираясь на положение установленных кольев, найти точки A и B.

Рис. 7.2. Как должны располагаться вехи при двух максимальных склонениях Луны, показанных на рис. 7.1

Серия регулярных наблюдений достаточно быстро позволила бы обнаружить некоторые закономерности. Из наблюдений, произведенных в три ближайших к максимуму дня, можно было бы вывести простое правило, связывающее положения кольев: расстояние от крайнего левого кола до средней точки между остальными двумя кольями каждый месяц оказывается совершенно одинаковым. Без сомнения, наблюдатели сочли бы его особым, характерным, расстоянием для данного направления, которое было бы очень полезно — если бы пасмурная погода помешала провести наблюдения в день, ближайший к максимальному месячному склонению, то с помощью этого правила можно было бы найти положение нужного кола. Кроме того, наблюдатели могли бы заметить, что расстояние между двумя левыми кольями никогда не бывает больше расстояния, характерного для данного направления, хотя, конечно, чаще оно оказывается меньше. Сравнивая результаты, полученные на одной обсерватории, с результатами другой, они могли обнаружить, что характерное расстояние зависит от удаления выемки на горизонте. Чем ближе выемка, тем такое расстояние меньше.

Понятие характерного расстояния, присущего каждой отдельной лунной обсерватории, должно было стать известно тем, кто ею пользовался, на очень раннем этапе. Производя одновременно два наблюдения захода Луны с использованием верхнего и нижнего ее края, они обнаружили бы, что расстояние, разделяющее поставленные при этом два кола, хотя и не одинаковое каждый раз, изменялось бы в очень узких пределах. Среднее расстояние между ними было больше, если выемка находилась на отдаленном горизонте. Собственно говоря, для каждой линии визирования имеется свой наземный эквивалент лунного диаметра. Сопоставив его с максимальным разносом маркировочных кольев за две следующие друг за другом ночи, они открыли бы, что наземный эквивалент лунного диаметра составляет чуть больше половины максимального расстояния между кольями для направления, связанного с «высокой» Луной, и примерно равен ему при «низкой» Луне. Это правило применимо ко всем лунным обсерваториям.

Дальнейшую качественную информацию дало бы им изучение положения кольев, отмечающих максимальное найденное за месяц склонение, то есть положение крайних левых кольев за каждый месяц, поставленных в лунной обсерватории вроде Темпл-Вуда. Колья, указывающие месячный максимум, постепенно, но неравномерно сдвигались бы влево, а затем начинали бы отступать вправо по мере того, как «высокая» Луна начинает свой путь к «низкому» положению. При этом довольно часто обнаруживался бы выпадающий из серии кол, который оказался правее ожидаемого положения. Сообразительный наблюдатель в конце концов понял бы, что крайний левый кол данного месяца оказывается словно бы в наилучшем положении, когда он отделен от ближайшего соседа некоторым расстоянием. И наоборот, если соседний кол оказывался слишком близко, то левый кол не вписывался в месячный ряд. Отсюда лишь небольшой шаг до вывода, что правильное положение для кола, показывающего месячный максимум, слева от крайнего левого кола, поставленного в результате прямых наблюдений, и что для получения этого положения надо отложить влево от последнего кола какое-то расстояние — небольшое, если поставленные в предыдущие ночи колья находятся далеко друг от друга, и большее, если они стоят почти рядом.

Мы можем графически представить весь этот процесс на рис. 7.3. Кривая изображает изменение склонения Луны, или, что то же, положение на Земле, которое должен занять наблюдатель, чтобы увидеть, как Луна заходит в выемку. Вместо того чтобы нанести проекцию всех точек на линию наблюдения, как, скорее всего, делалось с кольями в обсерваториях, мы оставим их на кривой, показывающей зависимость их положения от времени (в часах) до и после максимального склонения. Эта кривая представляет собой параболу, и ее вершина соответствует максимальному склонению. В своих объяснениях мы допустим незначительную неточность, приняв, что заходы Луны всегда разделены 24 часами.

Положение кольев, отмечающих заходы Луны за 12 часов до и через 12 часов после максимального склонения, представлено точками A₁ и A₂. Чтобы отметить максимальное склонение, надо поставить кол в точке D₁, в вершине параболы. Он должен находиться на расстоянии G от средней точки между кольями A₁ и A₂.

Рис. 7.3. Зависимость расположения вех от времени захода Луны в ночь наибольшего склонения

Если Луна заходила за 9 часов до и через 15 часов после максимального склонения, то колья окажутся в точках B₁ и B₂. Вбив кол на расстоянии G от середины расстояния между ними, мы получим точку B₃, которая находится ближе к вершине, чем B₁ и B₂. Проделав то же с другой парой точек, C₁ и C₂, мы увидим, что расстояние G, отложенное от середины между парой кольев, всегда дает на параболе третью точку. Другими словами, если наблюдатели нашли среднюю точку между двумя кольями, поставленными вблизи максимума, а затем отложили влево от нее расстояние G и вбили там еще один кол, они прошли хотя бы часть пути — но не обязательно весь путь — к правильному положению кола D.

Особенно интересно посмотреть, что будет, когда Луна заходит точно в момент максимального склонения. Тогда в следующий раз она зайдет через 24 часа, и колья окажутся в точках D₁ и D₂. В этом случае оба кола максимально удалены друг от друга. Отложив расстояние G от середины расстояния между кольями D₁ и D₂, получим точку A₂ , которая отстоит от нужной точки опять-таки на расстояние G. Из чертежа ясно, что расстояние между D₁ и D₂ равно 4G.

Мы можем ввести характерное расстояние данной линии визирования, отложив еще одну точку, например C₄, которая представляет результат наблюдения, сделанного на 24 часа раньше, чем то, которое дало точку C₁. Расстояние от середины между точками C₂ и C₄ до C₁ (т.е. от C₅ до C₁) уже было определено как характерное расстояние для данного направления, и из рис. 7.3 видно, что оно равно также 4G. Тот же результат был бы получен, если бы мы использовали точки, найденные при наблюдении за 24 часа до A₁, B₁ или D₁. Следовательно, характерное расстояние для данного направления равно 4G, и, кроме того, оно же является максимальным между кольями, вбитыми в две следующие друг за другом ночи около времени максимального склонения.

Подведем итоги.

а. У каждой обсерватории есть свое характерное расстояние 4G для каждой линии визирования. Расстояние это легко определяется по наблюдениям трех последовательных заходов Луны и представляет собой, кроме того, максимальное возможное расстояние, разделяющее два маркировочных кола, установленных при наблюдении двух лунных заходов, ближайших по времени к максимальному склонению.

б. Пара кольев не дает максимального склонения для данного месяца; должен быть установлен третий кол левее левого кола пары на расстоянии, которое зависит от расстояния, разделяющего колья пары.

в. Когда оба кола пары оказываются в одной точке, правильное положение третьего кола находится путем откладывания влево расстояния, равного одной четверти характерного расстояния, т.е. G.

г. Когда два кола не оказываются в одной точке, обкладывания влево от средней точки пары расстояния G недостаточно. Чем больше расстояние, разделяющее пару, тем большую ошибку дает такой метод экстраполяции. Когда расстояние между кольями равно 4G, для нахождения верного положения необходимо отложить от середины 2G.

д. Все вышесказанное прямо применимо к заходам Луны. То же самое наблюдается при восходах Луны, но все перемещения наблюдателя будут направлены в противоположную сторону. Для экстраполяции положения максимального склонения ему придется идти вправо.

Современные научные знания дают нам возможность вычислять величину 4G по астрономическим постоянным и по геометрическим характеристикам места наблюдения. Для «высокой» Луны уменьшение склонения от максимального составляет за первые 24 часа 0,91°, а для «низкой» — 0,55°. (Некоторые авторы дают уменьшение за 12 часов, и тогда оно вчетверо меньше.) Изменение азимута, соответствующее такому уменьшению склонения, можно найти с помощью уравнения (1) в гл. 4, и, чтобы перевести эту величину в реальное перемещение наблюдателя, надо умножить разность азимутов (в радианах) на расстояние от выемки до места наблюдений. Когда предполагаемая линия кольев перпендикулярна линии визирования, мы сразу получим верный результат; но если линия кольев и направление визирования расположены не под прямым углом друг к другу, как, например, в Темпл-Вуде, то необходимо разделить полученный результат на синус угла между ними. Если на площадке, выбранной для наблюдений, есть неровности, то необходимо внести еще и другие поправки.

К несчастью, не существует никаких письменных памятников раннего бронзового века, из которых мы могли бы узнать, как люди, пользовавшиеся обсерваториями, брались за решение проблемы экстраполяции. Мы видим в археологических памятниках того периода только конечные результаты их трудов, которые и должны изучать и анализировать в поисках ключей к отгадке. Рассчитывая характерное расстояние для разных памятников и сравнивая его с сохранившимися их остатками, археологи склоняются к заключению, что люди раннего бронзового века открыли понятие характерного расстояния, поскольку для некоторых памятников оно запечатлено в расстояниях между стоячими камнями или в каких-либо других сооружениях того же периода. В Темпл-Вуде имеется два разных направления, и, поскольку их дальние визиры находятся на разных расстояниях (2,0 и 6,3 км), для 4G должно быть также два значения. По расчетам они составляют соответственно 83 и 308 м. Когда профессор Том и его сотрудники впервые исследовали этот памятник в 1939 г., они заметили небольшой кернообразный бугор в точке Y (рис. 6.9.), в 81 м от центрального менгира. Это очень близко к правильному значению 4G для направления на ближайшую из двух выемок, и профессор Том предположил, что бугор и должен был служить постоянной засечкой этого важного расстояния.

Во втором случае величина 4G запечатлена гораздо более эффектным способом. Внимательно изучая план Темпл-Вуда, мы обнаруживаем, что расстояние от самого большого менгира до центра каменного кольца составляет 300 м, а это менее чем на 3% отличается от значения 4G для направления на холм Белланох. Мы уже упоминали, что каменное кольцо и керн лежат на одной прямой с ближней выемкой, а потому, видимо, были сооружены позже лунной обсерватории. Если мы примем, что в них сознательно запечатлены характерные расстояния, то из этого следует, что кольцо и керн были сооружены в то время, когда обсерваторией постоянно пользовались, и, вероятно, вскоре после того, как была закончена она сама. Темпл-Вуд представляет собой редкий пример прямой связи между группой стоячих камней и памятником другого типа, относящимся к раннему бронзовому веку.

Раз мы знаем, что те, кто пользовался лунной обсерваторией Темпл-Вуд, открыли характерное расстояние 4G и запечатлели его там, возникает естественный вопрос: как могли они употребить свое открытие для экстраполяции? Имеющиеся данные указывают, что их метод экстраполяции был вполне точным, поскольку камни, показывающие направления, установлены с точностью до 1/50°. Если данная обсерватория должна была предсказывать затмения путем определения максимума малых возмущений, ежемесячный максимум склонения Луны необходимо было определять с точностью именно такого порядка. При использовании ближней выемки 1/50° эквивалентна перемещению по земле менее чем на 2 м. При прямых наблюдениях, без экстраполяции, наибольшая ошибка могла бы достигнуть G, т.е. примерно 20 м — в десять раз больше, чем можно было бы допустить для эффективного использования обсерватории.

Дав на минуту волю воображению, попробуем восстановить тот логический путь, который могли бы пройти астрономы раннего бронзового века в процессе изучения результатов своих наблюдений. Начнем с предположения, что они уже открыли характерное расстояние, запечатлели его на земле и поняли связь между результатами наблюдений в три следующие друг за другом ночи во время, близкое к максимальному месячному склонению, т.е. знали, что положение маркировочного кола в среднюю из ночей можно найти, отложив характерное расстояние влево от средней точки между двумя другими кольями.

Рис. 7.4. Метод экстраполяции путем последовательного добавления G, G/4, G/16 и т.д.

Самый левый из трех кольев явно гораздо ближе к правильному положению месячного максимума, но он, несомненно, не находится в верной точке. Должно существовать невидимое (магическое?) положение кола дальше влево, а раз самое левое из трех положений можно найти даже в облачную ночь по остальным двум положениям, то, может быть, если повторить тот же ритуал, это позволит определить положение невидимого кола? Почему бы не отложить еще какое-то расстояние влево от середины между двумя крайними кольями? Но каково это неизвестное расстояние? Как они могли открыть, что оно равно четверти характерного расстояния, мы не знаем. Предположительно методом проб и ошибок. А как только они нашли расстояние, на которое следовало сдвинуть кол, очень простое правило значительно улучшило работу обсерватории. А именно: отложите расстояние G от середины между двумя кольями, установленными при двух последовательных заходах Луны, ближайших к максимальному склонению, и примите полученную точку в качестве указателя месячного максимума, если она окажется левее кольев. Если же нет, примите за такой указатель левый кол пары. Максимальная ошибка при следовании этому правилу составляет G/4 — в случае Темпл-Вуда около 5 м. В первое время использования обсерватории такой приближенный метод вполне мог дать толчок к постепенному улучшению способа экстраполяции.

Но по мере накопления опыта выявилось бы, что этого правила недостаточно. И может быть, пришла пора, когда было повторено магическое заклинание и отложено еще одно расстояние влево, на этот раз от пары левых кольев — одного из первоначальной пары и кола, установленного в результате откладывания первого расстояния G. Если в первой стадии экстраполяции было обнаружено, что число 4 имеет особое значение, то можно ли было выбрать расстояние лучше, чем снова разделив предыдущее расстояние на 4 и отодвинув кол влево на G/4? Такая процедура дает положение четвертого кола несколько левее остальных, и хотя древние наблюдатели, вероятно, не понимали, почему это так, он оказался бы уже очень близко к положению, соответствующему наибольшему склонению за данный месяц.

Чем это объясняется, мы можем увидеть, взглянув на рис. 7.4, сходный с рис. 7.3, но упрощенный, чтобы избежать путаницы со всеми лишними линиями. Положения кольев для двух заходов Луны представлены точками P₁ и P₂; точка P₃ дает положение третьего кола на расстоянии G от середины между точками P₁ и P₂. Откладывая G/4 от середины между точками P₁ и P₃, мы находим точку P₄. Согласно свойствам параболы, точка P₄ также лежит на ней, но ближе к вершине, чем P₁ или P₃. После этого этапа максимальная ошибка составляет G/4. При желании можно было бы еще раз повторить ту же процедуру и отложить G/16 от середины между P₁ и P₄, чтобы найти положение пятого кола P₅. Если в какой-то момент новый кол не окажется левее одного из прежних, мы останавливаемся и используем самый левый кол как маркировочный кол для данного месяца. В любом месте три этапа должны дать достаточную точность, поскольку наибольшая ошибка не превысит G/16, что соответствует изменению склонения примерно на 1/70°.

Рис. 7.5. Как определить p2/(4G) с помощью веревок и измерительных реек. ED/AD = CB/AB, поэтому ED/p = p/(4G) и ED = p2/(4G)

Однако, хотя этот метод и дает точные результаты, а все сопряженные с ним сложности исчерпываются умением складывать веревку и вбивать в землю колья, у нас нет никаких доказательств того, что он использовался в раннем бронзовом веке. Даже если мы находим расстояние G или 4G, воплощенные в геометрии данного памятника, это вовсе не означает применение именно данного метода, поскольку существует несколько других способов экстраполяции, при которых также могли использоваться такие расстояния. Некоторые памятники, например в Кейтнессе и в Дартмуре, демонстрируют странное расположение камней, в котором имеются производные от характерных для них G, что указывает на более сложный метод экстраполяции, чем описанный выше. Эти другие методы не ведут к правильной экстраполяции расстояния через ряд последовательных приближений, но дают экстраполируемое положение более непосредственно, путем откладывания определенного расстояния либо от середины между кольями, либо от более дальнего кола в паре.

Чтобы легче разобраться в таком методе, мы используем следующие обозначения. Половину расстояния между двумя кольями принято обозначать буквой p, так что полное расстояние между ними равно 2p. Нетрудно доказать (доказательство это приводится в приложении A), что расстояние, которое следует отложить от середины между двумя левыми кольями, равно G + p²/(4G). Если мы попробуем проверить это уравнение, приняв p = 0 (колья соприкасаются), то получим в результате G, а если мы возьмем p = 2G (максимальное возможное расстояние между кольями), то искомое расстояние составит G + (4G²/4G), что после преобразований дает 2G. Это именно те величины, которые графически выводятся на рис. 7.3. Измеренное от левого кола пары расстояние это равно G + (p²/4G) − p. Выражение p²/4G часто обозначается греческой буквой «эта» — η, так как для величины, постоянно фигурирующей в книгах и статьях на эту тему, удобнее обходиться одним символом.

Рис. 7.6. Второй вариант использования треугольника для экстраполяции расстояния. ED/AD = CB/AB, поэтому ED/(4G − p) = p/(4G) и ED = (4G − p)p/(4G) = p − η

Оставим пока в стороне вопрос о том, как люди раннего бронзового века могли прийти к этому решению, и зададим естественный вопрос: нет ли способа найти G + η или G + η − p с помощью чертежа на земле, без современной математики? Профессор Том в одной из своих книг показал, что это вполне возможно сделать с помощью веревок и измерительных реек. Рассмотрим треугольник на рис. 7.5. Здесь AB — это расстояние 4G для данного астрономического направления, полученное из предыдущих наблюдений. Два захода Луны при недавнем месячном максимуме склонения дали нам расстояние 2p, и мы откладываем отрезок p перпендикулярно линии AB в точке B — это линия BC. Теперь мы отложим отрезок p от A и, найдя точку D, построим в ней еще один перпендикуляр к AB. Точку, в которой эта линия пересечет веревку, соединяющую A и C, обозначим буквой E. Расстояние DE = η, как видно из чертежа. Этот метод применим в любой лунной обсерватории, где 4G известно достаточно точно, с ошибкой не более 10%.

Существуют и более изящные способы применения этого исходного метода экстраполяции, когда колья, установленные во время наблюдения, могут быть прямо введены в искомый треугольник. При этом используется вариант схемы, показанной на рис. 7.5. Отложив отрезок p не от A, а от B (рис. 7.6), получаем отрезок DE, равный не η, а p − η. Применить эту идею к обсерватории вроде Темпл-Вуда очень легко.

Соответствующие части обсерватории Темпл-Вуд показаны на рис. 7.7, где горизонтальная линия соответствует направлению S₁S₃, а керн Y находится вверху. Точки P₁ и P₂ — положения двух кольев, установленных в результате наблюдений двух последовательных заходов Луны вблизи времени максимального склонения. Веревка длиной 2p складывается пополам, чтобы получить положение среднего кола P₃. Затем один конец веревки закрепляется у P₁, а другой захлестывается за P₃ и поворачивается, пока не окажется на линии, проведенной к керну Y. У этого ее конца вбивается еще один кол E. Теперь надо найти положение пятого кола D, что достигается визированием в двух направлениях: от P₁ на керн Y и от E на выемку холма Белланох на горизонте. (Отсюда DE параллельно P₁P₂.) Затем веревка снимается, один ее конец закрепляется у D, а второй заводится через E и P₃ к точке F на линии P₁P₂. Поскольку DE равно p − η, как это показано на рис. 7.6, а длина веревки составляет 2p, отрезок P₃F должен равняться η. Для завершения экстраполяции остается только отложить известное расстояние G от точки F до точки A, которая и указывает, где надо было бы стоять, чтобы увидеть, как Луна заходит в выемку при максимальном месячном склонении.

Рис. 7.7. Возможный метод экстраполяции на лунной обсерватории Темпл-Вуд

Применение этого метода экстраполяции в Темпл-Вуде позволяет заметить две интересные особенности. Направление от главного менгира S₁ к керну Y не перпендикулярно линии кольев (рис. 6.9). Это не имеет никакого значения при условии, что линия DE ей параллельна. Далее, поскольку кол P₃ от месяца к месяцу должен занимать на линии разные места, расстояние P₁Y, принимаемое за 4G, также будет слегка меняться. Расстояние P₃Y мало зависит от смещения кола P₃ — в какой бы точке между менгирами S₃ и S₄ он ни находился, изменения расстояния P₃Y не превысят 10%. Как мы уже говорили, для величины 4G это вполне приемлемая точность.

То, что сохранилось на земле в Темпл-Вуде, не позволяет установить, какой из этих методов экстраполяции был там применен — да и вообще был ли там применен хоть какой-то метод экстраполяции. Для того чтобы найти памятники, где уцелевшие камни подсказывают, как могла быть осуществлена экстраполяция, нам надо отправиться в графство Кейтнесс, в самой северо-восточной части Шотландии. В этой отдаленной части Британских островов, в небольшой области, от 10 до 25 км к юго-западу от города Уика находятся четыре довольно странных памятника — в Мид-Клите (фото XXII), Дерлоте, Лох-оф-Яр-роусе и Камстере. Все это, по-видимому, были лунные обсерватории с обычным отмеченным камнями ближним визиром и выемками на горизонте в направлениях, соответствующих восходу или заходу «высокой» и «низкой» Луны. Любопытной особенностью, отличающей их от лунных обсерваторий в других частях страны, являются веерообразные ряды небольших камней, расположенные поблизости от них. В основе расположения этих вееров лежит решетка, и камни отмечают пересечения продольных и поперечных ее линий (рис. 7.8). Линии эти сближаются, хотя и не доведены до точки, где они могли бы сойтись. Во всех четырех памятниках веерообразные системы сопоставимы по размерам: самая большая (в Дерлоте) имеет 45 м в ширину и 42 м в длину, а самая маленькая (в Лох-оф-Ярроусе) 15 на 40 м, хотя очень вероятно, что тут большая часть веера была уничтожена при распашке. Камни разделены интервалами от 2 до 2,5 м, и во всех четырех веерах интервалы в продольных и поперечных рядах одинаковы.

К сожалению, на протяжении веков все эти памятники очень пострадали от расчистки земли, а растительность, разросшаяся около небольших камней, совсем их скрывает. В Мид-Клите, наиболее сохранившемся из них, все еще насчитывается более 200 низких, менее метра, плит, забутованных у основания мелкими камнями. Плиты ориентированы вдоль ряда. Мид-Клит сложнее остальных трех памятников, потому что к западу от основного сектора у него есть дополнительный веер, ряды которого в середине странно изогнуты. Судя по камням, разбросанным к востоку от главного веера, там мог находиться еще один дополнительный веер. Большой веер имеет ширину у основания 40 м и сужается до 24 м, причем длина рядов составляет 44 м. Радиус главного веера равен 110 м, а дополнительного — 126 м. Ось главного веера отклоняется от истинного севера на 1,5°.

Камни установлены на пологом склоне холма, и узкий конец веера почти достигает гребня, который тянется в направлении восток—запад. Вдоль этого гребня лежат еще камни, включая большой упавший менгир длиной 2,7 м, остатки маленького керна и т. д. Профессор Том предположил, что этот гребень является линией, которой пользовались наблюдатели, размечая два лунных направления — точки восхода Луны на юго-востоке при склонении −(ε + i) и на северо-востоке при склонении +(ε + i). В обоих направлениях на горизонте есть небольшие выемки — восход при склонении −(ε + i) отмечен выемкой в целых 80 км от места наблюдения. Выемка, отмечающая место другого восхода, находится на расстоянии 2,9 км. Ни то, ни другое направление в пределах памятника на земле четко не обозначены, хотя внешний ряд дополнительного веера направлен на северо-восточную выемку, и профессор Том отметил, что если в свое время действительно существовал еще один дополнительный веер, расположенный симметрично первому, его внешний ряд указывал бы второе направление.

Рис. 7.8. План рядов в Мид-Клите с наложенной схемой геометрической интерпретации по А. Тому. Единица L сетки равна 20/7 м. ярда = 2,37 м. По рисунку из книги А. Тома Megalithic Lunar Observatories

Отдаленная выемка едва ли была удобным лунным визиром, и не только потому, что ее использование возможно только при исключительно хорошей видимости, но и из-за того, что она требует очень больших перемещений — расстояние, соответствующее 4G, для нее составило бы около 1000 м. С другой стороны, длина гребня вполне достаточна для того, чтобы обеспечить положения при наблюдении захода и верхнего, и нижнего края лунного диска, и положения эти могли бы служить в течение нескольких лет до и после момента «высокой» Луны.

По мнению профессора Тома, эти каменные веера были созданы в качестве вычислительных устройств для решения проблемы экстраполяции. Они могли действовать как треугольник с одной стороной, равной 4G, который сразу дает расстояние, позволяющее найти длину ε. Эти постоянные веера имели перед методом треугольника то преимущество, что не требовали установки кольев с помощью визирования от дальнего конца базовой линии длиной в 4G. Наблюдатель должен был отмерить расстояние p от угла B веера в двух направлениях, как показано на рис. 7.9, а затем найти E по продольным и поперечным рядам камней. Расстояние DE равно p − ε точно так же, как и на рис. 7.6, и его тоже пришлось бы отмерить с помощью веревки. Следовательно, самый непосредственный способ найти экстраполируемое положение таков: отложите длину p − ε вдоль линии поставленных за последние ночи маркировочных знаков, от самого крайнего до ближайшего к нему. Поставьте тут временный кол и отложите от него расстояние G в противоположном направлении, т.е. в направлении крайнего маркировочного знака. Это эквивалентно тому, чтобы отложить все расстояние G + ε − p от кола, установленного во время наблюдения Луны при максимальном склонении. Когда мы задумываемся над тем, каковы же должны были быть размеры каменных вееров, выявляется любопытная возможность. В первый момент нам представляется, что, поскольку максимальное значение p равно 2G, это и есть минимальная длина продольных и поперечных рядов. Однако дело обстоит иначе: ведь будь их длина точно равна G, они все равно работали бы, даже когда величина p превышала бы длину и ширину веера. Камни в этом случае можно было использовать точно таким же способом: когда величина p оказывается больше G, ее откладывают, как и раньше, от угла B (рис. 7.9), но конец веревки заводится за последний камень продольного или поперечного ряда и протягивается в обратном направлении. Конец веревки, как и раньше, обозначает расстояние BC и BD, но величина, отмеренная теперь по сторонам веера, равна 2G − p. На рис. 7.9 геометрически доказано, что расстояние DE равно теперь не p − ε, а G − ε. В таком случае искомое положение можно найти, отмерив от середины между поставленными в две следующие друг за другом ночи кольями расстояние DE назад от крайнего кола, а затем отложить 2G в противоположном направлении. Использование такого довольно тонкого варианта метода экономит массу труда при установке вееров, так как необходимая их площадь становится вчетверо меньше.

Гипотеза профессора Тома о том, что каменные веера создавались как вычислительные устройства раннего бронзового века для разрешения проблемы экстраполяции, имеет далеко идущие последствия. Если он прав, его гипотеза весьма действенно поддерживает всю концепцию астрономии бронзового века и, в частности, делает гораздо более правдоподобным использование метода экстраполяции с помощью треугольников. А потому мы должны очень тщательно рассмотреть параметры каменных вееров и взвесить данные, как подтверждающие, так и опровергающие идею профессора Тома.

Рис. 7.9. Метод экстраполяции с помощью каменных вееров. Первый метод использования. Пусть BC = BD = р. Тогда поскольку ED/AD = CB/AB, ED/(4G − p) = p/(4G), откуда ED = (4G − p)p/(4G) = p − ε. (Cp. с рис. 7.6). Второй метод использования. Пусть BC = BD = 2G − p. Тогда ED/[4G − (2G − p)] = (2G − p)/(4G), откуда ED = (2G + p)(2G − p)/4G = (4G² − p²)/(4G) = G − ε Рис. 7.9. Метод экстраполяции с помощью каменных вееров. Первый метод использования. Пусть BC = BD = р. Тогда поскольку ED/AD = CB/AB, ED/(4G − p) = p/(4G), откуда ED = (4G − p)p/(4G) = p − ε. (Cp. с рис. 7.6). Второй метод использования. Пусть BC = BD = 2G − p. Тогда ED/[4G − (2G − p)] = (2G − p)/(4G), откуда ED = (2G + p)(2G − p)/4G = (4G2 − p2)/(4G) = G − ε

Что мы хотим обнаружить? В первую очередь — что веера расположены неподалеку от памятников, которые могли быть лунными обсерваториями. По утверждению профессора Тома, все четыре каменных веера отвечают этому условию. Радиус сектора должен иметь ту же длину, что и расстояние 4G для связанного с ним астрономического направления. Длина и ширина сектора должны быть примерно одинаковыми и, чтобы отвечать всем возможным значениям р, равняться точно G или хотя бы 2G. Интервалы между камнями роли не играют, хотя, несомненно, удобнее, если они одинаковы и в продольных, и в поперечных рядах.

Размеры четырех известных каменных вееров приведены в табл. 7.1, данные для которой взяты из гл. 9 книги профессора Тома «Мегалитические лунные обсерватории». (Вычисленные значения 4G на несколько процентов больше приведенных тут, так как уменьшение склонения Луны за 24 часа известно теперь точнее, чем во время работы Тома над книгой.) Памятники расположены в порядке уменьшения числа уцелевших камней, так как по этому признаку и следует судить о их доказательной ценности.

Таблица 7.1. Главные размеры каменных вееров

Мид-Клит и Дерлот оба отвечают критерию, требующему, чтобы длина и ширина сектора были примерно одинаковыми; рассматривать остальные два в этом отношении не имеет смысла — слишком много камней исчезло. Согласие между радиусами секторов и вычисленными значениями 4G удовлетворительно для Дерлота и Лох-оф-Ярроуса, и даже в Камстере сектор можно было бы использовать для экстраполяции 4G, несмотря на то что он процентов на двадцать короче, чем требовалось бы. Ранее в этой главе, говоря о методе экстраполяции с помощью треугольников, мы отметили, что в идеале значение 4G следовало бы определять с ошибкой не более 10%. То же относится и к секторному методу, но ошибка в 20% не причинила бы наблюдателям непреодолимых затруднений. Ошибка зависела бы от точности работы при использовании веера. Когда p меньше G, значение, даваемое сектором для p − η, было бы слишком мало. Если наблюдатели определяли экстраполируемое положение, откладывая p − η от дальнего кола, а затем в противоположном направлении, то обе ошибки отчасти компенсировали бы друг друга. Для большинства значений p ошибка окончательного экстраполированного положения не превышала бы 0,1G, что соответствует ошибке в азимуте на 1/40°.

Мид-Клит труднее всего поддается удовлетворительному объяснению, а ведь он сохранился лучше остальных. Как видно из табл. 7.1, радиус главного веера составляет 65% от вычисленного значения 4G. Это почти безусловно недопустимое отклонение. Величина 4G рассчитывалась на основе предположения, что маркировочная линия была перпендикулярна астрономическому направлению, но, судя по расположению памятника, это представляется маловероятным. Наблюдателям в этом случае приходилось бы работать на очень неудобном склоне и было бы куда легче оставаться на ровной вершине гребня. Линия маркировочных кольев легла бы тогда под углом 63° к астрономическому направлению, а расстояние 4G вдоль этой линии равно 191 м. Радиус же главного сектора составляет от 191 м только 58%.

Несмотря на столь большие ошибки в радиусе главного сектора, экстраполированные положения при значениях p вплоть до 1,5G удивительно близки к правильным. Читатель может без труда это проверить, использовав выполненный в масштабе чертеж сектора и принимая для p разные значения. Если мы проделаем это и попробуем найти p − η по сектору, приняв для откладывания вдоль линии кольев значение 4G, равное 44 м (т. е. длину базы сектора, а не одну четверть его радиуса), то обнаружим, что самая большая ошибка в определении экстраполированного положения при любых значениях p составит все-таки менее 0,1G. Получаемая при этом точность азимута совершенно достаточна для использования обсерватории.

Хотя каменные веера Мид-Клита могли вполне удовлетворительно функционировать в качестве вычислительной машины для экстраполяции, мы не должны закрывать глаза на связанные с ними несоответствия. Поскольку по наблюдениям в течение трех ночей относительно нетрудно определить величину 4G, странно, что радиус настолько неточен. Какое-то объяснение этому можно найти в топографии местности. За гребнем склон уходит к северу вниз, и лишь от очень немногих поперечных рядов можно увидеть местоположение центра сектора. Это должно было усложнить его распланирование, но в раннем бронзовом веке разрешались и не такие геометрические трудности.

Дополнительный веер к западу от основного имеет чуть больший радиус — 126 м, но и это еще гораздо меньше 4G. Этот малый сектор слишком узок для экстраполяции, и его назначение остается неясным. Изгиб в середине придает ему сходство с каменными рядами Бретани в Ле-Менеке и Кермарьо.

Многие археологи относятся к предложенному профессором Томом объяснению более чем сдержанно. Они могли бы указать, что известно только четыре таких веера, причем два из них сохранились очень плохо. Веера двух лучше сохранившихся памятников выглядят более или менее убедительно, только когда линии предполагаемых решеток уже наложены на план, но это далеко не так, если на нем показаны только камни. И наконец, размеры сектора в Мид-Клите довольно сильно отличаются от ожидавшихся, и тот факт, что они все-таки подходят для экстраполяции, может быть простым совпадением. С другой стороны, все каменные веера как будто расположены неподалеку от отмеченных лунных направлений, имеют примерно подходящие размеры и других объяснений для них пока не предложено. Обе стороны, несомненно, согласятся с тем, что наше понимание этих памятников намного улучшилось бы, если бы в одном из них были проведены раскопки, которые дали бы возможность составить более полный план расположения камней. Хотя их можно было бы использовать для экстраполяции, из одного этого вовсе не следует, что их действительно так использовали. Но до тех пор, пока не будет выдвинута более убедительная гипотеза, можно, не выходя из пределов разумного, предположить для них такое назначение и взвесить, какие последствия вытекают из этого для наших представлений о раннем бронзовом веке.

Каменные ряды на Британских островах имеются не только на северо-востоке Шотландии. Они встречаются в разных районах страны, но крупнейшее их скопление находится в Девоншире, на Дартмурских пустошах, где известно около шестидесяти рядов — одиночные, двойные и даже несколько тройных. Самые короткие имеют в длину примерно 30 м, а самые длинные тянутся более чем на 3 км. Сформулировать общие правила, приложимые ко всем рядам, невозможно, но есть некоторые предположения, выглядящие достаточно правдоподобно. Ориентация рядов как будто определяется особенностями местности, так как они часто следуют направлению минимального уклона. Многие связаны с кернами, причем некоторые завершаются кернами с одного конца, а в одном случае — в Мерривейле — керн находится в середине двойного ряда. Ряды иногда кончаются большими поперечными камнями, и там, где ряд двойной, этот поперечный или блокирующий камень поставлен между рядами. Многие ряды состоят из мелких неправильной формы камней, менее 0,5 м в высоту, или из мелких плит. Эти последние всегда ориентированы вдоль ряда. В большинстве своем ряды довольно прямые (хотя и не вполне), однако некоторые из более длинных словно бы бесцельно извиваются по пустоши.

Каменные ряды Дартмура были известны любителям древностей еще с XVIII в., и их назначение порождало множество догадок. После выхода в свет книги Локьера об астрономически значимых направлениях в Стоунхендже и в других памятниках каменные ряды, естественно, тоже начали изучаться для проверки, не содержат ли они астрономически значимых направлений. Никаких четких указаний на это выявлено не было, хотя в Дартмуре несомненно можно обнаружить солнечные и лунные направления, связанные с кольцами и кернами. Исследование каменных памятников, проведенное профессором Томом, открыло новые возможности — ведь теперь ясно, что ряды все-таки могли быть связаны с астрономическими наблюдениями и не будучи ориентированы на какую-то определенную точку лунного восхода или солнечного захода. Исходя из этого, Ален Пенни и я в 1974 г. исследовали каменные ряды в Мерривейле.

Остальная часть этой главы будет посвящена подробному описанию Мерривейла, поскольку он — прекрасный пример очень сложного памятника, сочетающего в себе ряды, керны, мегалиты и каменные кольца. Он показывает, насколько тесно могут быть связаны между собой геометрические и астрономические аспекты. Кроме того, это один из важнейших памятников на юге Англии, как давно признали археологи, хотя туристам он известен относительно мало. А между тем он относится к числу наиболее доступных памятников бронзового века Дартмура, так как расположен чуть южнее шоссе из Ашбертона в Тависток, примерно в 4 км от Принстауна.

Находится он на практически ровной возвышенности, покрытой обычной для этих пустошей растительностью. Вероятно, первоначально тут было поздненеолитическое кладбище, поскольку к югу от каменных рядов видны две гробницы, характерные для этого периода. Они никак не связаны с остальными имеющимися там остатками древних сооружений. Среди этих последних есть сильно разрушенный керн, от которого сохранилась в основном эллиптическая подпорная стенка размерами 19 на 16 м (эксцентриситет 0,086). Он, по-видимому, также относится к более раннему периоду.

Каменные ряды (рис. 7.10) сохранились почти полностью — два двойных ряда, ориентированных примерно в направлении восток—запад и почти параллельных. В западном конце обоих рядов камни крупнее, а восточный у обоих замыкается блокирующим камнем. Посередине южного более длинного ряда II есть керн, окруженный яйцеобразным кольцом типа I (фото XXI). К западу от этого керна короткий одиночный ряд тянется на юго-запад от другого керна. Вокруг в пределах памятника разбросано еще несколько небольших кернов высотой не более 0,25 м и менее 6 м в диаметре. Они считаются могильниками бикеров, и их можно датировать примерно 2300 г. до н. э. Камни у одного из концов ряда III сложены в виде керна, и потому археологам известно, что этот маленький ряд был сооружен не ранее бикеровского периода.

Рис. 7.10. План каменных рядов в Мерривейле. Камни в рядах расположены так тесно, что их нельзя показать по отдельности

Как показано на рис. 7.10, к северу и к югу от рядов есть каменные кольца. Северное представляет собой правильный круг диаметром 8,6 м, а южное — приплюснутый круг типа Б (фото XX) диаметром 20,55 м и малой осью, ориентированной в направлении север—юг. В нем чередуются округлые и плоские камни, как в некоторых других памятниках и, в частности, в Кеннетской аллее. На расстоянии чуть больше 40 м от центра приплюснутого круга, прямо на юг от него находится большой стоячий камень высотой 3,15 м, и из-за его соседства с кольцом профессор Том предположил, что он был установлен там сознательно, как указатель меридионального направления. Это был первый намек на то, что Мерривейл мог иметь астрономическое назначение. Точно на линии между этим менгиром (менгир I) и восточным концом ряда II находится большая каменная плита (плита I), длинная сторона которой перпендикулярна этой линии, а в нескольких метрах в стороне — еще одна плита (плита II), ось которой параллельна этой линии. Кроме того, есть еще два менгира к югу от каменных рядов и четвертый к северу от ряда I.

Оба двойных ряда очень похожи. Параллельные линии камней почти, хотя и не совсем прямые, и расстояние между линиями колеблется от 0,8 до 1,3 м в ряду I и от 0,6 до 1,2 м в ряду II. Оно настолько мало, что выдвигаемая иногда гипотеза, будто ряды должны были служить церемониальными путями, выглядит совершенно неубедительно. Ряд I, ориентированный по азимуту 83,7°, имеет в длину 181,7 м и включает 186 камней, хотя видны они теперь не все, поскольку самые мелкие, а также упавшие камни закрыл торф. Большинство видимых камней поднимается над землей менее чем на 0,4 м — эффектным зрелищем Мерривейл назвать никак нельзя. Концевые камни A и B на рис. 7.10 относительно высоки — до одного метра, а три камня в рядах, в точках V, W и X, также заметно выше остальных. Интервалы между камнями по всему ряду примерно одинаковы и в среднем близки к 1,86 м.

Ряд II ориентирован по азимуту 81,7°, имеет в длину 263,7 м и включает 266 камней, если считать камни яйцеобразного кольца и несколько камней, погребенных теперь под землей. Опять-таки почти все камни мелкие, концы отмечены заметно более крупными камнями, и есть еще семь высоких камней (буквы от O до U на плане). Интервалы между камнями, хотя и одинаковые в обеих линиях, в ряду II неравномерны: они больше в центральной части, между S и Q (2,24 м), и меньше в восточном конце, между R и E (1,12 м).

Таблица 7.2. Расстояния (в метрах) между большими камнями в рядах I и II

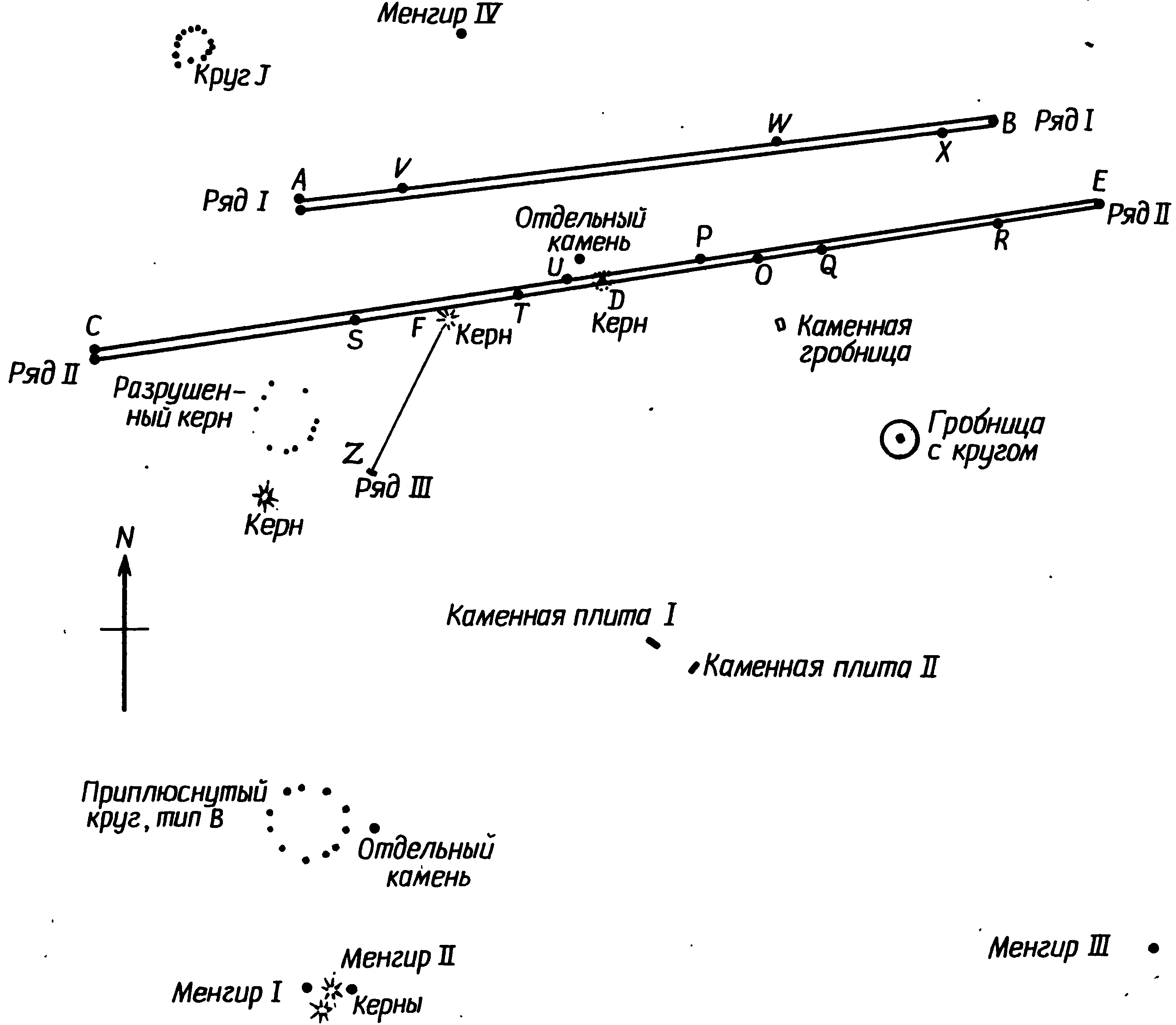
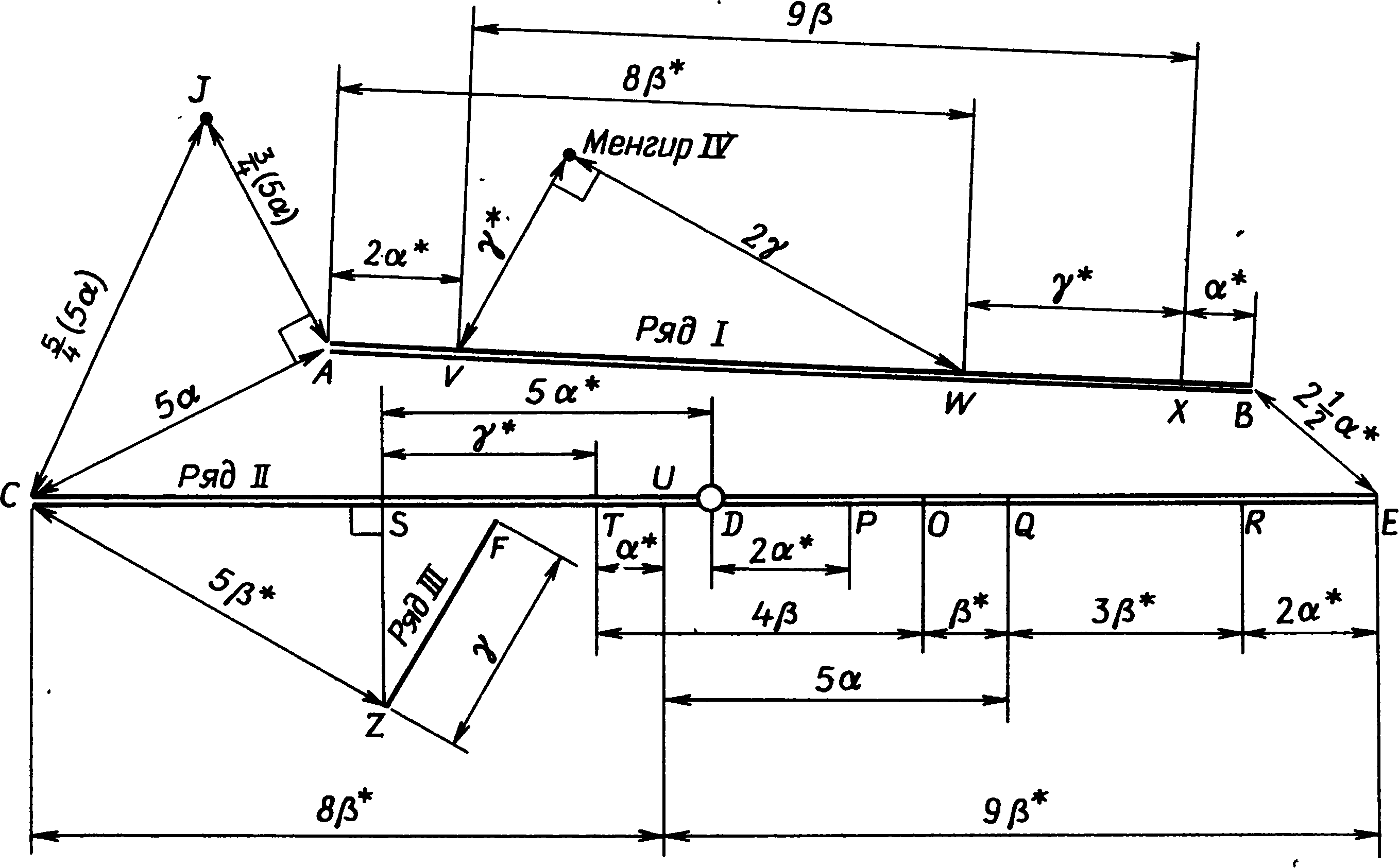
Ряд III состоит из одной линии, имеющей в длину 42,3 м и ориентированной по азимуту 23°, и включает 41 камень со средним интервалом между ними 1 м. Видны лишь немногие из этих камней, и мы уточняли положения остальных, снимая торф с их верхушек. Камни в концах ряда поставлены поперек, так что его длина не вызывает сомнений.

На первый взгляд расположение крупных камней в рядах представляется беспорядочным, но после измерения интервалов между ними выяснилось, что определенные расстояния повторяются по нескольку раз. Они приведены в табл. 7.2.

Система становится понятной, когда мы отдаем себе отчет, что все повторяющиеся расстояния кратны этим трем основным единицам длины. Я обозначу их греческими буквами α (альфа), β (бета) и γ (гамма) и дам им значения соответственно 13,1, 15,6 и 43,4 м. Если выразить приведенные в табл. 7.2 расстояния через единицы α, β и γ, мы получим результаты, приведенные в табл. 7.3. Интервалы оказываются не абсолютно строго кратными этих трех единиц, однако удивительно к ним близки. Наименее точное расстояние TU короче единицы α всего на 3%; в 11 из измеренных расстояний отклонения от простых кратных составляют менее 1%. Указанные отрезки отмечены на плане каменных рядов на рис. 7.11.

Взаимное расположение рядов II и III также определяется этими единицами. Длина ряда III почти равна; (FZ = 0,97 γ), а расстояние между западными концами рядов II и III — расстояние CZ — равно 5,01 β. Направление и длина ряда III таковы, что он образует с камнем S прямоугольный треугольник, т.е. CSZ — прямой угол. Угол CZF не совсем прямой, а равен 93°. Однако CZ и ZD имеют одинаковую длину с точностью до 1%, так же как ZF и FD. Это расстояние γ встречается в памятнике не менее шести раз, так как, кроме отрезков WX, ST, ZF и FD, ему равно расстояние от большого менгира I до центра сплюснутого круга и от камня V до менгира IV. Едва ли можно нагляднее продемонстрировать, что план этого памятника строился на какой-то исходной базе.

Таблица 7.3. Расстояния между большими камнями в рядах I и II (в единицах α = 13,1 м, β = 15,6 м и γ = 43,4 м)

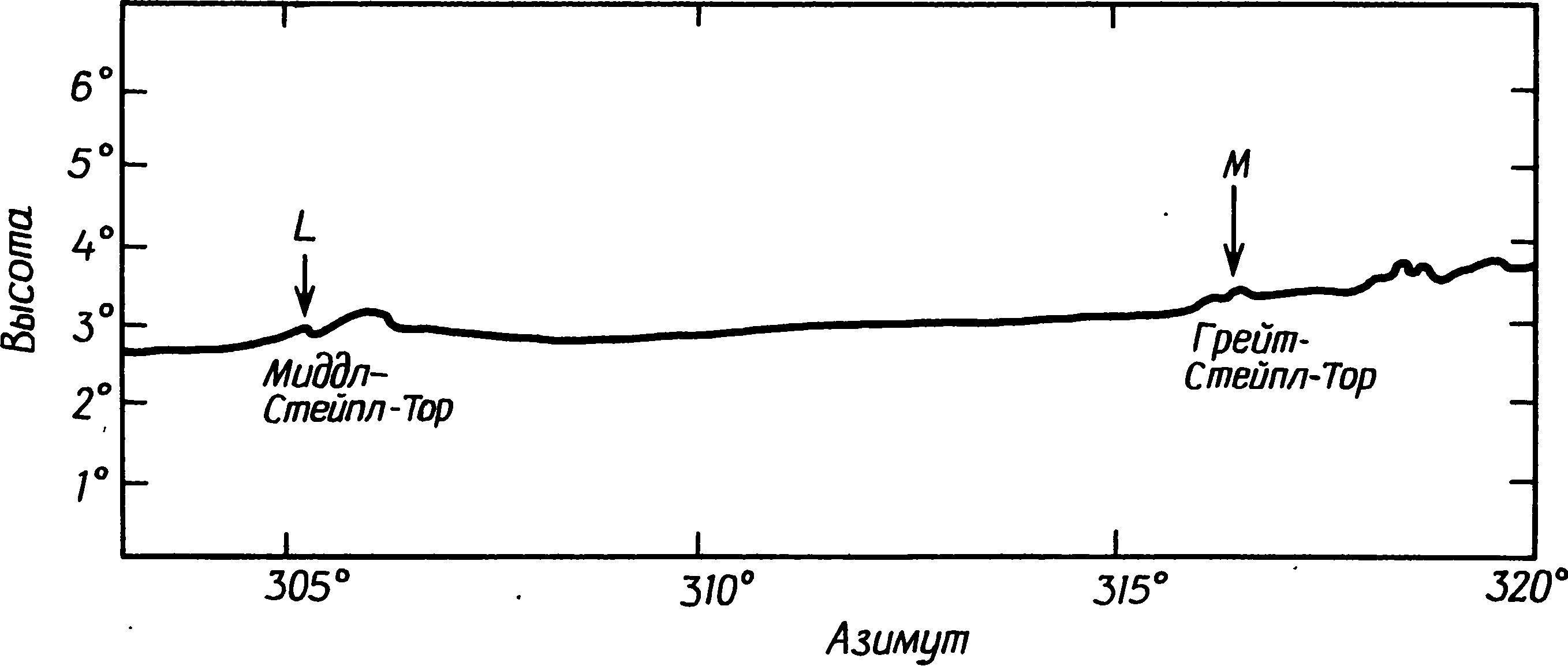
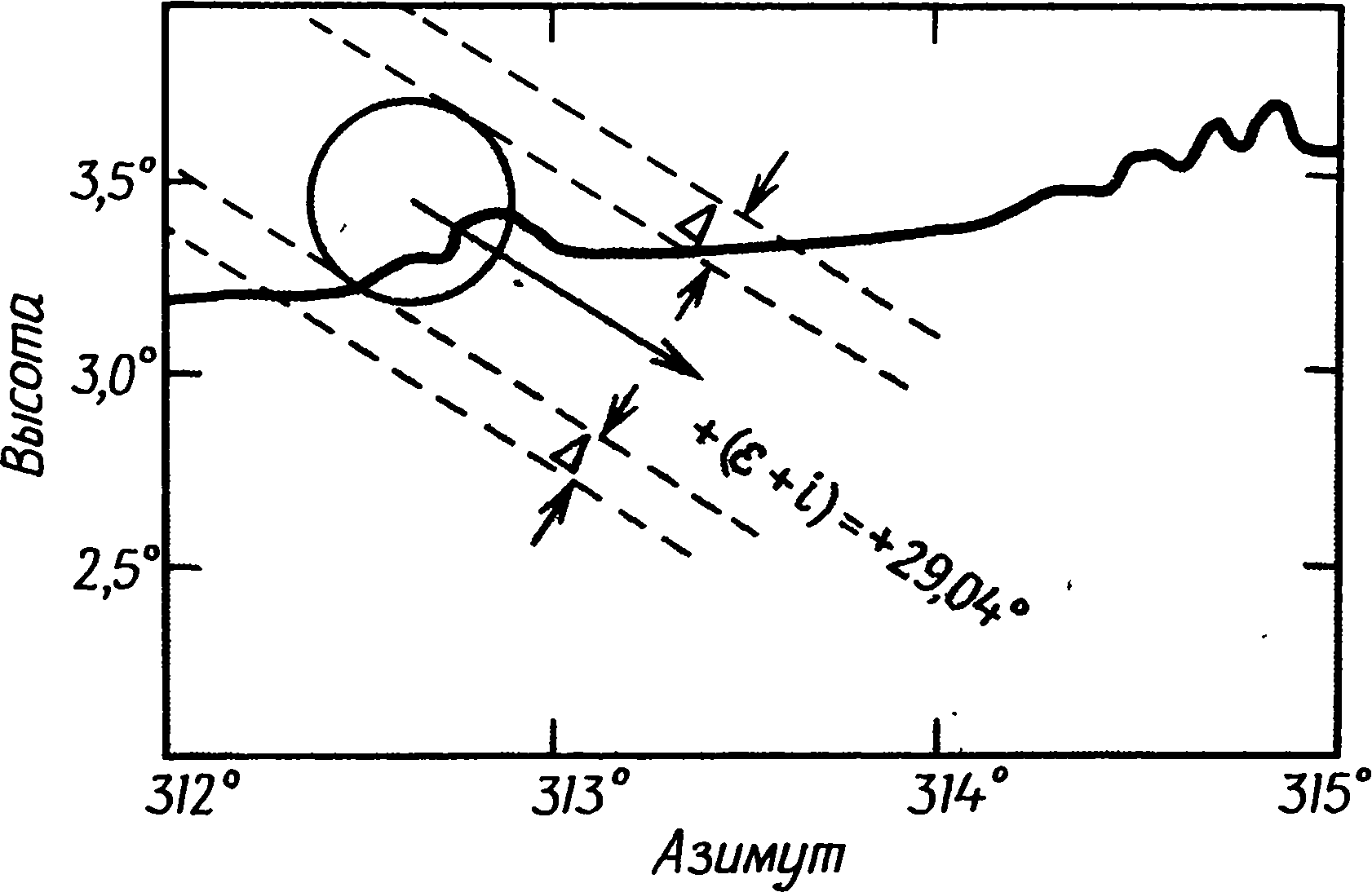
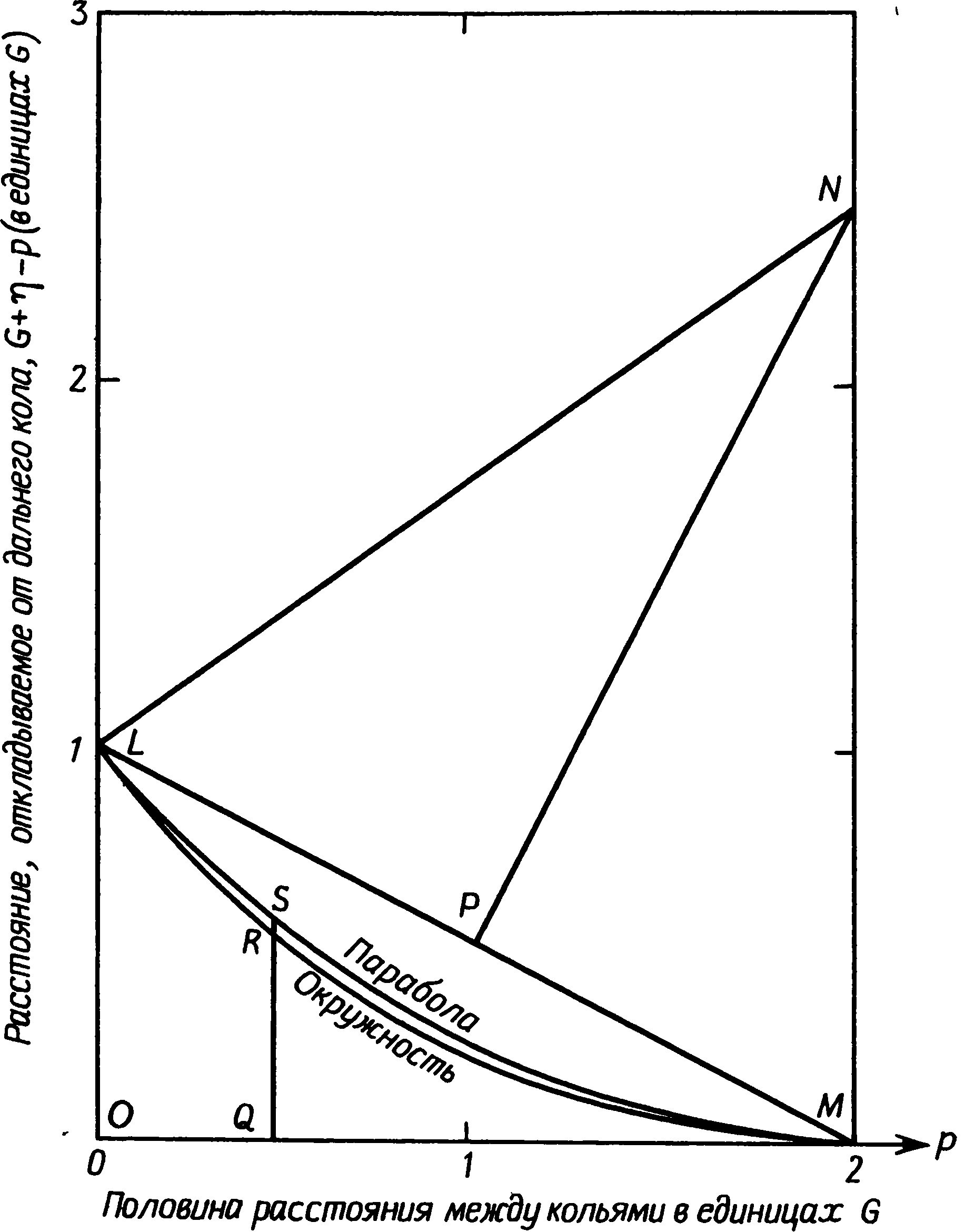
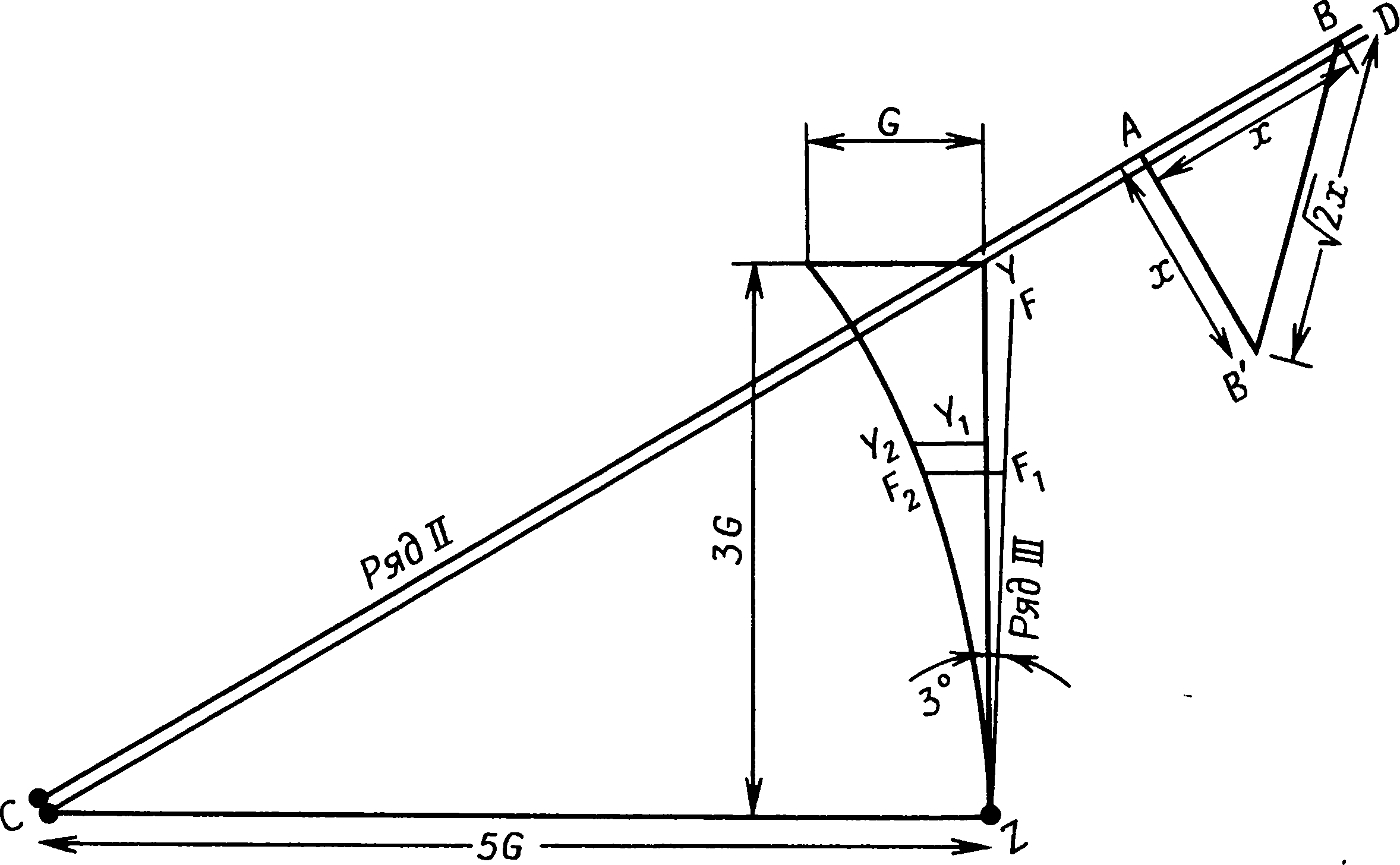
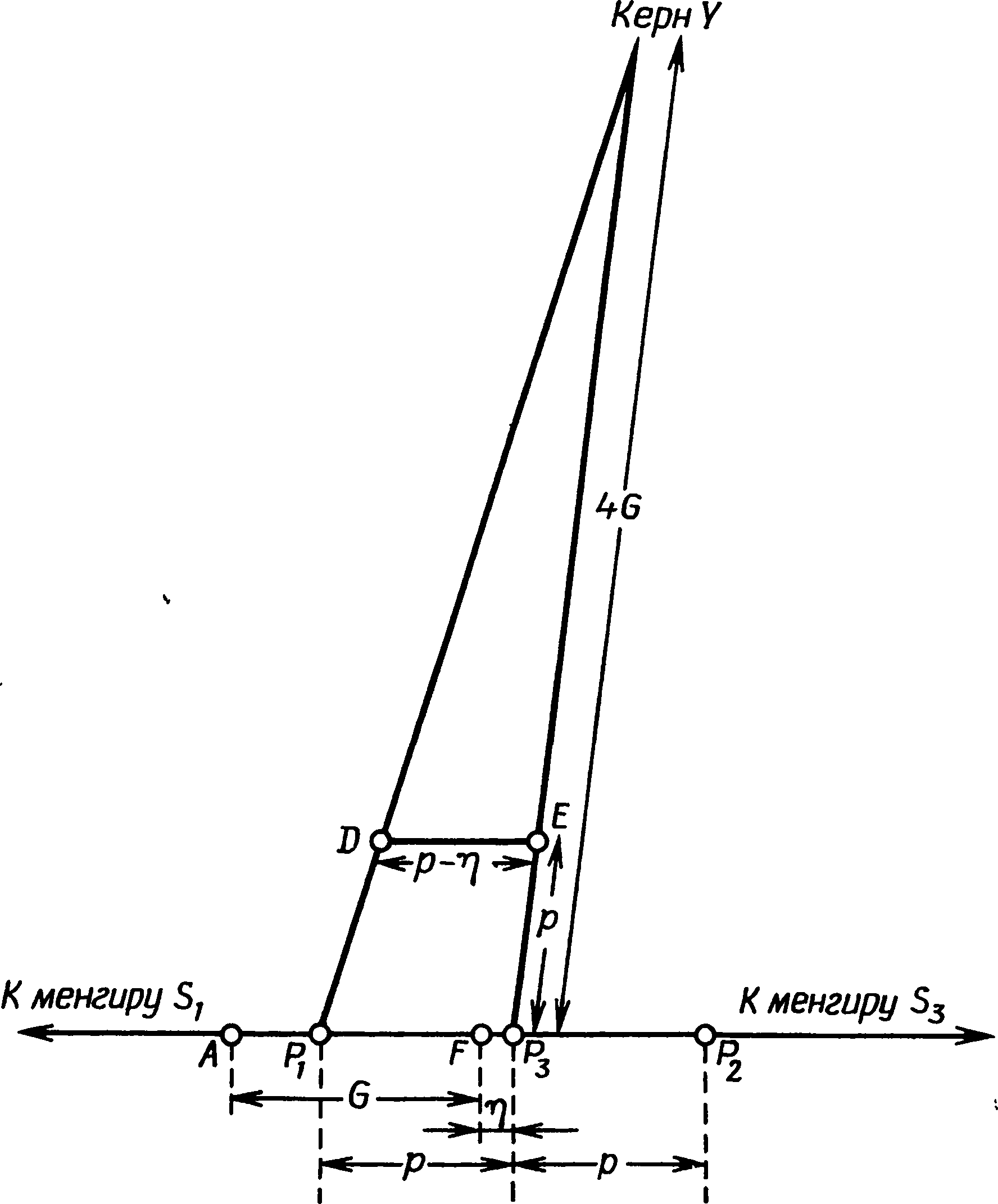
Однако мы еще не исчерпали любопытных геометрических особенностей Мерривейла. Менгир IV образует прямоугольный треугольник с камнями V и W ряда I. Два основных ряда связаны через расстояния между их концами, так как их западные концы C и A находятся в 5α друг от друга, а BE равно 2,5α. Круг J образует треугольник с отношением сторон 3:4:5 с A и C. Я уже упоминал, что плита I находится на прямой линии от менгира I к E; плита II уложена так, что образуется прямой угол C — плита II — B и еще один A — плита II — менгир I. Оба угла отличаются от прямого не более, чем на 1°.

Эти сложные и странные геометрические соотношения, многократно воплощенные в каменных рядах Мерривейла, не могут быть случайными. Имеют ли они какое-то особое значение или нет — дело другое, но представляется сомнительным, что они создавались лишь ради эстетического наслаждения самой геометрией, как дворцовые сады елизаветинского периода. Почему-то такое объяснение принимать не хочется — отчасти из-за того, что это прямо противоречит тому, как поступили бы мы в XX в. Нам нравится, чтобы наши технические сооружения имели определенное назначение, а потому мы ощущаем, возможно, без достаточных на то оснований, что у доисторических строителей должна была иметься веская причина, чтобы так устанавливать свои камни, пусть даже для нас она не всегда очевидна. Но, кроме того, мы знаем, что в других местах камни воздвигались с астрономическими целями, и, следовательно, имеем законное право проверить, не может ли этот памятник оказаться обсерваторией и не прольет ли это некоторый свет на тайны, скрытые в его геометрическом плане.

Рис. 7.11. Геометрические соотношения рядов камней в Мерривейле. Звездочка указывает, расстояния, которые могут быть выражены через α, β и γ с точностью лучше 1 м. Точность других расстояний лучше чем 1,5 м, за исключением CJ и AJ

Для дартмурского ландшафта характерны выходы гранита, разбросанные по пустошам точно огромные кирпичи. Несколько таких глыб видны на горизонте из Мерривейла, и, если бы целью строителей были астрономические наблюдения, было бы вполне естественно использовать их в качестве удаленных визиров. Наиболее интересна северо-западная часть горизонта, где имеются две заметные выемки (L и M на рис. 7.12), а еще чуть севернее видны хаотические нагромождения Грейт-Стейпл-Тора (фото XX). Вряд ли можно сомневаться, что этот сектор горизонта был важен для тех, кто пользовался Мерривейлом, поскольку выемка L очень четко указывается линией менгир III — плита II — плита I (последняя и сама указывает на ту же выемку). Насколько можно судить, центр разрушенного керна также лежал на этой линии. Направление на выемку M указано небольшим отдельно лежащим камнем к северо-западу от керна D. Для наблюдателя, стоящего в центре приплюснутого круга, Солнце в дни солнцестояний в позднем неолите и раннем бронзовом веке заходило бы за выемку L, а для стоящего в кольце J «высокая» Луна заходила бы за выемку M.

Эти направления можно было употребить для приблизительного определения движений Луны, но для достижения большей точности следовало бы применить метод, использованный в Темпл-Вуде, и производить наблюдения с линии, отмеченной на земле постоянно. Дополнительным и очень ценным улучшением этого метода было бы создание фиксированной шкалы расстояний так, чтобы линия практически превратилась в размеченную на пустоши гигантскую линейку.

Рис. 7.12. Северо-западная часть горизонта, видимая от кольца камней в Мерривейле. Расстояние до горизонта 1,6 км

Для этого было бы трудно придумать более удачное устройство, соответствующее технологии раннего бронзового века, чем каменные ряды Мерривейла. Видимая от конца A ряда I «высокая» Луна около 1800 г. до н.э. заходила бы так, как показано на рис. 7.13. Если бы наблюдатель стоял на линии где-нибудь еще, видимая точка захода Луны сместилась бы и в 7 м от конца ряда точно в выемке скрывался бы ее нижний край. По мере уменьшения ее склонения после максимума 18,6-летнего цикла наблюдатель, чтобы Луна по-прежнему заходила для него в выемке, должен был бы передвигаться вдоль ряда к западу. Длины ряда I достаточно, чтобы можно было вести наблюдения, пока склонение Луны не уменьшится до 26,4°, т. е. он может использоваться в течение пяти лет, пока Луна остается «высокой». Ряд II можно было использовать таким же образом. Для того чтобы увидеть, как Луна в максимальном склонении заходит в выемку, наблюдатель должен был встать около камня S. Все остальные наблюдения велись бы из положения между S и восточным концом E.

Техника наблюдений могла быть крайне проста. Возможно, их вели несколько человек из соседнего селения бронзового века, круги от хижин которого все еще видны на склоне холма менее чем в километре от каменных рядов. Их могли расставлять между линиями камней — по человеку на каждые два камня. В этом случае им велели бы тщательно следить, у каких камней ряда Луна будет в последний раз видна в выемке. Маркировочный камень для данной ночи клался бы рядом с тем, кто увидел, как Луна зашла в выбранной заранее точке горизонта. Как и в Темпл-Вуде, чтобы установить, в какой день месяца Луна имела максимальное склонение, наблюдения велись бы еженощно.

Рис. 7.13. Заход Луны, видимый от западного конца ряда I в Мерривейле

Эта обсерватория не могла бы работать вполне эффективно без каких-нибудь средств экстраполяции. Значения 4G могут быть вычислены для обоих рядов, и, хотя они несколько различаются для обоих рядов, среднее значение для памятника составляет 61,2 м, что дает G = 15,3 м. Это значение очень близко к длине единицы β, которая многократно повторяется в рядах, а потому весьма вероятно, что расстановка камней через промежутки, кратные β, производилась сознательно, с целью зафиксировать характерное расстояние всего сооружения.

Зная расстояние 4G, наблюдатели могли бы найти искомое положение для наибольшего склонения за месяц с помощью уже описанного выше метода последовательных приближений. Каменных вееров в Мерривейле обнаружено не было, но там имеются два прямоугольных треугольника (CZF и V — менгир IV — W) и естественно задать вопрос, нельзя ли использовать их для экстраполяции по методу, показанному на рис. 7.5 и 7.6. Мы знаем, что искомые положения можно находить с достаточной точностью, даже если сами треугольники не вполне точны. Треугольник CZF, правда, велик, но мог бы использоваться для этой цели; мы, однако, в этом сомневаемся, поскольку строители знали величину 4G и могли бы, если бы хотели, построить треугольник нужных размеров. Вместо этого они сделали одну из сторон равной точно 5G, и из этого следует, что, если они и использовали его для экстраполяции, их метод заметно отличался от того, который мы рассматривали в связи с шотландскими обсерваториями.

Продолжая исследование каменных рядов в Мерривейле, мы разработали возможный способ, при котором для экстраполяции используется короткий ряд III. Прежде чем людям бронзового века удалось решить эту задачу, они должны были бы провести много наблюдений заходящей Луны и вбивать колья вдоль рядов камней, отмечая, где надо встать, чтобы увидеть Луну, заходящую в выемку. К этому времени они уже должны были обнаружить, что для нахождения положения, соответствующего наибольшему склонению Луны, необходимо отложить некоторое экстраполируемое расстояние от крайнего левого кола. Они должны были обнаружить, что откладываемое расстояние оказывается наибольшим, когда два последних кола находятся близко друг от друга. Когда они отстоят друг от друга далеко, т. е. разделены характерным расстоянием 4G, никакого движения за левый кол не требуется. В прочих — промежуточных положениях наблюдатели не знали бы, какое расстояние нужно отложить, но они должны были осознать, что оно не находится в простой линейной зависимости от расстояния между кольями, поскольку, когда колья находились на половине максимального для них расстояния, расстояние, которое следовало откладывать от левого кола, не составляло половины своего максимума. Они должны были искать величину, которая была бы большой при малом расстоянии между кольями, очень быстро уменьшалась бы при раздвижении кольев и постепенно свелась бы к нулю при дальнейшем их раздвижении. Люди бронзового века, хорошо знакомые с геометрическими фигурами, вероятно, попытались бы воплотить эти измерения зримо в кривой, проведенной по земле.

Такое изменение можно довольно точно передать через измерение расстояния от касательной до дуги круга. На рис. 7.14 расстояние, откладываемое от левого кола, показано кривой LSM. По горизонтальной оси графика отложены различные значения половины расстояния между кольями, а откладываемое расстояние соответствует высоте кривой над этой осью. Следовательно, если половина расстояния между кольями равна OQ, расстояние, которое следует отложить, составляет QS. Кривая же LSM представляет собой отрезок параболы, а насколько нам известно, понятие параболы в раннем бронзовом веке известно не было. Однако люди той эпохи вычерчивали много окружностей, и кривая, которую они себе представили бы, скорее всего была бы дугой вроде LRM, составляющей часть окружности. В этом случае их задачей было бы найти ту окружность, которая дала бы наилучшие (ближе всего согласующиеся с точными) результаты, — найти, используя, возможно, только метод проб и ошибок.

Наша же задача — найти математическим путем радиус окружности, наиболее приближающейся к параболе, чтобы сравнить его с тем, что мы находим на месте, и проверить, нет ли там каких-либо данных, указывающих именно на такой подход к проблеме экстраполяции. Расчет «наиболее подходящей» окружности дан в приложении А; оказывается, есть несколько возможных ответов. Если мы отложим по оси OM половину расстояния между кольями, как на рис. 7.14, радиус составит 2,5G. Если мы отложим все это расстояние, радиус должен равняться 8,5G, а три четверти такого расстояния требуют радиуса в 5G. Это последнее решение довольно интересно, потому что только оно дает NM и OM, как кратные G — соответственно 5G и 3G.

Рис. 7.14. Экстраполяция от удаленной метки с использованием дуги круга

В Мерривейле имеется треугольник со сторонами 5G и 3G, геометрически связанный с рядом III. Я указывал (с. 170), что угол CZF равен 93° и, следовательно, непрямой. Начертив прямой угол CZY и поместив точку Y между камнями ряда II (рис. 7.15), мы обнаружим, что расстояние CY равно 46,4 м, а это лишь на 1% отличается от 3G. Если те, кто пользовался Мерривейлом, провели для постройки ряда III линию ZY, их метод экстраполяции мог быть таким:

а. Отложите с помощью веревки от Y в направлении Z три четверти расстояния между кольями, поместив маркировочный знак Y₁ у конца веревки.

б. Возьмите еще веревку длиной 5G, закрепите один ее конец в C, проведите дугу, чтобы найти точку Y₂ на пересечении дуги с перпендикуляром Y₁Y₂.

в. Отмерьте расстояние Y₁Y₂ от левого кола. Это и даст искомую позицию.

Однако точно таким способом они этого не делали. Судя по расположению памятника, так, по-видимому, была сделана первая экстраполяция, а затем метод был эмпирически изменен для увеличения точности. Используя дугу вместо параболы, они невольно вводили ошибку. Эту ошибку можно почти полностью исключить, переставив короткий ряд камней в положение ZF на рис. 7.15 и одновременно изменив ту долю расстояния между кольями, которая откладывается вдоль ряда. (Может быть, раскопки вдоль ряда III выявят систему более ранних лунок из-под камней или из-под столбов.) По длине ряда III мы можем установить, какую долю расстояния между кольями откладывали они в действительности, потому что, если это расстояние равнялось 4G, они должны были отложить вдоль ряда III всю его длину. Несколько неожиданно эта часть оказалась равной √(2/2). Не следует пугаться появления корня квадратного из двух — найти его геометрическим путем очень просто, и люди раннего бронзового века видели бы в нем просто длину третьей стороны равнобедренного прямоугольного треугольника. Метод экстраполяции с использованием ряда III в его нынешнем виде выглядит так:

а. Если два кола занимают положения, обозначенные на рис. 7.15 точками A и B, возьмите веревку длиной AB и натяните ее так, чтобы она легла вдоль AB′.

б. Теперь возьмите другую веревку длиной BB′ и сложите ее пополам.

в. Закрепите один конец сложенной веревки в точке F и натяните ее вдоль ряда так, чтобы другой ее конец оказался в точке F₁.

г. Вычертив дугу третьей веревкой от точки C, получите расстояние F₁F₂ тем же способом, каким получали Y₁Y₂. Отрезок F₁F₂ и есть то расстояние, которое надо отмерить от левого столба, чтобы найти искомую точку.

Рис. 7.15. Метод экстраполяции с использованием ряда III в Мерривейле

Эта модификация первого метода уменьшает ошибку экстраполяции примерно вчетверо и делает ее ничтожно малой.

Если наблюдатели в Мерривейле действительно пользовались таким методом экстраполяции, он мог сложиться только в результате многих лет терпеливых и нередко обескураживающих наблюдений и проб. Однажды найденные расстояния β и γ имели бы для строителей очень большое значение, и неудивительно, что их сохранили в расположении рядов, словно данные в «памяти» современного компьютера.

Это истолкование использования каменных рядов в Мерривейле критиковалось на том основании, что оно произвольно и уникально. Бесспорно, до тех пор пока не будет найден еще один памятник раннего бронзового века со сходным методом экстраполяции, такая трактовка Мерривейла остается интересной, но недоказанной гипотезой. Для многого еще не найдены объяснения. Например, зачем понадобились два двойных ряда, имеющих как будто одно назначение, и в чем смысл единицы длины а? Вероятно, предложенное толкование верно лишь наполовину, и дальнейшие исследования этих и других каменных рядов в конце концов прольют свет на их смысл.

Региональные варианты метода экстраполяции не должны нас удивлять. Мы видели, что на самом севере Шотландии данные указывают на существование постоянной решетки из камней, служившей счетным устройством для экстраполирования, тогда как на юге Шотландии как будто обходились треугольником с одной стороной, равной 4G. На юге Англии, где существовала традиция строительства каменных рядов, мы вновь находим указания на постоянные каменные системы, облегчающие расчеты. Хотя нас может удивлять, каким образом их умудрились создать в раннем бронзовом веке, во всяком случае пользование такими счетными устройствами было несложным — после того как их сооружение было закончено. Каменные ряды Бретани, которые я опишу в следующей главе, воплощают еще один вариант этих основных идей. Именно там наблюдение и истолкование астрономических явлений достигло наибольшей сложности и тщательности среди всех культур раннего бронзового века на северо-западе Европы.