Градусы скорости

Учение об «интенсификации и ремиссии качеств» или, как его еще называли, «de latitudinibus formarum» (о «широте форм») было развито в XIV—XVI вв. схоластами Мертон-колледжа в Оксфорде¹ (в арифметико-алгебраической форме par excellence), Парижского университета² (преимущественно в геометрической форме), а также в Италии³. Область применения этого учения, цель которого состояла в математизации представлений об интенсивности качеств и её изменении, была чрезвычайно широка — от математического описания интенсивностей теплоты, света и скорости до обсуждения интенсивности благодати, греха, милосердия и добродетельности. Далее я сосредоточусь на приложении подходов указанных авторов к проблемам кинематики.

Понимание «локального движения» как перемещения тела, при котором оно «было в одном месте и будет в другом, причем так, что ни в один момент оно не покоится ни в одной точке» можно встретить уже в сочинениях Уильяма Оккама (W. Ockham, ок. 1285 — ок. 1350)⁴, хотя последний полагал, что в абсолютном смысле, т. е. логически, никакого движения нет вообще. Брадвардина, не разделявшего оккамистского взгляда на движение, интересовало прежде всего соотношение скоростей движущихся тел, а также соотношение между скоростью, движущей силой и сопротивлением среды. Исследовать движение, по его мнению, значит изучать изменение отношений скоростей в зависимости от изменения отношения между силой и сопротивлением. Свой закон движения Брадвардин формулирует следующим образом: «отношения движущих сил к силам сопротивления пропорциональны скоростям движения, и наоборот»⁵.

У Брадвардина, по словам В.П. Зубова, «сложилось понятие о скорости как о некой отвлеченной величине (т. е. отношении), в определение которой не входит ни понятие времени, ни понятие пути»⁶. «Количество движения (quantitas motus)», по Брадвардину, определяется его продолжительностью. Понятие скорости, отвлеченное от непосредственно пространственных определений, позволяло преодолеть аристотелевское разделение движений по их траекториям (прямолинейное (вниз-вверх) и равномерное круговое), поскольку «понятие траектории как результата независимых движений позволяло сопоставлять и сравнивать движения различной формы»⁷. Скорость понималась Брадвардином как «качество движения (qualitas motus)», а потому ей, как и каждому качеству, присуща некоторая интенсивность, причем можно говорить об интенсивности скорости в каждый данный момент времени, т. е. о velocitas instantenea (мгновенной скорости). По Хейтесбери, мгновенная скорость при неравномерном движении определяется «не по пройденному отрезку, а по линии, которую прочертит подобная точка, если бы она стала двигаться униформно в течение такого-то или иного времени, или проходить такой-то путь с тем градусом скорости, с которым она движется в данное мгновение»⁸.

Понимание мгновенной скорости как своеобразного «внутреннего качества <...>, определенного в каждый момент движения»⁹ создало предпосылки полного преобразования в будущем всей теории движения, поскольку способствовало формированию инфинитезимальной трактовки движения.

В связи со сказанным следует особо остановиться на концепции «конфигурации качеств и движений», развитой Н. Оремом и его последователями, поскольку именно эта концепция оказала наиболее глубокое влияние на Галилея, когда он обращался к изучению свободного падения, хотя вопрос о «влияниях» и «предтечах» весьма непрост и дискутируется в литературе уже не один десяток лет.

Доктрина конфигурации качеств была сформирована для описания и геометрического представления интенсивности качеств. «Всякая вещь, поддающаяся измерению, — писал Орем, — за исключением чисел, воображается в виде непрерывной величины. Следовательно, для ее измерения нужно воображать точки, линии и поверхности, или их свойства <...>. И даже если неделимые точки или линии — ничто, тем не менее, нужно их математически вымыслить для познания мер вещей и их отношений»¹⁰.

Интенсивность качества выражалась его степенями (или градусами). Орем предложил представлять отношение интенсивностей отношением отрезков прямых, поскольку именно в линии он находит «всё, что существенно связано с понятием интенсивности, — соизмеримость (или несоизмеримость), континуальность, возможность бесконечного роста и убывания»¹¹.

Каждый предмет (subjectum) Орем представляет горизонтальной линией или плоскостью (longitudo или extenso)¹², тогда как степень интенсивности качества изображается перпендикулярными отрезками (перпендикулярность отрезков здесь не принципиальна, это вопрос удобства) — latitudo, intensio, gradus, — исходящими из точек линии (или поверхности), характеризующей объект. Тогда отношение между двумя «точечными» интенсивностями мыслится как отношение между двумя перпендикулярными отрезками прямой. По словам Якопо де Санто Мартино, комментатора Орема и автора популярного учебника «De latitudinibus formatorum» (1-е изд. — Падуя, 1486), «столько же, сколько точек имеется в линии, столько же линий будет и в плоскости, — линий, восстановленных перпендикулярно из каждой её точки. Пропорционально величине этих линий мы должны представлять себе большую или меньшую интенсивность формы в этой точке, — в соответствии с тем, насколько длиннее или короче по сравнению с другими перпендикулярная линия, измеряющая высоту плоскости в этой точке»¹³.

Рис. 17. Диаграмма Н. Орема для случая «униформного» распределения качества по «долготе»

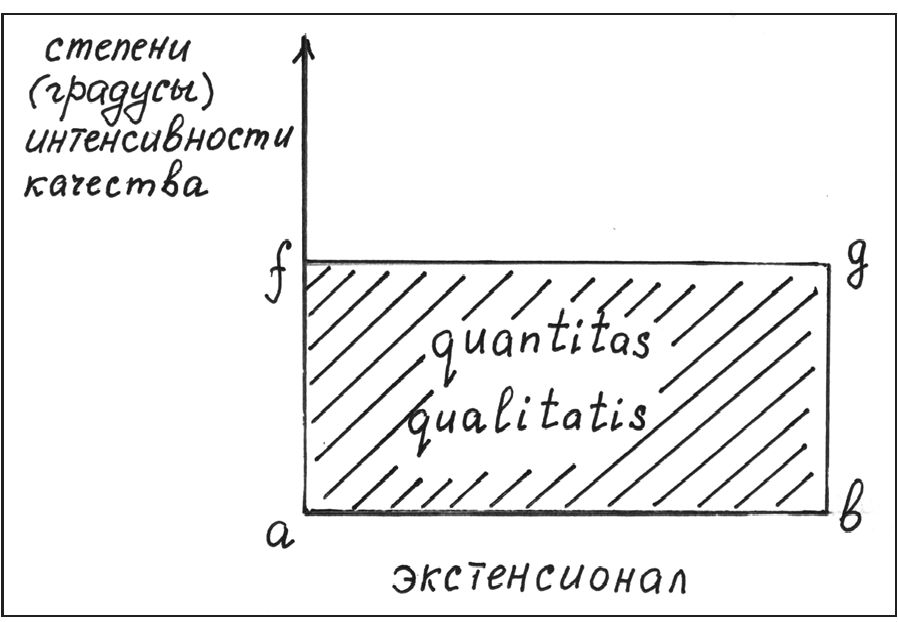
Отношение линий (отрезков) интенсивности, таким образом, выражало отношение между самими интенсивностями качества в разных точках объекта (или в разных «точках» его экстенсивной характеристики), а вся поверхность, образуемая «широтными» линиями, составляла «конфигурацию качества».

Если рассматривалось движение тела, то в качестве longitudo выступал пройденный путь или время, а в качестве latitudo — «градусы скорости», т. е. мгновенные скорости, в разных точках пути или в разные моменты времени. В случае, когда объект представлен линией, во всех точках которой интенсивность его некоего качества одинакова (т. е. имеет место «униформное» распределение качества по «долготе», примером может служить равномерное прямолинейное движение), получаемая поверхность представляет полное quantitas qualitatis (полное количество качества) и имеет прямоугольную форму (рис. 17). Если же разным «долготным» точкам отвечают различные интенсивности, то получаемая поверхность (точнее, ограничивающая ее сверху linea summitatis, соединяющая вершины всех «широтных» отрезков) может иметь самую разнообразную форму, и в этом случае качество называлось дифформным (например — дифформное (неравномерное) движение).

Рис. 18. Диаграмма Н. Орема для случая «униформного-дифформного» распределения качества по «долготе»

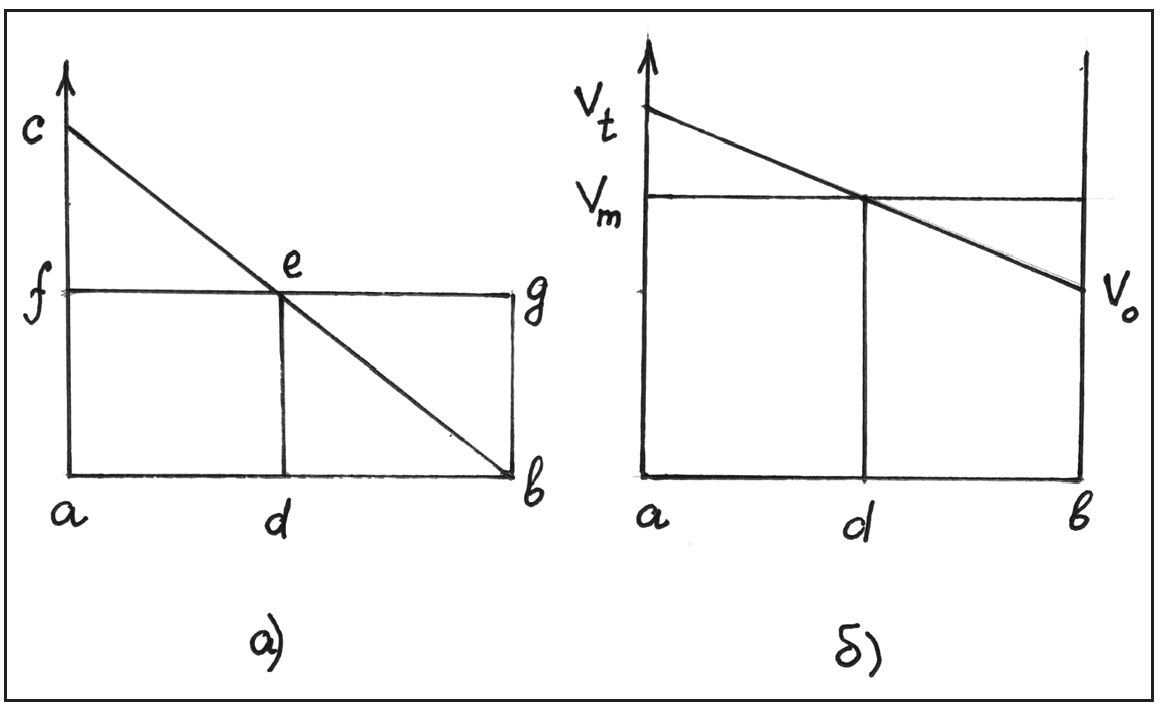
Важным частным случаем был случай так называемого униформно-дифформного распределения качества по экстенсионалу (долготе), когда интенсивность его менялась прямо пропорционально (линейно) долготе. Тогда quantitas qualitatis изображалось прямоугольным треугольником (рис. 18) или трапецией.

Заметим, что площадь получаемой геометрической фигуры (прямоугольника, треугольника и т. д.) характеризует, в случае рассмотрения движения тел, общее количество скорости, так называемую velocitas totalis (суммарную скорость), и если экстенсионалом выбрано время движения, то площадь соответствующей фигуры будет характеризовать пройденный за время движения путь. По замечанию В.П. Зубова, «Орем нигде прямо не говорит [об этом], но подразумевает» такой вывод¹⁴.

В нашем контексте важно упомянуть так называемое правило Орема или, другое название, Merton Rule (Merton Theorem)¹⁵: «Всякое качество, если оно униформно-дифформно, по своей величине таково, каким было бы униформное качество того же или равного ему предмета, соответствующее градусу средней точки того же предмета. При этом имеется в виду случай, когда качество линейное»¹⁶.

В применении к случаю униформно-дифформного, т. е. равноускоренного, движения это означает, что за время t тело, движущееся прямолинейно и равноускоренно, так, что его скорость в конце пути будет равна V_max, пройдет то же расстояние, какое за это же время преодолеет тело, движущееся равномерно и прямолинейно с постоянной скоростью V = V_max/2¹⁷. На языке диаграмм Орема этот вывод интерпретируется как равенство площадей abc и прямоугольника afgb (рис. 19) при условии, что af = fc и ad = db¹⁸.

Рис. 19. Графическое представление Merton Rule в его общей формулировке (а) и применительно к случаю соотношения прямолинейного равноускоренного и прямолинейного равномерного движений (б)

В трактате Questiones super geometriam Euclidis Орем выводит из указанного правила важный для кинематики равноускоренного движения результат: в случае такого движения «отношение общего качества (qualitatis totius) к качеству части, оканчивающейся нулевой степенью, есть двойное отношение всего предмета к этой части предмета <...>. И мы должны говорить в этом случае о качестве поверхности по отношению к его предмету и о скоростях движения по отношению ко времени»¹⁹. Если переформулировать сказанное применительно к скоростям движения, то суммарная скорость (quantitas velocitatis totalis)²⁰, выраженная горизонтальным («долготным») отрезком на диаграмме Орема, будет пропорциональна квадрату времени (s ~ t²).

Другая важная особенность теории конфигурации качеств и движений упоминается в замечании Орема о том, что «неделимая точка не есть что-либо реальное, ни линия, ни поверхность, хотя воображение их пригодно для лучшего постижения меры вещей»²¹. По мнению А.В. Ахутина, «именно такое понимание математического будет характерно впоследствии для физиков XVII в. и, в частности, для Галилея»²². Я бы выразился осторожней. Да, конечно, в трудах мертонских калькуляторов и парижских номиналистов XIV столетия действительно заложено многое, что затем стало мыслительным материалом для науки и философии Нового времени. Однако, как будет показано далее, галилеево понимание инфинитезимальной структуры континуума много сложней и противоречивей, чем у его предшественников-схоластов.

Мгновенная скорость в трудах Галилея — это некая промежуточная конструкция, одновременно и физическая, и математическая. Если Орем настаивал на необходимости «вымыслить» неделимые точки и линии, которое сами по себе есть ничто²³, то Галилей, вводя понятие актуальной бесконечности, обосновывает математичность физической природы существованием подобных двойственных, пограничных объектов типа геометро-физических атомов и мгновения, которое есть одновременно время и не-время. Одно дело допускать, что геометрические формы могут служить универсальным репрезентантом «конфигурации качеств» и тем самым быть полезными для истолкования реальных характеристик предметов, и совсем другое — настаивать на том, что Книга Природы написана на языке математики, понимая это утверждение не в смысле Платона (для которого математические конструкции — это объекты мира идей), но буквально: Природа состоит из математических форм и потому явления полностью определены математически. Оремова «конфигурация», и здесь я полностью согласен с А.В. Ахутиным, воспринимается как свидетельство о реальной сущности, а не осмысливается в качестве этой сущности, «эссенции» предметов. «Символическое отношение исключает возможность той взаимопреобразующей связи между реальным и идеальным, которая характерна для экспериментально-теоретической ситуации физики Нового времени. Истолковывающий же эксперимент Средневековья всегда связан с тем или иным символическим отношением. Результаты идеализаций, схематические изображения, формулы истолковываются либо как "реалистические" свидетельства, либо как определение "языка"»²⁴.

Однако глубинное различие в подходах Орема²⁵ и Галилея к принципам теоретического осмысления природы движения не стало препятствием для перенимания и трансформации приема геометрического или арифметико-алгебраического описания движения, приема, который у Галилея оказался включенным в иной, неперипатетический натурфилософский контекст, а кроме того, стал не просто абстрактно-символическим репрезентантом движения, но расчетным инструментом.

Примечания

1. Так называемыми «мертонскими калькуляторами»: У. Хейтсбери (W. Heytesbury или Hentisberus, ум. в 1380), Р. Суайнсхедом или Суиссетом (R. Swineshead или Suisheth; ум. после 1355), Д. Дамблтоном (John of Dumbleton; умерок. 1349) и другими учениками и последователями Т. Брадвардина (Th. Bradwardine; ок. 1290—1349).

2. Николаем Оремом (N. Oresme.; ум. в 1382), Альбертом Саксонским (Albertus de Saxonia; ум. в 1390 г.), Марсилием Ингенским (Marsilius von Inghen; ум. в 1396) и другими представителями так называемой «школы Жана Буридана».

3. Дж. Казале из Монферрато (Joannes de Casali; XIV в.), Бьяджо Пелакани или Пеликани (лат. Blasius de Parma, B. Pelacani или Pelicani da Parma; ок. 13451416), Гаэтано Тиенским (Gaetano da Thiene; 1387—1465) и др. Подр. см.: Григорьян А.Т., Зубов В.П. Очерки... С. 122—143.

4. Ockham W. Philosophical Writing / A selections edited and translated by Philotheus Boehner. Edinburgh: Nelson, 1957 (Series: Nelson Philosophical Texts). P. 140.

5. Цит. по: Ахутин А.В. История принципов... С. 132.

6. Григорьян А.Т., Зубов В.П. Очерки... С. 66.

7. Ахутин А.В. История принципов... С. 133—134.

8. Цит. по: Григорьян А.Т., Зубов В.П. Очерки... С. 69.

9. Ахутин А.В. История принципов... С. 133.

10. Орем Н. О конфигурации качеств / Предисл., пер. и примеч. В.П. Зубова. М.: Эдиториал УРСС, 2000. С. 40—123; С. 41.

11. Ахутин А.В. История принципов... С. 137. «И так как величина или отношение линий более понятны и легче постигаются нами, — разъяснял свой подход Орем, — а кроме того, линия занимает первое место среди видов континуума, то подобная интенсификация (intensio) должна быть воображаема в виде таких линий, которые примыкают к предмету и поставлены отвесно к нему» (Орем Н. О конфигурации... С. 42).

12. При этом экстенсивность объекта могла иметь как пространственное определение, так и временное, т. е. характеризовать время, в течение которого наличествует данное качество, скажем, продолжительность движения.

13. Цит. по: Григорьян А.Т., Зубов В.П. Очерки... С. 129.

14. Григорьян А.Т., Зубов В.П. Очерки... С. 133.

15. Damerow P., Freudentahl G., Mc Laughlin P., Renn J. Exploring the Limits... P. 17.

16. Орем Н. О конфигурации... С. 110.

17. Для современного читателя этот результат тривиален: V_равном = s/t = at²/2t = at/2 = V_max/2, где a — ускорение.

18. Действительно, 1/2(V₀+V_t)t = V_mt, где V_m — средняя скорость.

19. Nicole Oresme and the medieval geometry of qualities and motions; a treatise on the uniformity and difformity of intensities known as Tractatus de configurationibus qualitatum et motuum / Edited with an introduction, English translation, and commentary by Marshall Clagett. Madison: University of Wisconsin Press, 1968. P. 557—559.

20. Т. е. путь, пройденный за время t.

21. Орем Н. О конфигурации... С. 107.

22. Ахутин А.В. История принципов... С. 143.

23. Свой подход Орем описывает лишь как «способ представления (imaginatio)», предупреждая, что «все это говорится не в физическом смысле» (Орем Н. О конфигурации... С. 107).

24. Ахутин А.В. История принципов... С. 142.

25. Здесь Орем — это скорее имя-символ всей калькуляторской традиции.