Ложным путем к истине

Как уже было сказано, Галилей использовал понятие конфигурации качеств и диаграммы Орема при рассмотрении ускоренных и замедленных движений. В некоторых документах, датируемых приблизительно 1604 г.¹, он детально анализирует то «твердое начало», о котором упоминается в цитированном выше фрагменте его письма П. Сарпи.

Обратимся в качестве примера к документу MS, fol. 128, в котором ход рассуждений Галилея представлен наиболее полно.

Рис. 20. Диаграмма из рукописи Галилея MS, fol. 128

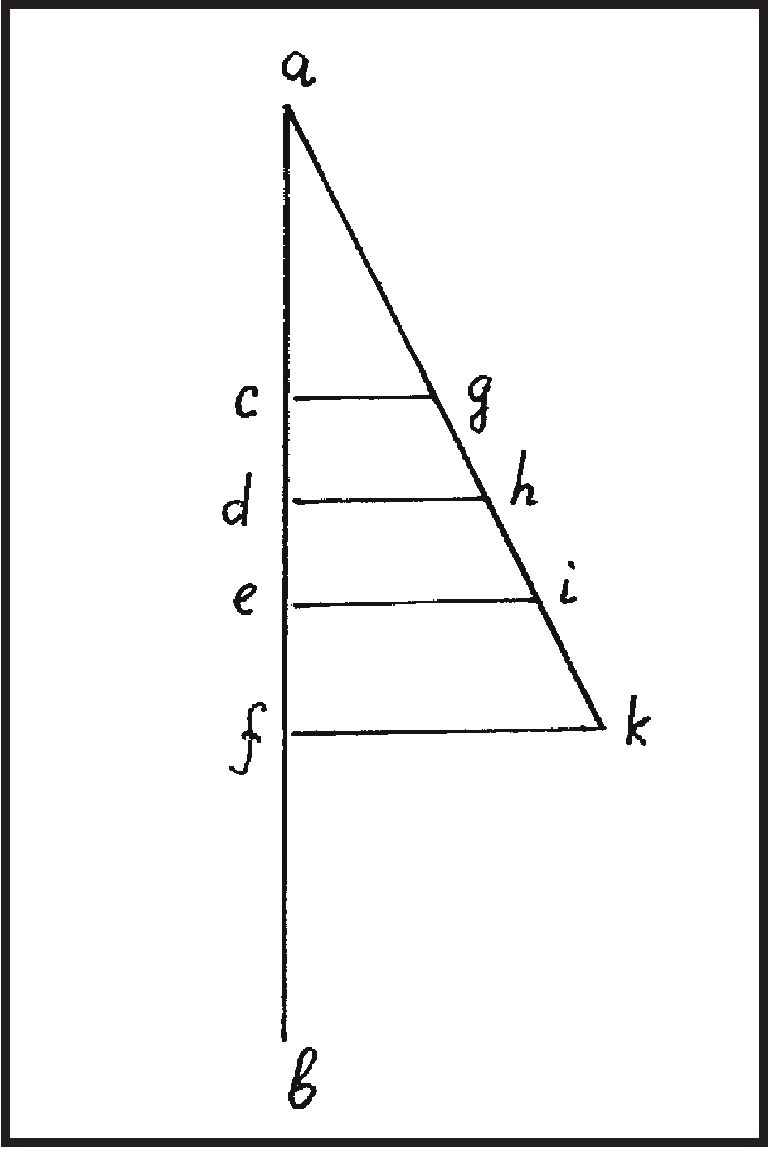
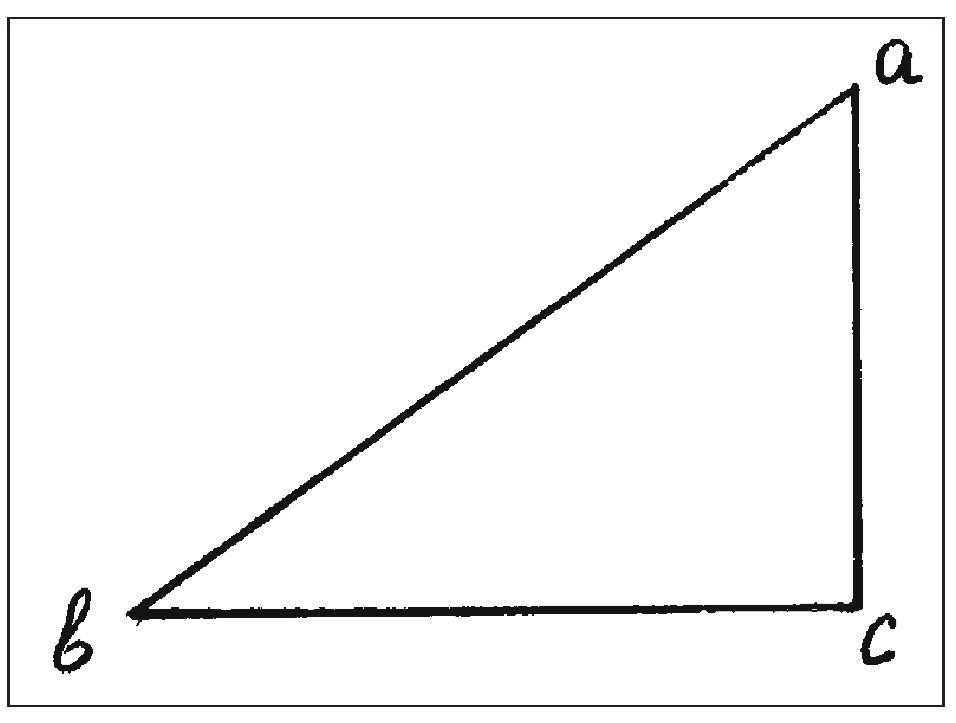
«Я предполагаю, — пишет Галилей, — и возможно, смогу доказать, что естественно падающее тяжелое тело непрерывно увеличивает свою скорость по мере увеличения расстояния от точки начала движения, как, например, тяжелое тело, начавшее двигаться из точки a (рис. 20) и падающее вдоль линии ab. Я предполагаю, что степень скорости в точке d настолько превышает степень скорости в точке c, насколько расстояние da больше, чем ca, а степень скорости в [точке] e относится к степени скорости в [точке] d как ea [относится] к da. Таким образом, в каждой точке линии ab тело должно иметь степень скорости, пропорциональную расстоянию этой точки от начальной точки [движения] a. Этот принцип представляется мне весьма естественным и соответствующим всем нашим наблюдениям над инструментами и машинами, работающими посредством удара, где ударяющий предмет производит тем больший эффект, чем с большей высоты он падает; и этот принцип я докажу далее».

Итак, основной принцип, положенный Галилеем в основание его теории естественного ускоренного движения, фактически сводится к тому, что скорость такого движения есть непрерывная линейная функция пройденного пути, т. е. V = kS. Теперь продолжим цитирование и посмотрим, к каким выводам приходит Галилей и как он доказывает сформулированный принцип.

«Начертим линию ak под произвольным углом к линии af (см. рис. 20. — И.Д.) и через точки c, d, e и f проведем параллельно линии cg, dh, ei и fk Так как отрезки fk, ei, dh и cg относятся друг к другу как fa, ea, da и ca, то скорости в точках f, e, d и с относятся друг к другу как отрезки fk, ei, dh и cg. Таким образом, степени скорости нарастают непрерывно в точках линии af по мере увеличения длины параллельных отрезков, проведенных из всех этих точек. Более того, поскольку скорость, с которой движущееся тело перемещается из точки a в точку d, слагается из всех степеней скорости, кои тело проходит во всех точках отрезка ad, а скорость, с которой тело проходит отрезок ac, слагается из всех степеней скорости, которые оно имело во всех точках отрезка ac, то скорость прохождения телом отрезка ad также находится в том же отношении к скорости, с коей тело проходит отрезок ac, какое все параллельные линии, проведенные из всех точек отрезка ad ко всем точкам отрезка ah, имеют ко всем параллельным линиям, проведенным из всех точек ac ко всем точкам ag, и это отношение есть отношение [площади] треугольника adh к треугольнику acg (т. е. к площади этого треугольника. — И.Д.), т. е. отношение квадрата [стороны] ad к квадрату [стороны] ac. Таким образом, скорость, с которой оно проходит отрезок ad, так относится к скорости, с которой оно проходит отрезок ac, как квадрат da к квадрату ca.

А поскольку одна скорость относится к другой скорости обратно тому, как время одного движения ко времени другого (ибо увеличить скорость — это всё равно что уменьшить время), то время движения по ad относится ко времени движения по ac как квадратные корни расстояний ad и ac. Таким образом, расстояния, проходимые из начальной точки движения, относятся друг к другу как квадраты времен и dividendo² пути, проходимые в равные времена, соответствуют последовательности нечетных чисел, начиная с единицы. Это соответствует как тому, что я уже сказал, так и наблюдениям; и, таким образом, все истины находятся в согласии»³.

Приведенное рассуждение, во-первых, совершенно ошибочно (кроме окончательного вывода), причем ошибочно вдвойне: скорость равноускоренного движения не является линейной функцией пройденного пути и, кроме того, отношение (средних) скоростей не равно отношению квадратов пройденных путей, т. е., если уж допускать, что V = ks и, следовательно, V₁/V₂ = s₁/s₂, то отсюда вытекает, что отношение площадей соответствующих треугольников S₁ = 1/2(V₁s₁) и S₂ = 1/2(V₂s₂), и равно S₁/S₂ = V₁s₁/V₂s₂ = s₁²/s₂² = V₁²/V₂², а вовсе не S₁/S₂ = s₁²/s₂² = V₁/V₂. Галилей сначала предполагает, что V ~ S, а потом, на основании этого предположения, «доказывает», что V ~ s². И из всего сказанного им уж никак не получается, что времена относятся как квадратные корни из величин пройденных путей.

Во-вторых, всё это многословное рассуждение по большей части обладает признаками не доказательства, но геометрической иллюстрации исходного тезиса.

Таким образом, Галилей формулирует верный вывод — правило нечетных чисел — исходя из совершенно неверной посылки и ошибочных рассуждений⁴.

Следующий шаг в галилеевых исследованиях равноускоренных движений зафиксирован в документе MS, fol. 163v⁵, примыкающем по своему характеру к перечисленным выше записям (MS, fol. 179v, 85v и 128). В этом документе Галилей формулирует правило, которое в историконаучной литературе иногда называют Double Distance Rule (правило двойного пути; далее сокр. ПДП)⁶:

Рис. 21. Графическая иллюстрация Галилея к выводу правила двойного пути

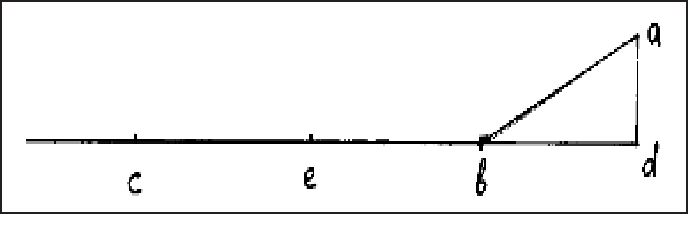
«Пусть движение [происходит] из точки a в точку b с естественным ускорением (речь идет о свободном падении тела. — И.Д.). Я утверждаю, что, если скорость во всех точках отрезка ab была бы такой же, как в точке b, то [тело] прошло бы этот путь ab в два раза быстрее».

Из этого совершенно правильного утверждения (доказательство которого, приведенное Галилеем, я опускаю), следует, что, если тело движется равноускоренно по наклонной плоскости ab (рис. 21), а затем равномерно по горизонтальному отрезку пути bc вдвое большему ab (bc = 2ab), то расстояния bc и ab оно должно преодолеть за равные промежутки времени. Сказанное составляет суть ПДП, тогда как первое утверждение в приведенной выше цитате является, по существу, упомянутым выше мертонским правилом (Merton Rule). Как и в предыдущем случае (документ MS, fol. 128), Галилей получает правильные результаты, исходя из ошибочного предположения (V = ks). Полезность ПДП определялась тем, что с его помощью можно было заменять в рассуждениях и доказательствах ускоренное движение равномерным.

Итак, к октябрю 1604 г., т. е. к моменту написания письма Сарпи, Галилей пришел если не к законченной теории, то, по крайней мере, к совокупности идей и предположений, касающихся равноускоренного движения (свободного падения и движения по наклонной плоскости):

— V = ks
— s ~ и имеет место ПНЧ;
— lt-отношение
— ПДП.

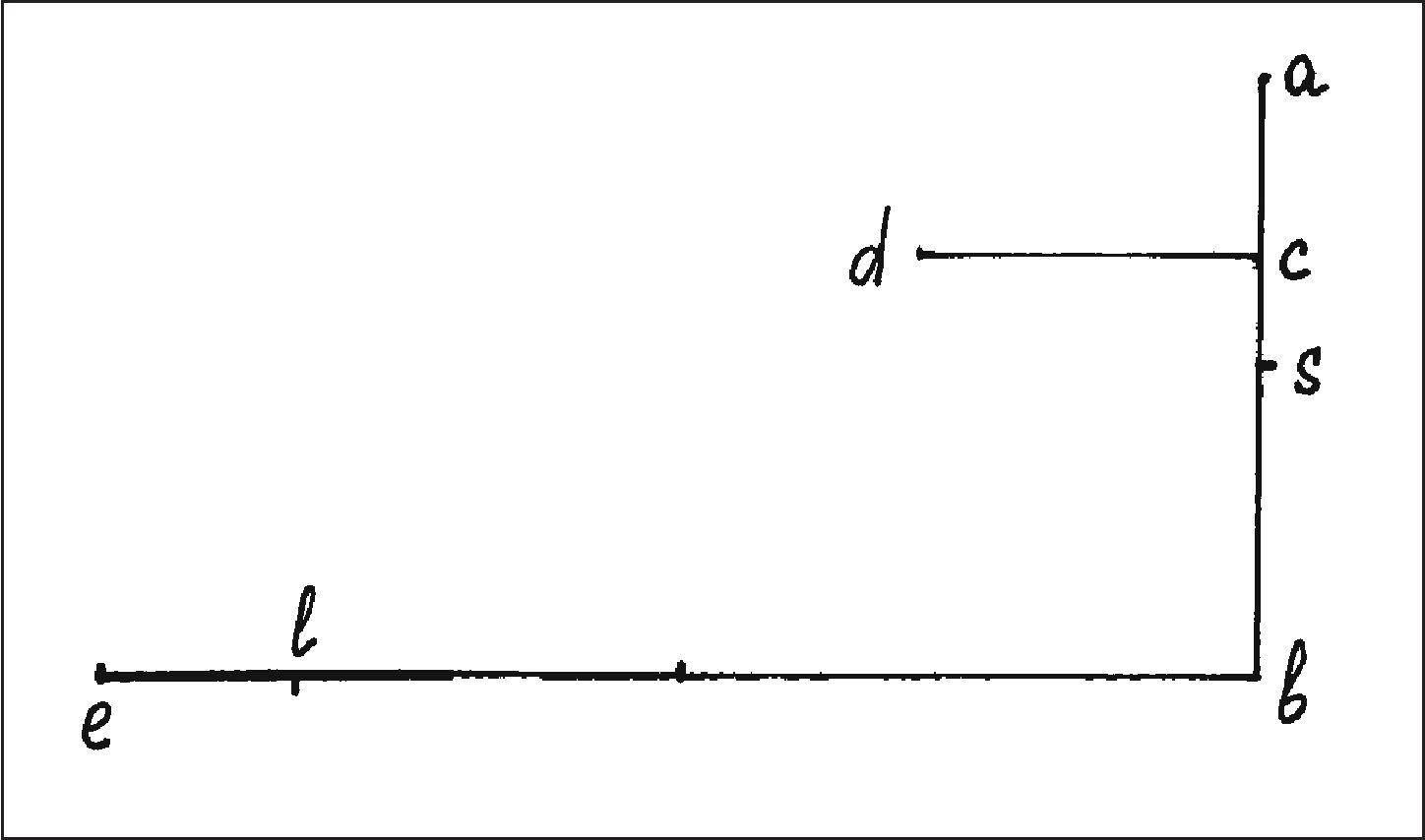
Кроме того, он использовал диаграммы Орема, которые в его рассуждениях стали расчетным инструментом, протоинфинитезимальные представления (понятие мгновенной скорости, velocitas totalis и т. п.)⁷ и также некоторые результаты, полученные еще в XIV столетии.

В письме Б. Винта от 7 мая 1610 г., накануне своего переезда из Падуи во Флоренцию, Галлей сообщал: «среди работ, которые мне предстоит завершить, две книги «De Systemate seu constitutione», в которых затрагиваются всеобщие проблемы философии, астрономии и геометрии; три книги о движении тел — это совсем новая концепция, не имеющая ничего общего ни с прежними, ни с современными теориями»⁸.

Действительно, хотя к этому времени Галилея больше интересовали астрономические проблемы, однако и до 1610 г., и после он время от времени возвращался к вопросам механики, особенно когда «было благоразумнее заняться предметами, не имеющими явных идеологических импликаций»⁹. Среди документов падуанского периода в контексте рассматриваемой темы особого внимания заслуживают рукописные заметки MS, fol. 91v¹⁰ и MS, fol. 152r¹¹. Далее я сосредоточусь на первом из этих документов, в котором изменение взглядов Галилея на природу равноускоренного движения отражено с наибольшей полнотой¹². В этих заметках Галилей приводит доказательство следующего утверждения: «При движении из состояния покоя момент скорости и время движения растут в одном и том же отношении». Это важная констатация, поскольку она свидетельствует о том, что Галилей, наконец, оставил прежнюю гипотезу (V = ks) и обратился к новой: V = V(t). «Пусть, — читаем далее, — движение происходит по ab из состояния покоя в точке a и пусть c — произвольная точка на ab, и пусть эта точка располагается так, что ac есть время падения по ac и пусть b — произвольная точка (рис. 22): я утверждаю, что время падения вдоль ab так относится ко времени [падения] вдоль ac, как момент скорости в [точке] b к моменту [скорости] в [точке] c»¹³.

Рис. 22. Диаграмма Галилея к доказательству закона равноускоренного движения (V ~ t).

Суть предложенного Галилеем доказательства того, что V ~ t такова. Рассмотрим падение тела вдоль линии ab. Отложим из точки c на ab отрезок cd = 2ac и перпендикулярный ab. Из точки b отложим отрезок be = 2ab, также перпендикулярный ab. Тогда:

cd/be = ac/ab.

В соответствии с ПДП имеем: cd = t_acV^c, где V^c — скорость тела, достигнутая им за время падения t_ac в точке c; be = t_abV^b, где V^b — скорость тела, достигнутая им за время t_ab в точке b. Пусть bl — отрезок, который тело прошло бы, двигаясь равномерно по горизонтали со скоростью V^b, но за меньшее время t_ac, т. е. bl = t_acV^b.

Кроме того, согласно (2), можем записать:

t_ab/t_ac = ab/(√(ab·ac)) и ab/as = as/ac (3)

или as = √(ab·ac)

Тогда поскольку

cd/bl = V^c/V^b

и учитывая, что

be/bl = (t_ab·V^b)/(t_ac·V^b) = t_ab/t_ac = ab/√(ab·ac) = ab/as = as/ac,

получаем:

V^c/V^b = cd/bl = (cd/be)·(be/bl) = (ac/ab)·(ab/as) = ac/as = t_ac/t_ab

и V^c/V^b = t_ac/t_ab

или V ~ t, что и требовалось доказать.

Таким образом, приведенное доказательство опиралось на ПДП и закон свободного падения (s ~ t²) (он здесь учтен в формуле (3)), который Галилей, в свою очередь, вывел из доказанной в «De Motu» теоремы об «изохронности хорд» и постулированного, но не доказанного lt-отношения (плюс ошибочный вывод этого закона в MS, fol. 128). Однако и ПАП, и закон свободного падения опирались в конечном счете на неверное допущение: V = ks.

В итоге сложилась следующая ситуация: исходя из ошибочного принципа (V = ks) и недоказанного lt-отношения, Галилеем было получено несколько правильных результатов (s ~ t², ПНЧ, ПАП), из которых, в свою очередь, следовало, что исходный принцип неверен и его следует, по-видимому, заменить другим: V = kt. А поскольку Галилей не сразу осознал ошибочность (V ~ s)-допущения, то для него парадоксальность ситуации состояла в том, что из двух несовместимых утверждений следовали одни и те же (как ему казалось) выводы, совместимые, однако, с опытом.

Возможно и другое понимание событий: как свидетельствуют записи MS, fol. 152r, Галилей мог убедиться, что (V ~ s) — допущение несовместимо с ПАП. Но в любом случае необходимо было еще доказать, что из (V ~ t) следует (s ~ t²), и наоборот, причем сделать это надо было, опираясь на теорию пропорций и избегая обращения к диаграммам Орема, Merton Rule, соотнесения velocitas totalis с площадями геометрических фигур и прочего арсенала XIV столетия. Впрочем, уже в приведенном доказательстве диаграмма, изображенная на рис. 21, представляет не символическую репрезентацию отношений экстенсионала и интенсионала, но комбинацию вполне реальных движений, поскольку и вертикальные, и горизонтальные отрезки характеризуют конкретные траектории, проходимые телом.

Рис. 23. Графическое представление свободного падения в «координатах» V — s при допущении, что V = V(t)

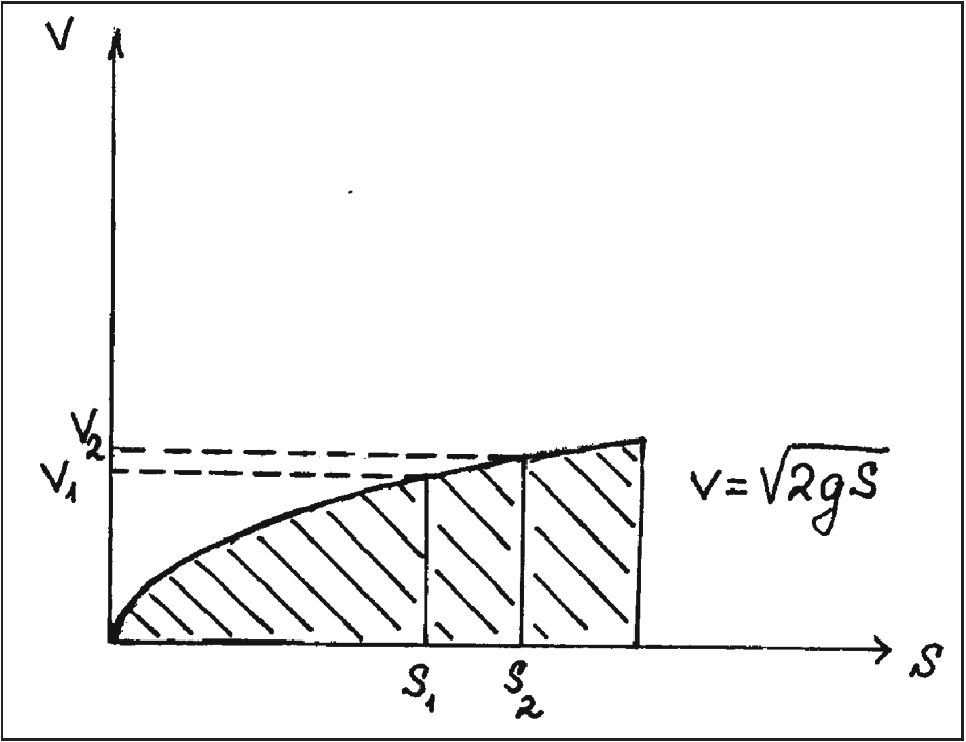
А почему вдруг Галилей решил отказаться от оккамова наследия?

Ответ на этот вопрос дает анализ документа MS, fol. 152r. Галилей фактически рассматривал два способа графического представления равноускоренного движения. Несколько модернизируя его рассуждения (для удобства понимания их современным читателем), можно сказать, что первый способ графического представления свободного падения предполагал его рассмотрение в «координатах» V — s при допущении, что V = V(t). Тогда получаемая им геометрическая фигура была ограничена сверху параболой (рис. 23). Вертикальные отрезки, проведенные к точкам s₁ и s₂, характеризуют моменты (градусы) скорости в соответствующих точках пути.

Рис. 24. Графическое представление свободного падения в «координатах» V — t при допущении V = V(t)

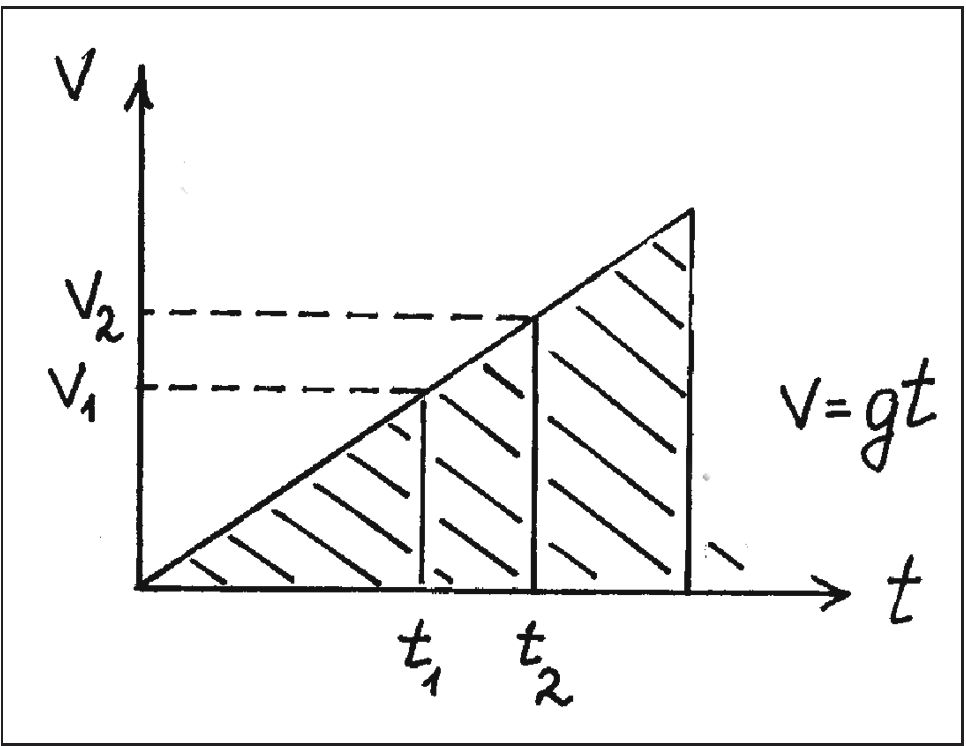
Второй способ графического представления свободного падения — это представление его в «координатах» V — t (если полагать, что V = V(t)). Тогда «конфигурация качеств» будет представлена треугольником (рис. 24). Вертикальные отрезки, проведенные к точкам t₁ и t₂, характеризуют в этом случае моменты (градусы) скорости в моменты времени t₁ и t₂, отвечающие прохождению телом соответственно точек s₁ и s₂.

Рис. 25. Графическое представление свободного падения в «координатах» V — s при допущении V = ks

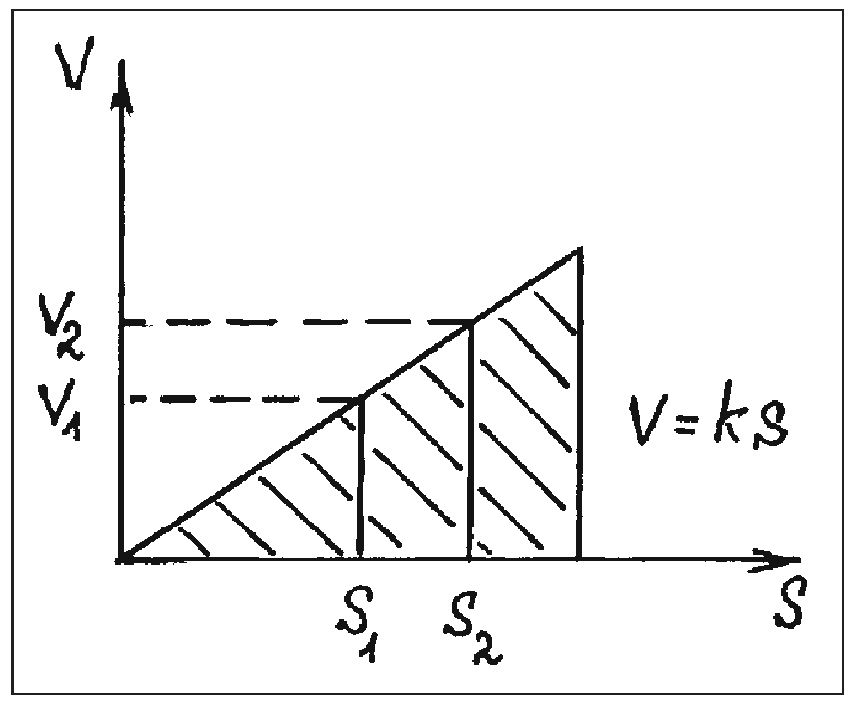
Галилей полагал, что и в том, и в другом случае суммирование всех градусов скорости должно дать одно и то же значение velocitas totalis, характеризуемое величиной заштрихованной площади на рис. 23 и 24. Более того, поскольку, по его ошибочному мнению, оба закона скорости — V = V(s) и V = V(t) — давали один и тот же закон свободного падения (s ~ t²), то и velocitas totalis, полученная суммированием отрезков на диаграмме, построенной в «координатах» V — s в предположении, что V = ks (рис. 25), также должна быть равна тому же значению суммарной скорости.

Или, иначе, во всех трех случаях (V = √(2gs), V = gt и V = ks) отношение площадей S₁ и S₂, отвечающих соответствующим точкам на оси экстенсионала, — s₁ и s₂ или t₁ и t₂ — должно быть одинаковым. Современному читателю ясно, что такого быть не может. Действительно, в первом случае получаем S₁/S₂ = s₁^3/2/s₂^3/2, т.к. S = ∫Vds = ∫√(2gs)ds = √(8g/9)s^3/2,

во втором — отношение площадей равно

S₁/S₂ = t₁²/t₂² = s₁/s₁,

и в третьем:

S₁/S₂ = s₁²/s₂²

И если, к примеру, s₁ = 9 и s₂ = 4 (я беру цифры Галилея), то отношения площадей оказываются следующими: в первом случае — 27/8, во втором — 9/4 и в третьем — —81/16. У Галилея так все

и получилось¹⁴, но он-то считал, что отношение площадей во всех случаях должно быть одинаковым и, скорее всего, равным 81/16, поскольку во всех трех случаях речь шла, как он ошибочно полагал, об одном и том же отношении одних и тех же величин velocitas totalis. Поэтому-то Галилею и потребовался «независимый» от оремовых диаграмм способ вывода закона свободного падения (или, более общо, закона равноускоренного (естественного) движения: s ~ t²) при том, что Галилей уже начал переосмысливать старый, оремово-калькуляторский символический метод представления конфигурации качеств, приближая диаграммы XIV в. либо к схемам реальных движений, либо к тому, что позже стало называться графиком функции.

Итак, первая задача, вставшая перед Галилеем, состояла в том, чтобы вывести закон s ~ t² из (V ~ t)допущения, не используя графические методы. Такая попытка действительно засвидетельствована в документах MS, fol. 61r—64r¹⁵ и MS, fol. 164v¹⁶.

Схема вывода закона свободного падения, использованная Галилеем, такова: пусть тело, движущееся равноускоренно из состояния покоя, к моменту времени t₁ прошло путь s₁ и достигло скорости V₁, а к моменту t₂ оно прошло путь s₂ и достигло скорости V₂, причем V ~ t, откуда

V₂/V₁ = t₂/t₁ (4)

Введем еще одно движение, на этот раз равномерное и прямолинейное со скоростью V₂. Пусть, далее, тело, равномерно двигаясь с этой скоростью, за время t₁ прошло путь s₃. Тогда, поскольку время первого движения (т. е. равномерно ускоренного до точки s₁) равно времени равномерного, то, по Галилею,

s₃/s₁ = V₂/V₁ (5).

При этом Галилей исходил из так называемого «аристотелева отношения»: при t = t₂(s₁/s₂) = V₁/V₂. Однако это отношение справедливо, если мы соотносим либо два равномерных, либо два равноускоренных (или равнозамедленных) движения. В случае же, рассмотренном Галилеем, когда сравнивается равноускоренное и равномерное движение, совершающееся в течение одинаковых промежутков времени, имеет место иное отношение:

s₃/s₁ = V₂t₁/((V₁t₁)/2) = 2(V₂/V₁).

Но, как будет ясно из дальнейшего, эта ошибка — в физическом плане весьма существенная — не повлияла на окончательный результат.

Далее, из равенства скоростей второго (равномерно ускоренного и продолжающегося до точки s₂) и третьего (равномерного) движений Галилей получает следующее отношение:

s₂/s₃ = t₂/t₁ (6),

опираясь при этом на так называемое «отношение Архимеда»: при равенстве скоростей двух движений (V₁ = V₂) имеет место соотношение.

s₁/s₂ = t₁/t₂

Опять-таки, повторяя mutatis mutandis сказанное выше о пропорции (5), истинное соотношение s₂ к s₃ должно иметь вид:

s₂/s₂ = t₂/(2t₁)

но и эта ошибка на окончательный результат не влияет.

Рис. 26. Пояснительный чертеж Галилея к его рассуждениям о движении по наклонной плоскости

Далее, умножая (5) на (6) и учитывая (4), получаем:

s₃/s₁·s₂/s₃ = s₂/s₁ = V₂/V₁·t₂/t₁ = t₂²/t₁² или s ~ t².

В итоге Галилей, используя опять-таки неверные посылки, получает правильный результат. Однако допущенные ошибки незамедлительно дали о себе знать. Как свидетельствует документ MS, fol. 154v¹⁷, Галилей столкнулся с парадоксом, получившим в литературе название Mirandum Paradox¹⁸. Суть его состоит в следующем. Согласно центральной теореме галилеевой теории движения по наклонной плоскости, изложенной в «De Motu», движение по ab (рис. 26) требует большего времени, чем движение по ac или, иначе, скорость тела, движущегося по наклонной плоскости ab, в точке b (V_b^накл) так относится к скорости тела, падающего по вертикали ac, в точке c (V_c^верт), как ac к ab, т. е. как высота наклонной плоскости к её длине:

V_b^накл/V_c^верт = ac/ab<1, откуда V_b^накл <V_c^верт.

С другой же стороны, поскольку из lt-отношения следует, что

ac/ab = t_ac/t_ab,

то, принимая во внимание упомянутое выше «отношение Архимеда» (если V₁ = V₂, то s₁/s₂ = t₁/t₂, и наоборот), получаем, что V_b^накл = V_c^верт.

Этот парадокс заставил Галилея усомниться в применимости «отношения Архимеда» к случаю равноускоренного движения¹⁹. Но тогда сомнительным оказывался и приведенный выше «независимый» вывод закона s ~ t² и следствий из него.

Таким образом, в 1600-х гг. Галилей, хотя и получил ряд правильных результатов, касавшихся свободного падения (например, (V ~ t) — и (s ~ t²)-зависимости), однако не смог доказать полученные выводы, более того, его теория оказалась весьма неопределенной и противоречивой. Mutatis mutandis сказанное относится и к проблеме движения тела, брошенного под углом к горизонту²⁰. Удалось ли Галилею решить проблему свободного падения в двух его поздних и зрелых работах — в «Dialogo» и в «Discorsi»?

Примечания

1. MS, fol. 179v (Galilei G. Le Opere. Vol. VIII. P. 380); MS, fol. 85v. (Ibid. P. 383) и MS, fol. 128. (Ibid. P. 373—374).

2. Этим термином в теории пропорций обозначалась замена отношения a/b = c/d эквивалентным отношением (a - b)/b = (c - d)/d. — И.Д.

3. Galilei G. Le Opere. Vol. VIII. P. 373—374.

4. Замечу также, что и мертонские калькуляторы, и Н. Орем уже знали о том, что при «униформно-дифформном» (т. е. равноускоренном) движении s ~ t² и имеет место ПНЧ (см.: Григорьян А.Т., Зубов В.П. Очерки... С. 149—151).

5. Galilei G. Le Opere. Vol. VIII. P. 383—384.

6. Wisan W.L. The New Science of Motion... P. 204—207; Damerow P., Freudenthahl G., Mc Laughlin P., Renn J., The Exploring Limits... P. 172—174.

7. Мгновенные скорости у Галилея, как и у представителей калькуляторской традиции, соответствовали непрерывно возрастающим отрезкам прямых, в сумме дающих площадь фигуры (скажем, треугольника).

8. Galilei G. Le Opere. Vol. X. P. 351—352.

9. Damerow P., Freudenthahl G., Mc Laughlin P., Renn J., Exploring the Limits... P. 175.

10. Galilei G. Le Opere. Vol. VIII. P. 280—282, 427.

11. Ibid. P. 426—427.

12. См. также: Damerow P., Freudenthahl G., Mc Laughlin P., Renn J., Exploring the Limits... P. 177—196; Wisan W.L. The New Science... P. 227—229; Naylor R.H. Galileo's Theory of Projectile Motion. P. 550—570; P. 562—566; Wisan W.L. Galileo and the Process of Scientific Creation. P. 269—286; Hill D.K. Galileo's Work on 116v A New Analysis // Isis. 1986. Vol. 77. № 287. P. 283—291; P. 284—288.

13. Galilei G. Le Opere. Vol. VIII. P. 281—282. Курсивом выделен текст, подчеркнутый Галилеем.

14. Площадь под параболой он вычислял, аппроксимируя её треугольниками (см. подр. Damerow P., Freudenthahl G., Mc Laughlin P., Renn J. Exploring the Limits... P. 183—195; P. 189).

15. Mss. Gal., part. VI, Vol. III, fol. 61r-64r, копия рукой Вивиани с оригинала Галилея (Galilei G. Le Opere. Vol. VIII. P. 614).

16. Ibid. P. 375. См.: Wisan W.L. The New Science... P. 201—204.

17. Galilei G. Le Opere. Vol. VIII. P. 375.

18. С. Дрейк перевел термин mirandum как remarkable (Drake S. Galileo at Work... P. 125), а в другой работе как marvelous (Drake S. History of Free Fall... P. 55).

19. Действительно, если при одном и том же ускорении скорости тела в точках b и c оказываются равными, то это означает, что пройденные пути и времена движения равны, что ясно (нам, но не Галилею) из соотношений V = at и V = √(2as).

20. Подр. см.: Damerow P., Freudenthahl G., Mc Laughlin P., Renn J., Exploring the Limits... P. 144—147; 149—153; 200—226.