«De Motu Locali»

Начну с «Discorsi», где изложение вопроса дано в наиболее детальном и систематическом виде. «День третий» этого трактата-диалога начинается с чтения собравшимися сочинения «Академика», т. е. самого Галилея, члена Академии деи Линчеи, «De Motu locali», написанного по-латыни, тогда как сами собеседники говорят между собой по-итальянски. Труд Академика начинается с рассмотрения равномерного движения, которое определяется им как «такое, при котором расстояния, проходимые движущимся телом в любые равные промежутки времени, равны»¹. И далее, после рассмотрения особенностей равномерного движения, автор обращается к движению естественно-ускоренному, формулируя следующую теорему: «Время, в течение которого тело, вышедшее из состояния покоя и движущееся с униформным ускорением (т. е. равномерно ускоренно. — И.Д.), проходит некоторое расстояние, равно времени, в течение которого это же самое расстояние было бы пройдено тем же телом при равномерном движении (motu aequabili), градус скорости которого вдвое меньше высшего и последнего градуса скорости, достигаемого при первом униформно ускоряющемся движении»².

Рис. 27. Пояснительный чертеж Галилея к его рассуждениям о равноускоренном движении (из рукописного трактата De Motu locali)

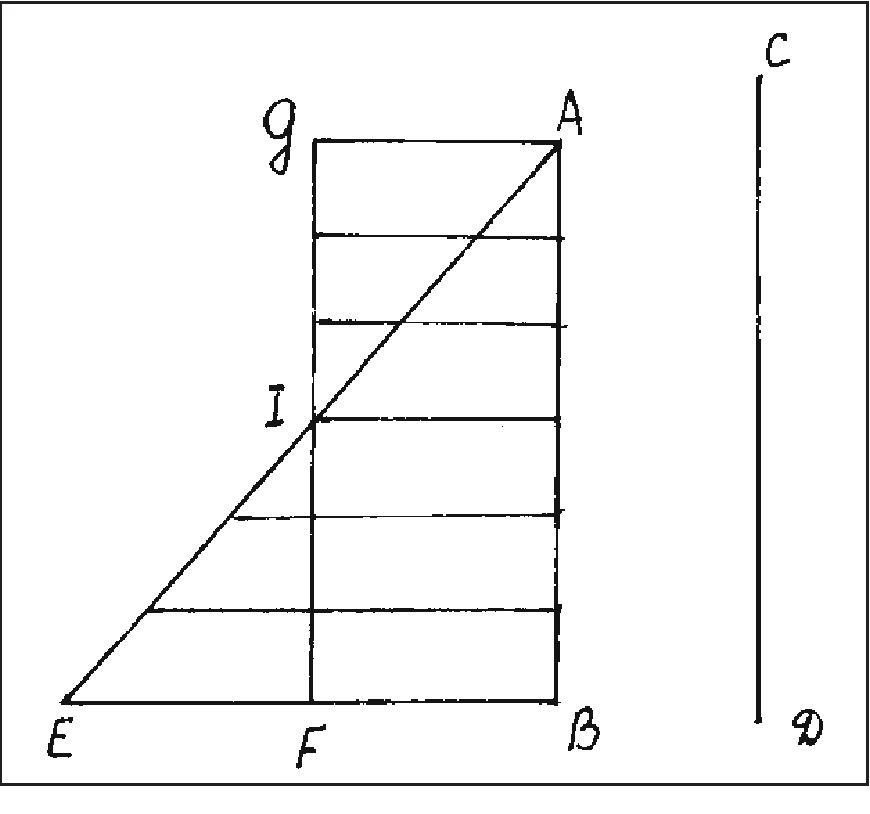
Фактически это утверждение эквивалентно Merton Rule, изложенному, правда, не в терминах средней скорости, а в терминах «высшего и последнего градуса скорости» равноускоренного движения, т. е. фактически повторяющее галилеево ПДП. Теперь обратимся к доказательству этой теоремы, предложенному в «De Motu locali»:

«Пусть линия AB представляет время, в течение которого тело, выйдя из состояния покоя в точке C и двигаясь с униформным ускорением, проходит расстояние CD (рис. 27). Пусть, далее, из градусов скорости, возрастающей в каждое мгновение времени AB, наибольший и последний будет обозначен линией EB, перпендикулярной к AB. Если соединить точки A и Е, то все линии, проведенные из отдельных точек линии AB параллельно EB, будут обозначать возрастающие градусы скорости после мгновения A. Если далее разделить линию EB пополам в точке F и провести линии FG и AG, соответственно параллельные AB и BF, то получится параллелограмм AGFB, равный (прямоугольному. — И.Д.) треугольнику AEB; сторона его GF делит AE пополам в точке I; поэтому если параллельные линии треугольника AEB продолжить до линии IG, то совокупность (aggregatum) всех параллельных линий, заключенных в четырехугольнике, будет равна совокупности линий, заключенных в треугольнике AEB; ведь те, которые заключены в треугольнике IEF, равны тем, которые заключены в треугольнике GIA; а те части, которые заключены в трапеции AIFB, являются общими. Коль скоро каждому в отдельности и всем вместе (singulis et omnibus) мгновениям времени AB соответствуют по отдельности и все вместе (singula et omnia) точки линии AB, а проведенные через эти точки параллели, заключенные в треугольнике AEB, представляют градусы возрастающей скорости, тогда как параллели, заключенные внутри параллелограмма, представляют столько же (totidem) градусов скорости не возрастающей и равномерной, ясно, что израсходовано столько же моментов скорости при ускоренном движении соответственно возрастающим параллельным линиям треугольника AEB, сколько при равномерном движении соответственно линиям параллелограмма GB; ибо то, что недостает моментам в первой половине ускоренного движения (ведь моменты, представленные параллельными линиями, заключенными в треугольнике AGI, отсутствуют), возмещается моментами, представленными параллельными линиями треугольника IEF. Отсюда очевидно, что два тела пройдут равные расстояния за одно и то же время, если одно тело, выйдя из состояния покоя, станет двигаться с униформным ускорением, а другое будет двигаться равномерно, соответственно моменту (т. е. градусу. — И.Д.) вдвое меньшему, чем момент максимальной скорости ускоренного движения. Это и требовалось доказать»³.

В этом доказательстве обращают на себя внимание следующие особенности галилеевых рассуждений:

— он опирается на (V ~ t)-отношение, т. е. на утверждение о том, что скорость равноускоренного движения растет прямо пропорционально времени или, говоря современным языком, является линейной функцией времени⁴;

— галилеевы диаграммы движении, представленные треугольником AEB и четырехугольником AGFB, функционируют в его рассуждениях фактически как графики функции V = V(t), иначе все его построения и утверждения потеряли бы смысл (поэтому-то он и проводит два отрезка прямых, из которых один (AB) представляет время, а другой (CD) символизирует пройденный телом путь);

— Галилей использует понятие мгновенной скорости (градус или момент скорости в его терминологии) и устанавливает, как бы мы сейчас сказали, равномощность следующих множеств:

i) бесконечного множества моментов времени временного промежутка AB (MT_AB) и бесконечного множества градусов (моментов) скорости тела, движущегося равноускоренно в течение времени AB (MV_AB):

MT_AB ↔ MV_ab;

ii) бесконечного множества моментов времени временного промежутка AB (MT_AB) и бесконечного множества точек «временно́го» отрезка прямой AB(M_AB):

MT_AB ↔ M_ab;

iii) бесконечного множества градусов скорости MV_AE и бесконечного множества точек на отрезке скорости AE (M_AE):

MV_АE ↔ M_AE;

iv) бесконечного множества отрезков прямых («линий» скорости), параллельных EB (M_EB^{^}) и бесконечных множеств точек MV_AE и M_AB.

M_EB^{^} ↔ MV_AE и M_EB^{^} M_AB

v) бесконечного множества параллельных отрезков прямой («линий» скорости), заключенных в треугольнике AEB (и образующих этот треугольник) M_AEB^{^} и бесконечного множества отрезков прямой, заключенных в четырехугольнике AGFB (и образующих этот четырехугольник) M_AGFB^{^}:

M_AEB^{^} ↔ M_AGFB^{^},

причем «равенство треугольника AEB и четырехугольника AGEB», — а это, по смыслу сказанного Галилеем, могло быть только равенство площадей этих фигур, хотя он избегал слово «площадь», — обосновывается им именно равномощностью этих двух бесконечных множеств;

vi) бесконечного множества возрастающих градусов скорости равноускоренного движения (MV_AB) и бесконечного множества параллельных отрезков прямых («линий» скорости), заключенных в треугольнике AEB M_AEB^{^}:

MV_AB ↔ M_AEB^{^}

vii) бесконечного множества одинаковых градусов скорости равномерного движения, совершающегося в течение времени AB (MV_AB^p) и бесконечного множества одинаковых параллельных отрезков прямых («линии скорости» равномерного движения), заключенных в четырехугольнике AGFB (M_AGFB^{^}):

MV_AB^p ↔ M_AGFB^{^};

viii) бесконечного множества моментов времени временного отрезка AB (MT_AB), бесконечного множества градусов скорости (MV_AE) и бесконечного множества точек пройденного пути CD (MS_CD):

MT_AB ↔ MV_AE ↔ MS_CD,

а следовательно, и

M_AB ↔ M_AE ↔ M_CD,

где M_CD — бесконечное множество точек на отрезке CD, характеризующее пройденный телом путь за время AB.

Из декларированной равномощности («равенства» совокупностей (aggregata) элементов) указанных бесконечных множеств, Галилей делает вывод о равенстве расстояний, проходимых за одно и то же время двумя телами (s₁ = s₂), одно из которых движется равноускоренно из состояния покоя, достигая в конце движения скорость V_max, а другое — равномерно со скоростью V_max/2. Действительно, по Галилею, поскольку

MV_AB^p ↔ M_AGFB^{^} ↔ M_AEB^{^} ↔ MV_AB,

то s₁ = s₂. Но чтобы сделать такой вывод, надо было предположить, что aggregatum отрезков («линий») скоростей, заключенных в треугольнике AEB (M_AEB^{^}) представляет собой расстояние, пройденное равноускоренно движущимся телом за время AB, а aggregatum отрезков («линий») скорости, заключенных в четырехугольнике AGFB (M_AGFB^{^}) — расстояние, пройденное за это же время равномерно движущимся телом. Иначе вывод Галилея оказывается совершенно необоснованным⁵. Поэтому утверждение проф. Ю. Ренна, согласно которому Галилей «не отождествлял эти площади (т. е. площади треугольника AEB и четырехугольника AGFB. — И.Д.) с расстояниями» и «не определял их как представляющие полные скорости (т. е. как velocitas totalis. — И.Д.) соответствующих движений»⁶, представляется мне сомнительным, хотя, действительно, Галилей предпочел оставить вопрос о физическом смысле соответствующих aggregatum за текстом.

Как видим, и в рукописных набросках начала 1600-х гг., и в «Discorsi» (1638) Галилей активно использует протоинфинитезимальные представления⁷. Поэтому далее следует рассмотреть его суждения о структуре континуума более детально. При этом, хотя указанные представления просматриваются в рассмотренных выше и иных рукописных заметках и записях Галилея, для систематического анализа его «инфинитезимальной атомистики» (З. Бехлер) лучше обратиться к текстам «Dialogo» и, особенно, «Discorsi».

Примечания

1. Галилей Г. Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению с приложением о центрах тяжести различных тел // Галилей Г. Избр. труды. Т. II. С. 108—410; С. 234. Т. е. Галилей исходит из «отношения Аристотеля»: если t₁ = t₂, то s₁/s₂ = V₁/V₂.

2. Galilei G. Le Opere. Vol. VIII. P. 208. Перевод В.П. Зубова (Григорьян А.Т., Зубов В.П. Очерки... С. 145).

3. Galilei G. Le Opere. Vol. VIII. P. 208—209. Перевод В.П. Зубова (Григорьян А.Т., Зубов В.П. Очерки... С. 145—146).

4. В Discorsi Галилей признает, что «одно время разделял <...> ложное положение», будто возрастание скорости прямо пропорционально пройденному пути, но затем он его оставил и вот почему: «если скорости стоят друг к другу в том же отношении, что и пройденные или имеющие быть пройденными расстояния, то такие расстояния проходятся в равные промежутки времени: в самом деле, если скорости, с которыми падающее тело проходит расстояние в четыре локтя, вдвое больше скоростей, с которыми оно прошло первые два локтя (Галилей имеет в виду мгновенные скорости, поэтому употребляет множественное число. — И.Д.), ибо одно расстояние вдвое больше другого, то, стало быть, промежутки времени, затраченные для прохождения того и другого расстояния, одинаковы (здесь ГалилеИ исходит из «отношения Аристотеля» (если t₁ = t₂, то s₁/s₂ = V₁/V₂, и наоборот), распространяя его на равномерно ускоренное движение; см. также теорему 2 из первой книги «De Motu locali» (Галилей Г. Беседы... // Галилей Г. Избр. труды. Т. II. С. 236). — И.Д.). Но прохождение одним и тем же телом четырех локтей и двух локтей за один и тот же промежуток времени может иметь место лишь в том случае, если движение происходит мгновенно» (Galilei G. Le Opere. Vol. VIII. P. 203; перевод В.П. Зубова, см.: Григорьян А Т., Зубов В.П. Очерки... С. 236).

5. Впрочем, некоторые историки так и считают. К примеру, М. Клавелен полагает, что процитированное выше и прочие подобные рассуждения Галилея в Discorsi — это не доказательства, а «просто некие упорядоченные перечисления (ordered recapitulations) главных доводов в пользу их (т. е. формулируемых Галилеем утверждений. — И.Д.) принятия» (Clavelin M. Conceptual and Technical Aspects of the Galilean Geometrization of the Motion of Heavy Bodies // Nature Mathematized: papers deriving from the Third International Conference on the History and Philosophy of Science (Montreal, Canada, 1980) / Ed. W.R. Shea. Dordrecht: Reidel, 1983 (Western Ontario Series in the Philosophy of Science, 20). P. 23—50; P. 47).

6. Damerow P., Freudenthahl G, Mc Laughlin P., Renn J., Exploring the Limits... P. 229.

7. Так, например, галилеево представление о площади как о бесконечной «сумме линий» перекликается с геометрической трактовкой определенного интеграла у Лейбница.