10. «Малый комментарий»

В 1877 г. в Вене была обнаружена рукопись астрономического содержания, носившая имя Коперника; в 1881 г. более полный вариант этой же рукописи под названием «Nicolai Copernici de hypothesibus motuum coelestium a se Commentariolus» был обнаружен в библиотеке Стокгольмской обсерватории; недавно найдена еще одна копия той же рукописи в Англии.

В этой рукописи, вероятно не предназначавшейся для опубликования, Коперник предварительно изложил свои взгляды на строение мира. Оригинала рукописи не сохранилось, но, как мы знаем, еще Тихо Браге в изданном в 1603 г. «Введении в обновленную астрономию» («Astronomiae instauratae Progymnasmata») сообщает, что в 1575 г. получил от чешского врача, большого любителя астрономии, Тадеуша Гаека копию труда Коперника, которую он назвал «Tractatus de hypothesibus a se constitutes» — «Трактат о гипотезах, им построенных». Возможно, эта рукопись послужила оригиналом для остальных. По последнему слову названия стокгольмской копии это сочинение называют «Малый комментарий». Его объем небольшой — в издании на русском языке сочинение занимает всего 12 неполных страниц¹.

Относительно времени создания этой рукописи существуют различные предположения — исследователи относили ее ко временам от начала XVI в. до его 30-х годов. Большой заслугой Л.А. Биркенмайера было то, что он показал невозможность написания ее после 1515—1516 гг., но, как мы уже видели выше, и он не смог привязать это сочинение к более точной дате. Между тем определенные указания к датировке содержатся в самом материале, что будет показано ниже.

Начинается «Малый комментарий» следующим образом:

«Наши предки ввели множество небесных сфер, как я полагаю, для того, чтобы сохранить принцип равномерности для объяснения видимых движений светил. Им казалось слишком нелепым, что небесное тело в своей совершенной сферичности не будет всегда двигаться равномерно. Однако они полагали возможным, что при сложении или совместном участии нескольких правильных движений светила будут казаться по отношению к какому-либо месту движущимися неравномерно.

Этого не могли добиться Калипп и Евдокс, старавшиеся получить решение посредством концентрических кругов... Поэтому было сочтено лучшим мнение, что это можно воспроизвести при помощи эксцентрических кругов и эпициклов, с чем, наконец, бо́льшая часть ученых и согласилась.

Первая страница одной из рукописных копий «Малого комментария»

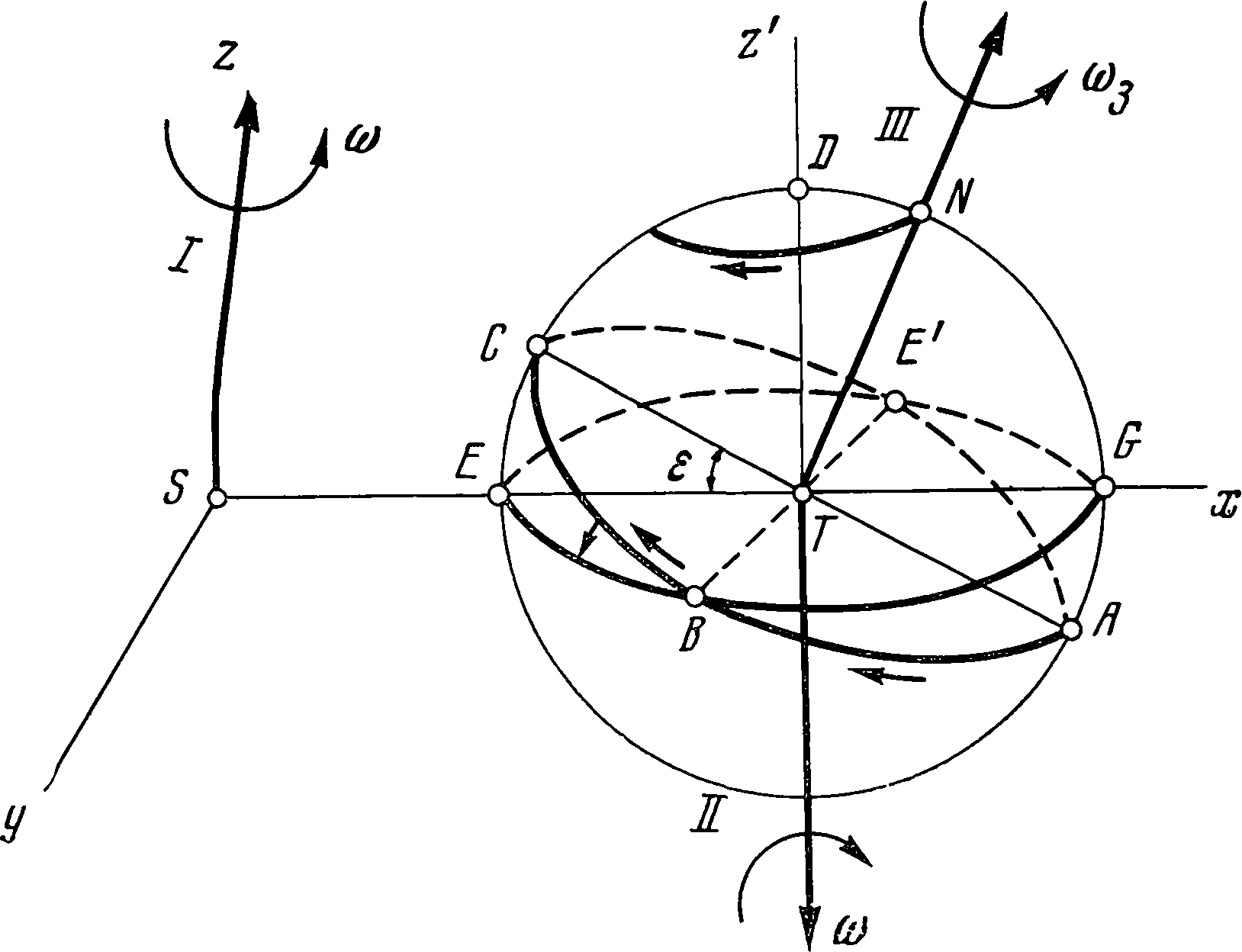
Однако все то, что об этом в разных местах дается Птолемеем и многими другими, хотя и соответствует числовым расчетам, тоже возбуждает немалые сомнения. Действительно, все это оказалось достаточным только при условии, что надо выдумать некоторые круги, называемые эквантами. Но тогда получалось, что светило двигалось с постоянной скоростью не по несущей его орбите и не вокруг собственного ее центра... Я часто размышлял, нельзя ли найти какое-нибудь более рациональное сочетание кругов, которым можно было бы объяснить все видимые неравномерности, причем каждое движение само по себе было бы равномерным... У меня ...появилась мысль, как этого можно добиться при помощи меньшего числа сфер... если только согласиться с некоторыми нашими требованиями, которые называют аксиомами.

Первое требование. Не существует одного центра для всех небесных орбит или сфер.

Второе требование. Центр Земли не является центром мира, но только центром тяготения и центром лунной орбиты.

Третье требование. Все сферы движутся вокруг Солнца, расположенного как бы в середине всего, так что около Солнца находится центр мира.

Четвертое требование. Отношение, которое расстояние между Солнцем и Землей имеет к высоте небесной тверди, меньше отношения радиуса Земли к ее расстоянию от Солнца, так что по сравнению с высотой тверди оно будет даже неощутимым.

Пятое требование. Все движения, замечающиеся у небесной тверди, принадлежат не ей самой, но Земле. Именно Земля с ближайшими к ней стихиями вся вращается в суточном движении вокруг неизменных своих полюсов, причем твердь и самое высшее небо остаются все время неподвижными.

Шестое требование. Все замечаемые нами у Солнца движения не свойственны ему, но принадлежат Земле и нашей сфере, вместе с которой мы вращаемся вокруг Солнца, как и всякая другая планета; таким образом, Земля имеет несколько движений.

Седьмое требование. Кажущиеся прямые и попятные движения планет принадлежат не им, но Земле. Таким образом, одно это ее движение достаточно для объяснения большого числа видимых в небе неравномерностей»².

Коперник опускает математические доказательства, «поскольку они предназначены для более обширного сочинения». Этим сочинением, конечно, могло быть только его бессмертное произведение «О вращениях небесных сфер», работа над которым могла начаться не ранее 1515 г.

Как же представлялась Копернику Солнечная система после допущения суточного вращения Земли? Неподвижный небесный свод, Солнце, которое может быть или неподвижным, или движущимся по эклиптике — кривой, неподвижно связанной с небесным сводом. В отношении вращения Земли могли быть две возможности: ось вращения неподвижна (Земля остается на одном и том же месте) или перемещается. Если считать ось вращения Земли неподвижной, то плоскость, проведенная через центр Земли перпендикулярно оси вращения, будет постоянной. Но эта плоскость пересекает небесный свод тоже по неподвижной кривой (небесному экватору). Таким образом, точка весеннего равноденствия, находящаяся в пересечении двух неподвижных кривых, должна оставаться постоянной и, следовательно, прецессия невозможна. Но она существует. Так как эклиптика неподвижна, небесный экватор должен перемещаться, иными словами, существование прецессии можно объяснить только подвижностью Земли. Таким образом, подвижность Земли является не результатом чисто математического построения, а вполне реальным фактом, доказываемым существованием прецессии. Можно утверждать, что понятие о прецессии неосознанно присутствовало в уме Коперника во время работы над определением движения Земли. Об этом говорит замечание, сделанное им в конце 11-й главы книги первой «Вращений». «Если бы они (годовое обращение центра и деклинационное движение. — Авт.) были в точности равны, то... точки равноденствий и солнцестояний и вся наклонность зодиака ничуть не изменялись бы по отношению к сфере неподвижных звезд. Однако, хотя разница и очень незначительна, она все же обнаружилась, возрастая с течением времени; действительно, от Птолемея до нашего времени эти точки уже прошли навстречу приблизительно на 21 градус»³.

Теперь перед Коперником возникла задача — определить характер движения Земли как твердого тела (в обычном виде эта задача была поставлена лишь через 200 лет после него). Из всех движений твердого тела Копернику были известны только вращательные; он знал также правила их сложений, поэтому и созданная им модель движения Земли имела название теории тройного движения Земли.

Но и сложение вращений не простое дело. Можно складывать только относительное и переносное движения, а если вращений более двух, то при этом приходится придерживаться определенной последовательности. Сложение вращений совсем не то, что сложение сил, для которых действуют законы переместительности и последовательность прибавления сил вполне произвольна.

Для Коперника дело обстояло так. Имеются три объекта: совокупность неподвижных звезд, Земля и Солнце. Звезды неподвижны, Земля движется. А Солнце? Коперник предположил, что оно неподвижно. Эклиптику можно рассматривать как траекторию Солнца или Земли. Чтобы понять ход рассуждений Коперника, мы можем построить две координатные системы. Одна из них будет иметь начало в Солнце S (см. рисунок, римскими цифрами обозначены оси вращения). Плоскость S_xy совпадает с плоскостью эклиптики, а ось S_z перпендикулярна ей. Считаем эту систему неподвижной и к ней будем относить движение Земли. Центр Земли T должен лежать в плоскости эклиптики. Предположим, что в начальный момент он находился на оси S_x. Рассечем Землю плоскостью, перпендикулярной эклиптике. В сечении получается окружность AECDN. Предположим, что в начальный момент на этой окружности находится северный полюс Земли N, тогда прямая TN будет осью суточного вращения Земли. Через центр Земли T проводим плоскость экватора. Пусть AC будет диаметром этого экватора. Заметим, что плоскость сечения AECDN всегда перпендикулярна плоскости эклиптики, но только в начальный момент пересекает ее по неподвижной оси S_x. Задача состоит в том, чтобы, зная, как представляется движение неподвижной системы S_xyz, рассматриваемое с Земли, определить, каково будет движение Земли, наблюдаемое с неподвижной системы S_xyz, или, проще сказать, наблюдателем на Солнце.

Таким образом, рассматриваемое с Земли Солнце S описывает окружность с центром T и радиусом TS. Можно рассматривать данное движение как вращение вокруг проходящей через центр T Земли оси T_z, перпендикулярной плоскости эклиптики, причем вращение совершается против часовой стрелки. Обращая это движение, можно сказать, что оно («наблюдаемое с Солнца») совершается вокруг оси S_z тоже против часовой стрелки; его угловую скорость можно изобразить вектором, направленным по оси S_z. Это первое вращение, по Копернику, а именно годовое: центр Земли T в плоскости эклиптики описывает вокруг Солнца S окружность радиуса ST.

Второе вращение Земли Коперник назвал деклинационным и считал, что от него зависит смена времен года на Земле. Так как первое вращение уже учтено, будем считать центр Земли неподвижным, а чтобы устранить и суточное вращение Земли, будем отмечать видимые положения Солнца в какой-нибудь определенный час дня, положим в полдень. Поскольку мы находимся на Земле, то в качестве неподвижной плоскости можно взять экватор, а в качестве третьей координатной оси — ось Земли TN. Отметим, что угол между плоскостями экватора и эклиптики будет все время постоянным ε = 23°27′). Если отмечать каждый день положение Солнца на графике, то график движения Солнца будет представлять волнообразную кривую: двигаясь по оси времен в одном направлении, Солнце будет попеременно то выше, то ниже экватора. Было ли это движение известно Копернику? Лаврентий Корвин в посвящении к сделанному Коперником переводу Феофилакта Симокатты, говоря о движении Солнца — «брата Луны», употребляет выражение «alternosque meatus fratris» — «попеременные ходы брата». Это как раз описываемое нами движение, о котором Корвин, конечно, знал от Коперника.

Теперь нужно «обратить» это движение. Мы имели неподвижное Солнце, эклиптику и экватор (неподвижный). Нужно взять некоторую точку на экваторе (положим, точку C — конец диаметра) и заставить ее перемещаться вместе с экватором относительно неподвижной эклиптики. В течение года точка C будет попеременно то выше, то ниже плоскости эклиптики. Пусть плоскость эклиптики пересечет поверхность Земли по окружности EBE'. Восстановленный к этой плоскости перпендикуляр T_z' будет неподвижным, так как годовое движение Земли мы уже учли. В таком случае второе движение Земли можно определить как вращение вокруг оси T_z'. В этом движении ось Земли TN будет описывать вокруг оси T_z' коническую поверхность, ибо угол NT_z' = ε имеет постоянную величину. Плоскость экватора Земли ABC, сохраняя постоянный угол ε с плоскостью эклиптики, будет тоже вращаться вокруг оси T_z'. При этом расстояния выбранной точки С от эклиптики EBE' будут изменяться таким же образом, как изменяется расстояние от экватора движущегося по эклиптике Солнца. Оба вращения имеют одинаковый период (один год), но их угловые скорости, сложенные вместе, дадут в сумме нуль.

Сейчас мы знаем, что пара вращений ω—ω производит поступательное движение, но это было установлено только в первой половине XIX в. Коперник термины «поступательное движение» и «пара вращений» не знал, но обращаться с таким движением умел, что можно видеть по его построению второго неравенства движения Солнца (кн. третья, гл. XX). Кроме того, он считает, что «оба эти почти равные друг другу и противоположные движения вместе делают, что ось Земли и наибольшая из ее параллелей — экваториальный круг — смотрят приблизительно в одну и ту же часть мира, как будто бы они оставались все время неподвижными»⁴.

Третье вращение Коперника представляет хорошо известное суточное вращение, совершающееся вокруг оси TN Земли; эта ось теперь оказывается «как будто бы неподвижной».

«Тройное» вращение описано Коперником в XI главе первой книги «Вращений», причем он дает два доказательства его, не считая, очевидно, эту проблему легкой. Действительно, следующее поколение, в частности Галилей, не разобралось в построениях Коперника, а так как коперниканскую систему большинство знает из знаменитых «Диалогов» Галилея, то на вопрос о числе вращений Земли обычно отвечают: «Два — одно вокруг Солнца, другое вокруг оси 3емли». Правильным был бы ответ, что движение Земли состоит из суточного вращения и кругового поступательного движения около Солнца. Эта формулировка появилась только в XVIII в., после работ Даламбера и Эйлера.

Копернику нужно было объяснить не только причину смены времен года, но также и прецессионное движение точки весеннего равноденствия — пересечение экватора с эклиптикой. Так как эклиптика находится на сфере неподвижных звезд, а экватор принадлежит движущейся Земле, то он получает возможность объяснять и явление прецессии:

«Мы говорили, что годовые обращения центра (Земли. — Авт.) и деклинационное являются почти равными; если бы они были в точности равны, то следовало бы, что точки равноденствий и солнцестояний и вся наклонность зодиака ничуть не изменялись бы по отношению к сфере неподвижных звезд. Однако, хотя разница и очень незначительна, она все же обнаружилась, возрастая с течением времени; действительно, от Птолемея до нашего времени эти точки уже прошли навстречу приблизительно на 21 градус. По этой причине некоторые думали, что сфера неподвижных звезд тоже движется ...не достигнув, однако, той цели, какую мы надеемся получить при помощи движения Земли, которым пользуемся в качестве основного принципа и гипотезы для объяснения всего прочего»⁵.

Теперь нам остается сравнить текст «Вращений» с соответствующими местами «Малого комментария», естественно обращая внимание на те моменты, которые могут дать указания на время написания последнего. В главе «О видимых движениях Солнца» «Малого комментария» читаем:

«Земля вращается тройным движением, а именно одним по Великому кругу, обходя Солнце в направлении последовательности знаков (т. е. против стрелки часов. — Авт.) и заканчивая оборот в один год; в одинаковые времена она всегда описывает одинаковые дуги, но центр этого круга отстоит от центра Солнца на 25-ю часть своего полудиаметра»⁶. Таким образом, Коперник полагает здесь эксцентриситет земной орбиты постоянным, как и Птолемей, считавший его равным 24-й части радиуса. Во «Вращениях» эксцентриситет уже считается переменным, изменяющимся между 1/31 и 1/24 (кн. третья, гл. XVI, стр. 206).

В «Малом комментарии» говорится далее:

«В этом движении Солнце будет казаться движущимся неравномерно в соответствии с его расстоянием от центра орбиты... Наибольшее неравенство от этой причины достигает двух градусов с шестой частью. Солнце отклоняется от центра орбиты по направлению к точке небесной тверди, находящейся неизменно (invariabiliter) на расстоянии приблизительно 10 градусов к западу от наиболее блестящей звезды в голове Близнецов»⁷.

Следовательно, Коперник, как и Птолемей, считал положение апогея солнечной орбиты неизменным. В третьей книге «Вращений» (гл. XXII) он считает линию апсид солнечной орбиты перемещающейся.

Далее в «Малом комментарии» читаем:

«Третьим является деклинационное движение... В то время как центр Земли всегда находится в плоскости эклиптики, т. е. окружности Великого круга орбиты, полюсы Земли описывают с обеих сторон небольшие круги с центрами, равно отстоящими от оси Великого круга... Но ось Великого круга сохраняет неизменное положение по отношению к небесной тверди и направлена к так называемым полюсам эклиптики. Деклинационное же движение, сложенное с движением Великого круга, удерживало бы полюсы вращения всегда направленными к одним и тем же местам неба, если бы оно имело с ним совершенно одинаковые времена оборотов. К чему же стремятся прильнуть полюсы — не мое дело говорить. Ведь и у более низменных вещей я вижу, что железный прутик, натертый магнитом, постоянно стремится всегда к одному и тому же месту мира. Однако лучше всего, по-моему, будет предположить, что это все происходит при помощи некоторой сферы, движение которой управляется перемещением самих полюсов; сфера эта, без сомнения, должна быть расположена под Луной»⁸.

Во «Вращениях» это «силовое» определение полностью опущено; там просто указывается, что введение деклинационного движения необходимо для объяснения смены времен года.

Следующая глава «Малого комментария» имеет непосредственное отношение к вопросу относительно определения продолжительности года. Это видно уже из самого названия: «О том, что равномерность движения должна определяться по отношению не к равноденствиям, но к неподвижным звездам». Заканчивается глава такой фразой: «Так мы и сделали и относительно Спики в Деве нашли, что год был всегда равен 365 дням 6 часам и примерно одной шестой часа; таким он был и в египетской древности»⁹. Но первое наблюдение Спики было произведено в 1515 г. («О вращениях», кн. третья, гл. II, стр. 60), и величина звездного года была определена Коперником в 365 дней 6 часов 9 минут 40 секунд (кн. третья, гл. XIV, стр. 190—191).

Это обстоятельство решает дело: значит, «Малый комментарий» был написан примерно около 1515 г. именно в связи с работой Коперника по определению величины тропического года. Мы имеем здесь начало работы, окончание которой было сделано в третьей книге «О вращениях».

Остальная часть «Малого комментария» посвящена движениям Луны и планет. Она представляет интерес в том отношении, что в ней находятся отзвуки теорий Брудзевского, с которыми Коперник познакомился еще в Краковском университете. Брудзевский строил движение Луны и планет исходя из двух эпициклов, тогда как Коперник для воспроизведения планетных движений пользовался системой эксцентр — эпицикл, как и Птолемей. В теоретических расчетах александрийского астронома в движениях планет, как мы уже знаем, отмечались два главных неравенства: неравенство по отношению к зодиаку — мы объяснили бы его тем, что планеты движутся не по кругам, а по эллипсам, и притом неравномерно; это неравенство исправлялось при помощи введения эксцентра, и неравенство по отношению к Солнцу — объяснялось тем, что движение планеты наблюдалось с движущейся Земли, оно учитывалось при помощи эпицикла, которого, по мысли Коперника, можно было бы и не вводить. Он исходил из принципа (правда, не формулируя его явно), который теперь так и называется принципом Коперника: относительное движение двух тел не изменится, если к обоим телам прибавить одинаковое движение.

Сообщая Земле и рассматриваемой планете движения, равные движению Земли, но только направленные в противоположную сторону, мы останавливаем Землю. Тогда планета кроме уже имевшегося движения вокруг Солнца будет иметь еще круговое движение, которое мы увидим в форме движения по эпициклу. Величина этого эпицикла, представляющая собой видимый с Земли круг, описываемый ею вокруг Солнца, будет зависеть от расстояния планеты до Земли: чем дальше планета, тем меньше будет эпицикл. Таким образом, Коперник получил возможность расположить все планеты вокруг Солнца в зависимости от их расстояния до него (кн. первая, гл. X «Вращений»). В результате, как пишет Коперник в «Обращении к папе Павлу III», открывающем его замечательный труд, «...последовательность и величины светил, все сферы и даже само небо окажутся так связанными, что ничего нельзя будет переставить ни в какой части, не производя путаницы в остальных частях и во всей Вселенной»¹⁰.

Примечания

1. См. «Николая Коперника Малый комментарий относительно установленных им гипотез о небесных движениях». В кн. Николай Коперник. О вращениях небесных сфер. Пер. И.Н. Веселовского. «Наука», 1964, стр. 419—430.

2. Николай Коперник. О вращениях..., стр. 419—420.

3. Николай Коперник. О вращениях..., стр. 39.

4. Николай Коперник. О вращениях..., стр. 36.

5. Николай Коперник. О вращениях..., стр. 39.

6. Там же, стр. 421.

7. Там же.

8. Николай Коперник. О вращениях..., стр. 421—422.

9. Там же, стр. 423.

10. Там же, стр. 14.