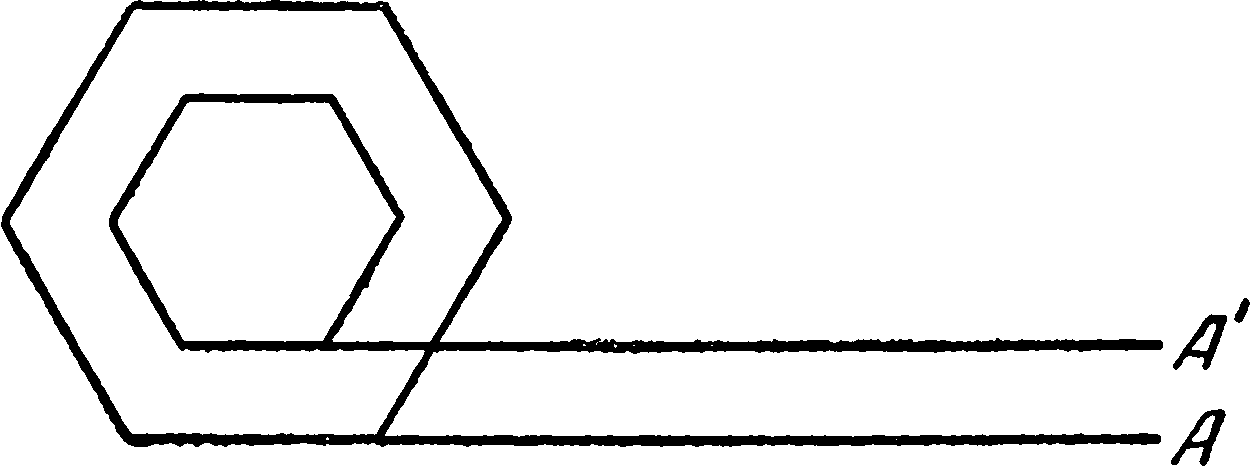
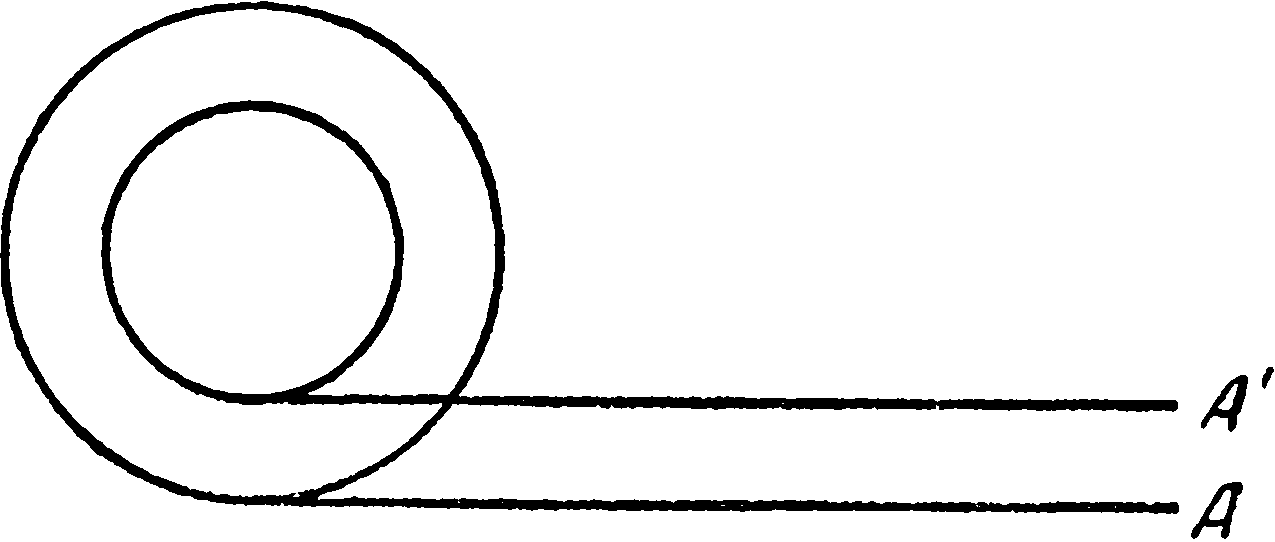
XIV. Учение о веществе

Раскроем «Беседы». Они открываются посвящением графу Ноайлю, французскому послу в Риме, когда-то учившемуся у Галилея в Падуе. В посвящении рассказано, как Галилей, напуганный судьбой «Диалога», хотел передать рукопись иностранному дипломату, чтобы, не выпущенная в свет, она могла стать доступной специалистам.

Граф Ноайль в 1634 г. прибыл в Рим во главе французской миссии, объявившей Урбану VIII, что Ришелье, наконец, решился начать войну против Испании. Это был короткий просвет после ряда неудач, сыпавшихся на Урбана со всех сторон. Посол, привезший столь радостное известие, мог требовать многого. Ноайль попросил папу отпустить Галилея из Арчетри на короткое время, он хотел увидеться с ученым, возвращаясь из Рима во Францию. Осенью 1636 г. Галилей встретил Ноайля между Флоренцией и Сиеной и вручил ему рукопись.

Далее Галилей рассказывает, как он узнал от Эльзевиров, что его книга готова к печати, и решил посвятить ее графу Ноайлю.

«Поэтому Вашему имени, досточтимый синьор, да будет посвящено мое сочинение, сделать это побуждает меня не только сознание всего того, чем я Вам обязан, но и готовность Ваша, да позволено мне будет так выразиться, защищать мою репутацию ото всех, желающих запятнать ее. Вы опять воодушевили меня на борьбу с моими противниками»¹.

И передача рукописи в 1636 г., и ее посвящение, и последние строки в особенности являются как бы символом бегства из-под власти инквизиции. Он мог это сделать только для своих книг. Но и они во Франции не могли получить свободу распространения. Здесь в это время уже не было Декарта, он переселился в Голландию, да и там после процесса Галилея Декарт боялся защищать гелиоцентризм и боялся выпускать книги под своим именем. Но даже хранение и распространение в узком кругу было опасным делом. Великий герцог Тосканы не мог в этом отношении, да и в других, помочь Галилею. Робкие представления герцога были отвергнуты папой.

После посвящения напечатано обращение к читателям от издателей. Здесь говорится о предшествующих открытиях Галилея. Подчеркнуто действительно главное: Галилей убедил людей, потому что наблюдения шли рука об руку с теоретической дедукцией. В этом, как мы видели, состоит характерная эпистемологическая позиция Галилея. Блеск открытий Галилея «свидетельствует о размере заслуг того, кто расширил наше познание и показал столько нового и замечательного в отношении небесных тел, несмотря на их отдаленность от нас, граничащую с бесконечностью, ибо наглядность, говоря обыденным языком, в один день научает нас с большей легкостью и прочностью тому, чему не могут научить правила, повторяемые хотя бы тысячу раз, так как собственное наблюдение (как выражаются некоторые) идет здесь рука об руку с теоретическим определением»².

Но еще более важной заслугой Галилея является изложенная теперь научная концепция явлений, которые были известны с незапамятных времен. «Что должно сделать это сочинение еще более достойным удивления, это то, что одна из наук касается предмета вечного, имеющего первенствующее значение в природе, обсуждавшегося великими философами и изложенного во множестве уже написанных томов, короче сказать, движения падающих тел — предмета, по поводу которого автором изложено множество удивительных случаев, которые до сего времени оставались никем не открытыми или не доказанными. Другая наука, также развитая из основных ее принципов, касается сопротивления, оказываемого твердыми телами силе, стремящейся их сломить, и также изобилует примерами и предложениями, остававшимися до сих пор никем не замеченными; познания такого рода весьма полезны в науке и искусстве механики»³.

В «Беседах» участвуют те же лица, что и в «Диалоге»: Сальвиати, Сагредо и Симпличио. Эти имена могли вызвать новые преследования. Галилея предупреждали об опасности, но он пренебрег советами. Симпличио играет теперь новую роль. Он не спорит, а выполняет чисто дидактическую функцию, его вопросы помогают разъяснить существо дела. Кастелли писал Галилею, что его разочаровала такая роль Симпличио⁴. Но она отвечала духу «Бесед» и, более того, новым объективным требованиям развивавшейся теории движения. Когда беседа касается более сложных проблем, Симпличио исчезает. Его заменяет Апроино. Это имя принадлежало умершему в марте 1638 г. венецианскому аббату — единомышленнику Галилея.

Начало «Бесед» не раз уже упоминалось, и теперь его следует привести полностью. Сальвиати, обращаясь к коренным венецианцам Сагредо и Симпличио, говорит:

«Обширное поле для размышления, думается мне, дает пытливым умам постоянная деятельность вашего знаменитого арсенала, синьоры венецианцы, особенно в области, касающейся механики, потому что всякого рода инструменты и машины постоянно доставляются туда большим числом мастеров, из которых многие путем наблюдений над созданиями предшественников и размышления при изготовлении собственных изделий приобрели большие познания и остроту рассуждения»⁵.

В ответной реплике Сагредо говорит о парадоксальных явлениях, которые ему разъяснили инженеры арсенала. Тут же — полемический выпад против схоластов, впрочем, совсем не такой темпераментный, как в былое время.

«Тут мало помощи оказывает то, что сказал по этому поводу кто-либо из древних, или общераспространенные взгляды и учения, я, напротив, считаю их вовсе лишними, равно как и многие другие объяснения, исходящие из уст людей мало ученых, полагая, что все такие объяснения имеют только одну цель — показать, что можешь сказать что-нибудь о том, чего не понимаешь»⁶.

Понятие парадоксального явления — важное понятие галилеевой эпистемологии. Оно не может войти ни в феноменологическую, ни в априорную концепцию. Эйнштейн говорил о переходе от парадоксального явления к парадоксальной теории как об основном пути, приведшем к принципу относительности, и вообще как о своем основном творческом методе.

В автобиографическом очерке 1948 г. Эйнштейн рассказывает о том глубоком удивлении, которое вызвала у него в детстве магнитная стрелка. В этой связи он высказывает весьма существенные эпистемологические соображения⁷. Магнитная стрелка — парадоксальный факт с точки зрения механического представления, ограниченного понятием толчка. Если построить логически непротиворечивую теорию магнитного поля, парадоксальную с точки зрения привычных представлений, движение магнитной стрелки перестает быть парадоксальным. Аналогичным образом была создана специальная теория относительности. Опыт Майкельсона и другие оптические опыты привели к парадоксальному результату: скорость света в данной системе не зависит от ее движения. Попытка согласовать этот результат с классической механикой Ньютона и придать постоянству скорости света чисто феноменологический смысл (лоренцова гипотеза абсолютного сокращения масштабов) не обладала «внутренним совершенством», она включала выдвинутую ad hoc, не вытекавшую из общих соображений произвольную гипотезу. Тогда Эйнштейн высказал парадоксальную общую теорию: он отказался от абсолютного пространства, от абсолютного времени, от эфира, от классического правила сложения скоростей. Результаты Майкельсона потеряли свою парадоксальность.

Когда была создана общая теория относительности, исходное явление — одинаковая скорость падения тел — уже не казалось парадоксальным с точки зрения привычных наблюдений. Во времена Галилея трудно было поверить, что тяжелое тело падает не быстрее, чем легкое, но теперь к этому привыкли. Именно привыкли: равенство тяжелой и инертной масс не вытекало из более общего принципа и казалось случайным. Поэтому факт равной скорости падения сохранял логическую парадоксальность. Предположение о тождестве тяготения с кривизной пространства-времени — крайне парадоксальное предположение — лишило тождество инертной и тяжелой масс его парадоксальности.

Но в обоих случаях — и в специальной и в общей теории относительности — новая общая идея интуитивно предвосхищала новые эксперименты, новые подтверждения. Путь Эйнштейна был близок «экспериментальному рационализму» Галилея. Специальная теория была подтверждена колоссальным множеством новых фактов, об нарушенных физикой атома, ядра и элементарных частиц. Общая теория относительности ограничивается пока скромным числом подтверждений — значительно менее определенных.

Парадоксальный факт, которым начинаются «Беседы», — это возможность поломки судна вследствие давления его собственного веса. Сальвиати говорит об этом явлении. Сагредо ему отвечает:

«Этот факт и в особенности последнее замечание, сделанное но поводу него, которое обыкновенно понимается людьми неправильно, показывают, что относительно этих и других механизмов нельзя делать заключения от малого к большому, многие изобретения в машинах удаются в малом, но неприменимы в большом масштабе. Однако вся механика имеет своею основою геометрию, и мы знаем, что круги, треугольники, а также цилиндры, конусы и другие формы твердых тел не только отличаются друг от друга большей или меньшей величиной, но и изменяются одни по одним, а другие по другим законам. Если поэтому большая машина сделана во всех своих частях пропорционально малой, оказавшейся прочною и пригодной для употребления, то я не вижу, почему мы все же не можем считать себя обеспеченными от какого-либо несчастий или опасности»⁸.

Иногда это расхождение между геометрическим подобием и механическими свойствами объясняют принципиальным отличием материальных процессов от геометрических соотношений: материя в геометрическом смысле несовершенна. Сальвиати несогласен с таким объяснением. Конструкции из абсолютно неизменного и однородного вещества также обнаружили бы отсутствие механического подобия. Сальвиати говорит, что такое вещество не может не подчиняться геометрическим соотношениям. «Значит, существуют собственно математические эквиваленты отсутствия механического подобия: «это важное и неизбежное явление дает основание для вполне ясных чисто математических рассуждений».

Реплика Сальвиати позволяет, пока еще интуитивно, предположить существование парадоксальной математической теории, которая устраняет парадоксальность наблюдаемого факта. «Я уже чувствую, — отвечает Сагредо, — как меняются мои мысли, подобно тому, как облако озаряется мгновенно молнией, так и мой ум озарился внезапным и необычным светом, который затем опять погас, показав только издали странные и непривычные представления»⁹.

Мы вскоре увидим, что речь идет о совершенно парадоксальной, с точки зрения перипатетического учения, атомистической теории вещества, выражающей дифференциальное представление о материи. Но сейчас эти «странные и непривычные представления» только мелькнули в уме, «озаренном внезапным и непривычным светом».

Далее беседа переходит к проблеме знаменитой horror vacui — свойственной природе боязни допустить хотя бы на время пустоту. Галилей показывает, что концепция Аристотеля не может объяснить прочность тел и вводит в игру новое понятие — микроскопических пустот в веществе. Сальвиати говорит о гипотезе («выдаю это не за достоверную истину, но за идею, нуждающуюся в развитии»): плавление металлов объясняется проникновением частиц огня в микроскопические поры металла, исчезновение пустот устраняет силы сцепления в металле, и металл становится жидким.

Но не эта неоднозначная физическая концепция интересует Галилея. Его интересует проблема бесконечности пустот в теле. И здесь мы подходим к проблеме континуума. В июне 1634 г. Кавальери, закончивший «Geometria indivisiblium», послал Галилею письмо, в котором просил разобраться в вопросе о бесконечно малых в связи с движением¹⁰. Мы увидим в следующей главе, как Галилей в «Беседах» обобщил и конкретизировал идею бесконечного множества мгновенных состояний движущегося тела. Но он применил понятие бесконечности и к вопросу о структуре вещества и именно в этой связи произвел сравнительно систематический разбор этого понятия.

Речь идет о микроскопических пустотах, существование которых объясняет прочность тел. Существование таких пустот заставляет разделенные пустотами частицы тела стремиться одна к другой. Отсюда следует, что в очень малых частях тел, где уже нет пустот, ничто не гарантирует прочности тел. Но, быть может, число пустот окажется бесконечно большим? Именно этот вопрос задает Сагредо. Сальвиати отвечает:

«Раз мы уже дошли до парадоксов, то попробуем, нельзя ли каким-либо образом доказать, что в некоторой конечной непрерывной величине может существовать бесконечное множество пустот»¹¹.

Сальвиати рассматривает одну очень старую, идущую от древности проблему¹². Представим себе некоторый многоугольник, например шестиугольник, внутри которого находится подобный ему, концентрический меньший многоугольник. Каждый из них лежит одной стороной на прямой — продолжении этой стороны. Оба многоугольника соединены и когда больший многоугольник начинает перекатываться по прямой A так, что с ней последовательно совпадают его стороны, он увлекает меньший многоугольник. Стороны меньшего многоугольника откладываются на прямой A′.

Качение многоугольников означает, что больший из них в течение определенного числа вращений пройдет расстояние, равное его стороне, помноженной на число таких сторон, последовательно совместившихся с прямой. Меньший многоугольник пройдет расстояние, равное его стороне, помноженной на то же число. Стороны различны, и кажется очевидным, что меньший многоугольник отложит на своей прямой меньшее пройденное расстояние. Но, столь же очевидно, многоугольники пройдут приблизительно равные пути. Каков же выход из противоречия? Сальвиати говорит, что на прямой A′, наряду с отрезками, совпадавшими со сторонами меньшего многоугольника, находятся «пустоты» — отрезки, к которым многоугольник при качении не прикасался своим периметром.

Далее Сальвиати переходит от многоугольника к кругу — многоугольнику с бесконечным числом сторон. Две концентрические окружности касаются каждая своей прямой. Ограниченные ими круги катятся, причем меньший круг соединен с большим.

Здесь выход из йротйворечия тот же, что и в случае многоугольника, но теперь число «пустот» должно быть бесконечным:

«Линия, образуемая непрерывным наложением бесконечно большого числа сторон большого круга, приблизительно равна по длине линии, образованной наложением бесконечно большого числа сторон меньшего круга, если включить в нее и наличные промежутки, а так как число сторон не ограничено, а бесконечно, то и число промежутков между ними также бесконечно, бесконечное множество точек в одном случае занимает пространство полностью, в другом — пространство занято бесконечным множеством точек и пустых промежутков. Я хотел бы, чтобы вы заметили себе, что, разделяя линию на некоторые конечные и потому поддающиеся счету части, нельзя получить путем соединения этих частей линию, превышающую по длине первоначальную, не оставляя пустых пространств между ее частями, но линию, разделенную на бесконечное число частей, т. е. составленную из неделимых бесконечно малых частиц, мы можем представить себе простирающейся без прерывания конечными пустотами, но включающей бесконечное множество малых неделимых пустых пространств»¹³.

Далее Сальвиати переходит к веществу — к растягиванию золотого шарика в очень большой лист и к тому подобным примерам. Сальвиати говорит, что при этом в веществе не появляется конечных пустот, а сохраняются бесконечно малые пустоты. В конечном по размерам теле — бесконечное число бесконечно малых пустот и бесконечно малых частиц.

Здесь Симпличио указывает на сходство этого взгляда с взглядами «одного древнего философа». Речь идет о Демокрите — его имя было тогда под запретом.

«Надеюсь, что вы не прибавите «отрицавший божественный промысел», как это весьма неуместно сделал в случае, подобном нашему, один из противников нашего академика»¹⁴, — говорит Сальвиати. В ответ Симпличио заверяет собеседников в отсутствии у него подобных намерений. Беседа продолжается. Пока еще неясно, каково природа бесконечно малых атомов вещества. Неясна и позиция Галилея в математической проблеме бесконечно малых. После дискуссии XVIII в. об «исчислении нулей», после ряда схем обоснований анализа в XIX в., нам хочется точнее определить, что представляют собой бесконечно малые Галилея. Здесь можно следовать за текстом «Бесед», Сальвиати, Сагредо и Симпличио переходят к понятию бесконечно малой величины.

На вопрос Симпличио, можно ли представить себе линию, состоящую из точек, т. е. нечто делимое, состоящее из неделимых элементов, Сальвиати отвечает:

«Такие затруднения действительно существуют, равно как и многие другие, но вспомните о том, что мы имеем дело, с одной стороны, с величинами бесконечно большими, с другой, с бесконечно малыми, неделимыми, постичь которые умом невозможно, благодаря необъятности одних и малости других. Мы убеждаемся здесь, что человеческая речь не приспособлена для выражения таких понятий. Однако я все же позволю себе изложить некоторые свои соображения, которые хотя и не исчерпывают вопроса, но могут представить некоторый интерес благодаря своей новизне. Впрочем, столь частые уклонения в сторону от начатого пути, быть может, покажутся вам неуместными и маложелательными?»¹⁵

Этот первый тезис очень многозначителен. Человеческая речь не приспособлена для выражения таких понятий, как бесконечно большое и бесконечно малое. Речь легко справляется с понятием конечных величин. Может быть, привычные, отложившиеся в языке понятия предполагают статическую схему мироздания? Может быть, именно эта статическая картина не может вместить бесконечность? Ведь именно существующая, актуальная, наличная, достигнутая, статическая бесконечность кажется наиболее тяжелым испытанием для мысли и конкретного представления.

Сальвиати становится на путь, который ведет к новому представлению о бесконечности. Он спрашивает, не покажется ли неуместным новое уклонение от прямой темы собеседования. Сагредо отвечает настойчивой просьбой продолжать обсуждение проблемы бесконечности и воспользоваться преимуществами живой беседы перед изучением мертвых книг. Тогда Сальвиати ставит кардинальный вопрос: можно ли считать точку и линию равновеликими? Оказывается, можно: можно уменьшать равновеликие тела так, чтобы они, оставаясь равновеликими, стягивались — одно в линию, а другое в точку. Это геометрическое построение нужно Сальвиати, чтобы разбить привычку пользоваться в мире бесконечного понятиями, пригодными для конечных величин. Теперь начинается позитивная часть задачи. Сальвиати связывает воедино проблему бесконечно большого и проблему бесконечно малого. Они в равной степени непостижимы, но, пользуясь ими как связанными понятиями, можно прийти к положительным выводам.

«Я хочу высказать, — говорит Сальвиати, — одну особую мысль, повторяя то, что было сказано мною незадолго перед этим, а именно, что бесконечное для нас, по существу, непостижимо, равно как и последнее неделимое. Представьте себе, что будет, если соединить и то и другое, если мы хотим составить линию из неделимых точек, то мы должны взять бесконечное множество их, таким образом мы познаем одновременно и бесконечное и неделимое»¹⁶.

Галилей не рассматривает бесконечность как результат сложения величин. Он рассматривает бесконечность как результат деления конечной величины. Ее делят на бесконечное множество бесконечно малых элементов.

У Симпличио напрашивается весьма существенный вопрос. Если два неравных отрезка представляют собой бесконечные множества точек, то одно бесконечное множество оказывается больше другого.

В ответ Сальвиати высказывает ряд соображений, которые почти нет нужды сравнивать с современными взглядами: и сходство, и различие понятий, и соблазны, и опасности модернизации видны здесь сразу.

Прежде всего понятия «больше» и «меньше» неприменимы к бесконечным множествам.

«Сказанное вами, — отвечает Сальвиати на вопрос Симпличио, — относится к числу затруднений, происходящих вследствие того, что, рассуждая нашим ограниченным разумом о бесконечном, мы приписываем последнему свойства, известные нам по вещам конечным и ограниченным. Между тем это неправильно, так как такие свойства, как большая или меньшая величина и равенство, неприменимы к бесконечному, относительно которого нельзя сказать, что одна бесконечность больше или меньше другой или равна ей»¹⁷.

Бесконечное число не имеет свойств конечных чисел. Сальвиати иллюстрирует эту мысль примером. Множество квадратов меньше, чем множество всех чисел (не все числа являются квадратами), но оно равно множеству корней (каждый квадрат имеет корень), а это последнее равно множеству всех чисел (каждое число может быть корнем квадрата).

Теперь беседа переходит к бесконечно малым отрезкам линии как непрерывного целого. Симпличио приписывает им — по традиции — и конечность и бесконечность. Они бесконечны лишь в потенции. Сальвиати выдвигает иную точку зрения. Элементы непрерывного целого ни конечны, ни бесконечны. Здесь прорывается очень неясный намек на понимание бесконечно малой как переменной величины. Сальвиати (поскольку речь идет уже не столько о репликах, сколько об идеях, можно было бы сказать: Галилей) рассматривает ряд величин между конечной величиной и бесконечной. Между ними находится нечто третье — не конечная и не бесконечная величина: «среднее, соответствующее любому данному числу»¹⁸ (un terzo medio termine, che à il rispondare ad ogui segnato numero). Эта третья величина, «соответствующая любому данному числу», т. е. величина, не имеющая постоянного, одного и того же значения, может быть половиной, четвертью и т. д. целого. Но она может быть и бесконечно малой частью целого.

Симпличио отвечает Сальвиати серьезным замечанием. Как ни трудно фактически разделить целое на очень большое число частей, эта трудность отличается от принципиальной и абсолютной невозможности реального разделения целого на бесконечное множество частей.

«Но если я сведу это деление, признаваемое вами вовсе невозможным, к такому же короткому процессу, как тот, который требуется другим для разделения линии на сорок частей, то будет ли этого для вас достаточным, чтобы уделить ему место в нашей беседе?»¹⁹

Симпличио считает это шуткой. Но Сальвиати предлагает следующий чрезвычайно остроумный, наглядный и логически безупречный метод непосредственного разделе-ния линии на бесконечное множество бесконечно малых частей. Разделить конечную линию на две части, на три и т. д. можно, перегибая ее посередине или в двух точках, отсекающих три равные отрезка, и т. д. Возможно «относительно строгое доказательство того, что подобное сгибание делит линию на любое множество частей. Если же сложить линию в окружность, то мы сразу получим бесконечное число изгибов и, соответственно, бесконечное число точечных элементов линии.

«Вы не можете отрицать, — говорит Сальвиати, — что подобное рассуждение не менее верно в отношении бесконечного множества частей линии, нежели в отношении четырех частей, образующих квадрат, или тысячи частей, образующих тысячеугольник, потому что в нем не нарушается ни одно из условий, имеющихся для многоугольника с тысячью или ста тысячами сторон. Последний, поставленный на одну из своих сторон и приложенный к прямой линии, соприкасается с ней этой стороной, т. е. одной стотысячной своей частью; круг, который представляет собою многоугольник с бесконечным числом сторон, соприкасается с прямой также одною из своих сторон, т. е. единственной точкой, отличной от других соседних, а потому отделенной и отграниченной от них не в меньшей степени, нежели отделена от соседних сторона любого многоугольника»²⁰.

Итак, линия разделена на бесконечное множество точек. Намек на представление о бесконечно малой величине как о переменной не реализован. Концепция Галилея — это концепция бесконечно малых частей линии — отрезков нулевой протяженности, точек.

Мы увидим вскоре, что Галилей подошел к более близкому нам представлению о бесконечно малых в теории движения. Вообще инфинитезимальные идеи Галилея очень отчетливо демонстрируют связь анализа с кинетическими проблемами²¹. Весьма далекое еще от аналитических понятий конца столетия представление о точечных элементах, высказанное в связи с теорией вещества, играло другую роль.

Высшее выражение дифференциального представления о движении — аналитическая механика Лагранжа — было, как уже сказано выше, синтезом аналитического представления о траектории частицы как о бесконечном множестве геометрических точек и физического представления о материальной точке, которая действительно проходит по траектории. Правда, можно пользоваться представлением о приближенно точечной массе, о частице, размерами которой мы пренебрегаем. Можно представить себе материальную точку как центр тяжести протяженного тела. Но этими представлениями можно пользоваться, когда уже возникло понятие непротяженного материального элемента — физической, материальной точки. Именно такое понятие превращает линию в траекторию, а описывающую эту линию функцию — в закон движения.

Галилей пользуется понятием бесконечно малых, неделимых элементов вещества, чтобы высказать некоторые собственно физические теории. Но они остаются примерами геометрических соотношений, вернее, они играют роль «физикализаторов» геометрических соотношений.

Такова концепция различия между жидкостью и измельченным твердым телом. Сальвиати разъясняет физическую реальность бесконечно большого объекта — результата сложения конечных величин.

«Подумайте теперь, — говорит он, — какая разница существовала между кругом конечным и бесконечно большим. Последний настолько изменяет свою сущность, что окончательно теряет свое существование как таковой и даже самую возможность существования; теперь мы совершенно ясно понимаем, что не можем создать бесконечно большой круг, отсюда как следствие вытекает, что не может быть ни бесконечно большого шара, ни другого бесконечного тела, ни бесконечно большой поверхности. Что скажем мы о таких метаморфозах при переходе от конечного к бесконечному? И почему, стремясь найти бесконечность в больших числах, мы должны чувствовать неудовлетворенность, придя к выводу, что она выражается единицею? Когда мы разбиваем твердое тело на многие части, постепенно превращаем его в мельчайший порошок, предполагая, что оно разделяется на бесконечное множество своих атомов, не делимых далее, то почему не можем мы сказать, что такое тело возвратилось к состоянию непрерывному, но жидкому, как вода или ртуть или другой расплавленный металл? И разве мы не видим, как камни расплавляются в стекло и само стекло делается на большом огне жидким, как вода?»²²

Эта реплика по существу эквивалентна той, где деление на бесконечное множество элементов демонстрируется свертыванием линии в круг. Здесь тот же прием, но он совершенно физический: твердое тело, состоящее из конечного числа конечных элементов, превращается в жидкое тело, состоящее из бесконечно большого множества бесконечно малых элементов.

Симпличио, выслушав приведенную реплику Сальвиати, спрашивает:

«Должны ли мы думать, что жидкости таковы, как они есть, потому что они разложены на бесконечное число первоначальных неделимых частиц, их составляющих?»²³

Сальвиати отвечает, что именно таково отличие жидкостей от измельченных твердых тел. Он приводит множество физических доказательств: самые тонкие порошки, в отличие от жидкости, не растекаются по поверхности, стекло при дроблении теряет прозрачность, а вода — нет, и т. д.

«Отсюда, кажется мне, можно вполне основательно заключить, что частицы воды, из которых она, по-видимому, состоит (более тонкие, нежели любой мельчайший порошок, и лишенные всякой устойчивости), весьма отличны от частиц конечных и делимых, и я не могу найти причины различия иначе, как в том, что они неделимы»²⁴.

Это очень характерная для Галилея концепция: различие между измельченным твердым телом и жидкостью объясняется количественной несоизмеримостью дискретных частей вещества.

Далее речь заходит о другом физическом вопросе — разрежении и сгущении вещества — и затем об одном из центральных пунктов «Бесед» и мировоззрения Галилея в целом — доказательстве равной скорости падения тел в пустоте. Здесь находится, помимо прочего, решающее звено идеи бесконечного множества точек, из которых состоит пройденное материальной точкой пространство, и мгновений, из которых состоит время, когда эта точки двигалась.

Примечания

1. Ed. Naz., VIII, 44 («Беседы», 35).

2. Ed. Naz., VIII, 46 («Беседы», 39).

3. Ed. Naz., VIII, 46 («Беседы», 39—40).

4. Ed. Naz., XVIII, 26.

5. Ed. Naz., VIII, 49 («Беседы», 47).

6. Ed. Naz., VIII, 49—50 («Беседы», 48).

7. Albert Einstein. Philosopher-Scientist. Ed. by P. Schilp. N. Y., 1951, p. 8. Русск. перевод: «Успехи физии, наук», т. 59, вып. 1, 1956, стр. 73—74.

8. Ed. Naz., VIII, 50 («Беседы», 48—49).

9. Ed. Naz., VIII, 51 («Беседы», 50—51).

10. Ed. Naz., XVI, 103.

11. Ed. Naz., VIII, 68 («Беседы», 78).

12. Она была изложена в приписывавшихся Аристотелю «Проблемах механики», гл. XXV (см., например, перевод Poselger: Aristoteles Mechanische Probleme — Questiones Mechanicae. Hannover, 1881).

13. Ed. Naz., VIII, 71—72 («Беседы», 84—85).

14. Ed. Naz., VIII, 72 («Беседы», 86).

15. Ed. Naz., VIII, 73 («Беседы», 87).

16. Ed. Naz., VIII, 76—77 («Беседы», 93).

17. Ed. Naz., VIII, 77—78 («Беседы», 95).

18. Ed. Naz., VIII, 81.

19. Ed. Naz., VIII, 82 («Беседы», 103).

20. Ed. Naz., VIII, 92 («Беседы», 120—121).

21. См.: Ф. Энгельс. Диалектика природы. К. Маркс и Ф. Энгельс. Сочинения, 2 изд., т. 20, М., 1961, стр. 587.

22. Ed. Naz., VIII, 85 («Беседы», 107—108).

23. Ed. Naz., VIII, 85 («Беседы», 108).

24. Ed. Naz., VIII, 86 («Беседы», 109—110).