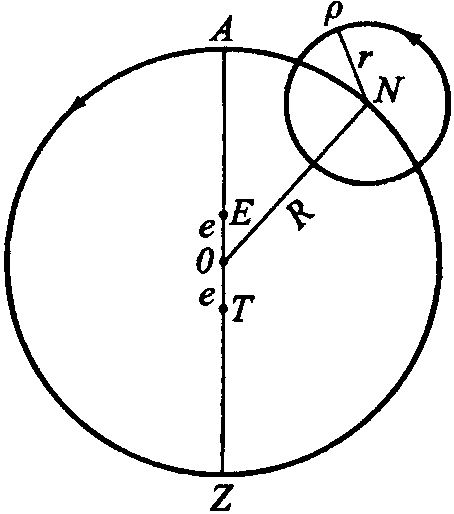Геометрическое интермеццо, или «Общая схема наших ухищрений»¹

В погибшем мире веровать привыкли,
Что излучения буйной страсти льет
Киприда, движась в третьем эпицикле.

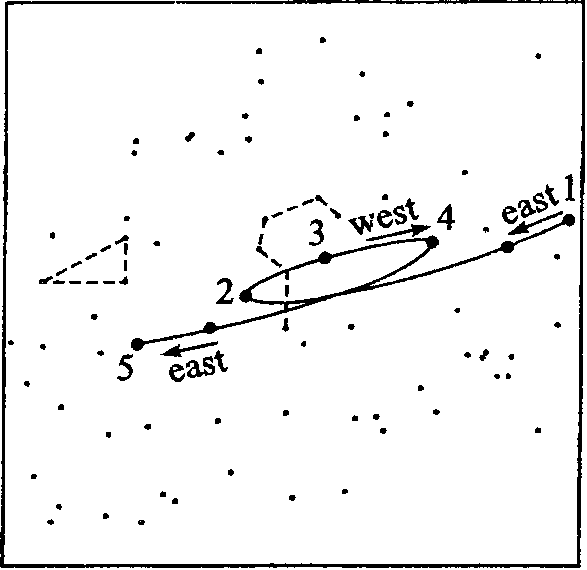
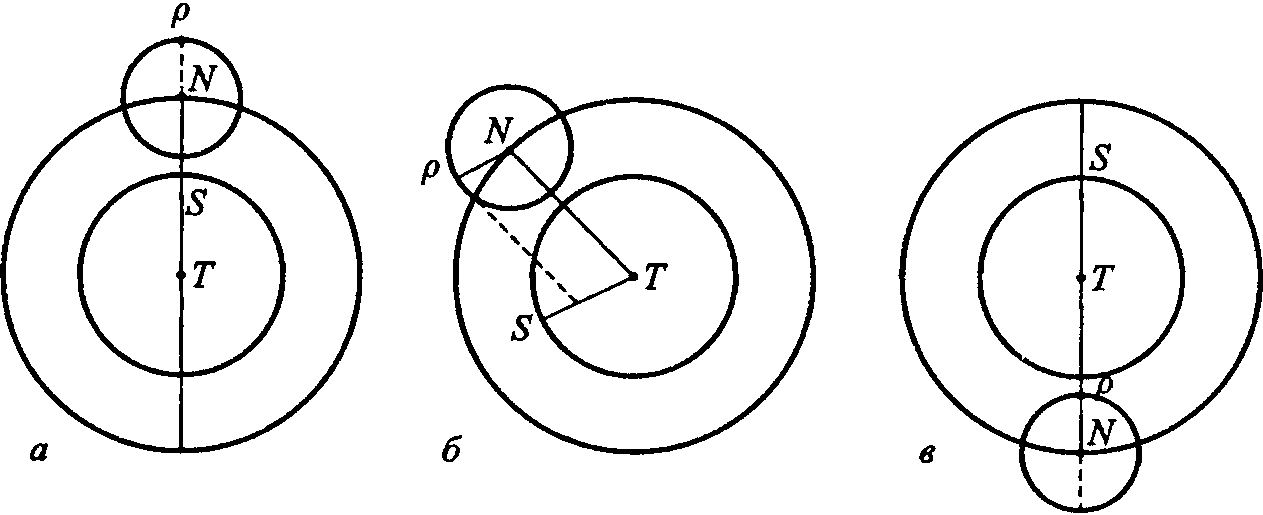
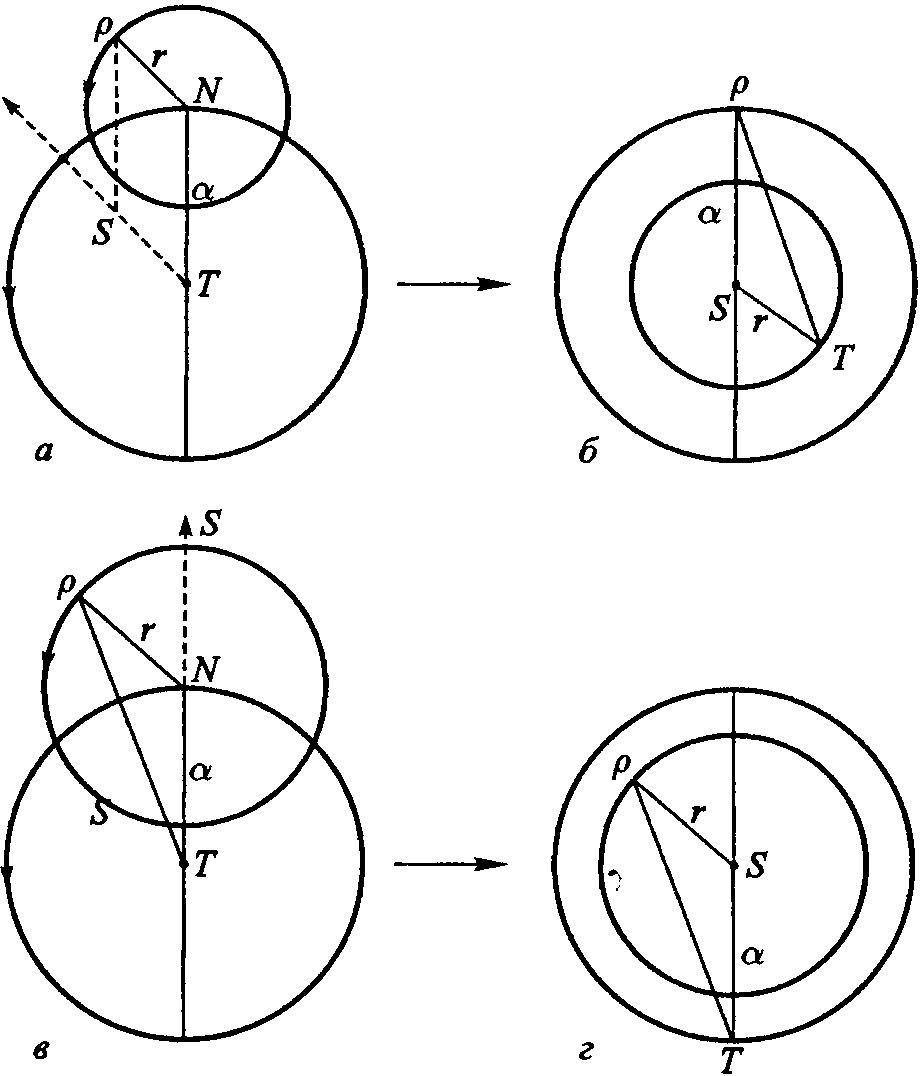
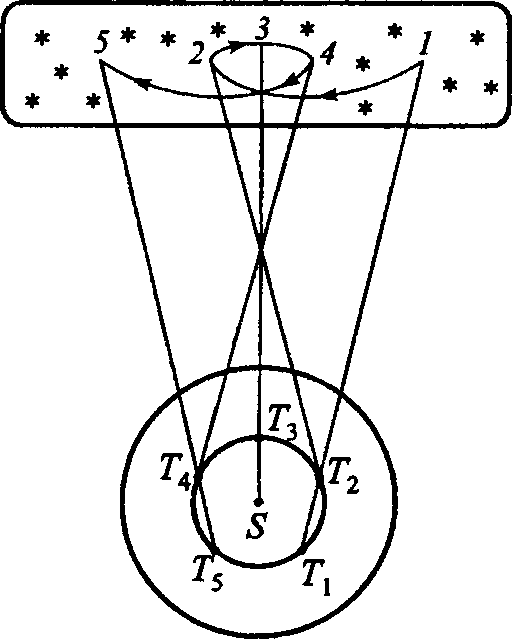
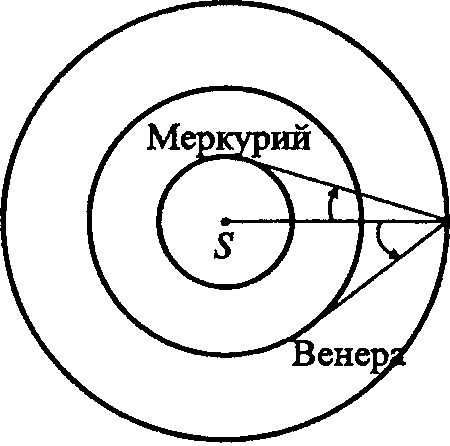
Данте Алигьери

Согласно теории Птолемея, который в свою очередь опирался на идеи Гиппарха (160—126 гг. до н. э.), Апполония Пергского (III в. до н. э.) и других астрономов, движение любой планеты (кроме Солнца) можно представить так, как показано на рис. 1. Планета P равномерно движется по окружности с центром N. Эта окружность называется эпициклом (circulus epicyclus). В свою очередь, центр эпицикла N равномерно движется в ту же сторону², что и P, по другой окружности большего радиуса с центром O, которая называется деферентом (circulus deferens). Таким образом, точка P участвует в двух круговых движениях. Подбирая величины скоростей движения точки P по эпициклу и точки N по деференту и вводя ряд дополнительных условий, можно описать движение каждой планеты, каким его видит земной наблюдатель, находящийся в точке T.

Птолемей и его предшественники исходили из того, что небесные движения должны быть круговыми и равномерными или, по крайней мере, наблюдаемое движение планеты должно быть представлено как «сумма» равномерных круговых движений³. Видимые движения планет весьма сложны — неравномерны (относительно Земли), петлеобразны (рис. 2), расстояние «планета — Земля» непостоянно и т. д.

Рис. 1. Движение планеты согласно эпициклической теории; R — радиус деферента; r — радиус эпицикла.

По теории Птолемея получалось, что центр эпицикла (точка N) движется относительно точек O и T неравномерно. Чтобы как-то обойти эту трудность, Птолемей ввел еще одну замечательную точку на оси апсид AZ — точку E (точку экванта), расположив ее так, что EO = OT, и показал, что относительно этой точки движение центра эпицикла будет казаться равномерным⁴. Таким образом, в его теории движение планеты является равномерным не относительно «собственного центра» движения, но относительно некоторой точки на оси апсид, что противоречило исходному принципу равномерного кругового движения. «Это и подобные соображения, — писал Коперник, — дали нам повод поразмыслить о подвижности Земли и иных способах, которые сохраняли бы принцип равномерности и другие основы науки...»⁵

По характеру своего движения планеты делились на две группы. К первой относили те, которых, по выражению Птолемея, «Солнце всегда обгоняет». Это — так называемые верхние (другое название — внешние) планеты: Сатурн, Юпитер, Марс. Ко второй группе относили так называемые нижние (или внутренние) планеты⁶ — Меркурий и Венеру, каждая из которых то обгоняет Солнце, то, при попятном движении, сближается с ним, при этом Меркурий удаляется от Солнца не более, чем на 28°, а Венера — не более, чем на 48°, т. е. эти планеты как бы «сопровождают» Солнце, поэтому их трудно наблюдать в его лучах («нелегко увидать такое пятнышко под сильнейшим освещением», — писал Коперник⁷), и их не видно ночью, когда Солнце опускается за горизонт более, чем на 46°. Особым характером движения обладают Солнце (оно движется по деференту, т. е. радиус его эпицикла равен нулю) и Луна.

Рис. 2. Наблюдаемое регрессивное движение Марса (октябрь 1994 — июль 1995). В точке 3 (11 февраля 1995) Марс находился в оппозиции Солнцу (Lattis J.M. Between Copernicus and Galileo: Christoph Clavius and the Collaps of Ptolemaic Cosmology. Chicago & London: The University of Chicago Press, 1994. P. 49)

Уже в древности астрономами были установлены некоторые особенности движения планет, которые требовали своего объяснения. Вот один из примеров, иллюстрирующий особенности птолемеевского подхода к описанию планетных движений. Для определенности я ограничусь случаем верхних планет. Время от времени та или иная планета оказываются на одной прямой с Землей и Солнцем. Так, для верхних планет конфигурация Земля (T) — Солнце (S) — планета (P) — так называемое соединение (или конъюнкция) планеты с Солнцем — имеет место, только когда планета P оказывается в апогее своего эпицикла (рис. 3, а), т. е. на наибольшем удалении от Земли; тогда как конфигурация S — T — P, называемая противостоянием (оппозицией) планеты Солнцу, имеет место, только когда планета P находится в перигее своего эпицикла (рис. 3, в), т. е. ближе всего к Земле. И когда планета приближается к этому положению, земной наблюдатель фиксирует «попятное» движение планеты, т. е. имеет место совпадение трех феноменов — оппозиция верхней планеты Солнцу, ее нахождение в перигее своего эпицикла и ее «попятное» движение (регрессия, retrogressions). Чтобы объяснить эти феномены, Птолемею пришлось ввести дополнительное условие в кинематико-геометрическую схему движения верхних планет, а именно — радиус эпицикла (PN) должен быть всегда параллелен направлению от Земли на Солнце (TS) (рис. 3, б)⁸.

Наконец, следует отметить, что Птолемей фактически вынужден был создать несколько моделей: для верхних планет, для Венеры, для Меркурия, для Луны и для Солнца.

Рис. 3. Движение верхней планеты относительно Земли и Солнца (для простоты принято, что e = 0, т. е. Земля (T) находится в центре деферента

Теория Птолемея могла объяснить многие феномены и закономерности планетных движений — регрессии, оппозиции и сопряжения планеты с Солнцем и т. д. Но, так сказать, по отдельности. Его теория не устанавливала необходимых связей между отдельными закономерностями, ее параметры (скорость движения планеты по эпициклу, скорость движения центра эпицикла по деференту, отношение радиусов эпицикла r и деферента R) определялись из наблюдений, между ними не было необходимой связи, поэтому их и можно было соотнести друг с другом так, чтобы спасти явления. Иными словами, теория Птолемея была слишком гибкой и потому маловосприимчивой к процедуре опровержения. Правда, одна закономерность, выявляемая этой теорией, казалось бы, составляет исключение: можно показать, что при r < R регрессии верхних планет могли иметь место только при условии, что угловая скорость обращения планеты по эпициклу меньше угловой скорости вращения центра эпицикла по деференту. Но при внимательном рассмотрении оказывается, что это не более, чем «a piece of good luck»⁹. Иными словами, в системе Птолемея отсутствовали (на уровне теории) регулярные закономерные связи между отдельными закономерностями («regularities of regularities», как выразился З. Бехлер). Предположить же, что все наблюдаемые закономерности и взаимосвязи отдельных явлений — просто случайное совпадение, было бы абсурдно: подобных совпадений оказывалось слишком много. Коперник не мог себе представить, чтобы Творец создал мир, в коем «regularities of regularities» были просто игрой случая. Именно в несистемности «системы» Птолемея¹⁰, в ее «логической гибкости» польский астроном усматривал ее главный порок, ее «монстрообразность», а не в ее несоответствии физике Аристотеля. Установить необходимые взаимосвязи между отдельными закономерностями означало создать новую логическую форму теории, ибо — и здесь фромборкский каноник вполне схоластически традиционен — логическая форма, при прочих равных условиях, и есть критерий истины. Что же конкретно предложил Коперник в математико-астрономическом плане?

Несколько упрощенно, опуская многие (впрочем, немаловажные) детали, можно представить переход от гео- к гелиоцентрической модели так, как показано на рис. 4, а—г.¹¹ В случае верхних планет положение Солнца фиксируется в точке S (рис. 4, а), а затем стороне ST параллелограмма STNP придают вращение около этой точки, при этом стороны SP и TN также обращаются вокруг точки S, а точка N — вокруг точки P. В этой новой, гелиоцентрической, кинематической схеме (рис. 4, в) эпицикл с центром N исчезает. В случае нижних планет (рис. 4, в) преобразование столь же несложно: Солнце фиксируется в точке N, т. е. в центре эпицикла, а Земле придается вращение вокруг этого нового положения Солнца по большому кругу, планета же движется по кругу меньшего радиуса (рис. 4, г). В этом случае «лишним» оказывается деферент планеты.

Рис. 4. Переход от гео- к гелиоцентрической модели: а — геоцентрическая модель для верхних планет; б — гелиоцентрическая модель для верхних планет; в — геоцентрическая модель для нижних планет; г — гелиоцентрическая модель для нижних планет.

В теории Коперника планетные регрессии получили новое объяснение — они представляют собой некий оптический эффект, связанный с положением наблюдателя на движущейся Земле (рис. 5). Упомянутая выше «связь» движения Венеры и Меркурия с движением Солнца также получила простое объяснение (рис. 6). Таким образом, если Птолемею для объяснения упомянутых феноменов нужно было вводить непонятно откуда взявшиеся дополнительные ad hoc-гипотезы (подбирать скорости движения по эпициклу и деференту, требовать параллельности некоторых отрезков и т. д. и т. п.), то Копернику удалось многое объяснить просто благодаря «более рациональному расположению кругов». Гелиоцентрическая схема движения планет объясняла целый ряд явлений в силу иного положения наблюдателя, что в свою очередь меняло структуру каузальных связей.

Теория Коперника изменяла характер объяснений астрономических явлений. У Птолемея объяснения, скажем, планетных регрессий имели апостериорный характер, для «спасения явлений» в теорию вводились те допущения, которые никак не вытекали из ее исходных принципов. Иначе в теории Коперника, в которой и регрессии, и ограниченность углов элонгации для нижних планет, и другие явления есть необходимые следствия исходных положений его системы, и в этом смысле последняя является априорной. Это обстоятельство — кстати, немаловажное для оценки восприятия гелиоцентризма в лютеранских кругах¹² — не осталось незамеченным современниками и последователями Коперника. Так, например, голландский математик Гемма Фризий (G. Frisius; 1508—1555) писал: «Птолемей допускает, что три высших планеты восходят ахронически, т. е. диаметрально противоположно Солнцу, находясь всегда в перигее своих эпициклов; и это τὸ ότι [a posteriori]. Гипотеза же Коперника выводит эту истину как необходимую, и доказывает [ее] διότι [a priori]»¹³.

Рис. 5. К объяснению явления регрессии с позиций гелиоцентрической модели.

И еще одно существенное обстоятельство. В теории Птолемея расстояния «Земля — планета» не могли быть определены, так как в ней фигурируют лишь отношения R/r для планет. Теория же Коперника позволяла выразить расстояние каждой планеты до Солнца в единицах TS, т. е. в единицах расстояния «Солнце — Земля», которое и стало естественной мерой для определения космических пропорций¹⁴.

Тем самым, RT-симметрия получила в гелиоцентрической теории свое законченное выражение: чем дальше планета от центра вращения, тем больше ее период обращения. Тогда звездная сфера должна быть неподвижной в силу ее невероятно большой (Коперник мудро обошел вопрос о бесконечности Вселенной) удаленности от этого центра, что и заставило предположить суточное движение Земли.

Рис. 6. Углы элонгации Меркурия и Венеры в гелиоцентрической модели.

Кстати, о размерах Вселенной. Чтобы оправдать ненаблюдаемость звездного параллакса во времена, когда технические возможности дотелескопической наблюдательной астрономии были весьма ограниченны, следовало допустить, что удаленность сферы неподвижных звезд от земного наблюдателя должна составлять никак не меньше 1 500 000 земных радиусов (по расчетам Кеплера звезды удалены от Солнца на 60 миллионов земных радиусов¹⁵, Тихо Враге оценивал это расстояние в 7 850000 земных радиусов), тогда как арабские астрономы полагали (и с ними в Средние века и в начале Нового времени соглашались многие европейские), что в действительности это расстояние много меньше — ок. 20 110 земных радиусов¹⁶. Если последнее мнение справедливо, то звездный параллакс в гелиоцентрической/геодинамической теории должен быть наблюдаем, а поскольку он ненаблюдаем, то отсюда делался вывод, что теория Коперника ложна. Ненаблюдаемость звездного параллакса не была для Коперника «win — win»-ситуацией (если звездный параллакс удастся обнаружить, значит его теория верна, а если не удастся, то это не доказательство ее ложности, а свидетельство громадности расстояния от Земли до сферы неподвижных звезд), как полагают многие историки¹⁷.

Но несмотря на эти и иные трудности и несовершенства теории Коперника, Космос обрел в ней симметрию в том смысле этого слова, который в него вкладывали некоторые греческие авторы, в частности Герон Александрийский (ок. 100): «мы называем симметричными величины, кои измеримы общей стандартной мерой»¹⁸. Однако здесь следует сделать одну важную оговорку. Никакого независимого эмпирического теста на истинность полученных Коперником результатов (или результатов, которые могли быть получены из его теории) в то время не существовало, и поэтому совершенно справедливо замечание А. Петрони и Л. Сколамьеро о том, что возможность «определения планетных расстояний не относится к эмпирическим аспектам коперниканской системы. Она составляет лишь часть систематического превосходства (systematic superiority) этой системы над системой Птолемея»¹⁹.

Примечания

1. Птолемей К., 1998. С. 401.

2. То, что движения точек P и N происходят в одну и ту же сторону, не является неким обязательным условием, но это условие пришлось принять для правильного описания движения планет в данной модели.

3. «Мы полагаем, — писал Птолемей, — что для математика основной задачей является в конечном счете показать, что небесные явления получаются при помощи равномерных круговых движений» (Птолемей К., 1998. С. 82).

4. Фактически речь здесь идет о двух моделях — эпициклической (при этом считается, что Земля находится в точке O) и модели эксцентра. Но часто при описании движения планет использовались обе модели, как это показано на рис. 1 и объяснено в основном тексте.

5. Коперник Н., 1964. С. 306. — Отмеченное Коперником обстоятельство, разумеется, могло послужить толчком к созданию новой «системы мира», однако, следует иметь в виду, что для исправления указанного недостатка теории Птолемея переходить к новой, гелиоцентрической космологии не было никакой необходимости.

6. Часто термины «верхние» и «нижние» планеты используют, когда речь идет о геоцентрической теории, а термины «внешние» и «внутренние» — когда рассматривают структуру Солнечной системы с позиций гелиоцентризма.

7. Коперник Н., 1964. С. 32.

8. Аналогично, чтобы объяснить особенности движения нижних планет, Птолемею также пришлось ввести некоторые дополнительные допущения. Были и другие закономерности в планетных движениях, в частности, связанные с периодами обращения планет (подр. см.: Бронштэн В.А., 1988. С. 114—115).

9. Bechler Z., 1991. P. 83.

10. По словам Г. Хона и Б. Гольдштейна, Коперник рассматривал систему Птолемея как «a mixed bag of theories» (Hon G., Goldstein B.R., 2004. P. 276).

11. Более детализированное изложение дано в Приложении.

12. О чем см. Подр.: Barker P., 2000.

13. Frisius G., 1556. А2^r; см. также: Goldstein B., 1987.

14. Тем самым, RT-симметрия получила в гелиоцентрической теории свое законченное выражение: чем дальше планета от центра вращения, тем больше ее период обращения. Но тогда звездная сфера должна быть неподвижной в силу ее невероятно большой (Коперник мудро обошел вопрос о бесконечности Вселенной) удаленности от этого центра, что и заставило предположить суточное движение Земли.

15. Kepler J., 1953. P. 492. — Бо́льшую цифру до середины XVII в. не называл никто.

16. Goldstein B.R., 1967. P. 7; Aaboe A., 2001. P. 127—131.

17. Согласно измерениям немецкого астронома Ф.В. Бесселя (F.W. Bessel; 1784—1846), который в 1838 г. определил звездный параллакс, расстояние от Солнца до звезды 61 Cygni в созвездии Лебедя составляет ок. 715400 земных радиусов.

18. Цит. по: Hallyn F., 1993. P. 88. Можно указать и более ранние примеры подобного понимания симметрии, скажем, Канон Поликлета (V в. до н. э.), эстетика которого, по мнению Э. Панофского, близка ренессансной.

19. Petroni A.M., Scalamiero L., 1986. P. 339.