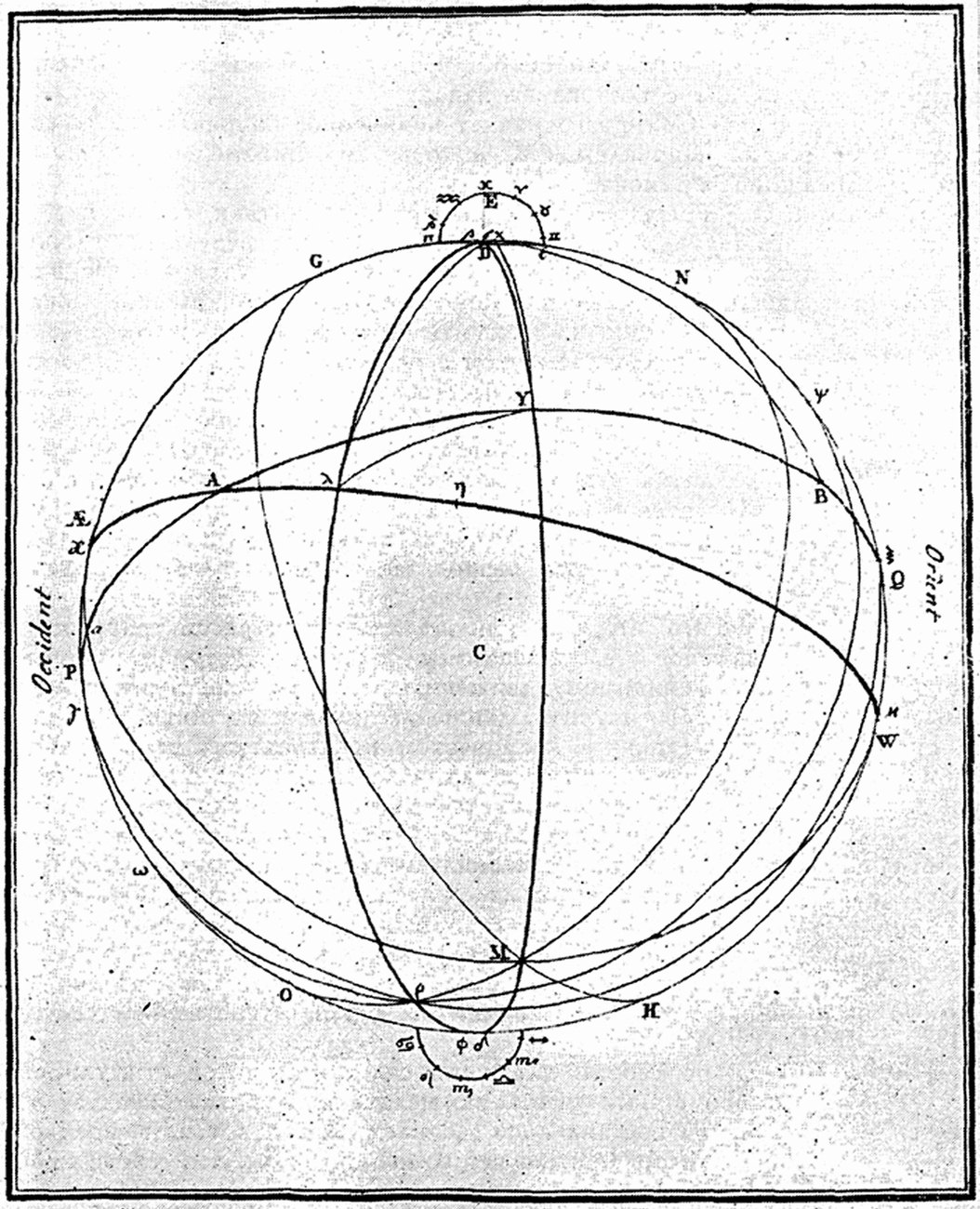
Теория движения солнечных пятен

Предложенная Делилем теория движения солнечных пятен основывалась на его собственных наблюдениях, проведенных в мае 1713 г. Заметив 19 мая большое пятно на диске Солнца, Делиль определил его гелиоцентрические координаты α и δ с помощью 7-футовой трубы, установленной на параллактической машине и снабженной сетью из 4 нитей, наклоненных друг к другу под углом в 45°. Наблюдения продолжались до 29 мая, пока пятно не исчезло. Теория была разработана им вскоре после наблюдений, но, как говорилось выше, она еще долгие годы оставалась в рукописи.

С 15 июля по 16 октября 1734 г. аналогичные наблюдения удалось провести и в Петербургской обсерватории.¹ В них участвовали Делиль, Винсгейм и Эйлер. Полюбоваться столь редким в те годы явлением, вероятно, приходили многие стажеры обсерватории и сотрудники Академии. В их числе, возможно, был и Крафт, который 17 января 1735 г. представил Конференции заметку на латинском языке о солнечных пятнах [49, т. 1, с. 137]. Ее русский перевод в том же году был опубликован в журнале «Примечания на ведомости» [139, 1735 г., ч. 23—27].

27 января 1735 г. Крафт представил диссертацию «Об определении расстояний солнечных пятен» [49, т. 1, с. 141]. Тщательно изучив работу и обсудив ее с автором, Делиль вернул ее 7 февраля того же года, сделав несколько исправлений и замечаний [49, т. 1, с. 146, 150]. Крафт письменно ответил на замечания. Дальнейшая судьба этой работы неизвестна. Однако, судя по названию, Крафт был хорошо знаком с теорией Делиля о движении солнечных пятен, положения которой он использовал в своей диссертации.

Как можно судить по заметкам в записных книжках Эйлера,² в 1734—1735 гг. он также живо интересовался теорией Делиля и по-своему решал задачу определения расстояний солнечных пятен от краев диска Солнца. Однако и его результаты не были опубликованы при жизни Делиля. Лишь в 1768 г. за подписью старшего сына Эйлера Иоганна Альбрехта была опубликована статья «О вращении Солнца вокруг оси, определенном по видимому движению пятен» [12, с. 386]. Эта работа подвела итоги многолетним исследованиям, начатым Делилем в 1713 г. в Париже и продолженным затем в Петербурге.

С чего же они начинались? Как отмечалось выше, впервые «Теория движения солнечных пятен» Делиля была опубликована в Петербурге в 1738 г. [132, с. 143—179]. С помощью построения чертежей, представлявших собой различные проекции Солнца на плоскость эклиптики, Делиль определял видимый путь пятна по диску Солнца с первого до последнего дня его появления. Если пятно удавалось наблюдать несколько дней подряд, измерялся период вращения Солнца вокруг своей оси, наклон оси к плоскости эклиптики, скорость осевого вращения и т. п.

Говоря об особенностях своей теории, Делиль писал: «Теория, которую я здесь излагаю, состоит в объяснении фигур, которые тут приложены. Решение всех задач, которые могут быть предложены о движении солнечных пятен, будут найдены геометрически и арифметически...» [132, с. 143].

Один из чертежей Делиля к его статье: «Теория движения солнечных пятен».

Теория строилась на следующих 3 предположениях:

1) Солнце завершает один оборот вокруг своей оси за 25.5 дней, его вращение происходит с востока на запад;

2) ось вращения Солнца сохраняет неизменное направление: ее северный полюс всегда направлен к 8° в созвездии Близнецов, а южный — к 8° в созвездии Скорпиона;

3) наклон оси вращения Солнца к оси эклиптики составляет 7.5°.

Видимое движение пятна рассматривалось как результат сложения двух действительных движений: осевого вращения Солнца и годичного движения солнечной оси относительно оси эклиптики. Делиль показал, что движение пятна должно происходить по эллиптической циклоиде. Его метод состоял в построении циклоиды и позволял получить столько точек этой кривой, сколько было сделано наблюдений каждого пятна [132, с. 146]. В статье предлагался также и метод вычисления периода осевого вращения Солнца по 3 наблюдениям прямого восхождения и склонения одного и того же пятна. Разнообразные задачи о движении солнечных пятен Делиль решал в своей статье лишь с помощью парижских наблюдений, пообещав позднее использовать и новые материалы, полученные в Петербурге. Как отмечалось выше, это было сделано Крафтом и Эйлером.

Интересно отметить, что в теории Делиля пятно рассматривалось как своеобразное «небесное тело», видимое движение которого по диску Солнца уподоблялось видимому движению реальных планет или комет по небесной сфере. Чтобы изучить движение солнечного пятна, следовало вычислить его траекторию в космическом пространстве, т. е. «орбиту». Виртуозно владея сложнейшими методами проективной геометрии, Делиль все же отлично понимал непригодность своего метода для широкого практического применения. Он призвал петербургских ученых взяться за разработку более простых и удобных аналитических методов. Делиль писал: «Метод, который я только что предложил для нахождения видимого расстояния... между центром Солнца и пятном по наблюдениям прямого восхождения и склонения, в принципе точен. Но следовало бы заменить его другим, значительно более удобным, в котором ошибка в величине видимого расстояния... не превосходила бы одной единственной секунды» [132, с. 169].

Работа Делиля по теории движения солнечных пятен стимулировала исследования петербургских ученых по механике и математике. Как отмечалось выше, решения поставленной Делилем задачи в 1735 г. предложил Крафт и в 1768 г. Эйлер. Однако нет сомнения в том, что с этой проблемой уже с самого первого своего появления в обсерватории знакомились все стажеры, и прежде всего те, кто участвовал в наблюдениях Солнца. Например, Бернулли вел такие наблюдения в 1728 г. (см. гл. 2), а с 1729 г. начал работать над своей «Гидродинамикой».

Как видно из записных книжек Эйлера, в первые годы пребывания в Петербурге он усиленно занимался различными вопросами механики, алгебры и сферической тригонометрии. В эти годы, наряду с пометками по астрономии, появляются наброски планов по механике и универсальной арифметике, а затем и теории движения солнечных пятен.³ Таким образом, решение астрономических задач способствовало разработке различных проблем математики и механики.

Лист из записной книжки Эйлера с заметками по небесной механике.

Увлечение проблемами математики и механики стало в Петербурге хорошей традицией. Ей следовали все. Даже А.Д. Кантемир и Ф. Прокопович начали работать над сочинениями по алгебре, а в библиотеках петербургских ученых и тех, кто с ними сотрудничал, появилось множество книг по этим наукам. Наиболее показательна библиотека Кантемира, опись которой была составлена вскоре после смерти владельца довольно грамотными людьми. Из 847 книг и рукописей 27 — математические, в том числе 17 — по алгебре! Среди прочих книг была описана и его собственная «рукопись по алгебре... на русском языке, не переплетенная ин-4°» [111, ч. 1, с. 42].

Глубокое изучение математики, и особенно алгебры, было обязательным пунктом программы подготовки петербургских астрономов. Эту школу прошел и Ломоносов. Не случайно, что, сообщая в Петербург о ходе своего обучения за границей, он не забывал и о занятиях алгеброй. 5/16 ноября 1740 г. он писал из Марбурга: «Теперь я... упражняюсь в алгебре, намереваясь приложить ее к химии и физике мельчайших частиц» [7, т. 1, с. 545].

В первые годы работы в Петербурге, проходя стажировку в обсерватории, Ломоносов очень увлекся математикой. Увлечение Ломоносова нашло отражение в его первых сочинениях, содержащих много ярких высказываний о значении математики и ее роли в разработке естественно-научных проблем.

Так, в «276 заметках по физике и корпускулярной философии» (1741—1743 гг.) появился известный афоризм: «Химия есть правая рука физики, математика — глаза...» [7, т. 1, с. 115]. В работе «Элементы математической химии» (1741 г.) Ломоносов писал: «...кто хочет глубже постигнуть химические истины, тому необходимо изучать механику... знание механики предполагает знание чистой математики...» [7, т. 1, с. 75]. И дальше, отметив важную роль математики в формировании гидравлики, аэрометрии, оптики и других наук, он добавлял: «...все, что до того было в этих науках темно, сомнительно и недостоверно, математика сделала ясным, достоверным и очевидным» [7, т. 1, с. 75].

Н.И. Попов также с ученических лет проявлял живой интерес к математике, причем не ослабевший с годами. Его успехи в алгебре особо отмечал Эйлер. Впоследствии Попов переводил на русский язык «Руководство к арифметике...» (1738—1740 гг.) Эйлера и редактировал первый русский учебник по алгебре Н.Е. Муравьева, опубликованный в 1752 г. [73, с. 57, 58].

Неудивительно, что при таком культе математики чье-либо пренебрежение к этой науке вызывало у петербургских ученых дружное осуждение. Зная это, Шумахер в очередной раз решил воспользоваться случаем, чтобы, следуя своему правилу, помешать продвижению отечественных ученых. Он отправил на отзыв к Эйлеру, находившемуся тогда в Берлине, (рукопись первых трудов Рихмана по испарению жидкостей, теплофизике и электричеству. В сопроводительном письме от 21 июля/1 августа 1744 г. Шумахер не преминул сообщить знаменитому математику о том, что Рихман не желает заниматься математикой, так как уверен в том, что «...он мог бы стать великим физиком и без знания вычислений» [64, т. 2, с. 69].

Грозный правитель Академической канцелярии ни минуты не сомневался в том, что это сообщение вызовет у Эйлера неприязнь к Рихману и заставит его дать отрицательный отзыв на присланные рукописи. Интересно отметить, что с той же целью Шумахер посылал на отзыв Эйлеру и рукописи Ломоносова, которого нельзя было заподозрить в неуважении к математике. Тогда Шумахер выбрал для рецензирования такую рукопись Ломоносова, где резко критиковались взгляды Эйлера на строение земной атмосферы (см. гл. 5). Однако Эйлер сумел разгадать коварный замысел Шумахера и не попался в расставленную западню. О работах Рихмана он дал восторженный отзыв, не забыв отметить его «весьма значительные успехи в физике и математике» [64, т. 2, с. 106]. Знаменательно, что и свой отзыв Эйлер послал не Шумахеру, а новому президенту Академии К.Г. Разумовскому в двух письмах — от 7/18 и 10/21 ноября 1747 г. [64, т. 2, с. 105—108].

Хорошая математическая подготовка и участие в работе обсерватории и Географического департамента были надежной основой для приобщения всех штатных и добровольных сотрудников Делиля к исследованиям по небесной механике и эфемеридной астрономии. Начало этим работам положили наблюдения Солнца, в которых с удовольствием участвовали все стажеры. Первые такие наблюдения и работы выполнил Майер, весьма талантливый, но, к сожалению, рано умерший ученый. Он активно помогал Делилю в составлении солнечных таблиц, провел их сравнение с таблицами, которые были составлены по наблюдениям Гевелия. Доклад на эту тему Майер сделал в Академии 31 января 1727 г. [49, т. 1, с. 9]. В дальнейшем он неоднократно возвращался к разработке различных методов определения моментов солнцестояний, равноденствий и стояний планет [49, т. 1, с. 17, 18, 20, 99, 100 и др.]. Это дало ему повод значительно усовершенствовать аналитическую трактовку тригонометрии, к чему призывал Делиль, и решить ряд сложных задач сферической тригонометрии.

Наблюдениями солнцестояний и равноденствий много занимался и Крафт. 6 ноября 1730 г. он делал в Академии доклад на тему: «Наблюдения летнего солнцестояния 1730 г.», в котором изложил: 1) историю вопроса, 2) сравнительные методы меридианных наблюдений, принятые прежними и современными ему астрономами и состоявшие в наблюдениях, выполненных в камере-обскуре; 3) предложил новый способ для вычисления момента солнцестояния по данным каких-либо полуденных высот Солнца [49, т. 1, с. 31].

Предложенный Майером метод обозначения тригонометрических функций использовали Крафт, Герман, Бернулли и другие петербургские ученые [170]. Позднее ту же аналитическую трактовку тригонометрических формул применял и Мопертюи в своей «Мореходной астрономии» [171]. Эйлер значительно усовершенствовал математическую символику в разных областях анализа, сферической тригонометрии и т. д. В трудах великого математика эти разделы приобрели классическую, известную в настоящее время форму.

По мере создания удобных аналитических методов Эйлер применял их к решению все новых и новых задач, связанных с движением небесных тел, которые ставили перед ним Делиль и другие наблюдатели. Как известно, Эйлер стал одним из основателей новой науки, базирующейся на учении Ньютона, и получил фундаментальные результаты в самых разных ее отраслях. Интересно отметить, что в 50-е годы XVIII в. он даже предлагал название для этой науки — «астрономическая механика» [12, с. 84]. Однако оно не удержалось в научной терминологии и позднее было заменено названием, предложенным Лапласом, «небесная механика», употребляемым и поныне.

Нет необходимости подробнее останавливаться здесь на классических трудах Эйлера по небесной механике. В настоящее время они хорошо изучены [62 и др.] и широко известны. Напомним лишь, что этими исследованиями он начал заниматься с первых дней своего пребывания в Петербурге. Как видно из пометок в записных книжках ученого, он был привлечен Делилем к решению многих задач, связанных с вычислением движения Луны, планет и комет. Так, например, он размышлял над сформулированной Гольдбахом проблемой нахождения алгебраической кривой, по которой движется Луна, искал лучший метод составления астрономических таблиц геоцентрических мест планет и т. д.⁴

Разработка теории движения Луны, включенная Делилем в программу научных исследований Петербургской обсерватории, так же как и создание теории приливов и отливов имели важное практическое значение для обеспечения нужд морского флота. Делиль, Герман, Бернулли, Эйлер, Майер, а позднее Попов, Курганов и другие астрономы много занимались этими вопросами. При решении различных проблем небесной механики петербургские ученые широко пользовались данными астрономических, метеорологических и геофизических наблюдений, полученных в Академической обсерватории, особенно за первое 20-летие ее деятельности.

Интересный пример такого использования наблюдений можно найти в статье «О приливе и отливе», опубликованной в журнале «Примечания на ведомости». В ней Крафт подробно рассмотрел гипотезы Ньютона и Декарта, объясняющие возникновение прилива и отлива — за счет притяжения Луны и за счет «давления лунного вихря». Решительно встав на сторону Ньютона, Крафт так обосновывал несостоятельность гипотезы о действии «лунного вихря»: «...надлежало бы оного действие такожде и на ртуте в барометрах приметить, от которого оная знатно выше подымалась бы, но сие не примечено» [139, 1729, ч. 89, с. 363]. Таков был первый шаг петербургских астрономов в борьбе с отжившими свой век «вихревыми» представлениями, за утверждение нового естествознания, основанного на учении Коперника — Кеплера — Ньютона. Следующим важным этапом стали работы по теории движения комет.

Примечания

1. ЛО А АН СССР, Р. 1, оп. 44, № 1, л. 342—378.

2. Там же, ф. 136, оп. 1, № 131, л. 64 об.

3. Там же, № 130, л. 52 об., 57; № 131, л. 64 об.

4. Там же, № 131. л. 124—135, 64 об. — 66 и др.