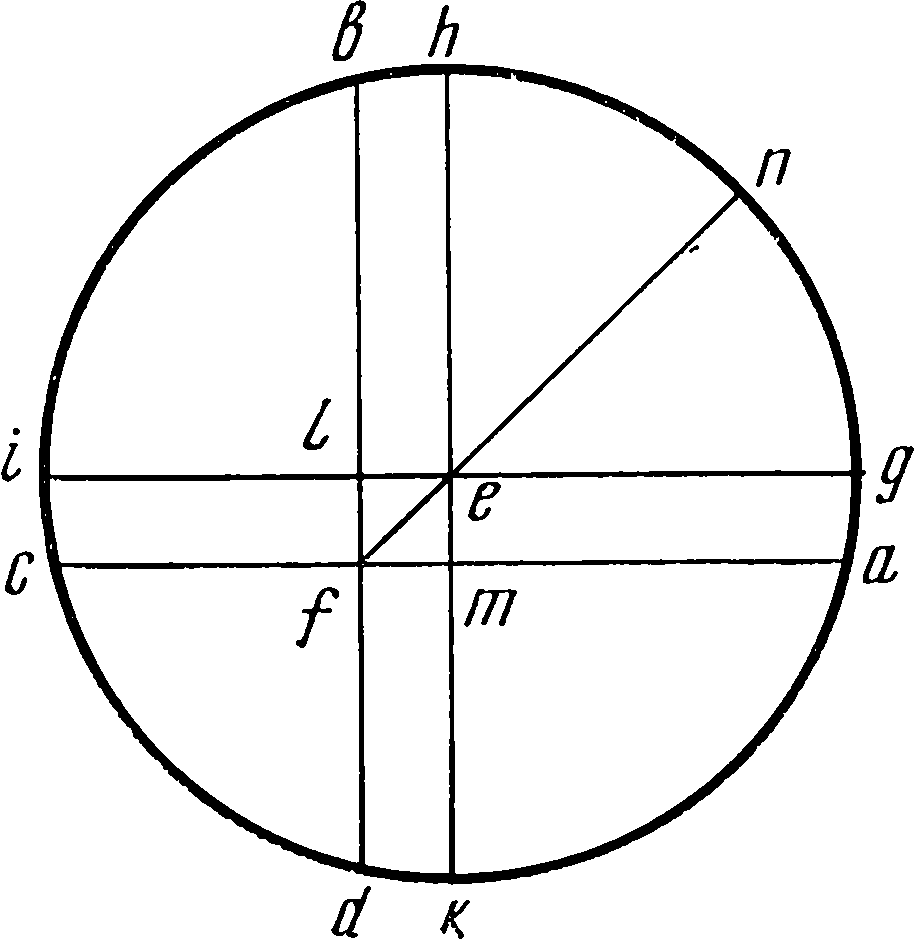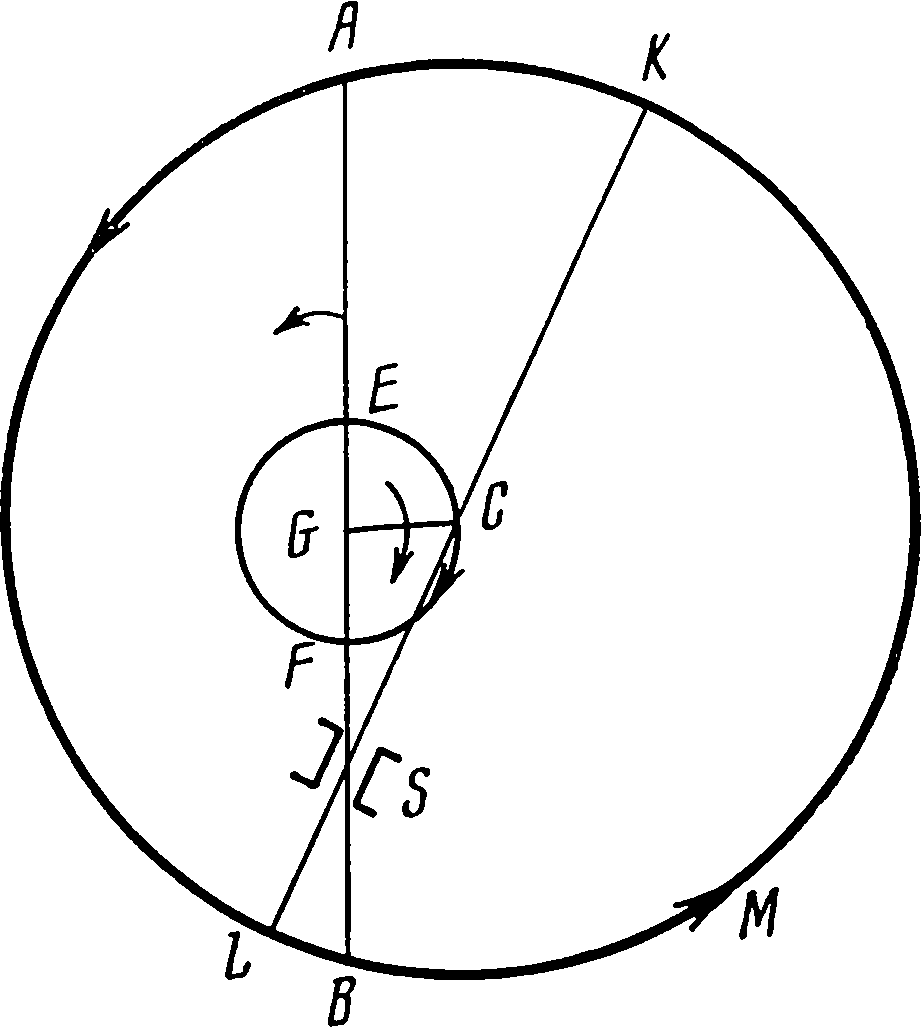Материалы по истории астрономии
| |
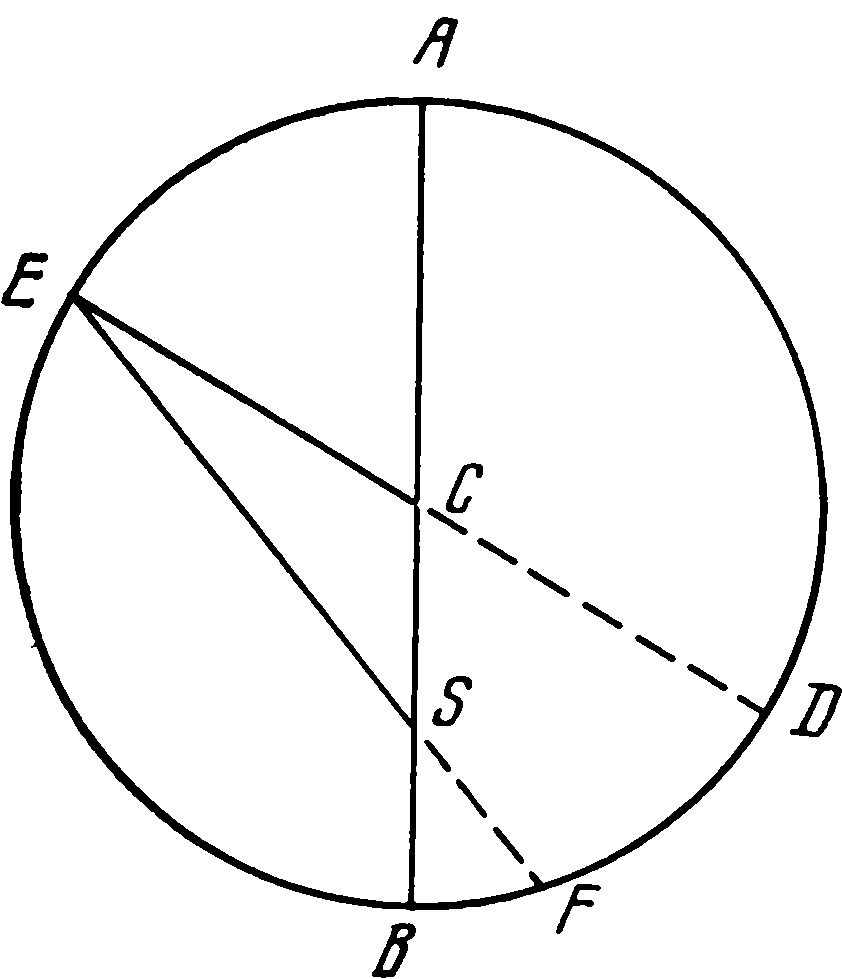
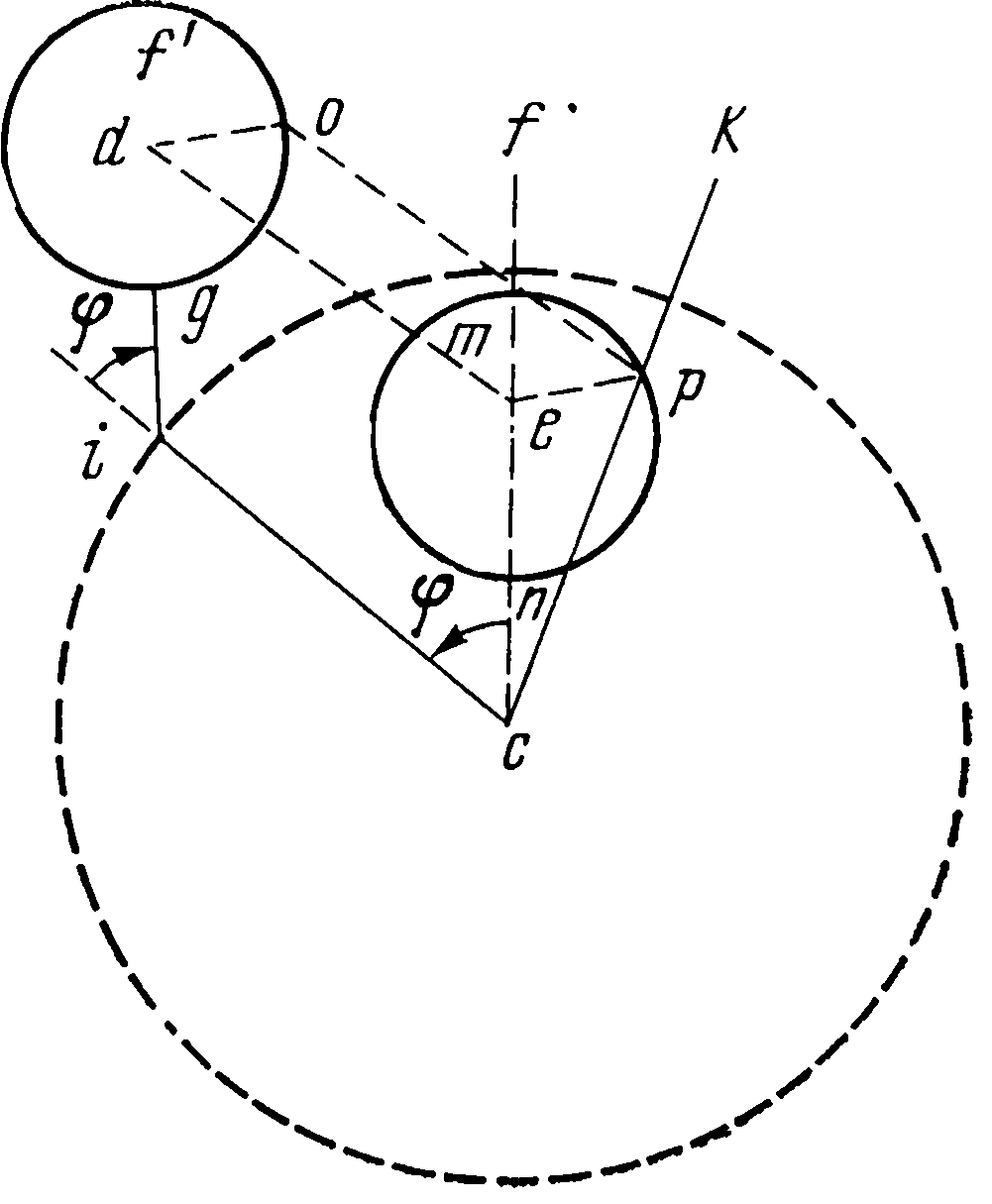
15. Теория видимого движения СолнцаКак уже отмечалось, 1520-е годы были весьма плодотворными в научной деятельности Коперника: к этому периоду относятся его экономические работы, в эти же годы была практически завершена разработка гелиоцентрической теории, изложенная в рукописи «О вращениях небесных сфер». Важное место этой рукописи составляет ее третья книга, которую можно считать отправной точкой всей астрономической теории Коперника. Поэтому когда Ретик познакомился с рукописью «Вращений» и решил опубликовать ее, начал он именно с третьей книги. Уже первые строки этого раздела отвечают на вопрос о том, с какими целями производил свои исследования Коперник. «Древние математики не отличали тропического, или естественного, года, который отсчитывается от равноденствия или солнцестояния, от года, который определяется по отношению к какой-нибудь из неподвижных звезд. Но Гиппарх Родосский, муж удивительной остроты ума, первый заметил, что они отличаются друг от друга... он нашел, что год, отнесенный к неподвижным звездам, больше года, отнесенного к равноденствиям... Поэтому он предположил, что и неподвижные звезды имеют некоторое движение в направлении последовательности знаков, но очень медленное и не сразу заметное. Однако с течением времени оно обнаружилось уже совершенно ясно, так что восход и заход знаков зодиака и звезд мы видим значительно отличающимися от предсказанных древними... Кроме того, само это движение оказывается неравномерным. Желающие объяснить причины этой неравномерности приводили различные мнения. Одни полагали, что у висящего в пространстве мира есть некоторое колебательное движение... Когда соответствующее перемещение дойдет... до некоторого предела, то оно... должно... пойти обратно, причем наибольшее отклонение ...от среднего положения составляет не более 8 градусов. Но... выяснилось, что голова созвездия Овна более чем на трижды восемь градусов отошла от точки весеннего равноденствия, равно как и другие звезды, причем в течение стольких веков не было замечено ни малейшего следа возвращения назад. Другие высказывали мнение, что сфера неподвижных звезд движется вперед, но неравномерно... К этому присоединилось еще другое удивительное явление природы, что наклонность зодиака не представляется нам такой по величине, какой она была до Птолемея... Для объяснения этого... придумали девятую и даже десятую сферу, которые, по их мнению, производили это, однако и так они не смогли добиться, чего хотели. Уже начала появляться на свет даже одиннадцатая сфера; это число кругов, как излишнее, мы легко опровергнем движением Земли... Равноденствия и солнцевороты кажутся наступающими несколько раньше не потому, что в направлении последовательности знаков движется сфера неподвижных звезд, а скорее потому, что против последовательности знаков движется равноденственный круг, стоящий наклонно к плоскости зодиака в соответствии с мерой отклонения оси земного шара. Ведь гораздо сообразнее сказать, что равноденственный круг стоит наклонно к зодиаку, чем зодиак к равноденственному, как меньший по отношению к большему»1. В следующей II главе третьей книги Коперник излагает исходные данные, легшие в основу его работы. «В первом из 76-летних периодов Калиппа, в 36-м году его, т. е. в 30-м году после смерти Александра Великого, александриец Тимохар... указал, что Колос, который держит Дева (α Virginis. — Авт.), отстоял от точки солнцестояния на 82 градуса с третью, имея южную широту 2 градуса, а звезда во лбу Скорпиона, самая северная из трех (β Scorpii. — Авт.) ...имела широту 1 градус с третью, а долготу 32 градуса от осеннего равноденствия. ...В 48-м году того же периода он нашел, что Колос Девы отстоит по долготе на 82½ градуса от точки летнего солнцестояния при той же самой широте. А Гиппарх в 50 году третьего Калиппова периода, или в 196-м году по смерти Александра, нашел, что звезда в груди Льва, называемая Регулом (а Leonis. — Авт.), следует за летним солнцестоянием на расстоянии 29½ и одной трети градуса. Далее Менелай, римский геометр, в первом году правления Траяна, т. е. в 99-м от P. X. и 422-м по смерти Александра, указал, что Колос Девы отстоит по долготе от солнцестояния на 86 градусов с четвертью, а звезда во лбу Скорпиона — на 36 градусов без двенадцатой части от осеннего равноденствия. Следом за ними Птолемей... во втором году Антонина Пия, т. е. в 462-м после смерти Александра, определил, что Регул Льва отстоит на 32½ градуса от «летнего» солнцестояния, Колос — на 86½ градуса, а упомянутая звезда во лбу Скорпиона — на 36 с третью градуса долготы от осеннего равноденствия при совершенно неизменной широте. ...На 1202-м году после кончины Александра последовало наблюдение Альбатегния... Оказалось, что в этом году Регул... дошел до 44 градусов 5 минут от солнцестояния, а звезда во лбу Скорпиона — до 47 градусов 50 минут от осеннего равноденствия, причем у всех них широта осталась той же самой... ...Мы в 1525-м году от рождества Христова... который был 1849-м египетским годом после смерти Александра, наблюдали Спику во Фрауэнбурге в Пруссии, и наибольшая ее высота по меридианному кругу оказалась приблизительно 27 градусов. Широту места наблюдения мы нашли равной 54 градусам 19½ минуты. На основании этого склонение ее по отношению к равноденственному кругу определилось равным 8 градусам 40 минутам»2. На основании этого Коперник определяет долготу звезды Спики; любопытно, что он делает это без сферической тригонометрии. Полученное им положение Спики «17 градусов 21 минута от начала Весов»... Перерасчет по таблицам пятизначных логарифмов дает долготу Спики 180°+17°21′. «За десять лет перед этим, в 1515 году, мы нашли ее склонение равным 8 градусам 36 минутам, а положение на 17 градусах 14 минутах Весов. Птолемей же писал, что ее склонение равно по меньшей мере половине одного градуса. Следовательно, ее положение было на 26 градусах 40 минутах Девы, что представляется более истинным по сравнению с предшествующими наблюдениями (86½ градуса — 60° = 26°30′. — Авт.)»3. Основной фактический материал был взят Коперником из второй главы VII книги Птолемея. Установленные Калиппом циклы в 76 = 4×19 лет имели отправной точкой 329-й год до н. э. «Отсюда... видно, что... за все время от Тимохара до Птолемея, а именно за 432 года, точки равноденствий... перемещались прецессионным движением большей частью на один градус в сто лет... Для первой звезды во лбу Скорпиона наблюденное Альбатегнием положение по сравнению с менелаевым показывает, что... за... 782 года перемещение равнялось 11 градусам 55 минутам, и перемещению в один градус нужно приписать не сотню лет, а только 66, а от Птолемея за 741 год одному градусу соответствовали только 65 лет... Если остальной промежуток времени 645 лет отнести к разности 9 градусов 11 минут, по нашим наблюдениям, то один градус получит 71 год. Из этого ясно, что в течение 400 лет перед Птолемеем предварение равноденствий было более медленным, чем от Птолемея до Альбатегния, а в этот промежуток оно было более быстрым, чем от Альбатегния до нашего времени»4. Нужно, однако, заметить, что, понадеявшись на Птолемея, Коперник допустил ошибку. Внимательное чтение цитаты из Гиппарха (в конце второй главы VII книги «Альмагеста») «не менее чем на сотую часть градуса за один год» показывает, что эту наименьшую величину для прецессии Птолемей принял за действительную. Данная Птолемеем величина прецессии 36″ в год была принята всеми греческими и арабскими астрономами, и только аль-Баттани (850—929) указал впервые более точную величину прецессии. Неравномерность прецессионного движения равноденственных точек столь мала, что не могла быть обнаружена во времена Коперника. Отмеченная им мнимая неравномерность является результатом неточности наблюдений, а также большой величины промежутков между составлением отдельных каталогов. «Также замечается различие и в изменении наклонности эклиптики. Аристарх Самосский определял наклон зодиака к равноденственному кругу в 23 градуса 51 минуту 20 секунд, так же как и Птолемей, Альбатегний — в 23 градуса 36 минут, Арзахель Испанский через 190 лет после него — в 23 градуса 34 минуты, точно так же через 230 лет Профаций Иудей нашел ее меньшей почти на две минуты. В наше же время наклонность не оказывается большей 23 градусов 28½ минуты, так что и отсюда становится ясным, что самое медленное ее изменение было от Аристарха до Птолемея, а самое быстрое — от Птолемея до Альбатегния»5. Описав явление прецессии, Коперник выдвигает основную гипотезу для ее объяснения. Он отвергает возможность специального движения восьмой сферы (трепидацию), предложенную Сабитом ибн-Каррой, которого он не упоминает, а затем излагает дошедший до него материал старых наблюдений. Так как у него в то время не было армиллы, позволявшей измерять дуги во всех направлениях, он при помощи трикветрума измеряет вертикальные дуги и потом пересчитывает их, чтобы найти величину дуги на эклиптике. Затем определяет общий характер соответствующего изменения интересующих его величин. Прецессионное движение Коперник разлагает на среднее равномерное, его неравенство описывает при помощи колебательного движения, совершающегося по эклиптике, а изменение наклона эклиптики — при помощи колебательного движения по направлению, перпендикулярному к эклиптике. В современной астрономии прецессионное движение Земли разлагается на два — прецессию — заставляющую ось Земли описывать конус около оси, перпендикулярной к эклиптике, и нутацию — изменяющую угол при вершине конуса, заключающийся между осью и образующей конуса. Прецессионное движение (у Коперника — равномерное движение среднего полюса) определено сейчас достаточно точно: 50,20″ в год (вместо 50,26″ у Коперника или 50,17″ для его времени). Что же касается данных Коперника по отклонениям от среднего полюса — двух колебательных движений (либраций) с периодами в 1717 и 3434 лет, то они совершенно не соответствуют действительности: период нутации составляет всего около 19 лет, и отклонения слишком незначительны (максимум 9,2″), чтобы их можно было заметить в эпоху Коперника (нутация была открыта лишь в XVIII в. английским астрономом Брадлеем). Эта теория Коперника (изложенная им в гл. III—V) хотя и оказалась неверной, для современного читателя, несомненно, представляет математический, а также исторический интерес. Отметим прежде всего, что кроме Альбатегния (аль-Баттани) он упоминает еще Арзахеля (аз-Заркали — автор толедских таблиц и сторонник теории гомоцентрических сфер) и некоего Профация Иудея. Это провансальский астроном Якоб бен-Мехир, рукописный альманах которого на 1302 г. находился в библиотеке г. Бранево, недалеко от Фромборка, и был доступен Копернику. Мы можем сказать, что для своей теории Коперник использовал материалы всех доступных ему авторов, которых он и упомянул. На это приходится обратить особое внимание, так как в последнее время некоторые коперниковеды стали приписывать ему знакомство с рядом арабских авторов, которых он не называет. В IV главе Коперник указывает, каким образом колебательное движение по прямой линии составляется из круговых. Это тот самый процесс, при помощи которого Евдокс Книдский объяснял прямые и обратные движения планет. В своей книге «Точные науки в древности» О. Нейгебауэр, рассматривая движение Меркурия, указывает, что прямолинейное колебательное движение Коперник получает «при помощи способа ат-Туси», знаменитого директора Марагской обсерватории Насирэддина (1201—1274), хорошо известного специалистам по неевклидовой геометрии, при этом Нейгебауэр задается вопросом: «Я не знаю, через посредство кого Коперник узнал о конструкции Туси»6. Более уместен был бы вопрос, через посредство кого Туси узнал о конструкции Евдокса. Кроме того, нужно отметить, что у Коперника вся конструкция (с чертежом) изложена в IV главе третьей книги задолго до написания им теории движения Меркурия. В III главе Коперник разбирает задачу сложения двух взаимно перпендикулярных гармонических колебаний, у одного из которых период вдвое больше, чем у другого. Полученная им «восьмерка» является одной из фигур Лиссажу, получающихся при сложении гармонических колебаний, совершающихся по прямым, образующим между собой некоторый угол. Уравнения полученной «восьмерки» будут x = a sin 2kt, y = 2a coskt. Следующие главы (от VI до XIV) Коперник посвящает практической разработке своей теории и составлению таблиц. В этих таблицах он определяет перемещение Солнца от движущейся точки весеннего равноденствия, необходимое для вычисления движения в тропических годах. Для этого к перемещению за египетский год — 365 дней — по отношению к неподвижным звездам (первые две таблицы) прибавляется величина за то же время прецессионного движения. Величина прецессии прибавляется потому, что точка отсчета — прежнее положение точки весеннего равноденствия — перемещается против последовательности знаков зодиака, тогда как собственное движение Солнца по небесной сфере идет в направлении последовательности знаков (две последние таблицы составного равномерного движения). Затем для определения видимого движения Солнца к этому среднему движению прибавляются так называемые уравнения, которые получаются вследствие существующих неравномерностей движения Солнца. Одно из этих уравнений, впервые замеченное Гиппархом, происходит оттого, что предполагаемое равномерным движение Солнца наблюдается не из центра его траектории, а из некоторой другой геометрической точки. Гиппарх и повторяющий его рассуждения Птолемей нашли, что от весеннего равноденствия до солнцестояния проходит 94½ дня, а от солнцестояния до осеннего равноденствия 92½ дня; соответствующие средние равномерные движения для этих промежутков будут 93°9′ и 91°10′. Пусть abcd будет годовой круг движения Земли; из точки a наблюдается весеннее равноденствие, из b — летнее солнцестояние, из c — осеннее равноденствие, а из d — зимнее солнцестояние. Пусть f представляет Солнце; дуга ab = 93°9′, bc = 91°10′. Соединительные прямые ac и bd пересекаются в Солнце f. Так как abc более полукруга и ad>bc, то центр круга e должен лежать между af и bf, а апогей (наибольшее расстояние fn) будет в точке n между весенним равноденствием и летним солнцеворотом. Проводя через e прямую hek∥bd и gef∥ac, из прямоугольника emfl можем найти эксцентриситет ef и угол hen, определяющий положение апогея. Оказалось, что прямая ef составляет 1/24 радиуса en, а дуга nh равна 24½ градуса. Такую же величину нашел и Птолемей, откуда появилось мнение о неподвижности точки апогея, имеющееся в «Малом комментарии» Коперника. Но аль-Баттани нашел, что nh равно 7 градусам 43 минутам. Значит, апогей перемещается, а у Птолемея он неподвижен, поэтому некоторые астрономы (Деламбр) обвинили его в неумении наблюдать, так как он по сравнению с Гиппархом допустил ошибку примерно в 5 градусов. Однако, если учесть, что данные определены в днях, нетрудно видеть, что точность полученных величин очень мала, и если Гиппарх получил величину, близкую к действительной, то это произошло случайно, а не оттого, что Птолемей не умел наблюдать. Соответствующее наблюдение было произведено Коперником в 1515 г. Он нашел, что от весеннего равноденствия до осеннего проходит «186 дней и 5½ шестидесятых». Он пишет: «Чтобы менее ошибиться в определении равноденствий (некоторые действительно подозревают, что с более ранними наблюдателями это и случилось), мы в этом исследовании кроме равноденствий добавили и некоторые другие положения Солнца, не так уже трудные для наблюдений, а именно в серединах знаков Тельца, Льва, Скорпиона и Водолея»7. В результате он получил, что эксцентриситет составляет примерно 1/31 часть радиуса, а точка n апогея лежит не справа от h, а влево на расстоянии hn = 6⅔ градуса. Это, в частности, является доказательством того, что «Малый комментарий» написан в 1516 г. Интересно сравнить величину эксцентриситета, найденную Коперником, с современной. Известно, что с точностью до ε² кеплерово движение по эллипсу можно представить равномерным угловым движением вокруг второго фокуса. В таком случае под эксцентриситетом нужно понимать расстояние между обоими фокусами, равное удвоенному эксцентриситету в обычном смысле. Тогда найденный Коперником эксцентриситет будет соответствовать обычному ε = 1/62 = 0,010614, что близко к современному значению 0,01691 (для 1,525 г.) Соответствующее уравнение в современной астрономии называется уравнением центра. Пусть E представляет Землю, равномерно движущуюся по эклиптике с центром в C, а S — эксцентрично расположенное Солнце. При наблюдении из E видимое положение Солнца будет F, а среднее равномерно движущееся Солнце должно было бы быть в точке D. Дуга BD дает среднюю долготу Солнца, а BF — истинную долготу Солнца. Их разность, т. е. CES, называется уравнением центра. Она будет иметь наибольшую величину, когда ES перпендикулярна к AB. Эту величину Птолемей нашел равной 2 градуса, 23 минуты, а Коперник 1 градус 51 минута (современное значение 1 градус 55 минут). То обстоятельство, что точка апогея не остается неподвижной, вводит еще одно неравенство в движение Солнца. Коперник пишет: «Я... должен признаться, что нигде не встречается больших трудностей, как при определении солнечного апогея, когда нам приходится вычислять большие величины через малые и еле заметные... Посередине между апсидами одна минута может соответствовать изменению на 5 или 6 градусов, и даже небольшая неточность может привести к большой ошибке. Поэтому, поместив апогей на 6 градусах с половиной и третью градуса в знаке Рака, мы не удовлетворились бы слепым доверием к астрономическим инструментам, если бы нас не удостоверили в этом лунные и солнечные затмения. Они без малейшего сомнения обнаруживают всякую ошибку, которая могла бы в них скрываться»8. Объяснение этого второго неравенства Коперник произвел двумя способами. Первый из них заключается в следующем. Пусть KLM представляет круговую орбиту Земли. Центр C этой орбиты, двигаясь в направлении, противоположном движению Земли, описывает небольшую окружность EF вокруг неподвижного центра G, находящегося на одном и том же расстоянии от Солнца S. Во время движения С линия апсид орбиты Земли будет совершать колебания вокруг своего среднего положения AGSB, а эксцентриситет земной орбиты SC будет изменяться от наибольшего до наименьшего значений — SE и SF. При этом сама линия AGB будет медленно вращаться вокруг Солнца в том же направлении, что и Земля, т. е. в направлении последовательности знаков зодиака. Второй метод настолько остроумен и изящен, что его можно оценить в полной мере, только построив соответствующий кинематический механизм. Вокруг неподвижного центра c вращается стержень ci, угол поворота fci = φ. По отношению к ci с такой же угловой скоростью вращается другой стержень igd, который заканчивается жестко соединенным с ним кругом f′g (второй эпицикл Коперника); угол поворота этого стержня по отношению к ci будет тоже ф, но уже в противоположную сторону. Полученная «пара вращений» заставит стержень igd вместе с прикрепленным к нему эпициклом fg совершать круговое поступательное движение. Точка i описывает окружность с центром c, а точка d — окружность с центром e. Если на окружности эпицикла fg возьмем произвольную точку o, то она будет описывать окружность радиуса op = ic вокруг центра p. Если точку o перемещать по окружности второго эпицикла, то центры соответствующих окружностей будут двигаться по окружности mpn. Прямая cf, аналогичная прямой AB (см. рис. на стр. 291), может медленно вращаться вокруг точки с; она представляет среднее положение линий апсид cpk, а отрезок cp — эксцентриситет — будет изменяться между значениями cn и cm. Прямая ck соответствует прямой KL, точка c — точке S. Оба механизма производят одно и то же движение. Так как дело идет о видимом движении Солнца, то оба способа могут вполне заменять друг друга. Угол fcp (или ASK, рис. на стр. 291) носит название уравнения апогея. Движение Солнца определяется так. Сначала устанавливается положение апогея, его движение состоит из двух частей: перемещения среднего апогея и колебания около него (уравнение апогея, или второе неравенство Коперника). Затем берется простое движение Солнца (по отношению к неподвижным звездам), к которому прибавляется уравнение центра (первое неравенство Коперника). Зная положение апогея и расстояние Солнца от апогея, можно найти положение Солнца по отношению к неподвижным звездам. Примечания1. Николай Коперник. О вращениях..., стр. 158—159. 2. Николай Коперник. О вращениях..., стр. 160. 3. Там же, стр. 161—162. 4. Николай Коперник. О вращениях..., стр. 162. 5. Там же. 6. О. Нейгебауэр. Точные науки в древности. М., «Наука», 1968, стр. 196. 7. Николай Коперник. О вращениях..., стр. 205. 8. Николай Коперник. О вращениях..., стр. 211.
|
© 2002—2025 Юрий Гирин подборка материалов
«Кабинетъ» — История астрономии. Все права на тексты книг принадлежат их авторам!
При копировании материалов проекта обязательно ставить ссылку