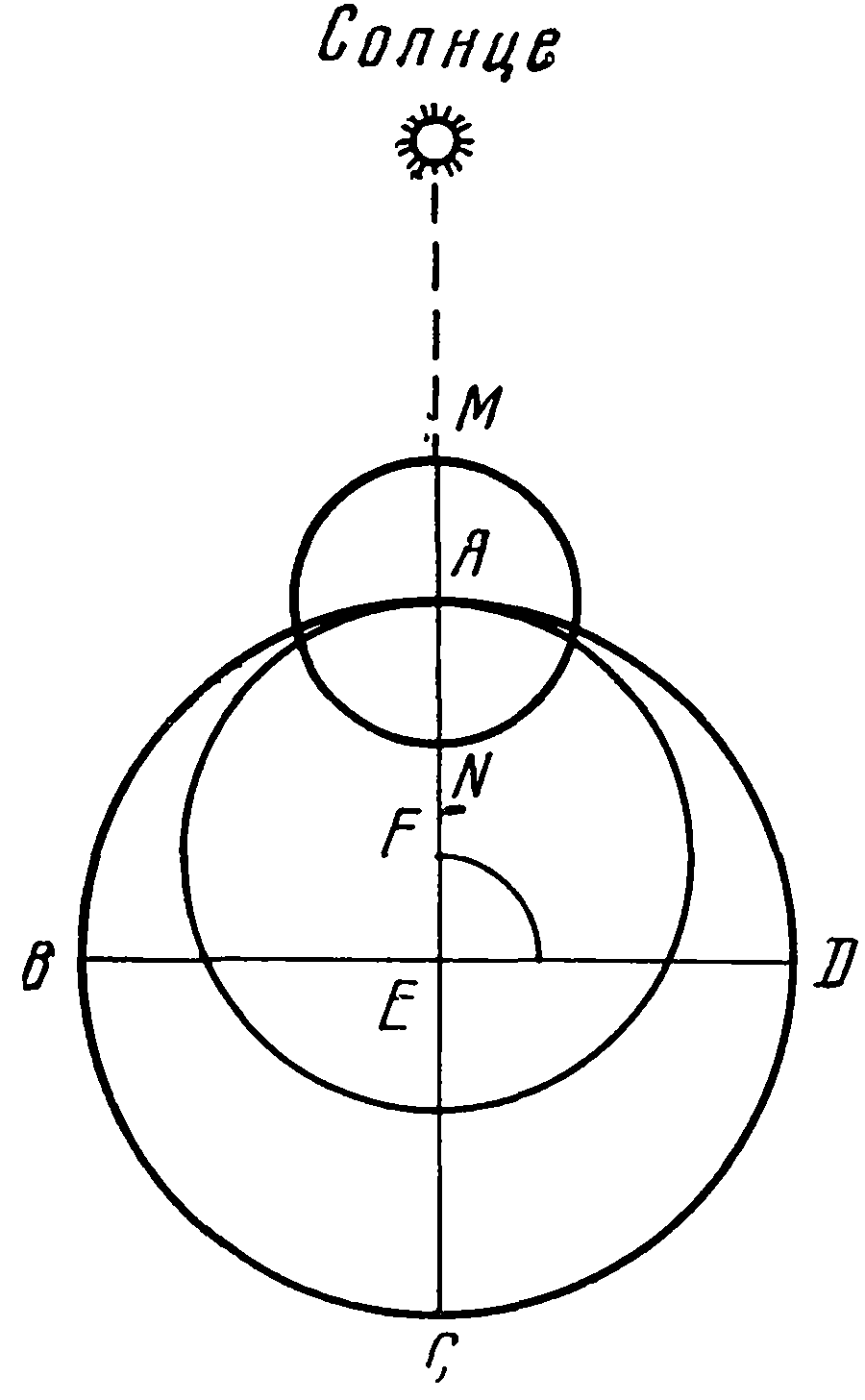
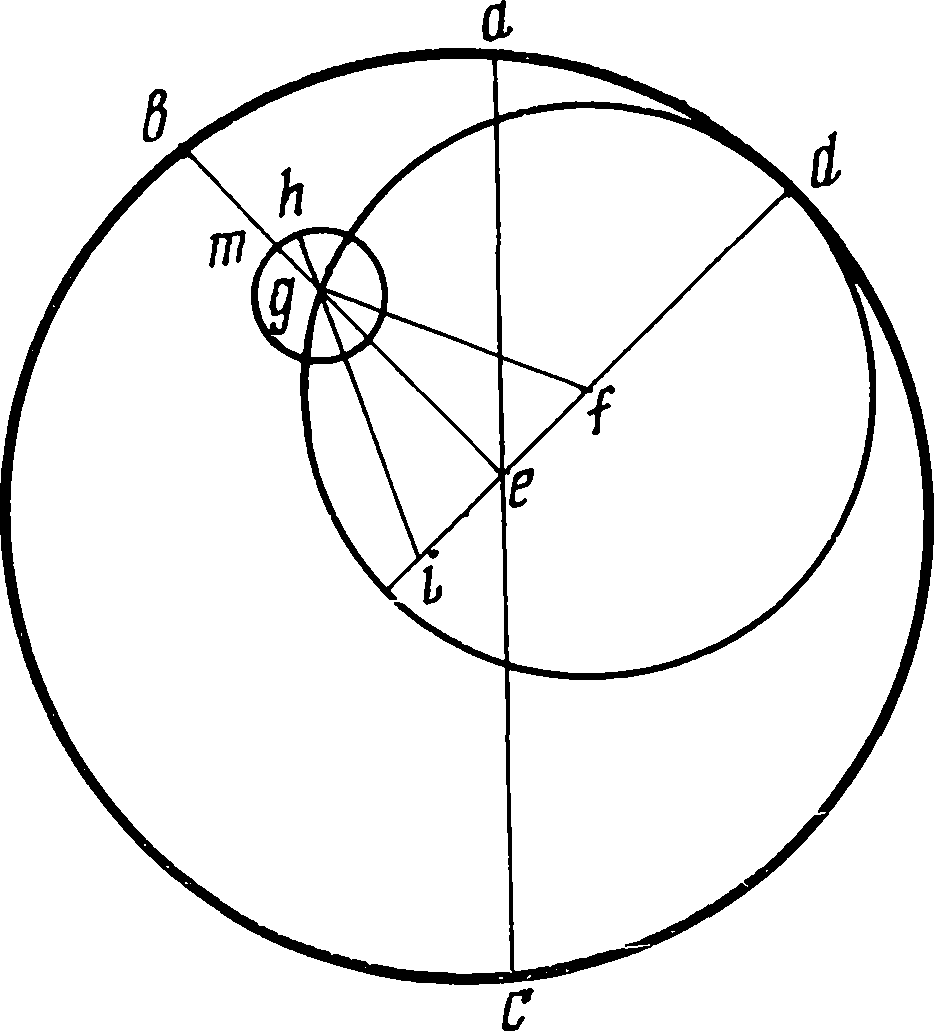
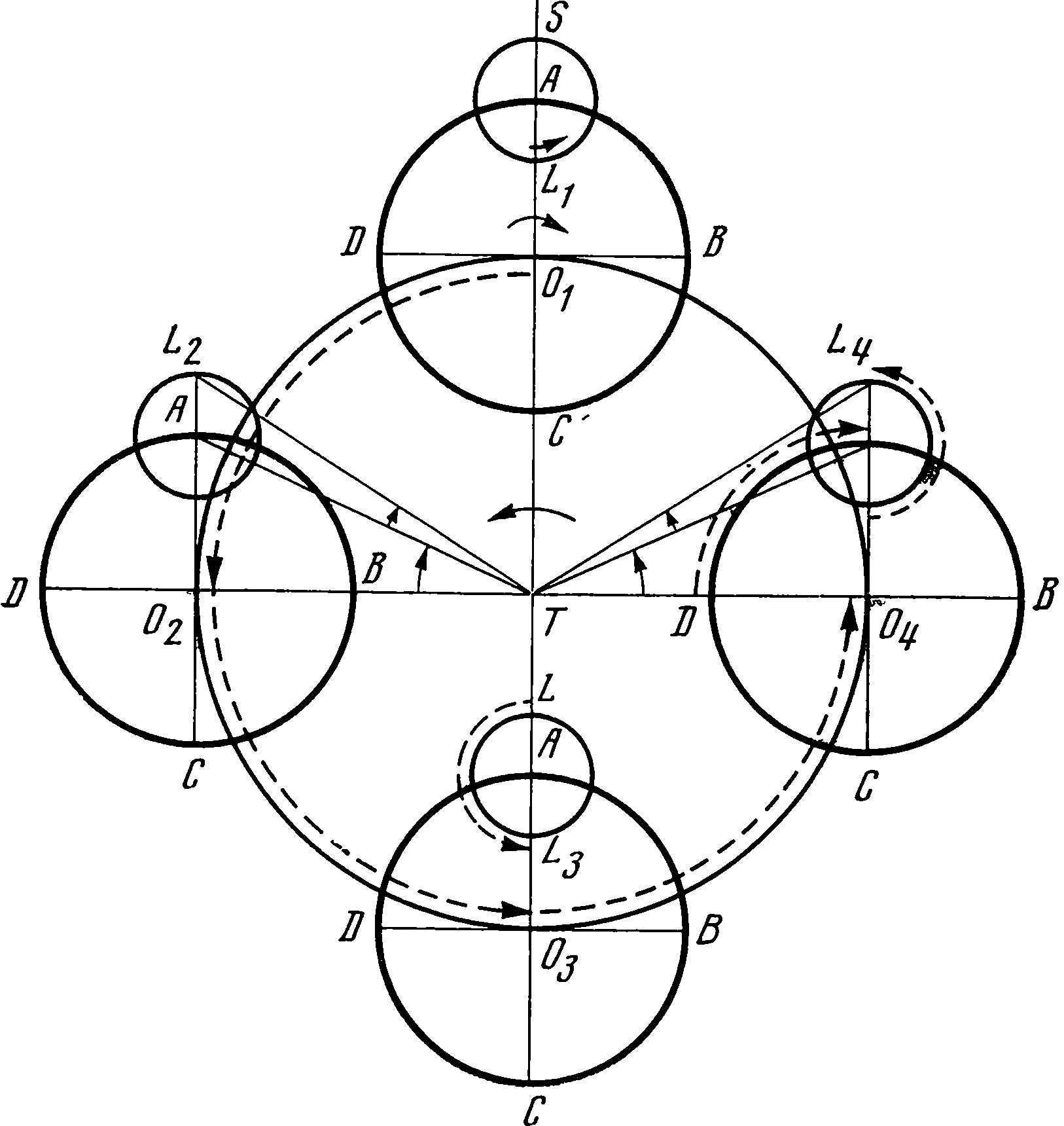
16. Теория движения Луны

Хотя движение Луны и кажется на первый взгляд простым и естественным, его математическое описание связано с преодолением значительных трудностей. Прежде всего давно уже было замечено, что орбита движения Луны не лежит в плоскости эклиптики; в этом причина, что солнечные и лунные затмения не повторяются регулярно в полнолуние и новолуние. Об этом знали еще в Древнем Вавилоне, в Древней Греции — это было установлено Анаксагором в V в. до н. э. По-видимому, вавилоняне уже знали, что точки пересечения лунной орбиты с эклиптикой, так называемые узлы, не остаются неподвижными, а перемещаются с периодом в 19 лет. Дальнейшая разработка теории движения Луны принадлежит Птолемею.

В движении Луны выделено несколько отличающихся один от другого периодов. Одним из них является так называемый синодический месяц — период от одного новолуния до следующего, — он равен 29 дням, 12 часам и 44 минутам; по истечении этого промежутка времени Луна возвращается в первоначальное положение относительно Солнца. Можно ставить вопрос о времени возвращения Луны к начальному положению относительно неподвижных звезд (сидерический месяц) или к началу отсчета долгот — точке весеннего равноденствия (тропический месяц). Так как в прецессионном движении точка весеннего равноденствия движется навстречу светилу, то тропический месяц будет чуть короче сидерического: продолжительность сидерического месяца составляет 27 дней, 7 часов, 43 минуты и 13 секунд, а тропического — на 15 секунд короче.

Еще вавилонские астрономы (III—IV вв. до н. э.) заметили, что скорость движения Луны по орбите не остается постоянной. Это неравенство можно исправить, если предположить, что по окружности (деференту) движется в противоположную сторону с такой же угловой скоростью эпицикл, несущий Луну; когда Луна ближе к Земле, ее скорость больше, а при удалении меньше. Этого же можно было бы добиться и при помощи эксцентрического круга. Тогда в наибольшем удалении (апогее) скорость Луны будет наибольшей, а в перигее наименьшей.

Пусть центр A эпицикла по деференту ABED и Луна по эпициклу двигаются в противоположные стороны, совершая полный оборот относительно прямой AEC, все время проходящей через Солнце, в течение одного синодического месяца (29½ дней). Тогда движение Луны будет казаться наиболее медленным в точке M эпицикла и наиболее быстрым в точке N. Центр F заменяющего эпицикл эксцентрического круга (его нет на чертеже) все время будет находиться на прямой, соединяющей центр E Земли с Солнцем. Это позволяет определить так называемый аномалистический месяц как время, необходимое для последовательного возвращения Луны к апогею или вообще к той же самой скорости. Продолжительность аномалистического месяца равна 27 дням 13 часам и 18½ минуты. Зная положение апогея и точки весеннего равноденствия, можно вычислить среднее движение по долготе λ и среднее движение λ по аномалии; разность между ними λ − λ, равная нулю в сизигиях A и C, будет наибольшей в квадратурах B и D — 5°1′. В действительности оказалось, что ее наибольшая наблюденная величина составляет 7°40′. Это второе неравенство, найденное Птолемеем, получило название эвекции.

Для объяснения этого неравенства Птолемей предположил, что получившийся эксцентрический круг не остается неподвижным, а совершает в течение месяца один оборот по часовой стрелке вокруг Земли по отношению к линии, соединяющей центр Земли с Солнцем. Таким образом, прямая CEA всегда будет биссектрисой угла между линиями, направленными к центрам эксцентрического круга и эпицикла.

Пусть Луна, неподвижная в точке M эпицикла, находится в новолунии и в апогее эксцентрического круга. Если центр этого круга F сделает четверть оборота и окажется на линии ED справа от E, то центр A эпицикла будет на той же линии слева от E, а Луна, находящаяся в точке M эпицикла, совершающего круговое поступательное движение, будет в квадратуре и в перигее эксцентра. Еще через четверть оборота точка F и центр A эпицикла окажутся на прямой EC и ниже точки E, центр эпицикла A будет опять в наибольшем расстоянии, а Луна, находящаяся на линии EC, будет в апогее и в полнолунии. Таким образом описанный механизм приводит к тому, что полнолуния и новолуния совершаются в апогее эксцентра, а квадратуры — в его перигее.

В этом объяснении Коперник видел следующие недостатки. Складывая два вращения с одинаковыми, но противоположными угловыми скоростями, получаем движение по эксцентрическому кругу с изменяющейся скоростью, что, конечно, противоречит основному закону кругового равномерного движения. Во-вторых, в соединениях Луна будет находиться дальше от центра Земли, чем в квадратурах, причем она должна приближаться к Земле приблизительно на половину расстояния, и соответствующее изменение диаметра лунного диска должно быть замечено наблюдателем; в действительности же видимый диаметр Луны все древние астрономы принимали равным всегда половине градуса.

В критическом разборе, которому Коперник подверг лунную теорию Птолемея, есть один момент, имеющий большое значение для дальнейшего развития теоретической астрономии. Во II главе четвертой книги «Вращений» Коперник пишет: «Если признавать равномерным движение центра эпицикла вокруг центра Земли, то следует признать, что движение его по собственной описываемой им орбите, а именно эксцентру, должно быть неравномерным»¹.

Действительно, пусть eac будет линия, проходящая через центр Земли e и Солнце, а efd — линия апсид, где f является центром эксцентрического круга dg.

«Если... взять угол aeb 45 градусов... и отложить aed, равный ему, так, чтобы весь угол bed был прямым, взять центр эпицикла в g и соединить gf, то угол gfd, очевидно, будет больше gef... Поэтому дуги dab и dg, описанные обе в одно и то же время, не будут подобными, ибо dab является четвертью окружности, а дуга dg, которую за то же время описал центр эпицикла, будет более четверти окружности...

Следовательно, движение эпицикла по описываемому им эксцентрическому кругу будет неравномерным. Но если так, то что мы ответим, если нам приведут аксиому: движение небесных тел является равномерным и только по видимости может представляться неравномерным? ...Если же сказать, что он [эпицикл. — Авт.] равномерно движется около центра Земли и этого вполне достаточно для сохранения равномерности, то какой же будет эта равномерность, если она существует в постороннем круге, по которому его движение не совершается в действительности и не существует в собственном эксцентре?

Так же, конечно, мы удивились бы и тому, что и для самой Луны на эпицикле равномерность хотят признать не по отношению к центру Земли (т. е. именно к линии egm...), а по отношению к какой-то другой точке (на чертеже точка i. — Авт.) и что между этой точкой и центром эксцентрического круга находится посередине Земля, а линия igh является как бы указателем равномерности движения Луны по эпициклу, что по самому существу доказывает неравномерность рассматриваемого движения...»²

Точка i у Птолемея называется эквантом: вокруг этой точки совершается равномерное движение находящегося на эпицикле в точке h центра Луны. Коперник, следуя, по-видимому, урокам Брудзевского, хочет уничтожить самую возможность допущения таких точек.

Если мы с современных позиций будем рассматривать точку e как центр эллиптической орбиты планеты, f — фокус, вокруг которого происходит движение с постоянной секторной скоростью, а i — другой фокус, сможем показать, что, если пренебречь членами, содержащими квадрат эксцентриситета, то вращение планеты вокруг второго фокуса i будет представляться равномерным. Конечно, ни Копернику, ни Птолемею не могла прийти в голову мысль о такой возможности, но все же из них обоих Птолемей был ближе к истине, чем Коперник.

Общий механизм движения Луны, по Копернику, может быть представлен таким образом.

Пусть T — Земля, а S — Солнце. Точки O₁, O₂, O₃, O₄ представляют положения Луны на ее орбите в среднем равномерном движении, вращение радиуса TO совершается против часовой стрелки, время полного оборота соответствует синодическому месяцу — промежутку между двумя последовательными новолуниями, иными словами, по истечении синодического месяца Луна возвращается в то же самое положение относительно Солнца. Точка O₁ является центром первого эпицикла. Она перемещается по орбите O₁O₂O₃O₄ в течение синодического месяца, радиус O₁A этого эпицикла вращается в противоположном направлении, т. е. по часовой стрелке, и совершает полный оборот в течение аномалистического месяца — времени между двумя последовательными прохождениями Луны через апогей (на рисунке для простоты мы приняли его равным синодическому, в действительности он меньше).

Нововведением Коперника является второй эпицикл, центр которого движется по окружности первого эпицикла; его последующие положения будут A, B, C, D. Второй эпицикл несет Луну L, он вращается против часовой стрелки и делает полный оборот за половину синодического месяца.

Пусть начальное положение L₁ соответствует новолунию и апогею. Луна в новолунии находится в самой нижней точке второго эпицикла. По истечении четверти синодического месяца радиус TO повернется на 90° и займет положение TO₂, радиус O₁A первого эпицикла повернется примерно на 90° по отношению к радиусу TO₁ и займет положение O₂A Луна сделает вместе со вторым эпициклом пол-оборота и окажется в точке L₂. Если вначале истинное положение Луны совпадало со средним, то теперь для определения истинного положения нужно из средней долготы вычесть угол ATO₂ (так называемое уравнение центра) и угол ATL₂, или эвекцию. Во время движения от O₁ к O₂ оба эти угла, как нетрудно видеть, увеличивались. По истечении второй четверти оборота Луна, сделав еще пол-оборота, по второму эпициклу придет в положение L₃. Уравнение центра и эвекция обратятся в нуль. Сделав еще четверть оборота, Луна перейдет в положение L₄; уравнение центра и эвекция при этом переходе тоже будут возрастать, но только теперь они будут положительными.

В действительности дело обстоит несколько сложнее. Не всегда Луна в новолунии будет находиться в апогее, так что уравнение центра для положений O₁ и O₂ (полнолуние) может быть и не равно нулю, но эвекция в этих случаях должна всегда равняться нулю. Подобным же образом вследствие неравенства синодического и аномалистического месяцев прямые O₁A, O₂A, O₃A, O₄A, не будут параллельными, и по истечении синодического месяца начальное положение не восстановится полностью, но это все лишь несколько осложняющие механизм детали.

В 1957 г. была опубликована работа арабского астронома аш-Шатира, жившего за 200 лет до Коперника, который, объясняя механизм движения Луны, тоже ввел второй эпицикл. Упоминая об этом, О. Нейгебауэр считает, что «знал Коперник о своем предшественнике или нет, в настоящее время установить невозможно»³.

Нам кажется, что ответить на этот вопрос не так уж трудно, достаточно выяснить, каким образом работа аш-Шатира могла стать известной Копернику. Считают, что эта работа, имеющая своей целью исправление лунной теории Птолемея, была переведена на греческий язык, и Коперник во время пребывания в Италии мог с ней познакомиться. Здесь нужно отметить, что Коперник выучил греческий язык около 1500 г., Птолемея он знал в это время лишь по «Эпитоме» Региомонтана, вышедшей в 1496 г., латинский перевод его был у него только с 1515 г. Следовательно, в Италии труд аш-Шатира вряд ли мог его особенно интересовать, во всяком случае до 1523 г., когда он начал работать над четвертой книгой «Вращений». Поэтому гораздо более вероятно, что введение второго эпицикла было им сделано вполне самостоятельно. Кроме того, Коперник всегда указывает свои источники, и достаточно подробно, — стоит вспомнить приведенные им в первой книге античные источники, относящиеся к движению Земли и структуре планетной системы.

Конец четвертой книги «Вращений» посвящен изложению теории затмений и необходимых для этого сведений.

В первую очередь дается изменение широт Луны. Основой для этого был драконический месяц — время, необходимое для того, чтобы Луна, выйдя из восходящего узла орбиты, возвратилась в него же. Продолжительность драконического месяца у Коперника равна 27 дням 12 часам 44 минутам и 18 секундам, что от современного отличается лишь на 0,3 секунды. Разделив 360° на продолжительность драконического месяца, получим среднее дневное движение аргумента, или аномалии широты. Физического значения аргумент широты не имеет; в дальнейшем Коперник отождествлял его с градусами наклонной орбиты Луны, причем нулевая точка, по-видимому, была в северном предельном отклонении Луны от эклиптики. Наибольшее отклонение Луны от эклиптики составляло у Коперника 5°.

После этого определяются параллактические смещения Луны, получающиеся при наблюдении из различных мест земной поверхности и зависящие от географической широты места наблюдения, а затем определяются расстояния Солнца и Луны от Земли, их диаметры и тени в месте прохождения Луны, а также ось тени и, наконец, даются правила для определения возможности затмения для заданных новолуний и полнолуний, а также хода наблюдаемого затмения — его начала, конца, продолжительности и величины затмения.

Хотя общая методика вычисления затмений у Птолемея и Коперника примерно одинакова, в деталях изложения процесса имеются большие различия. В то время как для Коперника и современных ему астрономов существенными были только приведенные выше характеристики, т. е. ход затмения, его продолжительность, величина, для Птолемея это было недостаточным. Вот начало 11-й главы шестой книги «Альмагеста». «Об углах направлений в затмениях». Направления, получающиеся в затемнениях, складываются, во-первых, из направления самого затемнения по отношению к эклиптике и, во-вторых, угла эклиптики с горизонтом. Если бы кто-нибудь захотел проработать все направления, получающиеся в течение затмения в целом, то вследствие необычно большой переменчивости положений в каждой фазе затмения это не дало бы никакой пользы для предсказаний.

Следовательно, вполне достаточно будет произвести это исследование только для затмений, имеющих какое-нибудь предзнаменовательное значение, отмечая лишь в общих чертах дуги, наблюдающиеся на горизонте; это можно сделать непосредственно на глаз, отмечая положения обоих упомянутых направлений.

Что касается затемнения, то мы считаем важным для предсказаний отметить его первую фазу, последнюю и фазу наибольшего затемнения в середине затмения, если оно не является полным, затем первую фазу освещения в конце пребывания в тени и последнюю фазу освещения в конце затмения. Из направлений мы считаем наиболее важными те, которые определяются меридианом и местами восхода и захода точек равноденствий и солнцеворотов на эклиптике; что же касается направлений различных ветров, то их можно обозначить при помощи соответствующих точек горизонта»⁴.

После этого Птолемей указывает на необходимость вычисления получающихся на горизонте расстояний между точками восхода и захода для каждого из двенадцати делений зодиака до пересечения меридиана с горизонтом. В результате получается таблица из 22 строк и четырех столбцов; первый из них показывает затемнение лунного диаметра в средней фазе затмения (в дюймах), второй — углы для солнечных затмений в начале затемнения или в конце освещения, третий — такие же углы для лунных затмений, четвертый (тоже в лунных затмениях) углы в конце затемнения и начале освещения. Двадцать две строки соответствуют числу дюймов от 0 до 21.

Мы видим, что в те времена наблюдателям приходилось производить очень большую работу, от которой Коперник их освободил.

Примечания

1. Николай Коперник. О вращениях..., стр. 227.

2. Николай Коперник. О вращениях..., стр. 227—228.

3. О. Нейгебауэр. Точные науки в древности, стр. 192.

4. Перевод с греческого И.Н. Веселовского.