17. Теория движения планет

В главе VII мы описали историю развития представлений о планетных движениях вплоть до времени Коперника; теперь следует более подробно разобрать положения, внесенные в теорию движения планет самим Коперником.

В современной астрономии видимое движение планет складывается из двух — движения планеты вокруг Солнца по эллиптической орбите, мало отличающейся от окружности, и кажущегося, параллактического, по терминологии Коперника, являющегося следствием движения Земли вокруг Солнца (термином «параллактические смещения» обозначают те изменения видимого положения предмета, которые происходят вследствие движения наблюдателя). В этом движении планеты кажутся описывающими петли около среднего положения, перемещающегося все время против часовой стрелки, — прямым движением, как говорим мы, или в направлении последовательности знаков зодиака, как говорили в эпоху Коперника. Движущиеся таким образом планеты иногда совершают прямые движения, иногда останавливаются, иногда движутся в обратном направлении.

Птолемей в своей теории планетных движений различал два неравенства — первое, которое он называет зодиакальным, связано с различными знаками зодиака, т. е. с соответствующими частями орбиты планеты, второе зависит от положения планеты относительно Солнца. Первое неравенство он объясняет при помощи эксцентрического круга (у Коперника — эксцентра в связи с небольшим эпициклом) второе — при помощи эпицикла (так называемого первого), вращающегося вокруг точки, перемещающейся по эксцентру (этот первый эпицикл у Коперника заменяется параллактическим движением). В «Альмагесте» Птолемей указывает на любопытные соотношения между периодами обращения планеты по эксцентру и эпициклу и солнечным годом. Для верхних планет число оборотов планеты относительно зодиака, сложенное с числом оборотов по эпициклу, дает в сумме число соответствующих тропических лет. Так, для Сатурна за 59 лет происходит 57 оборотов по эпициклу и 2 оборота относительно зодиака, для Юпитера соответствующие числа будут 71, 65 и 6, для Марса — 79, 37 и 42. В настоящее время это весьма просто объясняется как результат сложения угловых скоростей переносного и относительного вращений, дающих в сумме угловую скорость абсолютного движения. Для нижних планет соотношение будет несколько иное — Птолемей отмечает, что для Меркурия и Венеры среднее движение по долготе равно среднему движению Солнца: это показывает, что число оборотов планеты относительно зодиака равно числу соответствующих солнечных лет.

Среднее параллактическое движение планеты (в настоящее время оно называется синодическим), являющееся у Птолемея эквивалентным обращению по эпициклу, представляет разность между средним перемещением Солнца и средним собственным движением планеты. У верхних планет собственное движение меньше движения Солнца, у нижних, наоборот, больше, так что среднее параллактическое движение будет равно разности после вычитания движения Солнца из среднего движения планеты.

Птолемей начал изложение планетных движений с Меркурия и кончил Сатурном, указав, однако, что изложение будет несколько проще, если начать с верхних планет. Коперник так и сделал — он начал рассмотрение планетных движений с Сатурна. Любопытно сравнить значения среднего сидерического движения планет за один египетский год, равный 365 дням, в таблицах Коперника с их современными значениями:

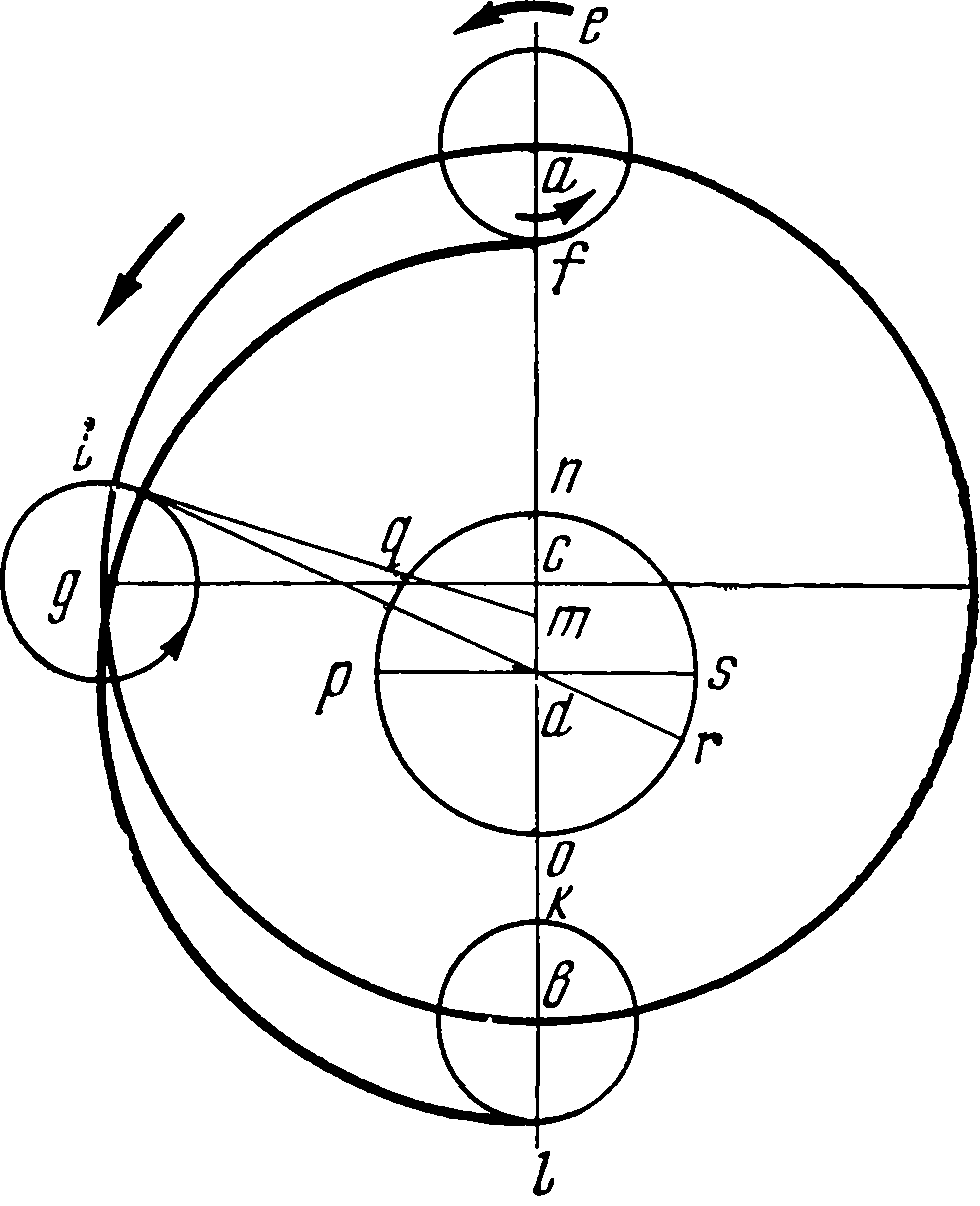
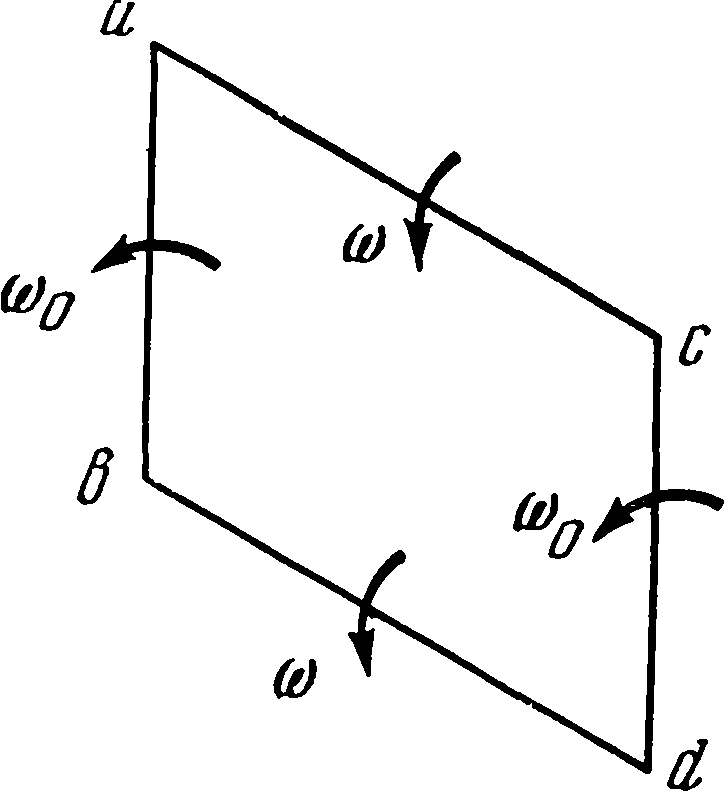
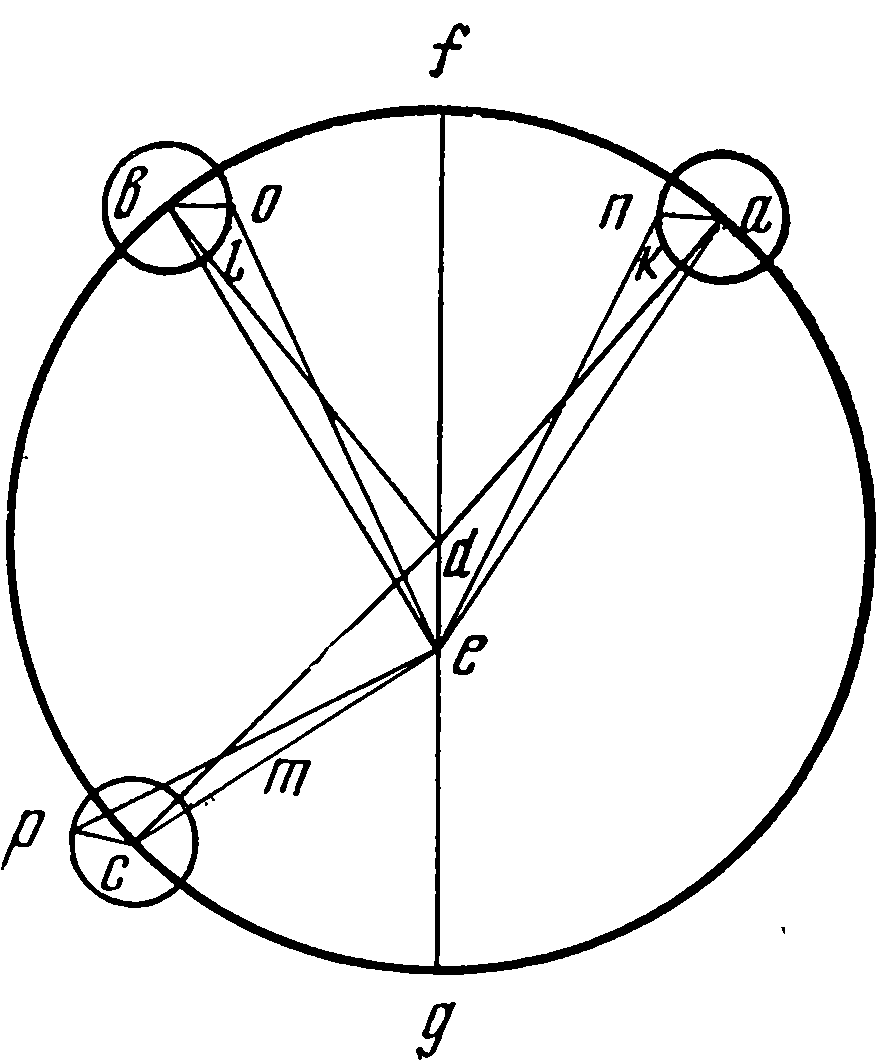
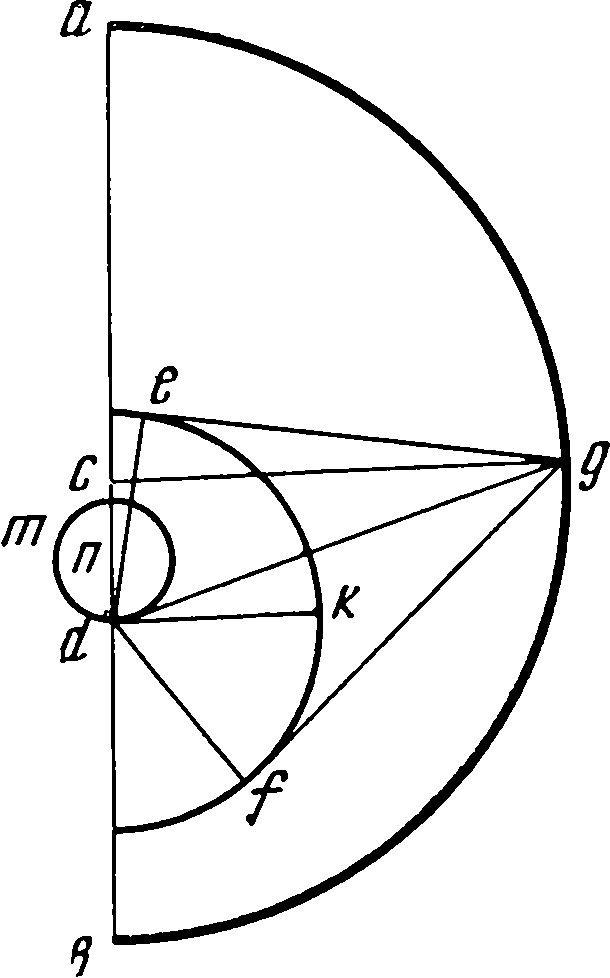
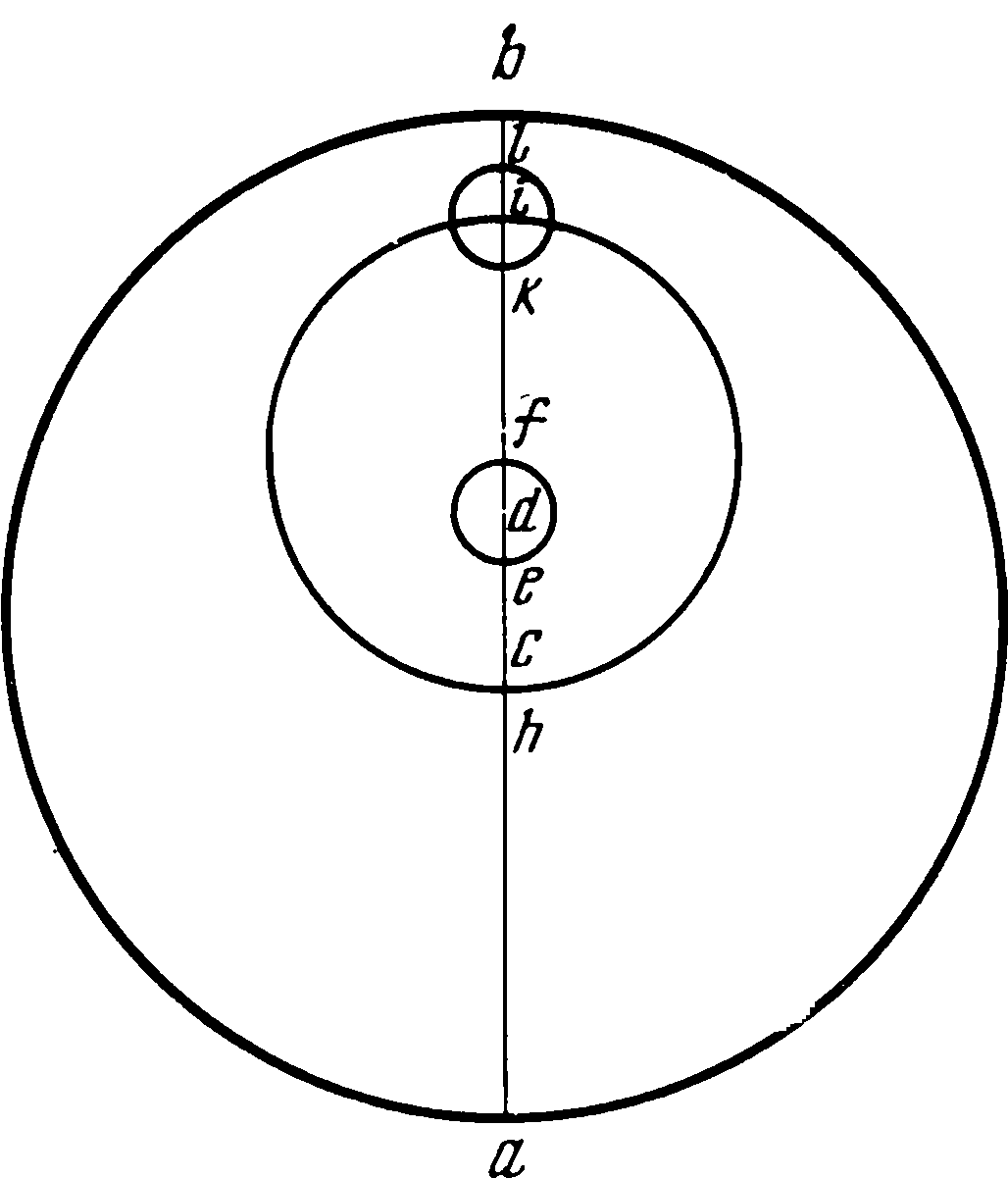
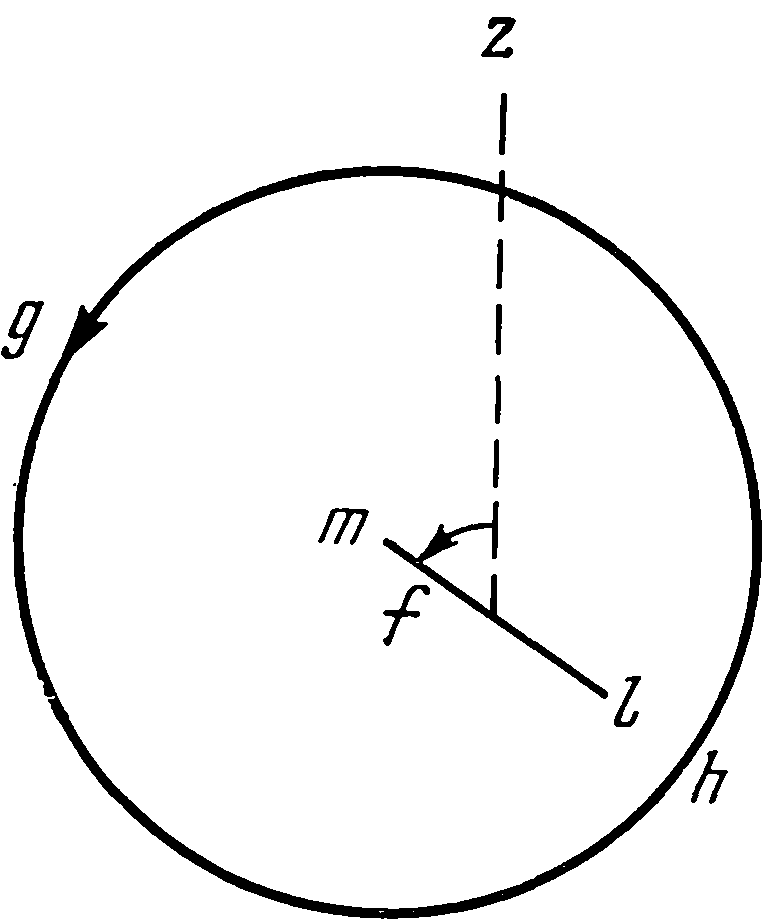
Так как интерес представляет не только полученный результат работы, но и самый процесс ее, то посмотрим, каким образом Коперник определял орбиту планеты и соответствующие характеристики движения. Для этого ему были необходимы три наблюдения положения планеты.

Общая теория движения планет изложена им в IV главе пятой книги «Вращений».

«Итак, пусть ab будет эксцентрический круг, c — его центр и acb— диаметр для среднего положения Солнца, проходящий через верхнюю и нижнюю апсиды планеты; пусть на нем в точке d находится центр орбиты Земли. Взяв центр в верхней апсиде a расстоянием, равным третьей части cd, опишем эпицикл ef, в перигее f которого пусть будет находиться планета. Пусть движение эпицикла по эксцентру ab происходит в направлении последовательности знаков зодиака, движение планеты на верхней дуге эпицикла — также в направлении последовательности, а в остальной части — против последовательности знаков, причем движения их обоих, а именно эпицикла и планеты, имеют одинаковые между собой времена обращения.

Вследствие этого произойдет следующее: если при нахождении эпицикла в верхней апсиде эксцентра планета будет находиться с противоположной стороны в перигее эпицикла, то при прохождении каждой из них своей полуокружности их движения будут совершаться в противоположные стороны. В обеих средних квадратурах эпицикл и планета будут находиться соответственно в серединах своих дуг, и только тогда диаметр эпицикла будет параллелен линии ab, в серединах же соответствующих промежутков он будет перпендикулярен к ab, отклоняясь все время в ту или другую сторону»¹.

«...Опишем теперь из центра d годичную круговую орбиту Земли; пусть она будет no. Продолжим idr и проведем pds параллельно cd; тогда idr будет прямой линией для истинного движения планеты, а gc — для среднего и равномерного. Затем в r будет истинный апогей Земли по отношению к планете, а в s — средний. Следовательно, угол rds или idp будет разностью углов среднего и видимого движений, а именно разностью углов acg и edi»².

В так называемом параллелограмме Аполлония эксцентр ac, имеющий центр в c и вращающийся вокруг точки d, может быть заменен кругом такого же радиуса db, вращающимся вокруг своего центра d и имеющим на конце радиуса эпицикл с центром в b и радиусом ba = cd, угловая скорость вращения которого ω₀ должна быть равна угловой скорости стержня cd. Движение точки a может быть получено одинаково обоими способами. Остается только добавить второй эпицикл с центром a; в первом случае он будет двигаться по эксцентру, во втором — по первому эпициклу. В рассматриваемом у Коперника случае угловая скорость ω₀ = 0.

«Здесь мы выбираем эксцентр с эпициклом потому, что, как оказывается, точка d, оставаясь всегда между Солнцем с центром с, меняет свое положение... Эти предположения вполне соответствуют видимым явлениям... и прежде всего относительно Сатурна, Юпитера и Марса, для которых основным и самым трудным является определение места апогея и расстояния cd ...При этом мы будем пользоваться... сравнением трех древних солнечных противостояний и такого же числа новых. Эти противостояния греки называют акронихическими... Когда планета, прямо противоположная Солнцу, будет находиться на одной прямой со средним положением Солнца, то будет отсутствовать вся неравномерность, которую влечет за собой движение Земли»³.

В соответствии с этим Коперник рассматривает сначала три древних акронихических противостояния, наблюденных Птолемеем во время императора Адриана, и три новых, наблюдавшихся им самим, а именно 5 мая 1514 г. («за один час и пятую часть до полуночи, когда Сатурн оказался на 215 градусах 24 минутах»), затем 14 июля 1520 г. в полдень («на 273 градусах 25 минутах») и наконец 10 октября 1527 г. («в 6 2/5 часа после полуночи, когда Сатурн был виден на 7 минутах градуса от рога Овна»), т. е. β Arietis, долгота которой принималась в качестве начальной точки при отсчете долгот.

«Между первым и вторым наблюдениями прошло 6 египетских лет 70 дней и 33 шестидесятых, в течение которых видимое движение Сатурна составило 68 градусов 1 минуту. От второго до третьего прошло 7 египетских лет 89 дней и 46 шестидесятых, и видимое движение планеты было 86 градусов 42 минуты. Среднее движение в первом промежутке было 75 градусов 39 минут, во втором — 88 градусов 29 минут. При определении верхней апсиды и эксцентриситета сначала следует действовать по предписанию Птолемея, как будто бы планета двигалась только по одному эксцентрическому кругу. Это хотя и не является достаточным, однако при помощи таких приближений мы легче достигнем истинного»⁴.

Это приближение Коперник производит таким образом. Он берет некоторую окружность abc, на которую нанесены места первого, второго и третьего акронихических положений, так что дуги ab и bc равны соответственно 75°39′ и 88°29′. Так как этот круг должен изобразить некоторый эксцентр, то Коперник берет центр d земной орбиты и соединяет его с точками a, b и c; одну соединительную линию он продолжает до пересечения с окружностью. Полученную прямую cde следует испытать, не будет ли она диаметром. Это значит или чтобы сумма дуг ab, bc и неизвестной ae равнялась 180°, или же чтобы длина ce была равна 20 000 — диаметру круга, описанного около треугольников abc или abe; а dc — радиусу этого круга, т. е. 10 000. Коперник выбирает второй путь и из решения треугольников bde и ade находит, что cde = 19 898, а cd = 9299. Это показывает, что d не может быть центром эксцентра; он должен лежать выше d.

Пусть он будет в f. Проводим диаметр fdh и перпендикуляр fk на прямую ce. Решая треугольник fdk, определяем дугу lh — расстояние до перигея h — и убеждаемся, что суммы дуг влево и вправо от hg равны 180°.

Нужно отметить, что угол bde принимается по видимому движению равным 86°42′, в то время как дуга bc среднего движения равна 88°29′.

Теперь второе приближение. Коперник вводит эпициклы.

Первое приближение по установленным местам a, b, c трех наблюденных противостояний позволило определить положение линии апсид fg и расстояние de между центрами. При точках a, b, c строим эпициклы с радиусами, равными ¼ ed, затем, проведя прямые ad, bd, ce, откладываем углы dbo = fdb и dcp = fdc. Линии en, eo и ep, будучи продолжены до окружности эксцентра, дадут исправленные положения противостояний, при помощи которых снова определяем эксцентриситет и положение линии апсид. При введении эпицикла Коперник уменьшает расстояние между центрами, отделяя четверть для радиуса эпицикла, так что в дальнейшем радиус эпицикла будет составлять лишь треть исправленного расстояния между центрами. Потом Коперник еще раз вычисляет все три исходных положения противостояний.

Таким же образом определяются движения Юпитера (три наблюдения: 30 апреля 1520 г., 28 ноября 1526 г. и 1 февраля 1529 г.) и Марса (наблюдения 5 июня 1512 г., 12 декабря 1518 г. и 22 февраля 1523 г.). Приведенные даты показывают, что теория движения верхних планет была закончена Коперником никак не ранее 1530 г.

Много неприятностей доставила Копернику планета Венера. Если бы ее наибольшие расстояния в ту и другую сторону от среднего положения Солнца, а именно утреннее и вечернее, оказались равными друг другу, то можно быть уверенным в том, что посредине двух таких положений Солнца найдется линия апсид эксцентрического круга Венеры. Различие между апсидами можно установить из того, что эти одинаковые отклонения будут меньше вблизи апогея и больше в противоположной точке. Вся теория движений Венеры была достаточно ясно изложена у Птолемея, но, как говорит Коперник, требовалось получить эти результаты из тех же самых наблюдений Птолемея. К сожалению, Коперника подвели имеющиеся в его распоряжении источники, в первую очередь «Эпитома» Региомонтана, а также латинский текст «Альмагеста». Оба источника давали древние наблюдения Теона Смирнского (II н. э. — не смешивать, как это сделал Коперник, с Теоном Александрийским, математиком и отцом знаменитой женщины-математика Гипатии, вторая половина VI в. н. э.). Первое наблюдение Теона было сделано в 16-м году Адриана 21 фармути⁵ (7 марта 132 г.); с ним Птолемей сопоставил свое наблюдение «в 4-й год Антонина 11 тота» (30 июля 140 г.), в латинском же тексте «Альмагеста» неправильно стояло «14-й год Антонина».

Второе наблюдение Теона, по записи в «Эпитоме», было сделано «в 4-м году Адриана 20 атира утром», и его результаты, по расчетам Коперника, сходились с вычисленным положением планеты. Но здесь «небо посмеялось над ним». Дело в том, что через восемь лет Венера возвращается к исходному положению, и в дате можно ошибиться, что с Коперником и случилось; в действительности была правильной имевшаяся в «Альмагесте» дата: «12-й год Адриана 22 атира» (11 октября 127 г.). В паре с этим стояло собственное наблюдение Птолемея в 21-й год Адриана 10 мехира (25 декабря 136 г.).

И еще одна неприятность постигла Коперника (в XXIII главе пятой книги). Сначала в манускрипте было приведено наблюдение Птолемея, произведенное «во втором году Антонина 20 тиби» (16 декабря 138 г.). При вычислениях Коперник убедился, что это наблюдение не может соответствовать действительным движениям Венеры, вычеркнул этот текст и заменил его содержащимся в 4-й главе «Альмагеста» наблюдением Тимохара (12 октября 272 г. до н. э.).

Вычисления с движением планеты Венеры заставили Коперника изменить конструкцию; вместо обычного эпицикла с центром на окружности эксцентра он поместил эпицикл, или, лучше сказать, малый эксцентр, внутри большего. Таким образом, движение Венеры представляется в следующем виде..

Пусть agb будет земная орбита с центром c, а ekf — орбита Венеры с центром d. Расстояние cd между центрами равно 416 частям, каких в cg — радиусе Земли — будет 10 000. Разделим это расстояние пополам в точке m, и на отрезке md, равном 208 частям, построим окружность с центром n, по этой окружности будет перемещаться центр d круговой орбиты Венеры, сама же орбита будет совершать круговой обход таким образом, что когда Земля попадет на диаметр acb, на котором находятся верхняя и нижняя апсиды эксцентра Венеры, то центр планетной орбиты будет находиться в точке m, в средней же дуге, когда Земля будет в точке g, центр орбиты перейдет в точку d на наибольшее расстояние cd. Таким образом, в то время, когда Земля один раз обходит свою орбиту, центр орбиты Венеры совершает двукратное обращение вокруг центра в ту же сторону, что и Земля, т. е. в направлении последовательности знаков зодиака.

При помощи такой гипотезы Птолемей объяснял все особенности движения Венеры. Собственное наблюдение Коперник произвел 12 марта 1529 г. Данная Птолемеем картина движения Венеры остается справедливой и для эпохи Коперника с той лишь разницей, что эксцентриситет Венеры, принимавшийся раньше равным 416, стал приниматься равным 246. Кроме того, места апсид эксцентрического круга оставались у Коперника неизменными — одна на 48 градусах с третью, другая на 228 градусах 20 минутах. Эта его запись (впоследствии зачеркнутая) показывает, что в 1529 г. Коперник еще не знал о движении апсид Венеры. Соответствующий расчет им был произведен после 1532 г.

Еще позднее им разрабатывалась теория движения планеты Меркурия, тем более, что Коперник не имел возможности произвести самостоятельные наблюдения. Поэтому его работа делилась на два этапа: сначала (гл. XXV—XXIX пятой книги) он использует материалы древних наблюдений, а потом, получив наблюдения нюрнбергских астрономов Вальтера и Шонера (гл. XXX—XXXII), присланные к нему значительно позже (во время приезда Ретика), дает другую теорию.

«Из опыта древних наблюдателей известно, что в знаке Весов Меркурий совершает наименьшие отклонения от Солнца, а в прямо противоположном наибольшие, как и подобает. Однако наибольшие отклонения получаются не только в этом месте, но и в некоторых иных по обе его стороны, а именно в Близнецах и Водолее, в частности, во время Антонина, как говорит Птолемей... Вследствие этого древние математики, верившие в неподвижность Земли и в движение Меркурия по большому своему эпициклу на эксцентре, заметив, что один простой эксцентр не может удовлетворительно объяснить эти явления... принуждены были, кроме того, допустить, что этот эксцентр движется по некоторому другому небольшому кругу, неся эпицикл...

Но чтобы и эту последнюю планету избавить от несправедливости хулителей и случайностей и чтобы раскрыть ее равномерность при помощи движения Земли... мы придадим его эксцентру еще один эксцентр вместо эпицикла, который предполагала древность... Кроме того, пусть по этому эксцентру будет двигаться еще некоторый эпицикл <по которому будет перемещаться планета, но не по окружности, а вверх и вниз по, диаметру...>»⁶

Предположим, что у нас имеется орбита Земли с центром c и диаметром acb. На нем мы берем центр d и описываем вокруг него малый круг ef радиусом, равным третьей части cd, так, чтобы в f получалось наибольшее расстояние от центра c земной орбиты, а в e наименьшее. Около центра f опишем орбиту Меркурия hi; затем прибавим эпицикл, по которому будет двигаться планета, взяв центр его в верхней апсиде i. Диаметр kl этого эпицикла равен 380 частям, если радиус орбиты Земли принят за 10 000; центр i этого эпицикла двигается по окружности ih эксцентра, делая полный оборот за время собственного движения Меркурия вокруг Солнца, т. е. приблизительно за 88 дней: радиус fi этого эксцентра равняется 3947 частям. Центр f перемещается по окружности с радиусом fd, равным 212 частям, и совершает два оборота в течение года. Движения происходят таким образом, что, когда точки l, i, k, f, d лежат на одной прямой, планета оказывается или в l, или в k; если она находится в k, то центр f лежит между k и d (это бывает при нахождении Земли в верхней или нижней апсиде Меркурия), если же планета будет в i, то, наоборот, центр d будет лежать между f и i.

Пусть, кроме того, планета совершает вокруг центра i колебательное движение по прямой между k и l. Как мы уже упоминали, Нейгебауэр это называет «способом ат-Туси». Недоумение Нейгебауэра относительно «приоритета ат-Туси» вполне разрешается также уже упоминавшейся припиской Коперника на полях манускрипта о том, что перемещение планеты по эпициклу будет совершаться «не по окружности, а вверх и вниз по диаметру, что также может быть получено при помощи сложения равномерных круговых движений. И это не удивительно, так как Прокл в комментарии к «Началам» Евклида признает, что прямую линию можно описать несколькими движениями»⁷. Ссылка на Прокла (411—485) полностью реабилитирует Коперника в заимствовании у ат-Туси. Более вероятно, что последний, разрабатывавший вопросы о пятом постулате Евклида, должен был знать и комментарий Прокла к первой книге Евклида.

Двадцать девятой главой пятой книги «Вращений» первоначально заканчивалось сочинение Коперника; содержащиеся в XXXIII и XXXIV главах таблицы были вначале лишь эпилогом к пятой книге. Главы XXX—XXXII, относящиеся ко второму этапу работы Коперника над теорией движения Меркурия, написаны в отдельной тетради, имеющей характер вставки. Так как в этой тетради содержатся также главы XXXV и XXXVI, первая из которых представляет перевод греческого текста Птолемея, привезенного Ретиком в качестве подарка Копернику, то их составление можно отнести к 1539—1540 гг.

На втором этапе работы над теорией движения Меркурия Коперник опирался на наблюдения, произведенные в Нюрнберге учеником Региомонтана Бернардом Вальтером 9 сентября 1491 г., а также Иоганном Шонером 9 января и 18 марта 1504 г. Иоганн Шонер нюрнбергский математик и астроном, преподававший с 1526 по 1547 г. математику в Нюрнбергской гимназии, был учителем Ретика. Известный коперниковед Биркенмайер считает, что наблюдения 1504 г. тоже принадлежат Вальтеру, умершему в 1504 г., и отнесение их к Шонеру неправильно⁸.

Вторая схема движения Меркурия состоит в следующем. Планета движется по эксцентру gh с центром m, совершая оборот в один год; центр m колеблется по прямой mfl тоже с годичным периодом, но удвоенная амплитуда ml колебания равна сумме диаметров эпицикла kl и малого круга fd первой схемы (424 + 380 примерно равно 800), т. е. приблизительно удвоенному диаметру окружности fd. Сама же эта прямая вращается вокруг центра f с угловой скоростью, равной разности угловых скоростей Меркурия и Земли в их обращениях вокруг Солнца.

Интересно определить, какова точность на практике таблиц Коперника. Резюме исследований по этому поводу А.Ф. Мебиуса дано Е.Ф. Аппельтом⁹ для наиболее интересной планеты — Марса. Если орбита планеты имеет значительный эксцентриситет и учитываются только его первые степени, то вычисленные гелиоцентрические долготы могут отличаться от истинных на 37 минут (если исходить из истинного положения Солнца). Если же, как делает Коперник, исходить из центра земной орбиты, то ошибки в определении гелиоцентрической долготы Марса могут достигнуть 2 градусов. Эта ошибка еще увеличивается вследствие того, что орбита Земли является тоже эллиптической; таким образом, полученные при помощи таблиц Коперника положения Марса могут отличаться от истинных на целых 3 градуса.

Примечания

1. Николай Коперник. О вращениях..., стр. 309—310.

2. Там же, стр. 311.

3. Николай Коперник. О вращениях..., стр. 311.

4. Там же, стр. 316.

5. «Фармути» и встречающиеся далее в тексте «тота», «атира» и т. д. — названия месяцев египетского календаря.

6. Николай Коперник. О вращениях..., стр. 352—353. Слова в угловых скобках написаны Коперником на полях манускрипта.

7. Николай Коперник. О вращениях..., стр. 353.

8. В 1504 г. Шонер в Нюрнберге еще не жил.

9. См. E.F. Appelt. Die Reformation der Sternkunde. Jena, 1852, S. 158, 261.