В.А. Бронштэн

КЛАВДИЙ ПТОЛЕМЕЙ

* Предисловие * Глава 1 — Место и время действия * Глава 2 — Астрономия в Вавилоне и Греции до Гиппарха * Глава 3 — Астрономические исследования Гиппарха * Глава 4 — Краткое содержание «Альмагеста» * Глава 5 — Мировоззрение Птолемея * Глава 6 — Небесная сфера: расчеты и измерения * Глава 7 — Теория движения Солнца * Глава 8 — Теория движения Луны * Глава 9 — Звездный каталог * Глава 10 — Теория движения планет * Глава 11 — «Преступление Клавдия Птолемея» * Глава 12 — Работы Птолемея в области географии * Глава 13 — Работы Птолемея в области оптики * Глава 14 — Математика и музыка * Глава 15 — Птолемей и астрология * Глава 16 — Судьба «Альмагеста» * Глава 17 — От эпициклов Птолемея к законам Кеплера * Птолемеи и Коперник (послесловие редактора) * Литература *

Глава 3

Астрономические исследования Гиппарха

В отличие от всех античных ученых, с чьими трудами мы познакомились в гл. 2, Гиппарх был, во-первых, «чистый» астроном — он не занимался одновременно вопросами математики, как Архимед или Аполлоний, или философией, как Аристотель, не ограничивал свои исследования узкими прикладными проблемами, как Метон, Эвктемон и Каллипп, не был только лишь наблюдателем, как Аристилл и Тимохарис. В то же время оп не стремился оторваться от привычных представлений о строении мира подобно Гераклиду Понтийскому и Аристарху Самосскому. Гиппарх был весьма разносторонним астрономом. Оп хорошо понимал основные задачи, стоявшие перед астрономией в его эпоху, и приложил все усилия, чтобы их решить или хотя бы способствовать их решению.

Гиппарх работал в не очень благоприятных условиях. У него не было на Родосе коллег и сотрудников, по крайней мере мы ничего о них не знаем. Если Метон и Эвктемон, Аристилл и Тимохарис, Архимед и Эратосфен могли так или иначе общаться друг с другом, то Гиппарх, казалось бы, был лишен такой возможности. Возможно, у него были ученики и ближайшие помощники, но они не оставили следов в истории науки.

Работая на Родосе, Гиппарх не имел в своем распоряжении и Александрийской библиотеки. Правда, научная библиотека на Родосе была, иначе откуда бы он узнал о работах Каллиппа, Тимохариса, Аристилла, Аристарха, Эратосфена и других ученых, чьи наблюдения он использовал. Более того, достоверно известно, что Гиппарх поддерживал связи с александрийскими астрономами того времени и знал об их наблюдениях. Так, он сравнивал наблюдения с экваториальным кольцом момента весеннего равноденствия — 145 марта 24 в Родосе и в Александрии и нашел между ними расхождение на несколько часов [17. С. 134].

В то время не было почты в нашем понимании этого слова. Но переписка была. Например, в 1906 г. было обнаружено письмо Архимеда к Эратосфену, в котором Архимед развивает метод нестрогого доказательства, имеющего целью получение результата, который затем следует доказать уже совершенно строго [87]. Вполне возможно, что для обмена письмами с александрийцами Гиппарх использовал купцов, чьи корабли регулярно поддерживали связь между Родосом и Александрией.

Перейдем к обзору научных исследований Гиппарха в области астрономии. При этом мы не будем вдаваться в подробности, поскольку почти все работы Гиппарха были так или иначе использованы и продолжены Птолемеем, и мы к ним вернемся, когда будем описывать труды последнего.

Работы Гиппарха можно сгруппировать по следующим шести проблемам. Это — проблемы календаря, исследования прецессии, составление звездного каталога, движение Солнца, движение Луны, движение планет.

Проблема календаря имеет давнюю историю, и о некоторых аспектах этой проблемы мы уже говорили. Гиппарх посвятил этой проблеме два своих сочинения, упоминаемых Птолемеем и, увы, не дошедших до нас: «О длительности года» и «Об интеркаляционных месяцах и днях» (так назывались «вставные» месяцы и дни в древних календарях, например тринадцатый месяц, о котором мы уже упоминали) [17. С. 139].

Гиппарх в своих работах использовал каллипповы циклы для нумерации годов. Эти циклы начинались с летнего солнцестояния. Так, первый год первого цикла начался в летнее солнцестояние —329 г. Но для обозначения дат Гиппарх использовал египетский календарь с «плавающим» началом. Во времена Гиппарха египетский год начинался в конце сентября. Это расхождение начал годов каллиппова цикла и египетского календаря могло привести к расхождению на 1 г. в датировке наблюдений, выполненных между началами года по обеим календарным системам. Такие случаи были и не раз обсуждались историками науки. В случае солнечного или лунного затмения такое расхождение разрешается однозначно с помощью «Канонов затмений» или расчетов на ЭВМ, но другие наблюдения могут пострадать от этой неоднозначности.

Одной из задач Гиппарха было определение точной длительности тропического года, т. е. промежутка времени от одного весеннего равноденствия до следующего. Этот период — период смены времен года —играет основную роль и в годовых ритмах живой природы, и в трудовой деятельности человека, в первую очередь в земледелии и скотоводстве. Из-за явления прецессии тропический год на 20 мин короче сидерического года (периода обращения Земли вокруг Солнца или, с точки зрения Гиппарха и Птолемея, Солнца вокруг Земли).

В своем сочинении «О длительности года» Гиппарх доказывает, что тропический год короче 36574 сут на очень маленькую величину, которую можно определить лишь за достаточно длительный промежуток времени. Эта разница будет проявляться в систематическом смещении дат равноденствий и солнцестояний относительно дат каллиппова цикла (в котором, как мы помним, средняя длина года составляет 36574 сут). В этом сочинении Гиппарх утверждает, что за время, прошедшее от наблюдения солнцестояния Аристархом в —279 г. до его собственного наблюдения в — 134 г., т. е. за 145 лет, разница составила половину суток, иначе говоря, одни сутки накапливались за 290 лет. В другом сочинении («Об интеркаляционных месяцах и днях») Гиппарх определяет, что разность в одни сутки накапливается за 300 лет [17. С. 139]. В действительности в эпоху Гиппарха сутки накапливались за 132 года (сейчас — за 128 лет). Таким образом, в определении длительности тропического года Гиппарх допускал ошибку в 6 мин. Его тропический год был короче юлианского (36574 сут) почти на столько же, на сколько он был длительнее действительного значения.

Открытие явления прецессии (предварения равноденствий) является важной научной заслугой Гиппарха. Он пришел к этой идее именно на основании различия длительности сидерического и тропического годов. Это различие было известно еще предшественникам Гиппарха, которые, однако, не могли его объяснить. Гиппарх дал этому явлению правильное объяснение, как видно из заглавия его труда: «О смещении точек солнцестояний и равноденствий» [17. С. 132—133, 327]. В этом он был ближе к истине, чем Птолемей, который считал, что «сфера неподвижных звезд» поворачивается относительно равноденственных точек в прямом направлении, т. е. в сторону возрастающих долгот [17. С. 321].

Гиппарх определил, что прецессия происходит вдоль эклиптики, т. е. изменяются (возрастают) только долготы звезд, а широты остаются неизменными [17. С. 329].

Величину постоянной прецессии Гиппарх мог определить из сравнения положений Спики и других звезд относительно точки осеннего равноденствия в эпоху Тимохариса и в, свое время. Вот что пишет об этом Птолемей в «Альмагесте»: «В своем сочинении „О смещении точек солнцестояний и равноденствий" Гиппарх при точном сравнении наблюдений лунных затмений, выполненных в его время, с теми, которые раньше наблюдал Тимохарис, пришел к выводу, что в его время Спика опережала осеннее равноденствие на 6°, а во времена Тимохариса — на 8°» [17. С. 327]. Таким образом, за 169 лет прецессия по долготе составила 2°, откуда следует, что постоянная прецессии равна 43" в год.

В цитатах из Гиппарха, приводимых Птолемеем, это значение не фигурирует. Птолемей приводит следующее место из сочинения Гиппарха «О длительности года»: «Если по этой причине солнцестояния и равноденствия за один год отступают по меньшей мере на 1/100 градуса, то они должны отступать по крайней мере на 3° за 300 лет» [17. С. 328]. Таким образом, Гиппарх здесь приводит значение постоянной прецессии 36" в год в качестве нижнего предела этой величины. Это вполне согласуется с приведенным выше значением 43", вытекающим из наблюдений Спики.

Ниже мы узнаем, что Птолемей, не придав значения оговоркам Гиппарха (набранным в разрядку), принял в качестве постоянной прецессии именно 36" в год вместо правильного значения 50" или хотя бы значения, полученного Гиппархом, 43" в год. К каким последствиям это привело, мы скоро узнаем.

Величайшей заслугой Гиппарха перед астрономической наукой явилось составление звездного каталога — первого звездного каталога, дошедшего до нас. Этот каталог приводится Птолемеем в «Альмагесте». В нем 1022 звезды [17. С. 341—399]. Птолемей пишет, что он привел в этом каталоге положения звезд по наблюдениям Гиппарха и по своим собственным наблюдениям. Историков науки давно уже беспокоит вопрос, какое количество звезд было в каталоге Гиппарха, а сколько добавил к ним Птолемей. По мнению одних специалистов (Ф. Болл, И.Л. Дрейер), Гиппарх наблюдал положения 850 звезд [98], остальные 175 добавлены Птолемеем. С другой стороны, недавнее исследование американского ученого Д. Роулинса [125] привело его автора к твердому заключению, что все звезды каталога наблюдались именно Гиппархом на широте Родоса (36°), поскольку в нем нет ни одной звезды, которая могла быть видна в более южной Александрии (31°), но не наблюдалась на Родосе. К этому вопросу мы еще вернемся. Важно лишь то, что большая часть звезд каталога наблюдалась именно Гиппархом.

Как бы прелюдией к работе над звездным каталогом явилось единственное сочинение Гиппарха, дошедшее до нас, — «Комментарий к Арату» [114]. Напомним, что Арат — греческий поэт, живший в III в. до п. э. при дворе македонского царя Антигона Гоната и изложивший в одной из своих поэм расположение на небе созвездий и звезд. В «Комментарии к Арату» Гиппарх рассматривает положения на небе около 350 звезд. Но тогда Гиппарх еще не применял последовательно эклиптические координаты — долготу и широту. Из 470 приводимых им координат звезд 64 — склонения, 67 —прямые восхождения (экваториальные координаты) , а остальные — дуги эклиптики от точки весеннего равноденствия до пересечения с кругом склонения звезд, а не с кругом широты, как при счете долгот. Там же приведены моменты восходов, заходов и кульминаций звезд. Это сочинение написано Гиппархом не только до составления звездного каталога, но и до его работ по прецессии [75, 117].

Вот как оценил труд Гиппарха известный римский историк и естествоиспытатель Плиний Старший (23—79 гг. н. э.): «Этот Гиппарх, который не может не заслужить достаточной похвалы, так как он более чем кто-либо доказал родство человека со звездами и то, что паши души являются частью неба, исследовал новую звезду, появившуюся в его время; ее движение в то время, когда она блистала, навело его на мысль, не могут ли часто изменяться и перемещаться те (светила), которые мы считаем неподвижными; поэтому он решился па дело, смелое даже для бога — перечислить для потомства звезды и пересчитать светила, придумав приборы, которыми определил места и яркость отдельных звезд, чтобы можно было легко разобрать: исчезают ли они, появляются ли вновь, не движутся ли или увеличиваются и уменьшаются (в яркости), оставив потомкам небо в наследство, если нашелся кто-нибудь, кто принял бы это наследство» [122].

Эти слова заимствованы из капитального труда Плиния «Естественная история». Новая звезда, о которой идет речь, вспыхнула в созвездии Скорпиона в —133 г. (согласно китайским хроникам, обработанным французским ученым Э. Био). Выражение «ее движение» некоторые ученые переводят как «изменение» (блеска). Однако нет ничего невозможного в том, что очевидцам казалось, будто новая звезда перемещается относительно других.

Характеристика значения труда Гиппарха, данная Плинием, жившим спустя 200 лет после него, вполне может быть подтверждена и в наши дни.

Большое значение имело построение Гиппархом теории движения Солнца. Обнаруженное еще Эвктемоном и уточненное Каллиппом, а затем самим Гиппархом неравенство длительностей сезонов позволило Гиппарху получить все данные об орбите Солнца вокруг Земли. Гиппарх считал, что Солнце движется по эксцентру, и принял так называемую гипотезу простого эксцентриситета. Она состоит в следующем [54].

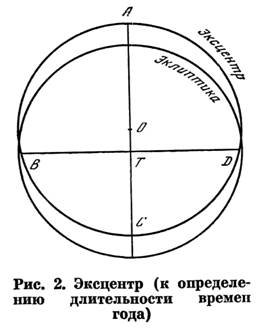
Представим себе (рис. 2) круг расположенный эксцентрично по отношению к эклиптике, но имеющий с ней одинаковый радиус. Отношение расстояния ОТ между центрами обоих кругов к радиусу назовем эксцентриситетом.

Точка С на эксцентре, ближайшая к Земле (т.е. к центру эклиптики), называется перигеем, самая далекая А — апогеем. Предполагается, что Солнце движется по эксцентру равномерно.

Гиппарх сначала определил среднее суточное движение Солнца. Для этого он поделил 360° на определенную им ранее длину тропического года — 365,24667 сут. Получилась величина μ=3548,287", которая лишь на 0,042" меньше действительной [54].

Проведем через точку Т (Землю) две взаимно перпендикулярные прямые, которые отсекут на эксцентре четыре неравные дуги. Одна из этих прямых должна пройти через точки равноденствий, другая — через точки солнцестояний. Требуется так подобрать эксцентриситет и долготу перигея, чтобы дуги АВ, ВС, CD и DA были бы пропорциональны длительностям соответствующих сезонов.

Гиппарх решил эту геометрическую задачу и получил [17. С. 155, 157, 166] эксцентриситет ε = ¹/₂₄, долготу перигея Солнца П=65°30' и наибольшее уравнение центра Солнца x_max = arcsin ε =2°23'. Уравнением центра Гиппарх называл отклонение положения центра Солнца от среднего Солнца, движущегося по эклиптике со средним суточным движением μ (равномерно) и выходящим из точки весеннего равноденствия одновременно с центром истинного Солнца. Это отклонение истинного Солнца от среднего получило название первого неравенства.

Обратим здесь внимание читателя на то, что термины «уравнение» и «неравенство» имели в те времена иные значения, чем теперь. Ими обозначались не математические выражения типа ах=b или а<b, а отклонения от равномерного движения, выраженные, как правило, в угловых единицах. В астрономии до сих пор применяют такие термины, как «уравнение центра», «уравнение времени», хотя это не уравнения, а величины, представляющие отклонения от равномерного движения.

Значения, полученные Гиппархом, мало отличались от точных значений, которые получились бы по его теории. Известный советский астроном и историк науки Н.И. Идельсон попробовал применить теорию Гиппарха к современным положениям Солнца [54], сделав соответствующие расчеты для 1942 г. (Эта работа выполнялась в 1943 г., накануне 400-летия со дня выхода в свет труда Коперника «О вращениях небесных орбит».) Вот что получилось:

Буквой L обозначена средняя долгота Солнца для момента 1942 марта 21, 5 ч 50 мин. Как видим, согласие теории Гиппарха, описывавшей видимое движение Солнца, с современной теорией более, чем хорошее. Как отмечает Н.И. Идельсон, если бы мы построили таблицу долгот Солнца по теории Гиппарха, то в течение нескольких ближайших десятилетий погрешности не превысили бы 1—2 мин дуги¹.

Птолемей использовал теорию Гиппарха для Солнца, по усложнил ее для планет, о чем мы расскажем дальше. Однако, применяя теорию Гиппарха к Солнцу, Птолемей допустил ошибку, приняв без всяких к тому оснований, что долгота перигея Солнца постоянна. Между тем мы видели выше, что значение П в 1942 г. отличается от П в эпоху Гиппарха на 36°30'. Поделив эту величину на 21 (число протекших столетий), мы найдем, что долгота перигея Солнца увеличивается на 1°43' за столетие. Этот факт был обнаружен уже в IX в. Сабитом ибн Коррой и аль-Баттани [54].

От работ Гиппарха берет начало и теория движения Луны. Луна среди других перемещающихся светил занимает особое положение: она действительно обращается вокруг Земли. Когда Коперник через 17 веков после Гиппарха перенес центр планетной системы с Земли в Солнце, теория движения Солнца Гиппарха—Птолемея была им легко приспособлена для описания движения Земли вокруг Солнца. Ведь Коперник сохранил равномерные круговые движения, а с ними он был вынужден сохранить и эксцентр, только по нему двигалась Земля, а не Солнце. Вместо солнечного перигея был введен перигелий — ближайшая к Солнцу точка орбиты Земли, вместо апогея — афелий².

Для Луны эта процедура была не нужна. Но движение Лупы было много сложнее, чем видимое движение Солнца. Прежде всего ее путь был наклонен к эклиптике на угол в 5°, что определил также Гиппарх с ошибкой всего в 8'. Поэтому у Лупы изменялась не только долгота, по и широта.

Далее выяснилось, что период возвращения Луны к перигею своей орбиты, так называемый аномалистический месяц, не равен звездному (сидерическому) месяцу, т. е. периоду обращения Луны вокруг Земли относительно звезд. Аномалистический месяц (названный так потому, что угол отстояния Луны от апогея назывался у древних астрономов аномалией) был длиннее сидерического. Период же возвращения Луны по широте, т. е. период между двумя пересечениями ею эклиптики с юга на север (или с севера на юг), был короче сидерического месяца[54].

Используя наблюдения вавилонских астрономов (которых Птолемеи называет «халдеями»)³, Гиппарх нашел довольно точные соотношения между всеми периодами Луны (месяцами). Как свидетельствует Птолемей, Гиппарх показал, пользуясь наблюдениями «халдеев» и своими собственными, что «наименьшее число дней, после которого затмения повторяются через одинаковое число месяцев и при одинаковых движениях, равно 126 007 дням и одному равноденственному часу; он находит в нем 4267 полных синодических месяцев, 4573 возвращения по аномалии, 4612 возвращений по долготе без 7¹/₂°, которых недостает Солнцу, чтобы закончить 345 оборотов по отношению к неподвижным звездам»; он же нашел далее, что за «5458 месяцев происходит 5923 возвращения Луны по широте» [54. С. 206-209].

Из этих соотношений, которые Н.И. Идельсон справедливо называет циклами Гиппарха, можно получить длительности всех месяцев с удивительной точностью. Приведем их здесь.

Месяц (период) Гиппарх Современные данные

Синодический 29,530592 29,530588

Сидерический (возвращение но долготе) 27,321679 27,321661

Аномалистический 27,554568 27,554551

Драконический (возвращение по широте) 27,212218 27,212220

Термин «драконический месяц», введенный в средние века, отражает легенду о том, что Солнце и Луна во время затмений пожирались драконом. Даже современные обозначения узлов (точек пересечения плоскостей орбиты с плоскостью эклиптики) и напоминают соответственно голову и хвост дракона.

Поражает точность, с которой Гиппарх сумел определить длительность всех четырех месяцев. Расхождения с современными значениями для синодического и драконического месяцев не превосходят 0,35 с и лишь для сидерического и аномалистического месяцев достигают 1,5 с. Такой точности ему удалось достигнуть, использовав наблюдения затмений и положений Лупы за достаточно большой срок — 345 лет. Это значит, что в распоряжении Гиппарха были наблюдения вавилонских астрономов («халдеев») по крайней мере с V в. до н. э., а возможно, и более ранние. Лунные затмения, упоминаемые в «Альмагесте», ведут счет с VIII в. до н. э. Несомненно, что и они были использованы Гиппархом.

Однако это еще не все, что дали исследования Гиппарха для развития лунной теории. Полученные им соотношения для длин месяцев позволяли найти три основных параметра, сыгравшие в дальнейшем важнейшую роль при построении динамической теории движения Лупы на основании законов ньютоновой механики [54]

Пусть n₁ n₂, n' — средние суточные движения перигея и узла лунной орбиты и Солнца соответственно. Разделим их на n — среднее суточное движение Луны по долготе.

Получим, используя данные Гиппарха,

Найденные Гиппархом значения Т₁ и Т₂ лишь на 0,4 и 3,4 сут соответственно отличались от современных. Ясно, что линия, соединяющая перигей и апогей (ось апсид), поворачивается в ту же сторону, что и Луна, поэтому Луне приходится как бы догонять свой перигей и аномалистический месяц оказывается длиннее сидерического. Линия узлов, напротив, движется навстречу Луне, поэтому драконический месяц короче сидерического. Объяснение этих движений дала только небесная механика, основанная на законе всемирного тяготения Ньютона. Но величайшей заслугой античной науки, и в первую очередь Гиппарха, является обнаружение этих движений, а с ними — всей сложности движения Луны вокруг Земли. Эта сложность вступала в разительное противоречие с идеями Аристотеля о наиболее совершенных — круговых и равномерных — движениях небесных тел вокруг Земли.

Отмечая значение обнаружения всей этой сложной картины лунного движения, Н.И. Идельсон говорит: «Еще более поразительно, что, как выяснилось через много столетий, динамическая теория Луны не нуждается ни в каких других равномерно нарастающих углах, кроме тех четырех, которые с таким дивным искусством вавилонская и греческая наука извлекла из наблюдений Луны» [54]. Эти четыре угла следующие: 1) среднее угловое расстояние Луны от Солнца (средняя элонгация⁴) D, суточное приращение n — n'=n(1-m); 2) среднее расстояние Луны от перигея (средняя аномалия) l; суточное приращение n — n₁=cn; 3) среднее расстояние Луны от восходящего узла F, приращение n — n₂=gn; 4) средняя аномалия Солнца (его среднее угловое расстояние от перигея солнечной орбиты) l', приращение n'=nm. Из общих теорем небесной механики вытекает, что необходимо и достаточно иметь здесь именно четыре независимых аргумента [54. С. 209, 477].

Гиппарх не разрабатывал теорий движений планет. Он лишь собрал наблюдения вавилонских астрономов и добавил к ним свои собственные. Все это явилось впоследствии материалом для планетной теории Птолемея.

Гиппарх ясно понимал, что прежние теории движений планет неудовлетворительны. А ведь такие теории существовали даже до Гиппарха, и по ним составлялись таблицы положений планет, примером которых служат «Вечные таблицы», на которые ссылается Птолемей в «Альмагесте» [17. С. 421]. Эти таблицы были основаны на больших циклах повторяемости положений планет как относительно Солнца, так и относительно звезд и собственных перигеев и апогеев. Подобные циклы подбирал и Гиппарх. Однако построение более или менее точной теории движения планет оказалось, как отмечает Птолемей, слишком трудной задачей даже для Гиппарха.

Исследования Гиппарха явились необходимым этапом для работ самого Птолемея. Вряд ли Птолемей сумел бы поставить и решить многие задачи, если бы перед ним не стоял пример Гиппарха.

Примечания

1 Как можно видеть из приведенных выше значений, изменяется не только долгота перигея Солнца, но и эксцентриситет его орбиты (на самом деле — земной орбиты). Эти явления получили физическое объяснение уже в рамках небесной механики, основанной на теории тяготения Ньютона.

2 Это несколько странное слово происходит от греческих слов аро — вдали и helios — Солнце; при их объединении в единое слово буква «о» выпадает и вместо apohelios пишут aphelios — афелий.

3 Слово «халдеи» происходит от ассирийского названия города Вавилона — Халду. Таким образом, халдеи — это вавилоняне. В современной исторической литературе термин «халдеи» не употребляется [78. С. 566-568].

4 Элонгацией в астрономии обычно называют угловое расстояние планеты или Луны от Солнца, хотя встречаются и другие значения этого термина (момент наибольшей элонгации нижней планеты, соответствующая конфигурация и др.).