В.А. Бронштэн

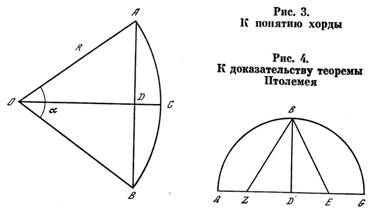
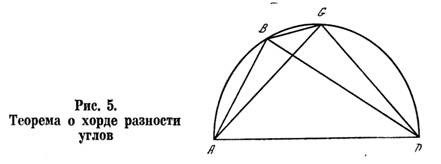
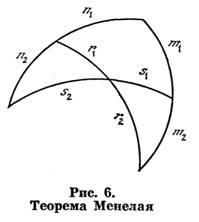
КЛАВДИЙ ПТОЛЕМЕЙ

* Предисловие * Глава 1 — Место и время действия * Глава 2 — Астрономия в Вавилоне и Греции до Гиппарха * Глава 3 — Астрономические исследования Гиппарха * Глава 4 — Краткое содержание «Альмагеста» * Глава 5 — Мировоззрение Птолемея * Глава 6 — Небесная сфера: расчеты и измерения * Глава 7 — Теория движения Солнца * Глава 8 — Теория движения Луны * Глава 9 — Звездный каталог * Глава 10 — Теория движения планет * Глава 11 — «Преступление Клавдия Птолемея» * Глава 12 — Работы Птолемея в области географии * Глава 13 — Работы Птолемея в области оптики * Глава 14 — Математика и музыка * Глава 15 — Птолемей и астрология * Глава 16 — Судьба «Альмагеста» * Глава 17 — От эпициклов Птолемея к законам Кеплера * Птолемеи и Коперник (послесловие редактора) * Литература *

Глава 6

Небесная сфера: расчеты и измерения

Установив, что небесный свод имеет форму сферы, Птолемей формулирует некоторые ее свойства и закономерности. Он вводит понятия полюсов мира, пебесного экватора и эклиптики. Далее он проводит через полюсы экватора и эклиптики еще один большой крут (колюр солнцестоянии), перпендикулярный к обоим. Точки пересечения эклиптики с экватором — это точки равноденствий, точки пересечения эклиптики с колюром солнцестояний — это точки солнцестояний.

Два основных движения небесной сферы — суточное и годичное. Первое увлекает все светила, второе — Солнце и планеты, но последние имеют еще свои, индивидуальные движения [17. С. 45].

Затем Птолемей вводит понятие о хорде угла. Хотя мы уже поясняли его в гл. 4, рассмотрим это понятие подробнее. Проведем дугу окружности (рис. 3) с центром в О и отложим некоторый центральный угол АОВ. Проведем затем хорду АВ. Введем шестидесятеричную систему счисления и примем радиус (АО=ОВ) равным 60 единицам. В этих же единицах будем считать и хорды.

Будем обозначать хорду угла α через chord α.

Нетрудно убедиться в том, что chord α=2Rsin(α/2),

где R — радиус окружности. Для доказательства проведем ОС — биссектрису угла α. Она пересечет хорду АВ в точке D. Поскольку Δ АОВ — равнобедренный, биссектриса является в нем также и медианой и высотой. Поэтому AD ┴ OD и AD = DB, В то же время AD/R=sin (α/2), откуда AB=2R sin (α/2). Справедливость формулы доказана.

Птолемей доказывает несколько теорем, которые позволяют ему составить таблицу хорд всех углов от 0 до 180°. Чтобы показать метод доказательств Птолемея, мы приведем здесь в качестве примера доказательство первой из этих теорем [17. С. 48—49].

«Имеем (рис. 4) полукруг ABG, описанный около центра D на диаметре ADG¹. Проведем DB┴AG в точке D. Разделим отрезок DG пополам в точке Е, проведем прямую ЕВ и отложим отрезок EZ = EB. Соединим Z с В прямой ZB.

Я утверждаю, что ZD есть сторона правильного десятиугольника, a BZ — сторона правильного пятиугольника.

Доказательство: Поскольку прямая DG делится в точке Е пополам, а прямая DZ есть ее продолжение²,

GZ * ZD + ED² = EZ²,

но

EZ² = BE²(EB = ZE)

и

EB² = ED² + DB²

откуда следует GZ * ZD + ED²=ED² + DB². Вычитая из обеих частей ED², получим

GZ * ZD = DB² = DG².

Таким образом, ZG разделено в крайнем и среднем отношении³ в точке D.

Но поскольку сторона шестиугольника и сторона десятиугольника, вписанных в ту же окружность, образуют крайнее и среднее отношения той же прямой линии и поскольку GD, будучи радиусом, представляет собой сторону правильного шестиугольника, DZ равна стороне правильного десятиугольника.

Аналогично, поскольку квадрат стороны пятиугольника равен сумме квадратов сторон шестиугольника и десятиугольника, если все они вписаны в ту же самую окружность, и в прямоугольном треугольнике BDZ квадрат BZ равен сумме квадратов ВТ), которая есть сторона шестиугольника и DZ, которая есть сторона десятиугольника, отсюда следует, что BZ равно стороне пятиугольника».

Таково доказательство Птолемея. Почти на каждом шагу он использует те или иные теоремы, доказательства которых содержатся в «Началах» Евклида, хотя и не делает ссылок, полагая, что этот классический труд известен читателям (приводимые здесь ссылки принадлежат одному из современных переводчиков «Альмагеста» Дж. Тумеру).

Как же использует Птолемей только что доказанную теорему? Обозначая символом р (от английского слова part — часть) те единицы, которыми пользуется Птолемей, найдем вместе с ним, что DE=30^P (DE — половина радиуса). DE²=900^P. BD=60^P. SD²=3600^P, EZ²=EB²=4500^P (EZ²=DE²+BD²), EZ=67;4,55^P, DZ=EZ-DE=37;4,55^P (о способе записи в шестидесятеричной системе мы говорили выше). Но DZ — сторона десятиугольника, которая стягивает нейтральный угол 36°. Значит, хорда угла 36° равна 37:4,55^P.

Аналогично Птолемей находит, что хорда центрального угла пятиугольника, т. е. 72°, равна 70;32,3^P; хорда центрального угла шестиугольника (60°) равна 60^P (радиусу); а поскольку квадраты хорд углов 90° и 120° равны соответственно двум и трем квадратам радиуса, Птолемей получает

chord 90° = (7200^P)^1/2 = 84;51,10^P

chord 120° = (10 800^P)^1/2 = 103;55,23^P.

Далее он использует известное свойство, что угол, опирающийся на диаметр, — прямой. Поэтому квадрат хорды

угла, дополняющего данный угол до 180°, равен квадрату диаметра минус квадрат хорды данного угла. Так он находит

chord 144° = 114;7,37^P, chord 108° = 97;4,55^P.

Имея хорды нескольких углов, Птолемей доказывает теорему, что хорда разности двух углов может быть найдена, если известны хорды этих двух углов. Для этого оп прежде доказывает другую теорему, которую можно сформулировать так: произведение диагоналей произвольного четырехугольника, вписанного в окружность, равно сумме произведений его противоположных сторон⁴. Иначе говоря, в четырехугольнике ABGD AG * BD = AB * DG + AD * BG. Эта теорема получила название теоремы Птолемея [17. С. 50-51].

Посмотрим теперь, как с помощью теоремы Птолемея доказывается теорема о хорде разности углов. Пусть нам даны хорды АВ и AG (рис. 5); AD — диаметр окружности.

Проведем хорду разности углов ADG и ADB — прямую BG. По теореме Птолемея, поскольку ABGD — вписанный в окружность четырехугольник,

АВ * GD + AD * BG = AG * BD

но AG * GD и AB * GD нам известны (AG и АВ заданы, BG и GD — хорды дополнительных углов), поэтому AD * BG находится путем вычитания. А так как AD = 120^P есть диаметр, то, поделив AD * BG на 120, мы получим хорду BG. Совершенно аналогично Птолемей доказывает далее теорему о хорде суммы углов с заданными хордами. Она тоже вычисляется без труда.

Теперь, составляя суммы и разности углов, хорды которых известны, можно найти хорды этих сумм и разностей, а затем использовать их, в свою очередь, для составления новых сумм и разностей, и т. д. Поскольку хорда 180° тоже известна и равна 120^P, мы можем так постепенно найти хорды всех углов, кратных углу 6°. А дальше Птолемей доказывает теорему о хорде половины угла. Теорема эта была когда-то доказана Архимедом, и хотя она является частным случаем теоремы о хорде разности углов, Птолемей приводит ее доказательство отдельно. Не повторяя его здесь, мы напишем лишь формулу хорды половины угла:

С помощью этой формулы Птолемей смог составить таблицу хорд всех углов от 0 до 180° через полтора градуса. Но он поставил себе задачей вычислить хорды углов через полградуса. А для этого надо было рассчитать хотя бы chord 0,5° или chord 1°, чтобы затем найти остальные по формулам сумм или разностей хорд.

Задача оказалась, как мы бы сказали теперь, аналитически неразрешимой. Найти хорду трети угла по хорде целого угла было невозможно. Это невозможно и в наши дни, если использовать методы только евклидовой геометрии⁵, подобно тому как неразрешима задача о трисекции угла (т. е. о разделении угла на три равные части с помощью только циркуля и линейки).

Птолемей нашел весьма остроумный выход из положения. Он применил одну из теорем Евклида о том, что отношение отрезков, отсекаемых прямой, проведенной из вершины треугольника, на противолежащей стороне, меньше отношения самих углов. По формуле хорды половины угла он вычислил chord (³/₄)° = 0;47,8^Р и chord (1¹/₂)° = 1;34,15^Р. Далее он составил отношения 1° : (³/₄)° = ⁴/₃ и (1¹/₂)° : 1° = ³/₂. На основании теоремы Евклида он утверждал, что

chord 1° < ⁴/₃ * 0;47,8^Р = l;2,50^Р,

chord 1° > ²/₃ * 1;34,15^Р = 1;2,50^Р.

Получив из этих двух соотношений одно и то же число для нижнего и верхнего предела chord 1°, Птолемей справедливо заключил, что chord 1°=1;2,50^Р. После этого для него не представляло никаких затруднений вычислить по формулам хорд сумм, разностей и половинных углов хорды всех остальных углов через полградуса [17. С. 57—60]. Никаких затруднений... Кроме колоссальной затраты времени. Ведь в распоряжении Птолемея не было никаких счетных машин или облегчавших вычисления таблиц. Неизвестно, были ли у него помощники, которым можно было поручить эти расчеты. Ради интереса автор взял на себя труд выполнить расчет хорды по формуле разностей, пользуясь методикой Птолемея, т. е. без всяких вычислительных средств, «на бумажке», как считают ученики начальной школы, причем в шестидесятеричной системе. Несмотря на известный опыт автора в такого рода вычислениях, один расчет занял у нас полчаса⁶. Можно полагать, что Птолемей был в таких расчетах опытнее автора и считал быстрее, но вряд ли он мог делать один расчет менее чем за 20 мин. Это значит, что расчет таблицы хорд (360 углов) занял у него около 120 ч напряженного труда.

Вернемся к методу, примененному Птолемеем для нахождения хорды угла в 1°. На первый взгляд кажется странным, что оба предела, верхний и нижний, дали одно и то же число. Но так получается, если ограничиться точностью, до которой считал Птолемей. Если сосчитать па один разряд шестидесятеричной системы точнее, то мы получим

(⁴/₃) chord (³/₄)° = 1;2,49,55,

(²/₃) chord (³/₂)° = 1;2,49,48.

Точное значение chord 1° = 1;2,49,54.

Линейное интерполирование между значениями верхнего и нижнего пределов (с учетом того, что угол 1° ближе к 0,75°, чем к 1,5°) дало бы: chord 1° = 1;2,49,53.

Есть указания, что таблица хорд, рассчитанная по формуле хорд половинных углов (без формул хорд сумм и разностей углов), была составлена еще Гиппархом. Но в столь полном виде, да еще с первыми разностями (приращениями хорды на один градус угла), она несомненно была вычислена Птолемеем впервые.

Из этого примера мы видим, каким усердным математиком и вычислителем был Птолемей. Стоит сравнить его в этом отношении с Иоганном Кеплером, которому в поисках истинной формы планетных орбит также приходилось по многу раз производить одни и те же вычисления, чтобы согласовать наблюдения Марса с теорией. Рассказывая в «Новой астрономии» о ходе своей работы по вычислениям (методом проб и ошибок) радиуса орбиты Марса, долготы его афелия и расстояний от центра круговой (тогда еще круговой!) орбиты Марса до Солнца и до центра экванта, Кеплер писал: «Если этот обременительный способ работы вам не нравится, вы можете справедливо пожалеть меня, поскольку я вынужден был проделать это по меньшей мере 70 раз с большой затратой времени». Сохранившиеся до нашего времени черновики расчетов Кеплера занимают 900 листов, исписанных мелким почерком [26,92].

В книге Птолемея мы не найдем подобных жалоб. Он спокойно и методично преподносит читателю окончательные результаты своих расчетов. А ведь в дальнейшем, при работе над теориями движения Луны и планет, ему приходилось делать вычисления куда более трудные, чем расчеты таблицы хорд. А главное, ему, как и впоследствии Кеплеру, нужно было согласовать свою теорию с наблюдениями, идти тем же методом проб и ошибок.

Об объеме математических вычислений и построений Птолемея говорит количество чертежей, иллюстрирующих его доказательства и выкладки: их в книге около двухсот. Кроме того, Птолемей приводит двадцать пять больших и малых таблиц, причем многие из них занимают по несколько страниц. В числе таблиц — звездный каталог, включающий положения 1025 звезд, таблицы солнечных и лунных затмений, движений планет, Луны, восходов и заходов светил и т. д.

Но вернемся к содержанию «Альмагеста». Покончив с определением и табулированием хорд (напоминаем, что хорды заменяют ему весь набор современных тригонометрических функций), Птолемей развивает основные положения и теоремы сферической тригонометрии. Важное место среди них занимают две теоремы Менелая о соотношениях хорд дуг четырех больших кругов, пересекающих друг друга, как показано на рис. 6. Птолемей доказывает, что эти дуги связаны соотношениями

chord 2m / chord 2m₁ = chord 2r / chord 2r₁ * chord 2s₂ / chord 2s,

chord 2r₂ / chord 2r₁ = chord 2m₂ / chord 2m₁ * chord 2n / chord 2n₂,

которые в переводе на современные обозначения имеют вид

sin 2m / sin 2m₁ = sin 2r / sin 2r₁ * sin 2s₂ / sin 2s,

sin 2r₂ / sin 2r₁ = sin 2m₂ / sin 2m₁ * sin 2n / sin 2n₂,

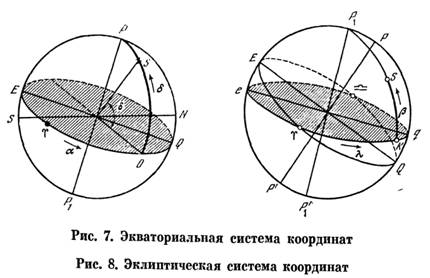
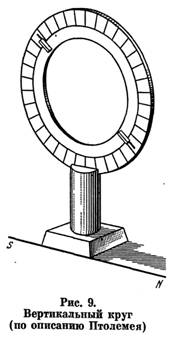
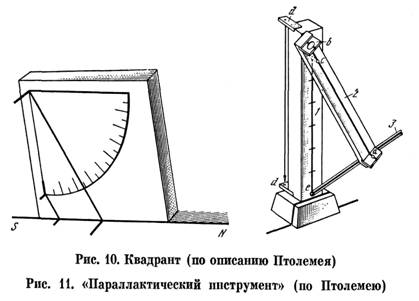
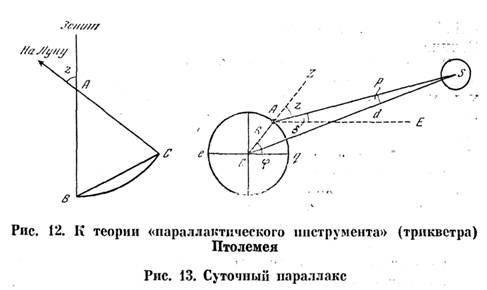
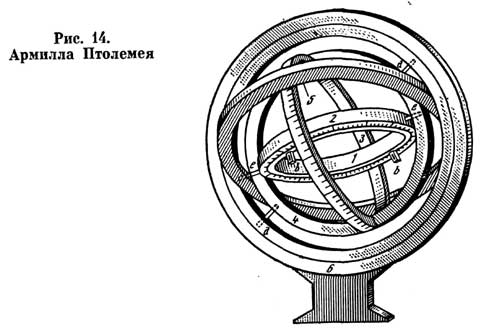
Здесь принято m = m1 + m2, n = n1 + n2, r = r1 + r2, s = s1 + s2.

Эти теоремы были впервые доказаны александрийским математиком и астрономом Менелаем, жившим и работавшим во второй половине I в. н. э. Птолемей и здесь не делает ссылки на приоритет Менелая (как не ссылается он на Евклида и Архимеда), хотя он не мог не читать его «Сферику», где изложены эти теоремы⁷. В дальнейшем он упоминает лишь о наблюдениях Менелая.

Далее Птолемей вводит понятия sphaera recta (прямая сфера) и sphaera obliqua (наклонная сфера), которыми он в дальнейшем неоднократно пользуется [17. С. 71—75]. Под «прямой сферой» он понимает такое положение небесной сферы, когда небесный экватор перпендикулярен горизонту (мы знаем, что такое расположение обоих больших кругов наблюдается на экваторе). Под «наклонной сферой» Птолемей понимает любое другое положение небесной сферы, когда экватор наклонен к горизонту под острым углом.

Для нас эти термины звучат немного странно, но ведь именно от «прямой сферы» берет начало всем известный термин прямое восхождение (одна из двух сферических координат в экваториальной системе). В самом деле, если наблюдатель расположен па экваторе, разность времен восхода светила и точки весеннего равноденствия, переведенная в единицы дуги (помня, что 1 ч соответствует дуге в 15°), как раз и будет прямым восхождением светила. Если точка весеннего равноденствия находится на горизонте, то дуга, которую прошло светило с момента его восхода, также будет равна прямому восхождению.

Следующей задачей, которую решает Птолемей, является вычисление «таблицы наклонений», как она названа кем-то из переписчиков или переводчиков «Альмагеста», а точнее, склонений точек на эклиптике в функции дуг самой эклиптики (т. е. небесных долгот), отсчитываемых от точки весеннего равноденствия через градус [17, С. 72]. Именно для этого расчета Птолемею и была нужна первая теорема Менелая.

В наше время расчет склонений центра диска Солнца (который движется по эклиптике) или интересующих нас точек на эклиптике делается без громоздкой теоремы Менелая, с помощью формул сферического треугольника, образованного дугами эклиптики, экватора и круга склонения данной точки. Птолемей не мог решать сферический треугольник современным способом не только из-за отсутствия в то время понятия косинуса, столь же нужного в формулах сферической тригонометрии, как и синус (последний можно было заменить хордой двойного угла), но и потому, что в эти формулы входят функции двугранных углов (например, между плоскостями экватора и эклиптики), а Птолемей мог иметь дело только с дугами. И хотя он использует угол наклона эклиптики к экватору, но, в сущности говоря, он оперирует не с двугранным углом, а с дугой колюра солнцестояний, равной наибольшему расстоянию эклиптики от экватора. Этот угол, как мы помним, Птолемей принял равным 23° 51'20".

От склонений Птолемей переходит к расчету прямых восхождений точек эклиптики, выбранных через 10° по долготе. На двух примерах он показывает, в каком порядке следует вести вычисления, после чего дает небольшую табличку прямых восхождений девяти точек эклиптики. Собственно, Птолемеи приводит не прямые восхождения, а проекции на экватор десятиградусных и тридцатиградусных дуг эклиптики — от точки весеннего равноденствия до точки летнего солнцестояния (т. е. в интервале долгот 0—90°). Но получить отсюда прямые восхождения не составляет труда —это простая арифметика. Равным образом нетрудно распространить расчет на всю эклиптику: ввиду симметричного расположения обоих кругов, те же десятиградусные дуги будут фигурировать и в остальных трех квадрантах эклиптики, что подчеркивает, заключая I книгу, Птолемей [17. С. 74].

Обратим внимание читателя на то, с какой дотошностью подходит Птолемей к изложению своих математических методов. Его доказательства теорем безукоризненны с точки зрения математической логики и в то же время просты и понятны. Свои построения он поясняет чертежами. Так и кажется, что он писал свою книгу в расчете не на таких же маститых астрономов, как он сам, а на студентов. И действительно, «Альмагест» в течение полутора тысяч лет был стандартным учебником астрономии: по нему учились будущие ученые и студенты в первых европейских университетах.

В этой связи интересно напомнить, что автор одного из лучших переводов «Альмагеста» К. Манициус⁸, выпуская это сочинение в Лейпциге в 1912 г. на немецком языке, назвал его «Handbuch der Astronomie», что буквально означало «Справочник по астрономии» или «Руководство по астрономии». Конечно, «Альмагест» был скорее руководством, чем справочником. Но когда спустя полвека этот перевод был переиздан в ГДР (в том же Лейпциге) под редакцией и с примечаниями крупнейшего специалиста по истории античной науки О. Нейгебауэра [14] и поступил в продажу в Москве в магазине «Дружба», на карточке в картотеке наличия было написано «Справочник по астрономии». Полагая, что в ГДР выпущен новый современный справочник по астрономии, автор попросил показать ему книгу. Велико же было его удивление, когда выяснилось, что под этим вполне современным названием продается древний «Альмагест» Птолемея! Автор пытался убедить работников магазина «Дружба», что на карточке надо написать: «К. Птолемей. "Альмагест"», что это вовсе не справочник по астрономии, а классический труд, написанный восемнадцать веков назад и известный именно под этим названием, но все было напрасно. «„Handbuch" по-немецки означает „справочник", и мы обязаны название книги переводить на русский язык точно», — отвечали мне работники магазина. Вносить исправления в картотеку они отказались.

Во второй книге своего труда Птолемей ставит и решает ряд задач, как бы мы выразились теперь, практической астрономии. Прежде всего он уточняет, что «наша часть обитаемого мира» находится в северном полушарии и занимает по долготе менее 180°. Неясно, какими данными располагал Птолемей для последнего вывода. Долготы были известны далеко не для всех стран, о которых мог знать Птолемей. Так, он знал о существовании Британии далеко на западе и, несомненно, Индии и Китая на востоке (о них должны были рассказывать ему александрийские и иностранные купцы). Но достоверное определение разности долгот он имел лишь одно: лунное затмение—330 сентября 20 наблюдалось одновременно в Карфагене (долгота ок. 10°) и в Арбеле, на реке Тигр (долгота ок. 46°). Об этом факте сообщается в «Географии» Птолемея [116], Тем не менее он был прав в своих представлениях о расположении «нашей части обитаемого мира».

После этого введения Птолемей ставит и решает следующие практические задачи [17. С. 75—76]:

1) определить угловое расстояние полюса от горизонта или (равное ему) зенитное расстояние небесного экватора, измеряемое вдоль небесного меридиана;

2) для тех мест, где Солнце достигает зенита, определить, когда и как часто это происходит;

3) определить отношения полуденных теней от гномона в дни равноденствий и солнцестояний;

4) определить разность между длительностью самого длинного и самого короткого дня и длиной дня во время равноденствий;

5) определить приращение и убывание длительности дней и ночей в разные времена года;

6) определить дуги экватора, которые восходят и заходят одновременно с заданными дугами эклиптики (эта задача нужна для вычисления так называемых гелиакических восходов и заходов);

7) определить величины углов между эклиптикой и

наиболее важными большими кругами: небесным меридианом, горизонтом и кругом высоты (большим кругом, проходящим через зенит и надир).

Методика решения этих задач Птолемеем нам уже известна по примерам, рассмотренным выше. Результаты своих расчетов Птолемей приводит в виде таблиц.

Представляет интерес описание Птолемеем 39 широтных поясов, которые он выбирает по аргументу наибольшей длительности дня в день летнего солнцестояния [17. С. 82—90]. Сначала он выбирает те широты, где длительность дня нарастает с интервалом в ¹/₄ ч. Поэтому после экватора (день 12 ч) он берет широту 4° 15', где наибольшая длительность дня 12¹/₄ ч. Девятая по счету параллель соответствует широте 30° 22' (что недалеко от Александрии), где наибольшая длительность дня достигает 14 ч, одиннадцатая — проходит через остров Родос, где наблюдал Гиппарх. В описаниях этих параллелей мы находим целый ряд хорошо нам знакомых рек, морей, озер, в том числе и находящихся теперь на территории нашей страны. Так, перед нами проходят реки Дунай (тогда Истр), Днепр (Борисфен), Дон (Танаис), Азовское море (озеро Меотида), Черное море (Понт Евксинский). Из других мест, представляющих интерес, Птолемей называет город Массилию (нынешний Марсель), Британские острова, и даже Гебридские и Шетландские острова. Но о географических исследованиях Птолемея мы поговорим ниже, в гл. 12. В своем описании параллелей Птолемей приводит для каждой из них астрономические характеристики. Кроме наибольшей длительности дня, он указывает наибольшую высоту Солнца в полдень (или факт прохождения Солнца через зенит), длину тени гномона в это время и ряд других характеристик. Он правильно определяет свойства тропиков и полярных кругов, условия видимости светил на Северном полюсе.

Однако Птолемей не только доказывал теоремы и производил вычисления, он еще и вел наблюдения. Это были в основном позиционные наблюдения, сводившиеся к определению астрономических координат небесных светил.

Птолемей использует две системы астрономических координат, применяемые и в наше время: экваториальную и эклиптическую. В экваториальной системе (рис. 7) первая координата — уже известное нам прямое восхождение α, отсчитываемое по дуге экватора EQ от точки весеннего равноденствия Y до основания D круга склонения светила, т. е. большого круга, проведенного через оба полюса небесной сферы (полюсы мира) РР₁ и светило S. Вторая координата — склонение δ — отсчитывается от небесного экватора D до светила S по кругу склонения PD. Эти координаты в принципе построены так же, как и географические долгота и шпрота, причем в обеих системах есть и полюсы, и экватор, и параллели (параллели небесных светил называют суточными параллелями, поскольку светило описывает свою параллель в течение суток). Вот только вместо географических меридианов, сходящихся у полюсов Земли, в экваториальной системе фигурируют круги склонения, также сходящиеся в полюсах мира.

Совершенно аналогично построена эклиптическая система координат, только в ней основная плоскость — плоскость эклиптики, основной большой круг — эклиптика eq. У нее также есть два полюса, северный Р₁ и южный Р₁', располагавшиеся, как считал Птолемей, на расстоянии 23°51'20" от соответствующих полюсов мира (мы уже указывали на на ошибку, допущенную Птолемеем в оценке этого угла). Первая координата — долгота λ — отсчитывается вдоль эклиптики от точки весеннего равноденствия Y против часовой стрелки до основания круга широты светила К, Вторая координата — широта β — отсчитывается по кругу широты KР₁ от эклиптики до светила S (рис. 8). Эклиптические долготу и широту не надо путать с одноименными географическими координатами.

Трудность определения астрономических координат из наблюдений состоит в том, что ни точка весеннего равноденствия (начало отсчета прямого восхождения и долготы), ни экватор, ни эклиптика ничем на небе не обозначены. Как выходил из этого затруднения Птолемей (а до него Гиппарх), мы скоро узнаем.

Птолемей дает уже в конце первой книги описание одного из своих приборов [17. С. 61—62]. Правда, он не изобразил ни одного из них хотя бы схематически, но по его подробным описаниям это сделали исследователи его трудов.

Схемы приборов Птолемея, воспроизводимые в этой книге, заимствованы у них.

Для измерения дуг в вертикальной плоскости Птолемей использовал следующий прибор (рис. 9). На прочном вертикальном столбе укреплено также в вертикальной плоскости бронзовое кольцо, разделенное на градусы и доли градуса. Внутри этого кольца и в одной с ним плоскости поворачивается другое кольцо — с двумя стрелками-указателями, лежащими точно на 180° одна от другой на одной прямой. Бронзовое кольцо устанавливается строго вертикально (что проверяется отвесом) и в плоскости небесного меридиана. Как именно осуществляется установка этого инструмента в плоскости меридиана, Птолемей не сообщает, предполагая, что эта плоскость каким-то путем проложена заранее. Как сообщает О. Нейгебауэр [116. Т. 2. С. 841], остроумный способ прокладки направления меридиана предложил Диодор Александрийский (I в. до н. э.) в недошедшем до нас сочинении «Аналемма». Плоскость меридиана устанавливалась по трем положениям тени гномона. Несомненно, этот метод был известен Птолемею, хотя возможно, что он использовал и какой-либо другой метод, например метод равных высот. Этот метод основан на том, что высоты светила в точках, симметричных относительно небесного меридиана, равны. Но тогда и длина тени гномона в моменты, когда Солнце находится в таких точках, будет одинакова. Поэтому достаточно начертить на горизонтальной площадке, где стоит гномон, несколько концентрических дуг с северной стороны, центром которых будет основание гномона, и отмечать положения кончика тени, когда он будет касаться этих окружностей. Если затем провести биссектрисы углов АОВ, COD и т. д. (теоретически они должны совпасть), то мы получим направление полуденной линии, а тем самым и положение плоскости небесного меридиана.

Помимо описанного выше прибора, явившегося прообразом целой серии инструментов, известных под названием меридианного круга и используемых в наши дни для наблюдений прохождений звезд и других светил через меридиан, Птолемей приводит конструкцию другого, более простого прибора [17. С. 62—63]. Он представляет собой прочную доску из камня или дерева с гладко отполированной боковой стороной (рис. 10). Доска устанавливается вертикально в плоскости небесного меридиана. На ней из некоторой точки вблизи верхнего южного угла проводятся вертикальная и горизонтальная прямые и стягивающая их дуга в 90°. Эта дуга делится на градусы и их доли. К центру дуги крепится линейка, которая может поворачиваться вокруг него. На линейке перпендикулярно доске укрепляются два небольших цилиндрических шпенька, из которых верхний должен проходить через центр дуги. Когда Солнце проходит через меридиан, линейка устанавливается так, чтобы тень верхнего шпенька падала точно на нижний. Тогда деление на дуге квадранта покажет нам высоту Солнца.

Этот прибор послужил прообразом для измерительных приборов, названных квадрантами и использовавшихся в XV—XVI вв. такими наблюдателями, как Улугбек и Тихо Браге. Ради повышения точности измерений им придавали довольно большие размеры (десятки метров). Шпеньки Птолемея были заменены диоптрами.

С помощью этих двух приборов Птолемей наблюдал высоту Солнца в меридиане в дни равноденствий и солнцестояний и из этих наблюдений вывел угол наклона эклиптики к экватору, близкий к значениям, полученным ранее Эратосфеном и Гиппархом (см. с. 25).

В пятой книге (гл. 12) Птолемей описывает третий угломерный прибор, названный им параллактическим инструментом. Такое название Птолемей дал этому прибору потому, что он использовал его для определения параллакса Луны [17. С. 244-247].

К установленному вертикально (с помощью отвеса dd) деревянному столбу прямоугольного сечения 1 (рис. 11) на шарнире крепится линейка 2 с укрепленными в ее верхнем и нижнем концах диоптрами (визирами). Отверстие нижнего диоптра а (в которое смотрит наблюдатель) небольшое, у верхнего b — побольше, чтобы в него была видна вся Луна. Посередине столба 1 сверху вниз проведена прямая с делениями, начинающимися от шарнира с. Она разделена на 60 частей и их доли. Такая же прямая длиной 60 частей проведена и на поворачивающейся линейке 2. Линейка 2 укреплена на шарнире с так, чтобы она не опускалась от собственного веса, но чтобы ее мог повернуть наблюдатель. Она вращается в плоскости меридиана.

В нижней части столба на другом шарнире е укреплена еще одна планка 5, которая имеет также подвижное соединение с линейкой 2 и при ее повороте тоже поворачивается. Она также имеет деления, равные по длине делениям на столбе 1 и на линейке 2.

Наблюдатель наводит линейку с диоптрами на Луну, когда она проходит через меридиан, и закрепляет ее. Поскольку в треугольнике ABC (рис. 12) стороны АВ к АС равны (и содержат по 60 делений каждая), сторона ВС равна хорде угла z = BAC, т. е. зенитному расстоянию Луны, в тех же единицах. Вертикальное положение столба проверяется с помощью отвеса.

Почему же этот прибор назван параллактическим?

Ведь с его помощью определяется лишь зенитное расстояние Луны. Напомним, что суточным параллаксом (рис. 13) называется угол, под которым в данный момент из светила виден радиус Земли, на конце которого находится наблюдатель. Если светило в зените, то параллакс равен нулю, если на горизонте, параллакс достигает своего максимального значения (горизонтальный параллакс). Вообще же параллакс р(угла ASC) равен

sin p = (R/d) sin z,

где R — радиус Земли, d — расстояние от центра Земли до светила, z — его зенитное расстояние.

Казалось бы, в этой задаче два .неизвестных d и р при одном уравнении. Но из рис. 13 видно, что явление параллакса увеличивает зенитное расстояние светила на величину самого параллакса. А поскольку Птолемей, зная склонение Луны δ = углу EAS, мог вычислять ее зенитные расстояния на моменты наблюдений, не искаженные параллаксом, разность наблюденных и вычисленных значений z сразу давала ему р, а по приведенной выше формуле (с заменой синуса на хорду двойного угла) он мог определить и расстояние до Луны d в долях радиуса Земли.

Поскольку Луна может иногда достигать склонения δ = +29°, на широте Александрии (φ = +31°) она проходит в это время всего лишь в 2° от зенита. Для этого нужно, однако, чтобы Луна была одновременно близ точки летнего солнцестояния и в 90° к востоку от восходящего узла своей орбиты. Поскольку линия узлов лунной орбиты совершает полный оборот относительно точки весеннего равноденствия за 18²/₃ года, сочетание обоих условий повторяется именно с этим периодом.

Птолемей утверждает, что он наблюдал Луну в таком положении, но не сообщает даты наблюдения [17. С. 246—247]. Поскольку, однако, известно, что 1 октября 135 г. Птолемей наблюдал Луну в 5° к северу от точки зимнего солнцестояния, линия узлов должна была сделать пол-оборота, чтобы реализовалось положение, описанное выше (Луна на 5° севернее точки летнего солнцестояния). Это значит, что Птолемей мог наблюдать Луну в этом положении либо в июне—июле 126 г., либо в начале января 145 г. [131. С. 247]. Обе даты выходят за пределы периода, когда Птолемей проводил астрономические наблюдения, упоминаемые в его книге (26 марта 127 г. — 2 февраля 141 г.). Конечно, нет ничего невозможного в том, что Птолемей начал наблюдать на 9 месяцев раньше, чем это зафиксировано сообщаемыми им датами наблюдений, или провел дополнительное наблюдение Луны в 145 г. Возможно также, что наблюдение Луны в 126 г. провел и передал Птолемею упоминаемый им не раз математик Теон.

Параллактический прибор Птолемея, получивший впоследствии название трикветр, применялся многими астрономами после него. Его описание и чертеж мы находим в классическом труде Коперника «О вращениях...», а также в «Механике обновленной астрономии» Тихо Браге. Именно он изображен на знаменитой картине польского художника Яна Матейки «Коперник» (1873 г.). Интересно, что подлинный трикветр Коперника спустя 40 лет после его смерти попал в руки Тихо Браге и был им подробно описан в вышеупомянутой книге, вышедшей в 1598 г. [124].

Последний и самый сложный прибор, описанный Птолемеем в той же пятой книге «Альмагеста» это — армиллярная сфера с диоптрами для наблюдения. Впрочем, Птолемей называет свой прибор астролябией (αστρολαβον), что буквально означает «для определения положений светил». Этот прибор стал «моделирующим» для астролябий, получивших распространение на арабском Востоке в IX—XIII вв., изображавших небесную сферу в стереографической проекции (введенной Птолемеем в «Планисферии»). Армиллярной сферой Птолемей называл другой (демонстрационный) прибор.

Вот как устроен первый прибор (рис. 14). Основой его является описанный нами ранее меридианный круг (см. рис. 9). Но в диаметрально противоположных точках, отмеченных на рисунке буквами dd, меридианного кольца 6, соответствующих положениям полюсов мира на данной широте⁹, просверлены отверстия и в них укреплены два штифта, вокруг которых может поворачиваться кольцо 4, изображающее колюр солнцестояний. На расстоянии от точек dd, измеряемом углом наклона эклиптики к экватору или равной ему дугой между полюсами мира и эклиптики, через кольцо 4 пропущены

два других штифта ее, образующих ось, вокруг которой могут поворачиваться: с внутренней стороны кольцо 2, разделенное на градусы и их доли, а с наружной стороны кольцо 5. С кольцом 4 жестко скреплено перпендикулярно ему кольцо 5, изображающее эклиптику и также разделенное по наружной (внешней) поверхности на градусы и их доли. Внутри кольца 2, в одной с ним плоскости, укреплено кольцо 1 с двумя диаметрально противоположными диоптрами bb, служащими для наблюдений [17. С. 217-219].

С помощью этого прибора светило можно наблюдать не только в меридиане, но в любом положении на небе. По идее Птолемея после наведения диоптров bb на светило можно было по делениям круга 2 отсчитать его долготу, а по делениям круга 4 (отсчитываемым с помощью круга 5, который для этого должен быть установлен в одной плоскости с кругом 2) — широту.

Однако наблюдения с этим прибором требовали известного навыка со стороны наблюдателя. В отличие от современных астрономических приборов, в которых наведение на светило осуществляется поворотом трубы прибора вокруг двух взаимно перпендикулярных осей, в астролябии Птолемея нужно было поворачивать подвижные части прибора вокруг трех осей: вокруг полярной оси dd, вокруг оси эклиптики ее и вокруг оси колец 1 и 2, лежащей в плоскости эклиптики (по аналогии с осью склонений современных телескопов-экваториалов ее можно назвать осью широт).

Впоследствии, в 1581 г., искусный наблюдатель Тихо Браге воспроизвел по описанию Птолемея его прибор, назвав его «зодиакальными армиллами» (слово «армилла» означает «кольцо»; Тихо Браге употреблял это слово во множественном числе). Видимо, этот прибор не удовлетворил Тихо Браге, и спустя три года он заменил его «экваториальными армиллами», где, кроме меридиана, имеются лишь два кольца: небесный экватор и круг склонения, а поворот осуществляется вокруг двух взаимно перпендикулярных осей: полярной и оси склонений [27].

С помощью описанных здесь приборов Птолемей и производил все свои наблюдения положений небесных светил. Естественно, все они велись невооруженным глазом. Их точность зависела от точности наведения шпеньков или диоптров, от правильности установки самого инструмента, наконец, от точности делений и их правильного считывания (большинство наблюдений проводилось ночью). Точность наблюдений Птолемея не превышала 10 мин дуги. Еще ниже была точность наблюдений, связанных с регистрацией времени (моменты затмений, покрытий звезд Луной, прохождений светил через меридиан). Точных часов в те времена не было, а существовавшие солнечные, песочные и водяные часы давали точность не выше 15 мин времени, что в переводе на единицы угла могло привести к ошибкам в определении прямых восхождений и эклиптикальных долгот в 3-4°.

Примечания

1 Разумеется, Птолемей обозначал точки на схемах греческими буквами, в алфавитном порядке. Этим объясняется выбор букв. В английском переводе Тумера и в нашем тексте греческие буквы заменены латинскими: А, В, G, D, Е, Z и соответствуют прописным греческим буквам А, В, Г, Δ, Е, Z.

2 Нижеследующее равенство доказывается у Евклида («Начала», II, 6) [99]. Поскольку GZ*ZD=(EZ+EG)*ZD=(EZ+ED)*(EZ-ED)=EZ²-ED², GZ*ZD+ED²=EZ².

3 Евклид («Начала», VI, определение 3): «Прямая разделяется в крайнем и среднем отношении, если отношение всей прямой к большему ее отрезку равно отношению большего отрезка к меньшему» [99].

4 Для ясности мы здесь (и далее) приводим все теоремы и доказательства в современных формулировках. Птолемей вместо «произведение отрезков» писал «прямоугольник, построенный на отрезках», имея в виду его площадь. Очевидно, что обе формулировки равносильны.

5 Задача может быть разрешена с использованием кубических уравнений, не известных Птолемею.

6 Любопытно, что такой же расчет на микрокалькуляторе «Электроника БЗ-36» занимает в десятичной системе 7-8 с, в шестидесятеричной — 25 с.

7 Сочинение Менелая «Сферика» в обработке хорезмийского ученого X-XI вв. Ибн Ирака (учителя Бируни) дошло до нас и в 1936 г. было издано М. Краузе [109] на арабском языке и в немецком переводе.

8 Манициус Карл Генрих (1848-1922) — профессор высшей школы в Дрездене, специалист по древним языкам и истории науки, автор переводов на немецкий язык сочинений Гиппарха, Гемина, Птолемея, Прокла, «Малого астронома».

9 Напомним читателям, что угловая высота полюса мира над горизонтом равна широте места.